Estado de esfuerzos.pdf
- 1. Contenidos 1 Estado de Esfuerzos Planos Esfuerzos en Planos Oblicuos Esfuerzos Principales Cı́rculo de Mohr Problemas Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 2 / 30
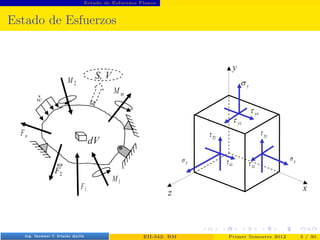
- 2. Estado de Esfuerzos Planos Estado de Esfuerzos Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 3 / 30
- 3. Estado de Esfuerzos Planos Estado de Esfuerzos Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 3 / 30
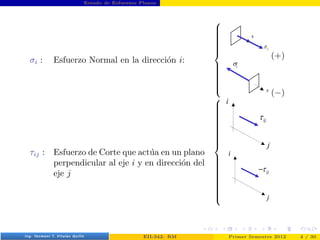
- 4. Estado de Esfuerzos Planos σi : Esfuerzo Normal en la dirección i: (+) (−) τij : Esfuerzo de Corte que actúa en un plano perpendicular al eje i y en dirección del eje j Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 4 / 30
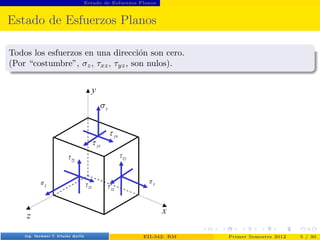
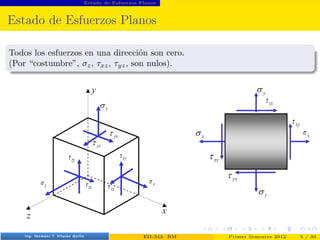
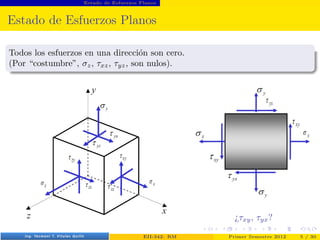
- 5. Estado de Esfuerzos Planos Estado de Esfuerzos Planos Todos los esfuerzos en una dirección son cero. (Por “costumbre”, σz, τxz, τyz, son nulos). Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 5 / 30
- 6. Estado de Esfuerzos Planos Estado de Esfuerzos Planos Todos los esfuerzos en una dirección son cero. (Por “costumbre”, σz, τxz, τyz, son nulos). Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 5 / 30
- 7. Estado de Esfuerzos Planos Estado de Esfuerzos Planos Todos los esfuerzos en una dirección son cero. (Por “costumbre”, σz, τxz, τyz, son nulos). ¿τxy, τyx? Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 5 / 30
- 8. Estado de Esfuerzos Planos ¿τxy, τyx? P Mz = 0 txydydz(dx) − tyxdxdz(dy) = 0 τxy = τyx Generalizando: τxz = τzx τyz = τzy Los esfuerzos cortantes sobre dos planos ortogona- les que pasan por un mismo punto, son iguales en magnitud y de sentido contrario. Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 6 / 30
- 9. Estado de Esfuerzos Planos Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 7 / 30
- 10. Estado de Esfuerzos Planos Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 8 / 30
- 11. Estado de Esfuerzos Planos Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 9 / 30
- 12. Estado de Esfuerzos Planos Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 10 / 30
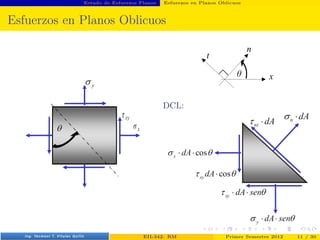
- 13. Estado de Esfuerzos Planos Esfuerzos en Planos Oblicuos Esfuerzos en Planos Oblicuos Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 11 / 30
- 14. Estado de Esfuerzos Planos Esfuerzos en Planos Oblicuos Esfuerzos en Planos Oblicuos DCL: Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 11 / 30
- 15. Estado de Esfuerzos Planos Esfuerzos en Planos Oblicuos X Fn = 0 Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 12 / 30
- 16. Estado de Esfuerzos Planos Esfuerzos en Planos Oblicuos X Fn = 0 σn · A − σx · A · cos(θ) · (cos(θ)) − τxy · A · cos(θ) · (sen(θ)) − σy · A · sen(θ) · (sen(θ)) − τxy · A sen(θ) · (cos(θ)) = 0 Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 12 / 30
- 17. Estado de Esfuerzos Planos Esfuerzos en Planos Oblicuos X Fn = 0 σn · A − σx · A · cos(θ) · (cos(θ)) − τxy · A · cos(θ) · (sen(θ)) − σy · A · sen(θ) · (sen(θ)) − τxy · A sen(θ) · (cos(θ)) = 0 σn = σx · cos2 (θ) · +σy · sen2 (θ) + 2 · τxy · sen(θ) · cos(θ) σn = σx · 1 + cos(2θ) 2 + σy · 1 − cos(2θ) 2 + τxy · sen(2θ) Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 12 / 30
- 18. Estado de Esfuerzos Planos Esfuerzos en Planos Oblicuos X Fn = 0 σn · A − σx · A · cos(θ) · (cos(θ)) − τxy · A · cos(θ) · (sen(θ)) − σy · A · sen(θ) · (sen(θ)) − τxy · A sen(θ) · (cos(θ)) = 0 σn = σx · cos2 (θ) · +σy · sen2 (θ) + 2 · τxy · sen(θ) · cos(θ) σn = σx · 1 + cos(2θ) 2 + σy · 1 − cos(2θ) 2 + τxy · sen(2θ) σn = σx + σy 2 + σx − σy 2 · cos(2θ) + τxy · sen(2θ) Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 12 / 30
- 19. Estado de Esfuerzos Planos Esfuerzos en Planos Oblicuos X Ft = 0 τnt · A − σx · A · cos(θ) · (sen(θ)) − τxy · A · cos(θ) · (cos(θ)) − σy · A · sen(θ) · (cos(θ)) − τxy · A · sen(θ) · (sen(θ)) = 0 τnt = σy · sen(θ) · cos(θ) − σx · A · cos(θ) · sen(θ) + τ2 xy · cos2 (θ) − τ2 xy · sen2 (θ) τnt = − 1 2 · (σx − σy) · sen(2θ) + τxy · cos(2θ) Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 13 / 30
- 20. Estado de Esfuerzos Planos Esfuerzos en Planos Oblicuos Importante La normal al plano forma un ángulo θ con el eje x. Las ecuaciones fueron deducidas con signos positivos. Luego, al emplearse deben reemplazarse las magnitudes y signos que correspondan. Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 14 / 30
- 21. Estado de Esfuerzos Planos Esfuerzos Principales Esfuerzos Principales Dado que σn = σn(θ) y τnt = τnt(θ), existen ciertos valores de θ tal que dichas funciones sean un máximo o un mı́nimo. (σn máx, σn mı́n) Esfuerzos principales (σp) Planos (σn máx, σn mı́n) Planos principales (θp) σn es mı́nimo para: σnθ = −(σx − σy) · sen(2θ) + 2 · τxy · cos(2θ) = 0 Recordar: τnt = −1 2 · (σx − σy) · sen(2θ) + τxy · cos(2θ) tg(2θp) = τxy 1 2 (σx − σy) Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 15 / 30
- 22. Estado de Esfuerzos Planos Esfuerzos Principales tg(2θp) = τxy 1 2 (σx − σy) Existen 2 valores de 2θp, desfasados 180◦ . Existen 2 valores de θp separados 90◦ . θp1 y θp2 definen el plano de máximo o mı́nimo esfuerzo normal. Notar que σnθ = 2 · τnt = 0. En Planos Principales τnt es nulo tg(2θp) = τxy 1 2 (σx − σy) Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 16 / 30
- 23. Estado de Esfuerzos Planos Esfuerzos Principales cos(2θp) = 1 2 (σx − σy) s 1 2 (σx − σy) 2 + τ2 xy sen(2θp) = τxy s 1 2 (σx − σy) 2 + τ2 xy σn = σx + σy 2 + σx − σy 2 · cos(2θ) + τxy · sen(2θ) σp1,p2 = 1 2 · (σx + σy) ± s 1 2 (σx − σy) 2 + τ2 xy Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 17 / 30
- 24. Estado de Esfuerzos Planos Esfuerzos Principales d2 σn dθ2 Puntos de Inflexión, Planos de máximo o mı́ni- mo Esfuerzo Normal d2 σn dθ2 = (−) θp1 define el Plano de Máximo Esfuerzo Normal d2 σn dθ2 = (+) θp2 define el Plano de Mı́nimo Esfuerzo Normal d2 σn dθ2 = −2 · (σx − σy) · cos(2θ) − 4 · τxy · sen(2θ) Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 18 / 30
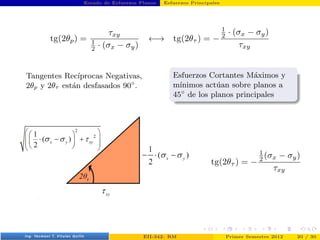
- 25. Estado de Esfuerzos Planos Esfuerzos Principales En forma analoga, τnt es máximo o mı́nimo para: τntθ = −(σx − σy) · cos(2θ) − 2 · τxy · sen(2θ) = 0 tg(2θτ ) = − 1 2 · (σx − σy) τxy tg(2θp) = τxy 1 2 · (σx − σy) ←→ tg(2θτ ) = − 1 2 · (σx − σy) τxy Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 19 / 30
- 26. Estado de Esfuerzos Planos Esfuerzos Principales tg(2θp) = τxy 1 2 · (σx − σy) ←→ tg(2θτ ) = − 1 2 · (σx − σy) τxy Tangentes Recı́procas Negativas, 2θp y 2θτ están desfasados 90◦ . Esfuerzos Cortantes Máximos y mı́nimos actúan sobre planos a 45◦ de los planos principales tg(2θτ ) = − 1 2 (σx − σy) τxy Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 20 / 30
- 27. Estado de Esfuerzos Planos Esfuerzos Principales sen(2θp) = − 1 2 (σx − σy) s 1 2 (σx − σy) 2 + τ2 xy cos(2θp) = τxy s 1 2 (σx − σy) 2 + τ2 xy τnt = − 1 2 · (σx − σy) · sen(2θ) + τxy · cos(2θ) τmáx,mı́n = ± s 1 2 (σx − σy) 2 + τ2 xy Recordar θp1,p2 Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 21 / 30
- 28. Estado de Esfuerzos Planos Esfuerzos Principales d2 τnt dθ2 Puntos de Inflexión, Planos de máximo o mı́ni- mo Esfuerzo Cortante d2 τnt dθ2 = (−) θτ define el Plano de Máximo Esfuerzo Cortante d2 τnt dθ2 = (+) θτ define el Plano de Mı́nimo Esfuerzo Cortante d2 τnt dθ2 = 2 · (σx − σy) · sen(2θ) − 4 · τxy · cos(2θ) Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 22 / 30
- 29. Estado de Esfuerzos Planos Cı́rculo de Mohr Cı́rculo de Mohr Representación gráfica de las ecuaciones desarrolladas para σn y τnt. σn − 1 2 (σx + σy) = 1 2 (σx − σy) · cos(2θ) + τxy · sen(2θ) τnt = − 1 2 · (σx − σy) · sen(2θ) + τxy · cos(2θ) Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 23 / 30
- 30. Estado de Esfuerzos Planos Cı́rculo de Mohr Cı́rculo de Mohr Representación gráfica de las ecuaciones desarrolladas para σn y τnt. σn − 1 2 (σx + σy) = 1 2 (σx − σy) · cos(2θ) + τxy · sen(2θ) τnt = − 1 2 · (σx − σy) · sen(2θ) + τxy · cos(2θ) σn − 1 2 (σx + σy) 2 + τ2 nt = 1 2 (σx − σy) 2 + τ2 xy Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 23 / 30
- 31. Estado de Esfuerzos Planos Cı́rculo de Mohr Cı́rculo de Mohr Representación gráfica de las ecuaciones desarrolladas para σn y τnt. σn − 1 2 (σx + σy) = 1 2 (σx − σy) · cos(2θ) + τxy · sen(2θ) τnt = − 1 2 · (σx − σy) · sen(2θ) + τxy · cos(2θ) σn − 1 2 (σx + σy) 2 + τ2 nt = 1 2 (σx − σy) 2 + τ2 xy σprom = 1 2 (σx + σy) R = s 1 2 (σx − σy) 2 + τ2 xy Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 23 / 30
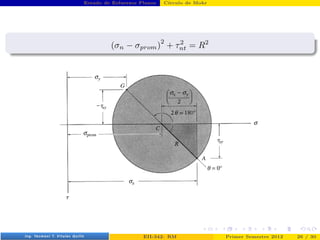
- 32. Estado de Esfuerzos Planos Cı́rculo de Mohr Cı́rculo de Mohr Representación gráfica de las ecuaciones desarrolladas para σn y τnt. σn − 1 2 (σx + σy) = 1 2 (σx − σy) · cos(2θ) + τxy · sen(2θ) τnt = − 1 2 · (σx − σy) · sen(2θ) + τxy · cos(2θ) σn − 1 2 (σx + σy) 2 + τ2 nt = 1 2 (σx − σy) 2 + τ2 xy σprom = 1 2 (σx + σy) R = s 1 2 (σx − σy) 2 + τ2 xy (σn − σprom) 2 + τ2 nt = R2 Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 23 / 30
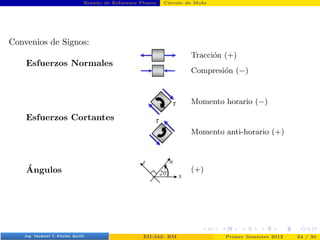
- 33. Estado de Esfuerzos Planos Cı́rculo de Mohr Convenios de Signos: Esfuerzos Normales Tracción (+) Compresión (−) Esfuerzos Cortantes Momento horario (−) Momento anti-horario (+) Ángulos (+) Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 24 / 30
- 34. Estado de Esfuerzos Planos Cı́rculo de Mohr (σn − σprom) 2 + τ2 nt = R2 Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 25 / 30
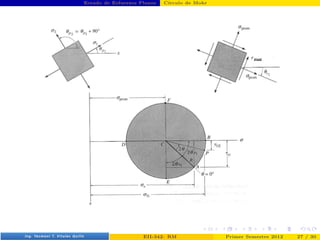
- 35. Estado de Esfuerzos Planos Cı́rculo de Mohr (σn − σprom) 2 + τ2 nt = R2 Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 26 / 30
- 36. Estado de Esfuerzos Planos Cı́rculo de Mohr Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 27 / 30
- 37. Estado de Esfuerzos Planos Problemas Problemas Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 28 / 30
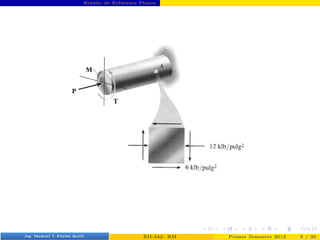
- 38. Estado de Esfuerzos Planos Problemas Problema 1 En el elemento diferencial mostrado en la figura, determinar los esfuerzo prin- cipales y máximo esfuerzo cortante con los planos sobre los que actúan Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 29 / 30
- 39. Estado de Esfuerzos Planos Problemas Problema 2 The state of stress at a point in a member is shown on the element. Determine the stress component acting on the inclined plan AB. Prof. Luis Pérez Pozo (PUCV) EII-342: RM Primer Semestre 2012 30 / 30