Metodos de analisis de estabilidad de taludes
- 1. METODOS DE ANALISIS DE ESTABILIDAD DE TALUDES En los métodos de análisis para estabilidad de taludes, en la practica la estabilidad se determina en términos de un factor de seguridad teniendo en cuenta todos los aspectos que afecten la estabilidad de un talud, como pueden ser los parámetros geomorfológicos, presencia de grietas de tensión, cargas dinámicas por sismos, la geometría del talud, propiedades de los suelos, flujo de agua, y todos los factores externos que puedan influir en el equilibrio de la estructura. No solo la determinación del factor de seguridad asegura el comportamiento del talud, pues no todos los factores se pueden matematizar en un modelo, pero da una idea del comportamiento basándose en superficies de falla, generalmente con figuras geométricas determinadas ya sean circulares planas, o semicirculares, ya que existen pocos modelos y aun presentan errores para superficies irregulares, pero aún falta investigación del tema, teniendo en cuenta que el suelo se comporta como material isotrópico. La falla en los taludes se pueden presentar en suelos en condiciones drenadas o no drenadas, dícese de no drenadas cuando la inestabilidad es causada por cambios de cargas, ya sea en la parte superior por aumento de cargas, o por remoción de materiales en la parte inferior del talud, en suelos de baja permeabilidad, donde el tiempo es insuficiente para drenar el agua durante el cambio de carga; usualmente los suelos tienen una alta permeabilidad, por lo que los análisis se realizan en condiciones drenadas. Los análisis en problemas de estabilidad se hacen suponiendo un sistema de esfuerzos efectivos o totales, debido a que la estabilidad del suelo esta regida por las presiones efectivas tanto en condición drenada como en no drenada, aunque en la realidad no se pueden determinar con exactitud los excesos en la presión de poros que se presentara por el cambio de carga (excavaciones, cambios del nivel del agua, colocación de rellenos, etc), pero igual los análisis se realizan con el sistema de esfuerzos totales o efectivos. Existen diferentes tipos de métodos de cálculo estabilidad de taludes, donde se clasifican en métodos numéricos y métodos de equilibrio limite. Los métodos de equilibrio limite plantean que las fuerzas actuantes y resistentes son iguales a lo largo de una superficie de falla, equivalentes a un factor de seguridad de 1.0, este análisis requiere información sobre la resistencia del suelo; el análisis se puede realizar estudiando la longitud total de la superficie de falla o dividiendo la masa de suelo en tajadas o dovelas, a partir del siglo XX se han desarrollado diversos métodos mejorando el sistema de dovelas y se manejan por iteraciones y cada uno tiene un grado de exactitud. Han existido diversos autores que han estudiado el tema y han hecho sus planteamientos acerca del análisis por equilibrio limite como lo han sido Fellenius (1.927), que plantea el método más común de dovelas, con superficies de fallas circulares y equilibrio de fuerzas, usado generalmente en taludes planos con alta presión de poros pues es muy impreciso, presenta bajos factores de seguridad aunque es muy usado por su simplicidad de hacerlo. También hay otros métodos como lo son el de Bishop (1.955) que plantea equilibrio de momentos en superficies circulares también, están en el Janbú (1.968), Spencer (1.967), Morgenstern & Price (1.965), que se explicaran adelante más detalladamente, que son aplicados a cualquier superficie de falla y plantea un equilibrio de momentos y fuerzas; existen otros métodos como lo son el de Sarma (1.973) donde desarrolla una relación entre el coeficiente sísmico para producir la falla, obtenido por el método de las dovelas y el factor de seguridad, donde el factor de seguridad estático corresponde al caso cero de coeficiente sísmico; están el de Lowe & Karafiath (1.960), por elementos finitos y por espiral logarítmica, esta ultima solo aplica a superficies de falla de forma espiral logarítmica. El factor de seguridad es usado para saber cuál es el factor de amenaza de falla del talud en el peor de los comportamientos de este; Fellenius (1.927) presento el factor de seguridad como “la
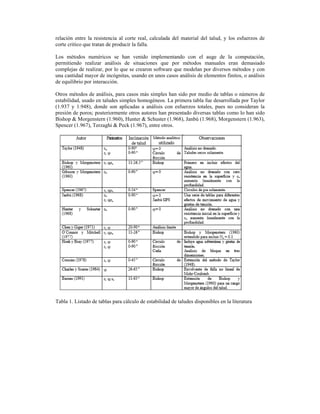
- 2. relación entre la resistencia al corte real, calculada del material del talud, y los esfuerzos de corte critico que tratan de producir la falla. Los métodos numéricos se han venido implementando con el auge de la computación, permitiendo realizar análisis de situaciones que por métodos manuales eran demasiado complejas de realizar, por lo que se crearon software que modelan por diversos métodos y con una cantidad mayor de incógnitas, usando en unos casos análisis de elementos finitos, o análisis de equilibrio por interacción. Otros métodos de análisis, para casos más simples han sido por medio de tablas o números de estabilidad, usado en taludes simples homogéneos. La primera tabla fue desarrollada por Taylor (1.937 y 1.948), donde son aplicadas a análisis con esfuerzos totales, pues no consideran la presión de poros; posteriormente otros autores han presentado diversas tablas como lo han sido Bishop & Morgenstern (1.960), Hunter & Schuster (1.968), Janbú (1.968), Morgenstern (1.963), Spencer (1.967), Terzaghi & Peck (1.967), entre otros. Tabla 1. Listado de tablas para cálculo de estabilidad de taludes disponibles en la literatura
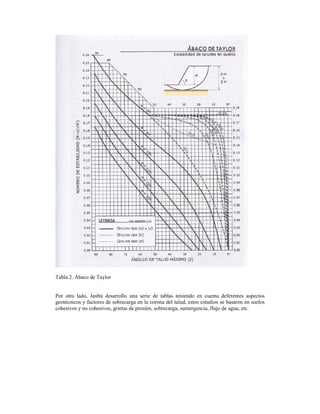
- 3. Los métodos se pueden clasificar de la siguiente manera: Grafica 1. Clasificación de métodos de cálculo de estabilidad de taludes MÉTODOS DE ANÁLISIS DE EQUILIBRIO LÍMITE Tablas de diseño de Taylor (1.937-1.948) y Janbú (1.968) Las tablas de diseño de Taylor de basan en un análisis del talud que permite encontrar la máxima inclinación (α) posible del talud en función de la altura (H), ángulo de fricción (φ), peso específico (γ), cohesión (c) y factor de seguridad (F.S). Se realiza en condiciones no drenadas, y para un mayor uso de la gráfica dada por Taylor determino una ecuación del número de estabilidad (N), definido por: . . . Usualmente se tienen los valores de la cohesión, el peso específico, el N se obtiene de la gráfica, el factor de seguridad con lo que obtenemos la altura critica del talud, esta está relacionada con la carga vertical, formadas por sobrecargas muertas y vivas según el uso del talud.
- 4. Tabla 2. Ábaco de Taylor Por otro lado, Janbú desarrollo una serie de tablas teniendo en cuenta deferentes aspectos geotécnicos y factores de sobrecarga en la corona del talud, estos estudios se basaron en suelos cohesivos y no cohesivos, grietas de presión, sobrecarga, sumergencia, flujo de agua, etc.
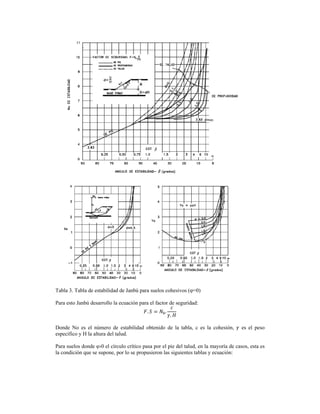
- 5. Tabla 3. Tabla de estabilidad de Janbú para suelos cohesivos (φ=0) Para esto Janbú desarrollo la ecuación para el factor de seguridad: . . . Donde No es el número de estabilidad obtenido de la tabla, c es la cohesión, es el peso específico y H la altura del talud. Para suelos donde φ›0 el círculo crítico pasa por el pie del talud, en la mayoría de casos, esta es la condición que se supone, por lo se propusieron las siguientes tablas y ecuación:
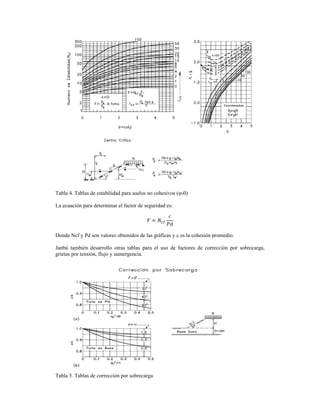
- 6. Tabla 4. Tablas de estabilidad para suelos no cohesivos (φ›0) La ecuación para determinar el factor de seguridad es: Donde Ncf y Pd son valores obtenidos de las gráficas y c es la cohesión promedio. Janbú también desarrollo otras tablas para el uso de factores de corrección por sobrecarga, grietas por tensión, flujo y sumergencia. Tabla 5. Tablas de corrección por sobrecarga
- 7. Tabla 6. Tablas de corrección por sumergencia y flujo Tabla 7. Tablas de factores de corrección por grietas de tensión
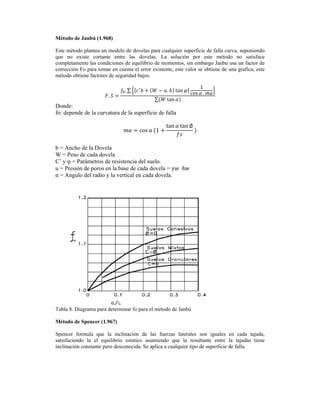
- 8. Método de Janbú (1.968) Este método plantea un modelo de dovelas para cualquier superficie de falla curva, suponiendo que no existe cortante entre las dovelas. La solución por este método no satisface completamente las condiciones de equilibrio de momentos, sin embargo Janbu usa un factor de corrección Fo para tomar en cuenta el error existente, este valor se obtiene de una grafica; este método obtiene factores de seguridad bajos. . . ∑ . tan 1 cos . ∑ tan Donde: fo: depende de la curvatura de la superficie de falla cos ⍺ 1 tan tan ∅ b = Ancho de la Dovela W = Peso de cada dovela C’ y φ = Parámetros de resistencia del suelo. u = Presión de poros en la base de cada dovela = α = Angulo del radio y la vertical en cada dovela. Tabla 8. Diagrama para determinar fo para el método de Janbú Método de Spencer (1.967) Spencer formula que la inclinación de las fuerzas laterales son iguales en cada tajada, satisfaciendo la el equilibrio estatico asumiendo que la resultante entre la tajadas tiene inclinación constante pero desconocida. Se aplica a cualquier tipo de superficie de falla.
- 9. Método de Morgenstern & Price En este método se plantea que las fuerzas laterales siguen un sistema predeterminado, donde la inclinación de la resultante de las fuerzas varía en función de: Este método satisface las ecuaciones de equilibrio. MÉTODOS NUMÉRICOS DE ANÁLISIS Análisis por elementos finitos El método de elementos finitos fue introducido por Clough & Woodward (1.967), que resuelve los problemas de los análisis de equilibrio limite, dividiendo la masa de suelo en elementos discretos denominados finitos, interconectados por nodos y bordes definidos. Se basa en la formulación de desplazamientos que nos da como resultados esfuerzos y desplazamientos de los puntos de los nodos. La falla se presenta de manera progresiva, es decir, que no falla simultáneamente en todos los puntos de la estructura. Para realizarse un análisis por elementos finitos deben cumplirse que el equilibrio se mantenga en cada punto, por medio de un análisis con la teoría elástica que describe las relaciones esfuerzo-deformación, además de que las condiciones de esfuerzos de frontera deben satisfacerse. Existen diversos métodos numéricos usados, pero unos de los más comunes son FLAC y UDEC. El FLAC divide la masa en una malla de acuerdo a su geometría, donde se pueden seleccionar varias relaciones de esfuerzo-deformación; y en el UDEC el talud se divide en bloques de acuerda a un sistema de grietas, las cuales pueden ser rígidas o deformables. Grafica 2. Malla típica para método de análisis por elementos finitos
- 10. Métodos numéricos análisis a elementos finitos 3D En los métodos de análisis en tres dimensiones varios autores han trabajado al respecto pero el más común y nombrado es el método implantado por Yamagami & Jiang (1.996), donde usa las ecuaciones del factor de seguridad de Janbú, con un esquema de minimización programado, por el que se obtiene la superficie critica de falla en 3D, con su respectiva dirección de movimiento y factor de seguridad. Grafica 3. Análisis de falla Yamagami & Jiang (1.996)
- 11. BIBLIOGRAFÍA Manual de Taludes. Instituto Geológico y Minero de España (IGME). 1.986. Deslizamientos y Estabilidad de Taludes en zonas tropicales. Jaime Suarez Diaz. Universidad Industrial de Santander. 1.998. Notas sobre análisis de estabilidad de Taludes. Jorge E. Alva Hurtado. Universidad Nacional de Colombia. 1.994 Manual de Carreteras. Luis Bañon Blazques. 2.000 Notas de clase, estabilidad de taludes. Diego Olaya. UGC. 2.015 Tablas Tabla 1. Tomada de Deslizamientos y Estabilidad de Taludes en zonas tropicales, Jaime Suarez Díaz. UIS. Tabla 2. Ábaco de Taylor. Tomada de Manual de Carreteras, Luis Bañon Blazques Tabla 3. Tabla de estabilidad de Janbú para suelos cohesivos (φ=0). Tomada de Deslizamientos y Estabilidad de Taludes en zonas tropicales, Jaime Suarez Díaz. UIS. Tabla 4. Tablas de estabilidad para suelos no cohesivos (φ›0). Tomada de Deslizamientos y Estabilidad de Taludes en zonas tropicales, Jaime Suarez Díaz. UIS. Tabla 5. Tablas de corrección por sobrecarga. Tomada de Deslizamientos y Estabilidad de Taludes en zonas tropicales, Jaime Suarez Díaz. UIS. Tabla 6. Tablas de corrección por sumergencia y flujo. Tomada de Deslizamientos y Estabilidad de Taludes en zonas tropicales, Jaime Suarez Díaz. UIS. Tabla 7. Tablas de factores de corrección por grietas de tensión. Tomada de Deslizamientos y Estabilidad de Taludes en zonas tropicales, Jaime Suarez Díaz. UIS. Tabla 8. Diagrama para determinar fo para el método de Janbú. Tomada de Manual de Taludes, IGME. Gráficos Grafica 1. Tomada de notas de clase de estabilidad de taludes. Diego Olaya. Grafica 2. Malla típica para método de análisis por elementos finitos. Tomada de Deslizamientos y Estabilidad de Taludes en zonas tropicales, Jaime Suarez Díaz. UIS. Grafica 3. Análisis de falla Yamagami & Jiang (1.996). Tomada de Deslizamientos y Estabilidad de Taludes en zonas tropicales, Jaime Suarez Díaz. UIS.