circulo de morh, mecanica de materiales.
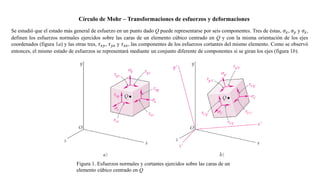
- 1. Círculo de Mohr – Transformaciones de esfuerzos y deformaciones Se estudió que el estado más general de esfuerzo en un punto dado Q puede representarse por seis componentes. Tres de éstas, 𝜎𝑥, 𝜎𝑦 y 𝜎𝑧, definen los esfuerzos normales ejercidos sobre las caras de un elemento cúbico centrado en Q y con la misma orientación de los ejes coordenados (figura 1a) y las otras tres, 𝜏𝑥𝑦, 𝜏𝑦𝑧 y 𝜏𝑧𝑥, las componentes de los esfuerzos cortantes del mismo elemento. Como se observó entonces, el mismo estado de esfuerzos se representará mediante un conjunto diferente de componentes si se giran los ejes (figura 1b). Figura 1. Esfuerzos normales y cortantes ejercidos sobre las caras de un elemento cúbico centrado en Q
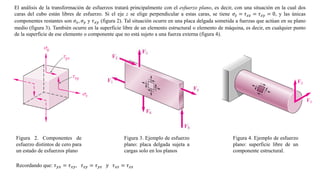
- 2. El análisis de la transformación de esfuerzos tratará principalmente con el esfuerzo plano, es decir, con una situación en la cual dos caras del cubo están libres de esfuerzo. Si el eje z se elige perpendicular a estas caras, se tiene 𝜎𝑧 = 𝜏𝑧𝑥 = 𝜏𝑧𝑦 = 0, y las únicas componentes restantes son 𝜎𝑥, 𝜎𝑦 y 𝜏𝑥𝑦 (figura 2). Tal situación ocurre en una placa delgada sometida a fuerzas que actúan en su plano medio (figura 3). También ocurre en la superficie libre de un elemento estructural o elemento de máquina, es decir, en cualquier punto de la superficie de ese elemento o componente que no está sujeto a una fuerza externa (figura 4). Figura 2. Componentes de esfuerzo distintos de cero para un estado de esfuerzos plano Figura 3. Ejemplo de esfuerzo plano: placa delgada sujeta a cargas solo en los planos Figura 4. Ejemplo de esfuerzo plano: superficie libre de un componente estructural. Recordando que: 𝜏𝑦𝑥 = 𝜏𝑥𝑦, 𝜏𝑧𝑦 = 𝜏𝑦𝑧 𝑦 𝜏𝑥𝑧 = 𝜏𝑧𝑥
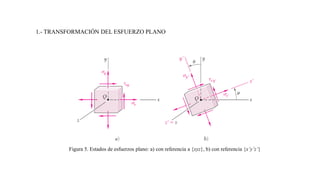
- 3. Figura 5. Estados de esfuerzos plano: a) con referencia a {xyz}, b) con referencia {x’y’z’} 1.- TRANSFORMACIÓN DEL ESFUERZO PLANO
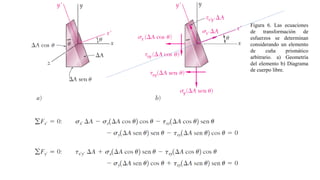
- 4. Figura 6. Las ecuaciones de transformación de esfuerzos se determinan considerando un elemento de cuña prismático arbitrario. a) Geometría del elemento b) Diagrama de cuerpo libre.
- 5. (1) (2) (3) (4) la ecuación (1) se escribe como sigue:
- 6. Usando las relaciones (3) se tiene la ecuación (2) como (5) (6) La expresión para el esfuerzo normal 𝜎𝑦′ se obtiene remplazando 𝜃 en la ecuación (5) por el ángulo 𝜃 + 90° que el eje 𝑦′ forma con el eje x. Como cos 2θ + 180° = −cos 2θ y sen 2θ + 180° = −sen 2θ, se tiene (7) Sumando miembro a miembro las ecuaciones (5) y (7) (8) Nota: Como 𝜎𝑧 = 𝜎𝑧′ = 0, se verifica que la suma de los esfuerzos normales ejercidos sobre un elemento cúbico de material es independiente de la orientación del elemento.
- 7. ESFUERZOS PRINCIPALES. ESFUERZO CORTANTE MÁXIMO (9) (10) se escribe la identidad (9) en la forma Figura 7. Relación circular de esfuerzos transformados Figura 8. Formación equivalente del círculo de transformación del esfuerzo. Nota: Puede observarse que, debido a la simetría del círculo con respecto al eje horizontal, se habría obtenido el mismo resultado si, en lugar de graficar M, se hubiera graficado un punto N de abscisa 𝜎𝑥′ y ordenada 𝜏𝑥′𝑦′(figura 8).