Esfuerzos 2D
7 recomendaciones•3,325 vistas
El documento presenta los fundamentos de la geomecánica bidimensional. Explica conceptos como esfuerzos normales, cortantes y principales, así como las convenciones y metodologías para su determinación, incluyendo el análisis analítico, matricial y gráfico usando el círculo de Mohr. Finalmente, propone ejercicios prácticos para aplicar los conocimientos.
![Referencias
• Fritzler, I. (2016): Ayudantía 0: Círculo de Mohr. Mecánica de Rocas I. Universidad de
Santiago de Chile, Santiago, Chile.
• Jarufe, J. (2016): Unidad II: Esfuerzos [Material de Clase]. Fundamentos de Geomecánica.
Universidad de Santiago de Chile, Santiago, Chile.
• Yelicich, V. (2016): Ayudantía: Círculo de Mohr. Mecánica de Rocas I. Universidad de
Santiago de Chile, Región Metropolitana, Santiago.](https://image.slidesharecdn.com/ayudanta0-esfuerzos2d-171214025239/85/Esfuerzos-2D-26-320.jpg)
Esfuerzos 2D
- 1. Mecánica de Rocas I Fundamentos de Geomecánica Ayudantía: “Esfuerzos 2D” Profesor: Juan Jarufe Preparado por: Ivo Fritzler 1° Semestre 2018
- 2. Contenido • Idea General • Teoría • Esfuerzos • Convención de esfuerzos • Convención angular • Metodologías • Analítico • Matricial • Tensor Bidimensional • Gráfico • Círculo de Mohr • Ejercicios • Referencias
- 3. Idea General - Primer acercamiento al concepto de esfuerzo. - Representar el estado tensional de manera bidimensional para caracterizar ensayos de roca, algún sector de un macizo rocoso o una estructura mayor (falla). - Conocer las metodologías existentes para la determinación de estos (Analítica, Gráfica y Matricial) - Comprender las convenciones propuestas por las tres metodologías, para evitar confusiones en el trayecto del curso. 𝝈 𝑵 𝝉 𝑷 𝑸 Estado tensional en probeta de roca Estado tensional en estructura mayor (falla) Estado tensional in situ en macizo rocoso
- 4. Teoría • Esfuerzos “Carga distribuida en unidad de área” • Esfuerzo Normal • Esfuerzo Cortante • Esfuerzos Principales 𝜎 𝑁 = 𝑃 𝐴 𝜏 = 𝑉 2𝐴 P corresponde a una carga perpendicular a un área A. V corresponde a una carga paralela a una sección transversal A en la cual genera corte 𝜎1, 𝜎2, 𝜎3, 𝑃, 𝑄 𝜎1,2,3: Esfuerzos Principales considerando sistema 3D P, Q: Esfuerzos Principales Secundarios considerando sistema 2D
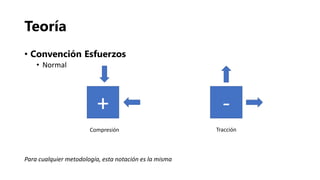
- 5. Teoría • Convención Esfuerzos • Normal + - Compresión Tracción Para cualquier metodología, esta notación es la misma
- 6. Teoría • Convención Esfuerzos • Cortante + - - + Cortante anti horario positiva Cortante horario negativa Aplica para: • Metodología Gráfica • Círculo de Mohr Cortante anti horario negativa Cortante horario positiva Aplica para: • Metodología Analítica • Metodología Matricial • Tensor 2D
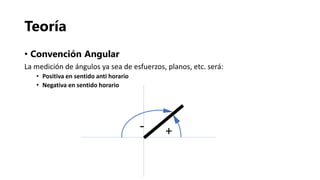
- 7. Teoría • Convención Angular La medición de ángulos ya sea de esfuerzos, planos, etc. será: • Positiva en sentido anti horario • Negativa en sentido horario +-
- 8. Teoría • Metodologías • Analítico Si deseo rotar esfuerzos a un plano particular o obtener esfuerzos cartesianos a partir de esfuerzos distintos de x,y,z. Si deseo obtener la magnitud de esfuerzos principales secundarios (P,Q) y la orientación de estos en el plano 2D correspondiente
- 9. Teoría • Metodologías • Matricial 𝜎𝑥𝑦 = 𝜎𝑥 𝜏 𝑥𝑦 𝜏 𝑦𝑥 𝜎 𝑦 𝐿 = cos 𝜃 − sin 𝜃 sin 𝜃 cos 𝜃 𝜎𝑥´𝑦´ = 𝐿 𝑇 ∙ 𝜎𝑥𝑦 ∙ 𝐿 Donde: 𝜎 𝑥𝑦: Tensor inicial 𝐿, 𝐿 𝑇: Matrices de cosenos directores sin trasponer y traspuesta respectivamente 𝜃: Ángulo de inclinación o beta del azimut, dependerá de la dimensión 2D analizada 𝜎 𝑥´𝑦´: Tensor resultante de la nueva orientación evaluada
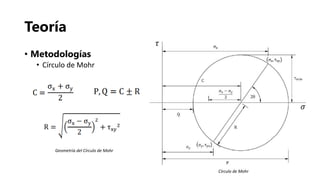
- 10. Teoría • Metodologías • Círculo de Mohr Geometría del Círculo de Mohr Círculo de Mohr
- 11. Teoría • Metodologías • Círculo de Mohr • Teoría del Polo Permite evaluar algún plano desconocido de un elemento, a partir de la intersección entre dos planos conocidos del mismo elemento, esta intersección se denomina Polo. Por evaluar entiéndase como determinar el estado tensional y orientaciones de esfuerzos que lo componen.
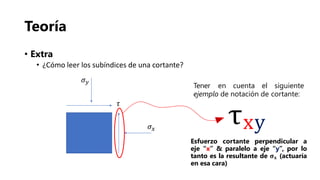
- 12. Teoría • Extra • ¿Cómo leer los subíndices de una cortante? Tener en cuenta el siguiente ejemplo de notación de cortante: τxy Esfuerzo cortante perpendicular a eje “x” & paralelo a eje “y”, por lo tanto es la resultante de 𝛔 𝐱 (actuaría en esa cara) 𝜎 𝑦 𝜎𝑥 𝜏
- 13. Ejercicio En un sector, se ha realizado un análisis del estado tensional presente, mediante celdas triaxiales, obteniendo la siguiente información: Además, se detectó una falla en el sector con orientación NS/50E. Se solicita: Determinar estado tensional en falla y esfuerzos principales secundarios (magnitud y orientación) para ese plano, mediante las siguientes metodologías: ✓ Analítico ✓ Matricial ✓ Gráfico 𝜎 𝑥 𝜏 𝑥𝑦 𝜏 𝑥𝑧 𝜏 𝑦𝑧 𝜎 𝑦 𝜏 𝑦𝑧 𝜏 𝑧𝑥 𝜏 𝑧𝑦 𝜎𝑧 = 26 3 −5 3 13 −4 −5 −4 6
- 14. W E Solución • Desglosando información que necesitamos para una falla NS/50E • Obtención de estado tensional • Método analítico 𝜎𝑥𝑧 = 26 −5 −5 6 50° 𝝈 𝑵 = 𝟏𝟒. 𝟑𝟑 𝑴𝑷𝒂 𝝉 = −𝟏𝟏. 𝟎𝟓 𝑴𝑷𝒂 𝜽 = 𝟒𝟎° 𝑷 = 𝟐𝟕. 𝟏𝟖 𝑴𝑷𝒂, 𝜽 𝑷 = −𝟏𝟐. 𝟔𝟒 ° 𝑸 = 𝟒. 𝟖𝟐 𝑴𝑷𝒂, 𝜽 𝑸 = 𝟕𝟕. 𝟑𝟔°
- 15. Solución • Método Matricial 𝐿 = 0.8090 −0.5877 0.5877 0.8090 𝜎𝑥´𝑦´ = 0.8090 0.5877 −0.5877 0.8090 ∙ 26 −5 −5 6 ∙ 0.8090 −0.5877 0.5877 0.8090 𝜎 𝑥𝑧 = 26 −5 −5 6 𝜽 = 𝟒𝟎° 𝐿 𝑇 = 0.8090 0.5877 −0.5877 0.8090 𝜎𝑥´𝑦´ = 14.33 −11.05 −11.05 17.66 𝝈 𝑵 = 𝟏𝟒. 𝟑𝟑 𝑴𝑷𝒂 𝝉 = −𝟏𝟏. 𝟎𝟓 𝑴𝑷𝒂 𝜎𝑥´𝑦´ = 14.33 − λ −11.05 −11.05 17.66 − λ λ1 = 27.17, λ2 = 4.82 𝑷 = 𝟐𝟕. 𝟏𝟕 𝑴𝑷𝒂 𝑸 = 𝟒. 𝟖𝟐 𝑴𝑷𝒂 𝜽 𝑷 = −𝟏𝟐. 𝟔𝟒 ° 𝜽 𝒒 = 𝟕𝟕. 𝟑𝟔°
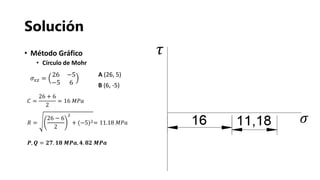
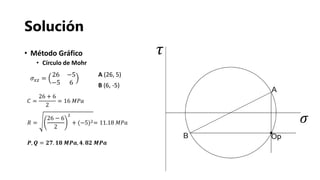
- 16. Solución • Método Gráfico • Círculo de Mohr 𝐶 = 26 + 6 2 = 16 𝑀𝑃𝑎 𝑅 = 26 − 6 2 2 + (−5)2= 11.18 𝑀𝑃𝑎 𝑷, 𝑸 = 𝟐𝟕. 𝟏𝟖 𝑴𝑷𝒂, 𝟒. 𝟖𝟐 𝑴𝑷𝒂 𝜎 𝑥𝑧 = 26 −5 −5 6 𝜏 𝜎 A (26, 5) B (6, -5)
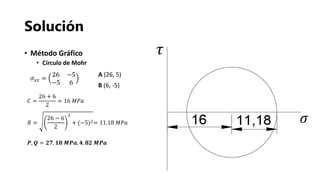
- 17. Solución • Método Gráfico • Círculo de Mohr 𝐶 = 26 + 6 2 = 16 𝑀𝑃𝑎 𝑅 = 26 − 6 2 2 + (−5)2= 11.18 𝑀𝑃𝑎 𝑷, 𝑸 = 𝟐𝟕. 𝟏𝟖 𝑴𝑷𝒂, 𝟒. 𝟖𝟐 𝑴𝑷𝒂 𝜎 𝑥𝑧 = 26 −5 −5 6 𝜏 𝜎 A (26, 5) B (6, -5)
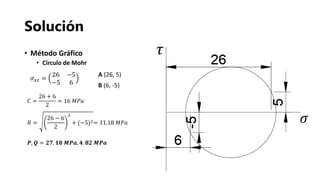
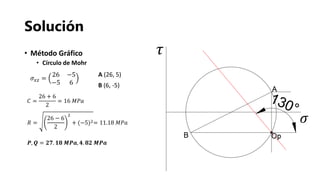
- 18. Solución • Método Gráfico • Círculo de Mohr 𝐶 = 26 + 6 2 = 16 𝑀𝑃𝑎 𝑅 = 26 − 6 2 2 + (−5)2= 11.18 𝑀𝑃𝑎 𝑷, 𝑸 = 𝟐𝟕. 𝟏𝟖 𝑴𝑷𝒂, 𝟒. 𝟖𝟐 𝑴𝑷𝒂 𝜎 𝑥𝑧 = 26 −5 −5 6 𝜏 𝜎 A (26, 5) B (6, -5)
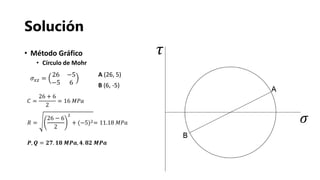
- 19. Solución • Método Gráfico • Círculo de Mohr 𝐶 = 26 + 6 2 = 16 𝑀𝑃𝑎 𝑅 = 26 − 6 2 2 + (−5)2= 11.18 𝑀𝑃𝑎 𝑷, 𝑸 = 𝟐𝟕. 𝟏𝟖 𝑴𝑷𝒂, 𝟒. 𝟖𝟐 𝑴𝑷𝒂 𝜎 𝑥𝑧 = 26 −5 −5 6 𝜏 𝜎 A (26, 5) B (6, -5)
- 20. Solución • Método Gráfico • Círculo de Mohr 𝐶 = 26 + 6 2 = 16 𝑀𝑃𝑎 𝑅 = 26 − 6 2 2 + (−5)2= 11.18 𝑀𝑃𝑎 𝑷, 𝑸 = 𝟐𝟕. 𝟏𝟖 𝑴𝑷𝒂, 𝟒. 𝟖𝟐 𝑴𝑷𝒂 𝜎 𝑥𝑧 = 26 −5 −5 6 𝜏 𝜎 A (26, 5) B (6, -5)
- 21. Solución • Método Gráfico • Círculo de Mohr 𝐶 = 26 + 6 2 = 16 𝑀𝑃𝑎 𝑅 = 26 − 6 2 2 + (−5)2= 11.18 𝑀𝑃𝑎 𝑷, 𝑸 = 𝟐𝟕. 𝟏𝟖 𝑴𝑷𝒂, 𝟒. 𝟖𝟐 𝑴𝑷𝒂 𝜎 𝑥𝑧 = 26 −5 −5 6 𝜏 𝜎 A (26, 5) B (6, -5)
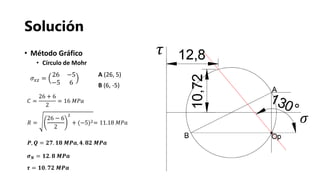
- 22. Solución • Método Gráfico • Círculo de Mohr 𝐶 = 26 + 6 2 = 16 𝑀𝑃𝑎 𝑅 = 26 − 6 2 2 + (−5)2= 11.18 𝑀𝑃𝑎 𝑷, 𝑸 = 𝟐𝟕. 𝟏𝟖 𝑴𝑷𝒂, 𝟒. 𝟖𝟐 𝑴𝑷𝒂 𝜎 𝑥𝑧 = 26 −5 −5 6 𝝈 𝑵 = 𝟏𝟐. 𝟖 𝑴𝑷𝒂 𝝉 = 𝟏𝟎. 𝟕𝟐 𝑴𝑷𝒂 𝜏 𝜎 A (26, 5) B (6, -5)
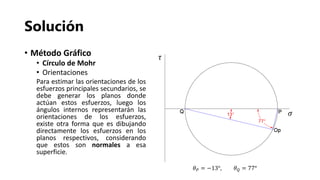
- 23. Solución • Método Gráfico • Círculo de Mohr • Orientaciones Para estimar las orientaciones de los esfuerzos principales secundarios, se debe generar los planos donde actúan estos esfuerzos, luego los ángulos internos representarán las orientaciones de los esfuerzos, existe otra forma que es dibujando directamente los esfuerzos en los planos respectivos, considerando que estos son normales a esa superficie. 𝜃 𝑃 = −13°, 𝜃 𝑄 = 77° 𝜏 𝜎
- 24. Ejercicio Propuesto La figura que se presenta a continuación, corresponde a la representación de un pozo de agua vertical, afectado por esfuerzos combinados en sus contornos. Se tiene la siguiente información del estado tensional Se solicita determinar por la metodología que usted estime conveniente. a. Esfuerzos principales y orientación b. Esfuerzos combinados (normal y cortante) NS y EW con orientación de esfuerzos normales c. Suponga una falla N35W presente en la excavación propuesta, determine su estado tensional con orientación de la normal y cortante 𝜎 𝑥´ (MPa) 𝜎 𝑦´ (MPa) 𝜏 𝑦´𝑥´ (MPa) 13 21 4
- 25. Solución a.Q=11.35 MPa, orientación 143°, P=22.65 MPa, orientación 53° b. NS 18.48 MPa, 5.45 MPa, orientación 90°, EW 15.53 MPa, -5.45 MPa, orientación 0° c. Magnitud normal: 21.62 MPa, cortante: 3.25 MPa, Orientación normal 125°, cortante 35° * El ángulo de orientación de los esfuerzos propuestos en las respuestas puede tener otro valor (el suplemento de los ángulos propuestos) con otro sentido (medición horaria - negativo) *
- 26. Referencias • Fritzler, I. (2016): Ayudantía 0: Círculo de Mohr. Mecánica de Rocas I. Universidad de Santiago de Chile, Santiago, Chile. • Jarufe, J. (2016): Unidad II: Esfuerzos [Material de Clase]. Fundamentos de Geomecánica. Universidad de Santiago de Chile, Santiago, Chile. • Yelicich, V. (2016): Ayudantía: Círculo de Mohr. Mecánica de Rocas I. Universidad de Santiago de Chile, Región Metropolitana, Santiago.