Tema 7. diedrico directo fundamentos
- 1. DIBUJO TÉCNICO 2º BACHILLERATOTEMA 7. DIÉDRICO DIRECTOFundamentosRecta y planoInterseccionesParalelismoPerpendicularidad
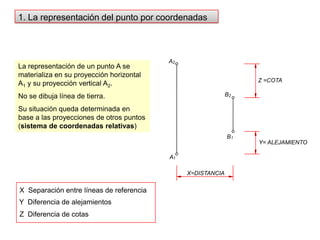
- 2. A2Z =COTAB2B1Y= ALEJAMIENTOA1X=DISTANCIA1. La representación del punto por coordenadasLa representación de un punto A se materializa en su proyección horizontal A1 y su proyección vertical A2.No se dibuja línea de tierra.Su situación queda determinada en base a las proyecciones de otros puntos (sistema de coordenadas relativas)X Separación entre líneas de referenciaY Diferencia de alejamientosZ Diferencia de cotas
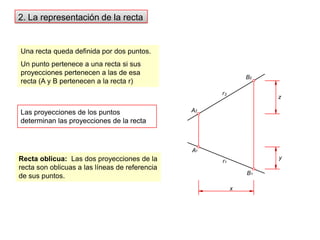
- 3. B2r2zA2A1yr1B1x2. La representación de la rectaUna recta queda definida por dos puntos. Un punto pertenece a una recta si sus proyecciones pertenecen a las de esa recta (A y B pertenecen a la recta r)Las proyecciones de los puntos determinan las proyecciones de la rectaRecta oblicua: Las dos proyecciones de la recta son oblicuas a las líneas de referencia de sus puntos.
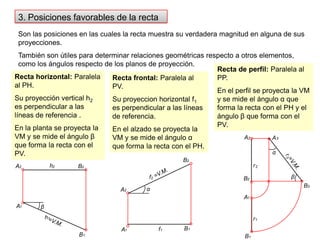
- 4. A2BBB222fr22h2AA22A1B1BB11AAfr1111h13. Posiciones favorables de la rectaSon las posiciones en las cuales la recta muestra su verdadera magnitud en alguna de sus proyecciones.También son útiles para determinar relaciones geométricas respecto a otros elementos, como los ángulos respecto de los planos de proyección. Recta de perfil: Paralela al PP. En el perfil se proyecta la VM y se mide el ángulo α que forma la recta con el PH y el ánguloβ que forma con el PV.Recta horizontal: Paralela al PH. Su proyección vertical h2 es perpendicular a las líneas de referencia .En la planta se proyecta la VM y se mide el ángulo β que forma la recta con el PV.Recta frontal: Paralela al PV. Su proyeccion horizontal f1 es perpendicular a las líneas de referencia.En el alzado se proyecta la VM y se mide el ángulo α que forma la recta con el PH.A3ααβr3=V.M.β=V.M.B3=V.M.
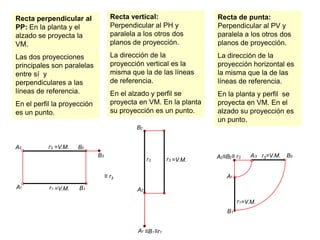
- 5. ≡B2≡ r2rr32A2BB22A1B1r2AA22B1r1ArA1≡r111≡B1Recta vertical: Perpendicular al PH y paralela a los otros dos planos de proyección. La dirección de la proyección vertical es la misma que la de las líneas de referencia.En el alzado y perfil se proyecta en VM. En la planta su proyección es un punto.Recta de punta: Perpendicular al PV y paralela a los otros dos planos de proyección. La dirección de la proyección horizontal es la misma que la de las líneas de referencia.En la planta y perfil se proyecta en VM. En el alzado su proyección es un punto.Recta perpendicular al PP: En la planta y el alzado se proyecta la VM. Las dos proyecciones principales son paralelas entre sí y perpendiculares a las líneas de referencia.En el perfil la proyección es un punto.Br3=V.M.A33=V.M.=V.M.B3≡ r3=V.M.=V.M.
- 6. A2B2r2r2N2MA21B1r1M1r1N14. Pertenencia de punto a rectaDada una recta r y el punto M, para que el punto pertenezca a la recta es necesario que las proyecciones del punto se encuentren sobre las proyecciones del mismo nombre en la rectaCCC213A3αEn el caso de la recta de perfil no es suficiente con comprobar las proyecciones horizontal y vertical y en el caso del punto C nos hemos de auxiliar de la proyección de perfil para comprobar que no pertenece a la recta. r3=V.M.βB3
- 7. rr22ss22PP22PP11rr11s1s15. Condición de corte de dos rectasLa condición para que dos rectas se corten es que tengan un punto en común.Cuando no se da esta circunstancia las dos rectas se cruzan en el espacio.
- 8. 6. Proyecciones auxiliares de una recta (por cambio de plano)Además de la proyección de perfil de una recta, a veces es conveniente disponer de otras proyecciones auxiliares para lo que necesitaremos cambiar la posición de uno de los dos planos de proyección principales.B2B2Conversión de una recta oblicua en frontal:Conversión de una recta oblicua en horizontal: A2A2A1A1B1’A2’B1B1A1’yyzzVMVMB2’
- 9. B2r2N2CP22M2A2A1M1r1PC1N11B17. Representación del planoLa mejor manera de representar un plano es por medio del polígono más simple (triángulo) perteneciente a dicho plano8. Pertenencia recta y punto a un planoDado un polígono ABC que define un plano y el punto PSe traza una de las proyecciones de una recta auxiliar R que pase por PSe localizan las proyecciones de la intersección de R con dos rectas del plano para que R esté contenida en dicho plano (M y N)Trazar la otra proyección de RSe comprueba que el punto P esté contenido en R
- 10. 9. Rectas notables del planoRecta horizontal del plano: Paralela al PH de referencia.Recta frontal del plano: Paralela al PV de referenciah2f2h1f1Recta de máxima pendiente: Perpendicular a una horizontal del planoRecta de máxima inclinación: Perpendicular a una frontal del planom2n2m1n1
- 11. B2r2s2A22P2C2C11A1P1r1sB11r2P2r1P110. Formas de determinar un planoLa forma más habitual de representar un plano en diédrico directo es mediante una forma poligonal cerrada, pero desde el punto de vista conceptual el plano puede venir determinado por:Dos rectas que se cortanDos rectas paralelasr2s2A2C2r1s1B2D2A1C1D1B1Tres puntos no alineadosUna recta y un punto exterior
- 12. n2mf22PhP222n1fP11P1m1h1Los dos siguientes son casos particulares de dos rectas que se cortan:Con una recta de máxima pendienteCon una recta de máxima inclinación
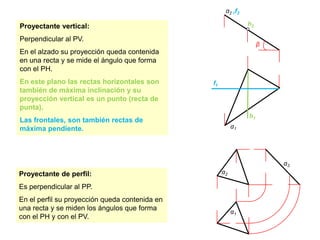
- 13. 11. Posiciones del plano favorablesLas posiciones que un plano puede ocupar en relación con los planos de proyección son: oblicuo, perpendicular y paralelo. Las posiciones favorables del plano son aquellas en las que el plano muestra su verdadera magnitud o aquellas que son útiles para resolver relaciones geométricas, como ángulos o intersecciones.Plano perpendicular a los de proyección o planos proyectantesf2Proyectante horizontal: Perpendicular al PH. En la planta su proyección queda contenida en una recta y se mide el ángulo β de este plano con el PV.En este plano las rectas horizontales son también de máxima inclinación.Las frontales, cuya proyección horizontal es un punto (recta vertical) son también rectas de máxima pendiente.α2h2βf1α1≡h1
- 14. Proyectante vertical: Perpendicular al PV. En el alzado su proyección queda contenida en una recta y se mide el ángulo que forma con el PH.En este plano las rectas horizontales son también de máxima inclinación y su proyección vertical es un punto (recta de punta).Las frontales, son también rectas de máxima pendiente.h2≡f2h1α2f1α3Proyectante de perfil: Es perpendicular al PP. En el perfil su proyección queda contenida en una recta y se miden los ángulos que forma con el PH y con el PV.α2βα1α1
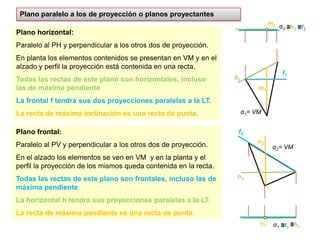
- 15. n2m2Plano paralelo a los de proyección o planos proyectantesPlano horizontal: Paralelo al PH y perpendicular a los otros dos de proyección. En planta los elementos contenidos se presentan en VM y en el alzado y perfil la proyección está contenida en una recta.Todas las rectas de este plano son horizontales, incluso las de máxima pendiente.La frontal f tendrá sus dos proyecciones paralelas a la LT. La recta de máxima inclinación es una recta de punta.α2≡h2m1n1≡f2h1Plano frontal: Paralelo al PV y perpendicular a los otros dos de proyección. En el alzado los elementos se ven en VM y en la planta y el perfil la proyección de los mismos queda contenida en la recta.Todas las rectas de este plano son frontales, incluso las de máxima pendiente.La horizontal h tendrá sus proyecciones paralelas a la LT. La recta de máxima pendiente es una recta de punta.f2α1= VMf1α2= VMh2≡h1≡f1α1
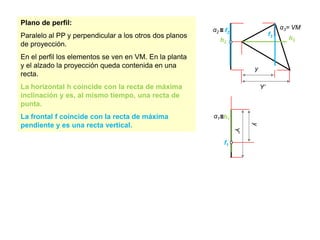
- 16. Plano de perfil:Paralelo al PP y perpendicular a los otros dos planos de proyección. En el perfil los elementos se ven en VM. En la planta y el alzado la proyección queda contenida en una recta.La horizontal h coincide con la recta de máxima inclinación y es, al mismo tiempo, una recta de punta.La frontal f coincide con la recta de máxima pendiente y es una recta vertical.h3α3= VMα2h2yyY’Y’≡ f2f3α1≡h1f1
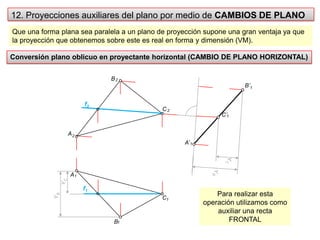
- 17. 12. Proyecciones auxiliares del plano por medio de CAMBIOS DE PLANOQue una forma plana sea paralela a un plano de proyección supone una gran ventaja ya que la proyección que obtenemos sobre este es real en forma y dimensión (VM). Conversión plano oblicuo en proyectante horizontal (CAMBIO DE PLANO HORIZONTAL)B2B’1f2C2C’1A2A’1A1YCPara realizar esta operación utilizamos como auxiliar una recta FRONTALf1YBYBC1YCB1
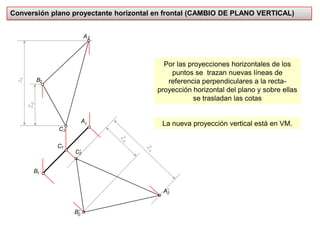
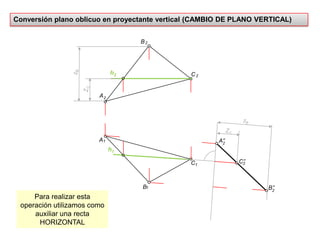
- 18. Conversión plano proyectante horizontal en frontal (CAMBIO DE PLANO VERTICAL)Por las proyecciones horizontales de los puntos se trazan nuevas líneas de referencia perpendiculares a la recta-proyección horizontal del plano y sobre ellas se trasladan las cotas1A1CLa nueva proyección vertical está en VM.21AC’B22CA’zAZA22BB’2ZBZB
- 19. Conversión plano oblicuo en proyectante vertical (CAMBIO DE PLANO VERTICAL)B2A”2C’’2h2C2B’’A22A1h1Para realizar esta operación utilizamos como auxiliar una recta HORIZONTALzBzBC1ZCZCB1
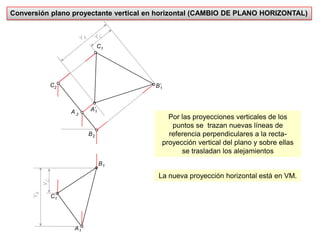
- 20. Conversión plano proyectante vertical en horizontal (CAMBIO DE PLANO HORIZONTAL)C1C2A2B’1B2A’1Por las proyecciones verticales de los puntos se trazan nuevas líneas de referencia perpendiculares a la recta-proyección vertical del plano y sobre ellas se trasladan los alejamientosB1YCYCCYBYB1La nueva proyección horizontal está en VM.A1
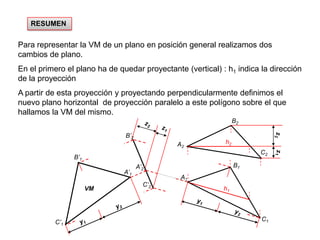
- 21. RESUMENPara representar la VM de un plano en posición general realizamos dos cambios de plano.En el primero el plano ha de quedar proyectante (vertical) : h1 indica la dirección de la proyecciónA partir de esta proyección y proyectando perpendicularmente definimos el nuevo plano horizontal de proyección paralelo a este polígono sobre el que hallamos la VM del mismo. B2B’1z2z2B’2h2A’1A2z1z1C2A’2B1A1C’2h1C’1y1y1y2y2C1VM
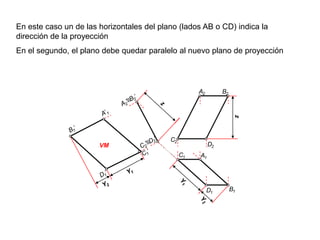
- 22. En este caso un de las horizontales del plano (lados AB o CD) indica la dirección de la proyecciónEn el segundo, el plano debe quedar paralelo al nuevo plano de proyecciónA2B2A2’≡B2’A’ 1zzC2B1’D2C1A1C2’≡D2’VMC1’Y1B1D1’D1Y1Y2Y2
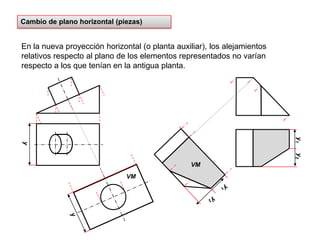
- 23. Cambio de plano horizontal (piezas)En la nueva proyección horizontal (o planta auxiliar), los alejamientos relativos respecto al plano de los elementos representados no varían respecto a los que tenían en la antigua planta.y1y1y2yyy2VMVM
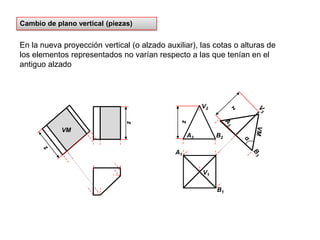
- 24. Cambio de plano vertical (piezas)En la nueva proyección vertical (o alzado auxiliar), las cotas o alturas de los elementos representados no varían respecto a las que tenían en el antiguo alzadoVMVMV2V3A3zzzA2B2αzA1B3V1B1
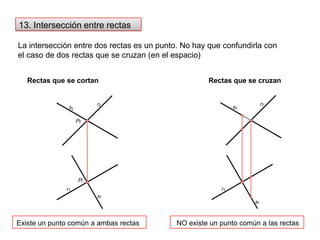
- 25. r2s2r2s2P2P1r1sr11s113. Intersección entre rectasLa intersección entre dos rectas es un punto. No hay que confundirla con el caso de dos rectas que se cruzan (en el espacio)Rectas que se cortanRectas que se cruzanExiste un punto común a ambas rectasNO existe un punto común a las rectas
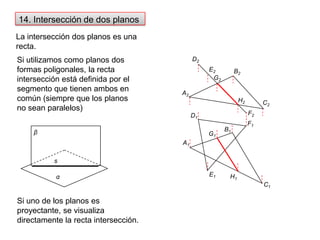
- 26. 14. Intersección de dos planosLa intersección dos planos es una recta. Si utilizamos como planos dos formas poligonales, la recta intersección está definida por el segmento que tienen ambos en común (siempre que los planos no sean paralelos)βD2B2E2sG2A2αC2H2F2D1F1B1G1A1E1H1C1Si uno de los planos es proyectante, se visualiza directamente la recta intersección.
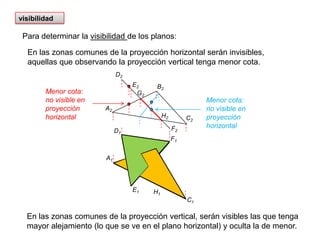
- 27. visibilidadPara determinar la visibilidad de los planos:En las zonas comunes de la proyección horizontal serán invisibles, aquellas que observando la proyección vertical tenga menor cota.D2B2E2G2Menor cota: no visible en proyección horizontalA2C2H2Menor cota: no visible en proyección horizontalF2D1F1B1G1A1E1H1C1En las zonas comunes de la proyección vertical, serán visibles las que tenga mayor alejamiento (lo que se ve en el plano horizontal) y oculta la de menor.
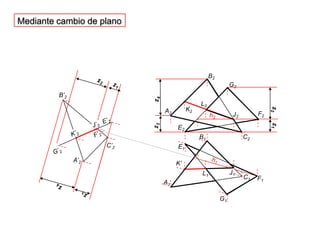
- 28. Mediante cambio de planoB2h2G2z4z4B’2z3z3z1z1L2z2z2K2J2F2J’2A2E’2K’h1K’2E2J1F’2C’2C2B1E1A’2G’2L1F1C1A1G1
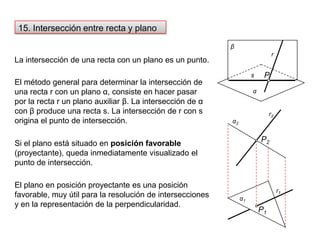
- 30. 15. Intersección entre recta y planoLa intersección de una recta con un plano es un punto. βrEl método general para determinar la intersección de una recta r con un plano α, consiste en hacer pasar por la recta r un plano auxiliar β. La intersección de α con β produce una recta s. La intersección de r con s origina el punto de intersección.Psαr2α2P2Si el plano está situado en posición favorable (proyectante), queda inmediatamente visualizado el punto de intersección.El plano en posición proyectante es una posición favorable, muy útil para la resolución de intersecciones y en la representación de la perpendicularidad.r1P1α1
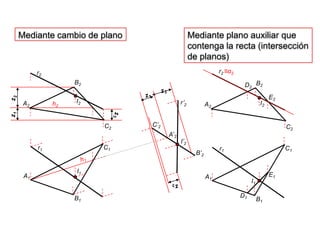
- 31. Mediante cambio de planoMediante plano auxiliar que contenga la recta (intersección de planos)r2r2≡α2D2B2B2h2r’2E2z1z1z2z2z3z3A2A2E1C’2A’2I1D1C2C2I’2r1r1I1I2I2B’2h1C1C1A1A1B1B1
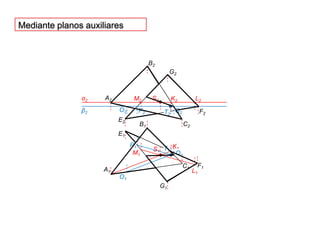
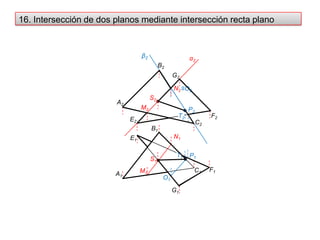
- 32. 16. Intersección de dos planos mediante intersección recta planoα2B2G2S2N2A2β2F2E2T2≡O2M2C2B1E1P2N1T1S1F1P1C1A1M1G1O1
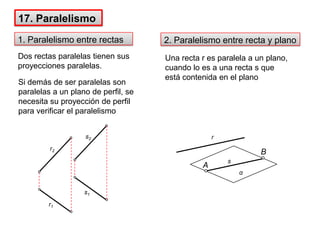
- 33. 17. Paralelismo1. Paralelismo entre rectas2. Paralelismo entre recta y planoDos rectas paralelas tienen sus proyecciones paralelas.Una recta r es paralela a un plano, cuando lo es a una recta s que está contenida en el planorr2s2Si demás de ser paralelas son paralelas a un plano de perfil, se necesita su proyección de perfil para verificar el paralelismoBAsαr1s1
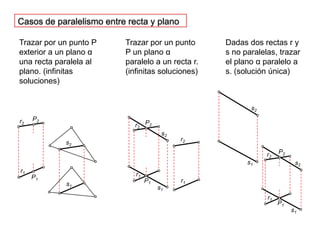
- 34. Casos de paralelismo entre recta y planoTrazar por un punto P exterior a un plano α una recta paralela al plano. (infinitas soluciones)Trazar por un punto P un plano α paralelo a un recta r. (infinitas soluciones)Dadas dos rectas r y s no paralelas, trazar el plano α paralelo a s. (solución única)P2P2P2s2r2r2r2r2s2s2s2P1P1P1s1r1r1r1r1s1s1s1
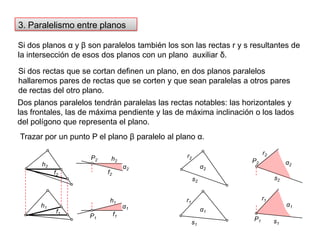
- 35. 3. Paralelismo entre planosSi dos planos α y β son paralelos también los son las rectas r y s resultantes de la intersección de esos dos planos con un plano auxiliar δ.P2P2Si dos rectas que se cortan definen un plano, en dos planos paralelos hallaremos pares de rectas que se corten y que sean paralelas a otros pares de rectas del otro plano.h2h2f2f2Dos planos paralelos tendrán paralelas las rectas notables: las horizontales y las frontales, las de máxima pendiente y las de máxima inclinación o los lados del polígono que representa el plano.P1P1h1h1f1Trazar por un punto P el plano β paralelo al plano α. f1r2r2α2α2α2s2s2r1r1α1α1α1s1s1
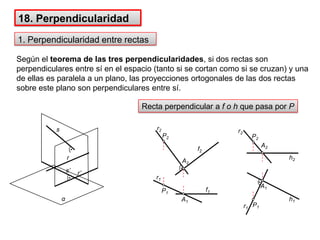
- 36. 18. Perpendicularidad1. Perpendicularidad entre rectasSegún el teorema de las tres perpendicularidades, si dos rectas son perpendiculares entre sí en el espacio (tanto si se cortan como si se cruzan) y una de ellas es paralela a un plano, las proyecciones ortogonales de las dos rectas sobre este plano son perpendiculares entre sí.A2A2P2P2rr2r1r2h2f2A1A1r1Recta perpendicular a f o h que pasa por P αP1ss’h1f1P1r’
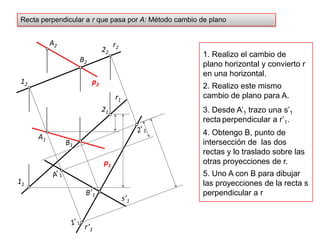
- 37. Recta perpendicular a r que pasa por A: Método cambio de plano12221. Realizo el cambio de plano horizontal y convierto r en una horizontal.B2A2p2r22. Realizo este mismo cambio de plano para A.r1213. Desde A’1 trazo una s’1 rectaperpendicular a r’1.A12’14. Obtengo B, punto de intersección de las dos rectas y lo traslado sobre las otras proyecciones de r.11p15. Uno A con B para dibujar las proyecciones de la recta s perpendicular a r B’1B1A’1s’11’1r’1
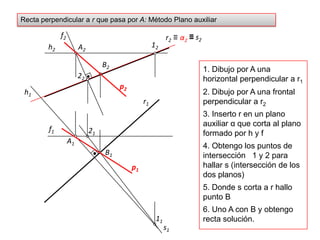
- 38. Recta perpendicular a r que pasa por A: Método Plano auxiliar B2f2≡ s212≡α222h2r2A2p21. Dibujo por A una horizontal perpendicular a r12. Dibujo por A una frontal perpendicular a r2r1h121B13. Inserto r en un plano auxiliar α que corta al plano formado por h y fA1f14. Obtengo los puntos de intersección 1 y 2 para hallar s (intersección de los dos planos)p15. Donde s corta a r hallo punto B6. Uno A con B y obtengo recta solución.11s1
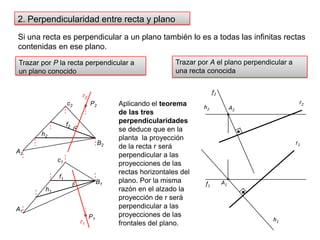
- 39. 2. Perpendicularidad entre recta y planof2P2Si una recta es perpendicular a un plano también lo es a todas las infinitas rectas contenidas en ese plano.h2r2Trazar por A el plano perpendicular a una recta conocidaTrazar por P la recta perpendicular a un plano conocidoA2f2h2c2r1r2Aplicando el teorema de las tres perpendicularidades se deduce que en la planta la proyección de la recta r será perpendicular a las proyecciones de las rectas horizontales del plano. Por la misma razón en el alzado la proyección de r será perpendicular a las proyecciones de las frontales del plano.A1f1B2f1A2h1c1P1B1h1A1r1
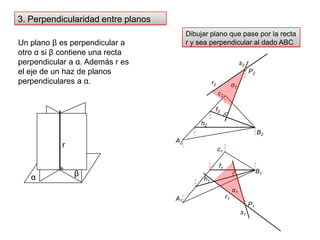
- 40. P23. Perpendicularidad entre planosDibujar plano que pase por la recta r y sea perpendicular al dado ABCUn plano βes perpendicular a otro αsi β contiene una recta perpendicular a α. Además r es el eje de un haz de planos perpendiculares a α.f2h2c2s2r2B2f1A2rh1c1P1α2B1βαA1r1s1α1
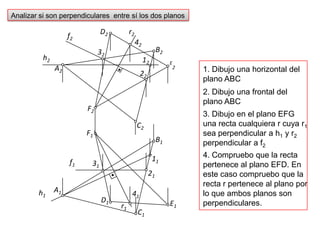
- 41. r242Analizar si son perpendiculares entre sí los dos planosf232D2h22212B21. Dibujo una horizontal del plano ABCE2A22. Dibujo una frontal del plano ABCF2C23. Dibujo en el plano EFG una recta cualquiera r cuya r1 sea perpendicular a h1 y r2 perpendicular a f2F1B141f1A1r14. Compruebo que la recta pertenece al plano EFD. En este caso compruebo que la recta r pertenece al plano por lo que ambos planos son perpendiculares.D11121E131C1h1