Semelhança de Triângulos, conceito com exemplos

Semelhança
de triângulos
Prof° Anderson
Roberto
Centro Educacional SESI – Dr Orlando Ometto
Ribeirão Preto/ SP

SEMELHANÇA DE TRIÂNGULOS
Usamos o símbolo ~ para indicar que dois
triângulos são semelhantes.
~

• VAMOS TRABALHAR??
Ampliando e reduzindo figuras simples:

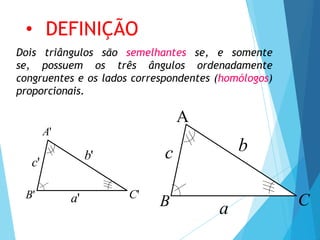
A'
C'
B'
c'
a'
b'
Dois triângulos são semelhantes se, e somente
se, possuem os três ângulos ordenadamente
congruentes e os lados correspondentes (homólogos)
proporcionais.
C
B
c
a
b
• DEFINIÇÃO
A

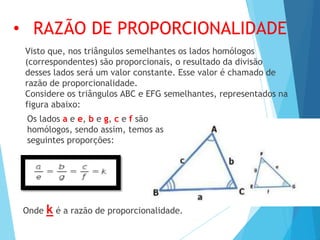
Visto que, nos triângulos semelhantes os lados homólogos
(correspondentes) são proporcionais, o resultado da divisão
desses lados será um valor constante. Esse valor é chamado de
razão de proporcionalidade.
Considere os triângulos ABC e EFG semelhantes, representados na
figura abaixo:
• RAZÃO DE PROPORCIONALIDADE
Os lados a e e, b e g, c e f são
homólogos, sendo assim, temos as
seguintes proporções:
Onde k é a razão de proporcionalidade.

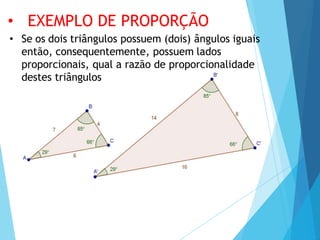
• Se os dois triângulos possuem (dois) ângulos iguais
então, consequentemente, possuem lados
proporcionais, qual a razão de proporcionalidade
destes triângulos
• EXEMPLO DE PROPORÇÃO

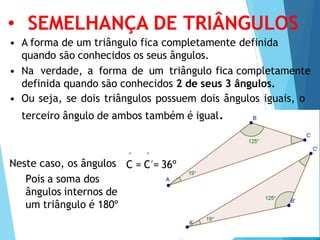
• SEMELHANÇA DE TRIÂNGULOS
• A forma de um triângulo fica completamente definida
quando são conhecidos os seus ângulos.
• Na verdade, a forma de um triângulo fica completamente
definida quando são conhecidos 2 de seus 3 ângulos.
• Ou seja, se dois triângulos possuem dois ângulos iguais, o
terceiro ângulo de ambos também é igual.
^ ^
Neste caso, os ângulos C = C´= 36º
Pois a soma dos
ângulos internos de
um triângulo é 180º

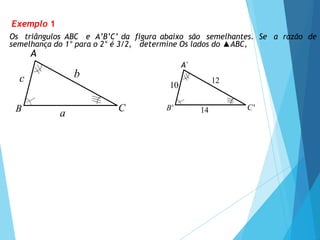
C'
B'
10
14
12
Exemplo 1
Os triângulos ABC e A’B’C’ da figura abaixo são semelhantes. Se a razão de
semelhança do 1° para o 2° é 3/2, determine Os lados do ▲ABC,
A
A'
C
B
c
a
b

C'
B'
10
14
12
Exemplo 1
Os triângulos ABC e A’B’C’ da figura abaixo são semelhantes. Se a razão de
semelhança do 1° para o 2° é 3/2, determine Os lados do ▲ABC,
A
A'
C
B
c
a
b
a

b

c

3
14 12 10 2
a

3
 a  21
 b 18
b

3
12 2
c

3
10 2
 c 15
14 2
 




:
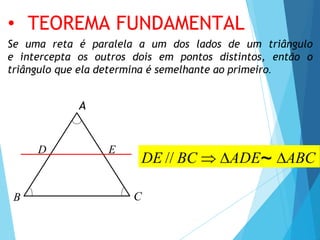
Se uma reta é paralela a um dos lados de um triângulo
e intercepta os outros dois em pontos distintos, então o
triângulo que ela determina é semelhante ao primeiro.
A
C
B
D E
DE // BC  ADE~ ABC
• TEOREMA FUNDAMENTAL

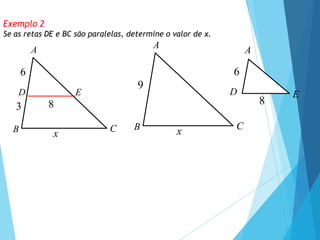
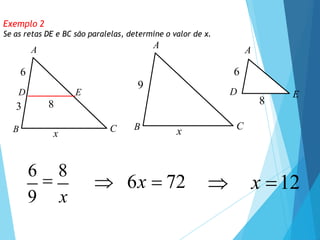
Exemplo 2
Se as retas DE e BC são paralelas, determine o valor de x.
A
C
B
3
6
D E
x
8
A
C
B
9
x
A
D E
6
8

Exemplo 2
Se as retas DE e BC são paralelas, determine o valor de x.
A
C
B
3
6
D E
x
8
A
C
B
9
x
A
D E
6
8
6

8
9 x
 6x  72  x 12

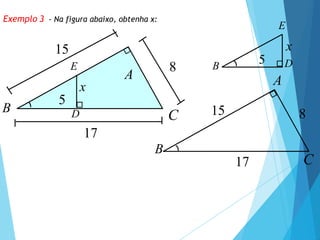
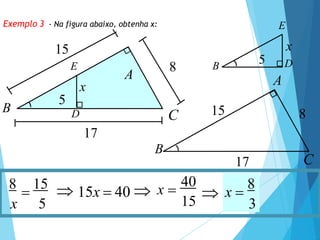
Exemplo 3 - Na figura abaixo, obtenha x:
x
8
15
17
A
C
B
5
D
E
8
15
17
A
C
B
B
E
x
D
5

Exemplo 3 - Na figura abaixo, obtenha x:
x
8
15
17
A
C
B
5
D
E
8
15
17
A
C
B
B
E
x
D
5
15
x 5 3
8

15  15x  40  x 
40
 x 
8

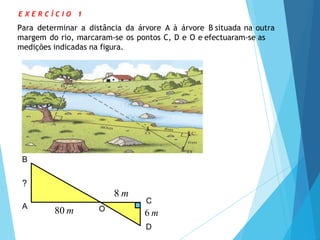
80 m
8 m
?
C
6 m
D
O
B
A
E X E R C Í C I O 1
Para determinar a distância da árvore A à árvore B situada na outra
margem do rio, marcaram-se os pontos C, D e O e efectuaram-se as
medições indicadas na figura.

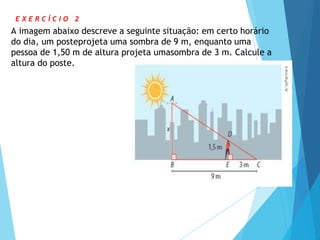
A imagem abaixo descreve a seguinte situação: em certo horário
do dia, um posteprojeta uma sombra de 9 m, enquanto uma
pessoa de 1,50 m de altura projeta umasombra de 3 m. Calcule a
altura do poste.

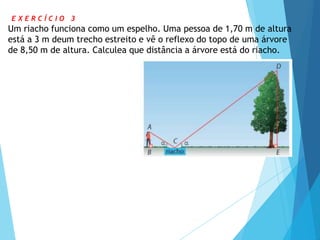
Um riacho funciona como um espelho. Uma pessoa de 1,70 m de altura
está a 3 m deum trecho estreito e vê o reflexo do topo de uma árvore
de 8,50 m de altura. Calculea que distância a árvore está do riacho.

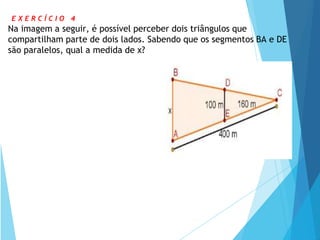
Na imagem a seguir, é possível perceber dois triângulos que
compartilham parte de dois lados. Sabendo que os segmentos BA e DE
são paralelos, qual a medida de x?

Semelhança de Triângulos, conceito com exemplos

Mais conteúdo relacionado

Mais procurados (20)

Semelhante a Semelhança de Triângulos, conceito com exemplos (20)

Último (20)

Semelhança de Triângulos, conceito com exemplos