Segmentos proporcionais 1
- 2. Agenda do dia 8h: Acolhida; 8h30min: Slide - Segmentos proporcionais Retângulo Áureo 10h: Intervalo; 10h20min: Vídeo olhando por outro ângulo e oficina construção de um transferidor. 11h20 min: Editora Ática 12h: Almoço; 13h: Oficina - Construção do Geoplano Atividades- ver material de apoio 16 h 30 min : Encerramento
- 6. Retângulo Áureo presente na arquitetura
- 7. Retângulo Áureo presente na pintura
- 8. Retângulo Áureo presente na natureza
- 9. 1. RAZÃO A razão de dois números a e b, com b 0, é o quociente do primeiro pelo segundo: OBSERVAÇÃO: A palavra razão vem do latim ratio, que significa divisão. Exemplos
- 10. 2. RAZÃO DE DOIS SEGMENTOS Chamamos razão de dois segmentos a razão ou quociente entre os números que exprimem as medidas desses segmentos, tomados na mesma unidade. Exemplos: Determinar a razão entre os segmentos AB e CD, sendo AB = 6 cm e CD = 12 cm.(Lembre-se :AB representa a medida do segmento AB.)
- 11. Exemplos: 1) Verifique se os segmentos AB =4 cm, CD = 6 cm, EF = 8 cm e GH = 12 cm formam, nessa ordem, uma proporção. Podemos afirmar que os segmentos, nessa ordem, são proporcionais.
- 12. 3. SEGMENTOS PROPORCIONAIS Dizemos que quatro segmentos, AB, CD, EF e GH, nessa ordem, são proporcionais, quando a razão entre os dois primeiros for igual à razão entre os dois últimos, ou seja: AB, CD, EF e GH são, nessa ordem, proporcionais se, e somente se:
- 13. 2) Verifique se os segmentos AB = 7 cm, CD = 10cm, EF = 12 cm e GH = 5 cm formam, nessa ordem, uma proporção. Podemos afirmar que os segmentos, nessa ordem, não são proporcionais.
- 14. 5x = 60 x= 12 3) Quatro segmentos AB, MN, PQ e RS, nesta ordem, são proporcionais. Se AB=5 cm, MN= 15 cm e PQ= 4 cm, qual a medida de RS?
- 15. A proporção aúrea na história
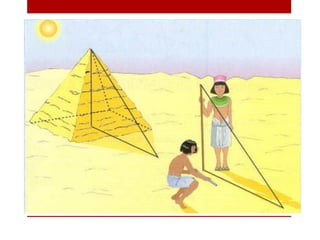
- 16. Tales de Mileto Conta a lenda que, por volta do ano 600 a. C., o filósofo Matemático grego Tales de Mileto (c. 624-547 a. C) fez uma viagem ao Egito. O faraó já conhecia sua fama de grande Matemático. Ouvira dizer que Tales era capaz de uma incrível façanha. Podia calcular a altura de uma construção, por maior que fosse, sem precisar subir nela.
- 17. Por ordem do monarca, alguns matemáticos egípcios foram ao encontro do visitante e pediram-lhe que calculasse a altura de uma pirâmide. Tales ouviu-os com atenção e dispõe a atendê-los imediatamente
- 18. Já no deserto próximo a pirâmide o sábio fincou no chão uma vara, na vertical. Observando a posição da sombra . Tales deitou a vara no chão, a partir do ponto em Que for fincada, marcou na areia o tamanho de seu comprimento. Depois voltou a Vara na posição vertical.
- 19. -Vamos esperar alguns instantes, disse ele. Daqui a pouco poderei dar a resposta. Ficaram todos ali, observando a sombra que a vara projetava. Num determinado momento, a sombra ficou exatamente do comprimento da vara. Tales disse então aos Egípcios: -Vão depressa até a pirâmide, meçam sua sombra e acrescente ao resultado a medida Da metade do lado da base. Essa soma é a medida exata da pirâmide.
- 20. Com apenas um bastão e aplicando o grande conhec imento que tinha sobre os segmentos , Tales venceu o desafio e com uma questão prática no momento em que a vara e sua sombra têm exatamente o mesmo tamanho, formam um triângulo retângulo isósceles , semelhantes a outro triângulo retângulo e isósceles formado pela pirâmide. e sua sombra. Assim, usando o conceito de semelhança de triângulos tales deduziu que a altura da pirâmide é igual a medida de sua sombra mais a metade da medida da base, Uma simples vara, duas sombras e uma magnífica idéia! ,
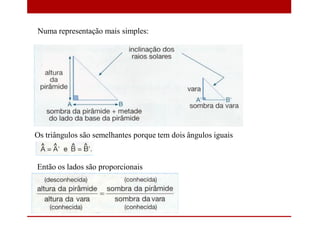
- 22. Numa representação mais simples: Os triângulos são semelhantes porque tem dois ângulos iguais Então os lados são proporcionais
- 24. Que tal você tentar resolver o problema abaixo usando a relação entre as alturas propostas por Tales 1) (Saresp) Um prédio projeta uma sombra de 40 m ao mesmo tempo que um poste de 2 m projeta uma sombra de 5 m. Então, a altura do prédio é A) 10 m. B) 12 m. C) 14 m. D) 16 m.
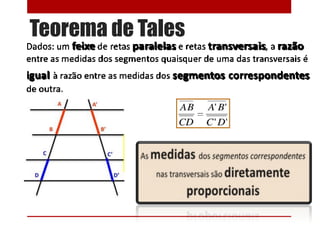
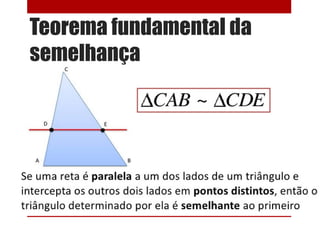
- 25. Teorema de Tales
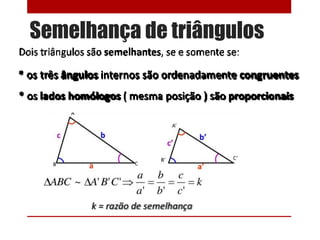
- 28. Casos (ou critérios) de semelhanças
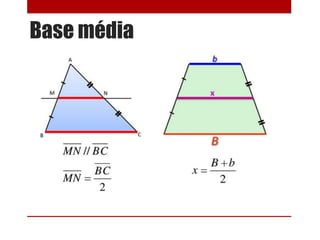
- 29. Base média