Ruffass Paulo Tequenha AULA 2 de GP (1).pptx
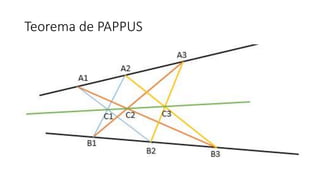
- 1. Breve Histórico Ideias iniciais A Geometria projetiva começa a fazer-se sentir, de forma tímida, com a ideia de Pappus (300 AC) que: Se três pontos A1, A2 e A3 são colineares e se B1, B2 e B3 são colineares, então os pontos C1, C2 e C3, resultantes da intersecção de (A1,B2)^(A2,B1), (A1,B3)^(A3,B1) e (A2,B3)^(A3,B2), respetivamente, também são colineares.
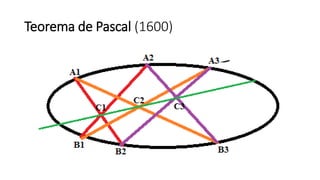
- 3. Generalização de Pascal (1600) Mais tarde, Pascal chegou as mesmas conclusões usando Cónicas (Circulo ou circunferência, elipse, parábola e hipérbole), ou seja: Teorema: Se três pontos A1, A2 e A3 são de um lado de uma cónica e se B1, B2 e B3 são do outro lado da mesma cónica, então os pontos C1, C2 e C3, resultantes da intersecção de (A1,B2)^(A2,B1), (A1,B3)^(A3,B1) e (A2,B3)^(A3,B2), respetivamente, também são colineares.
- 4. Teorema de Pascal (1600)
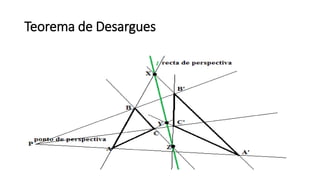
- 5. Gerard Desargues (1600) Gerard Desargues, começou seu contributo com a descoberta do teorema sobre perspetividade. Teorema: Se dois triângulos são perspetivos em relação a um ponto, também o são em relação a uma recta. Este teorema é basicamente a mesma conclusão encontrada por Pappus (pontos colineares) e Pascal (pontos de uma cónicas) que resultam em pontos colineares.
- 7. Renascimento artistico: Problema da perspectiva O interesse de representar as formas geométricas de modo que o olho vê, fez com que surgisse ou se necessitasse a noção do ponto no infinito, para o qual converge todas as linhas paralelas. De facto, objectos do mesmo tamanho tem tamanhos diferentes quando vistos a distancias diferentes, onde o mais próximo eh grande em relação ao mais distante.
- 8. Renascimento artistico: Problema da perspectiva
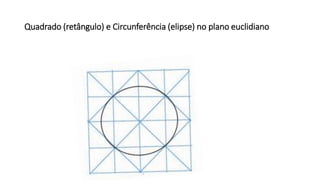
- 9. Quadrado (retângulo) e Circunferência (elipse) no plano euclidiano
- 10. Plano Projectivo A intenção de representar os elementos geométricos de modo real (como o olho vê), fez com que os Artistas e Desargues introduzisse a linha no infinito ou linha do horizonte, para onde todo o feixe de rectas paralelas converge num ponto (do infinito). Nota: O ponto do infinito situa-se na linha do horizonte
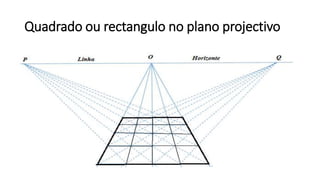
- 11. Quadrado ou rectangulo no plano projectivo
- 12. Resultados do problema da perspectiva Regra 1: Linhas paralelas se intersectam no horizonte (infinito); Regra 2: Linhas Rectas devem ser representadas por linhas rectas; Regra 3: A imagem de uma conica é uma conica
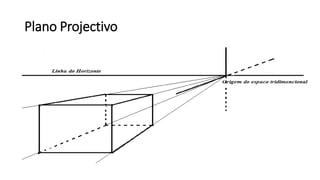
- 13. Plano Projectivo Ao conjunto do plano Euclidiano (usual), linha e ponto no horizonte (infinito), denomina-se de Plano Projectivo.
- 14. Plano Projectivo
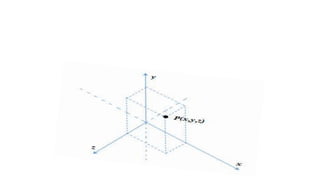
- 15. Outra Definição Plano Projectivo é o conjunto de todas as rectas que passa pela origem no espaço Euclidiano tridimensional. Cada recta que passa pela origem associamos um ponto projectivo