00Capítulo 2-conjuntos (1)
Transferir como PPT, PDF•1 gostou•505 visualizações
1. O documento descreve os conceitos fundamentais da teoria de conjuntos desenvolvida por Georg Cantor, incluindo conjuntos, elementos, relações de pertinência e operações entre conjuntos como união, intersecção e diferença. 2. A teoria de conjuntos é apresentada por meio de suas noções primitivas, formas de representação de conjuntos e operações entre conjuntos como união, intersecção e diferença. 3. Exemplos ilustram os principais conceitos como subconjuntos, conjunto das partes, cardinalidade e resolução de problemas envolvendo
00Capítulo 2-conjuntos (1)
- 2. Os resultados do trabalho de Georg Ferdinand Ludwing Phillip Cantor estabeleceram a teoria de conjuntos como uma disciplina matemática completamente desenvolvida e de profundos efeitos de ensino. Esta teoria baseia-se em três noções primitivas (noções que não podem ser definidas) que são: conjuntos, elementos e relação de pertinência.
- 3. 2.1. CONJUNTOS: Coleções, classes ou agrupamentos de objetos. Obs: devemos indicar um conjunto por uma letra maiúscula de nosso alfabeto (A, B, C, D, E, ...) 2.2. ELEMENTOS: é cada objeto de uma coleção. Obs: devemos indicar um elemento por uma letra minúscula de nosso alfabeto (a, b, c, d, e, ...) 2.3. RELAÇÃO DE PERTINÊNCIA: ∈ ∉ (Pertence) (Não pertence) Obs: Os símbolos ao lado, são usados para relacionar apenas elementos com conjuntos.
- 4. 3.1. Forma Tabular ou Enumerativa: Escrevemos os elementos entre chaves e separados por vírgulas. Exemplo: a) Conjunto V das vogais. V = {a, e, i, o ,u} (conjunto finito) b) Conjunto P dos números primos positivos. P = {2, 3, 5, 7, 11, ...} (conjunto infinito) c) Conjunto U dos números pares primos positivos. U = {2} d) Conjunto G das cores da bandeira brasileira que começam com a letra m. G = { }
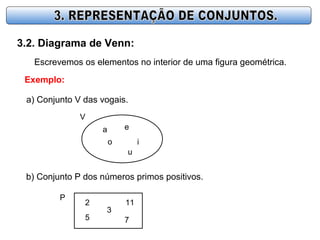
- 5. 3.2. Diagrama de Venn: Escrevemos os elementos no interior de uma figura geométrica. Exemplo: a) Conjunto V das vogais. V a e io u b) Conjunto P dos números primos positivos. P 2 3 7 11 5
- 6. 3.3. Propriedade Característica: Representamos o conjunto através de uma propriedade característica de seus elementos. Exemplo: a) Conjunto V das vogais. }{ vogaléxxV = },,,,{ uoiea= b) Conjunto P dos números primos positivos. }{ positivoprimonúmeroéxxP = ,...}11,7,5,3,2{= c) Conjunto U dos números pares primos positivos. }{ positivoprimoparnúmeroéxxU = }2{= d) Conjunto Solução S da equação do 1º grau 5x – 10 = 0. }0105{ =−∈= xRxS }2{=S
- 7. Dizemos que dois ou mais conjuntos são iguais se eles possuem os mes- mos elementos. Exemplo: }{ positivoprimoparnúmeroéxxU = }2{= }0105{ =−∈= xRxS }2{=S A repetição de elementos não altera um conjunto. Assim: {b, c, c, c, d, e, e} = {b, c, d, e} A ordem dos elementos não altera um conjunto. Assim: {g, o, l} = {l, o, g, o} e {f, i, a, t} = {f, a, t, i, a}
- 8. 5.1. Conjunto Unitário: É aquele que apresenta um único elemento. Exemplo: }0123{) =−∈= xRxVa }4{= }{) primoepositivoparnúmeroéxxUb = }2{= 5.2. Conjunto Vazio: É aquele que não apresenta elemento algum e é indicado por { } ou
- 9. Exemplo: }00{ <>∈= xexNxD }{= Um conjunto vazio sempre é dado por uma propriedade logicamente falsa. O conjunto { } representa um conjunto unitário e não um conjunto vazio.
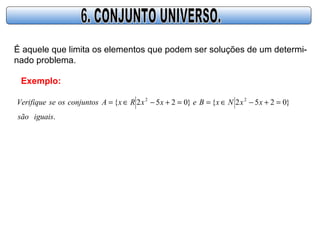
- 10. É aquele que limita os elementos que podem ser soluções de um determi- nado problema. Exemplo: . }0252{}0252{ 22 iguaissão xxNxBexxRxAconjuntososseVerifique =+−∈==+−∈=
- 11. Dados dois conjuntos A e B, dizemos que A é um subconjunto de B se, e somente se, para todo elemento x pertencente ao conjunto A, x pertence também a B. Podemos dizer a mesma coisa de quatro maneiras diferentes. A é subconjunto de B. A é parte de B. A está contido em B. BA ⊂ B contém A. AB ⊃
- 12. Exemplo: Escrever todos os subconjuntos do conjunto A = {0, 5, 7, 9}. -Subconjunto com nenhum elemento: -Subconjuntos com um elemento: {0}; {5}; {7}; {9} -Subconjuntos com dois elementos: {0,5}; {0,7}; {0,9}; {5,7}; {5,9}; {7;9} -Subconjuntos com três elementos: {0,5,7}; {0,5,9}; {0,7,9}; {5,7,9} -Subconjuntos com quatro elementos: {0,5,7,9} O número total de subconjuntos é igual a 16.
- 13. Conjunto das partes de um conjunto A, indicado por P(A), é aquele formado por todos subconjuntos que se pode formar a partir do conjunto A. Exemplo: Escrever o conjunto das partes de cada conjunto a seguir. a) B = {a, b, c}. b) F =
- 14. Sendo A = {{1}, {2}, {1,2}} podemos afirmar que: .}2{}1){( .2)( .}2{}1{)( .}1{)( .}1{)( AE AD AC AB AA ∈∪ ∈ ⊄∩ ⊂ ∉
- 16. 9.1. União: Dados dois conjuntos A e B chama-se união (ou reunião) entre A e B ao conjunto formado pelos elementos de A ou B. }{ BxouAxxBA ∈∈=∪ Exemplo: }8,7,6,4,2,0{=A }9,6,4,3{=B }9,8,7,6,4,3,2,0{=∪ BA
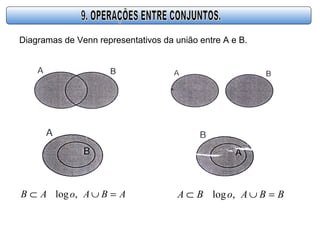
- 17. Diagramas de Venn representativos da união entre A e B. BBAoBA =∪⊂ ,logABAoAB =∪⊂ ,log
- 18. 9.2. Intersecção: Dados dois conjuntos A e B chama-se intersecção entre A e B ao conjunto formado pelos elementos comuns entre A e B, isto é, pelos elementos que Pertencem ao conjunto A e ao conjunto B. }{ BxeAxxBA ∈∈=∩ }8,7,6,4,2,0{=A }9,6,4,3{=B Exemplo: }6,4{=∩ BA
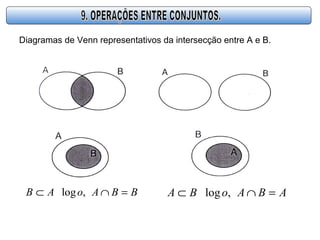
- 19. Diagramas de Venn representativos da intersecção entre A e B. ABAoBA =∩⊂ ,logBBAoAB =∩⊂ ,log
- 20. 9.3. Diferença: Dados dois conjuntos A e B chama-se diferença entre A e B ao conjunto formado pelos elementos do conjunto A que não pertencem ao conjunto B. }{ BxeAxxBA ∉∈=− Exemplo: }8,7,6,4,2,0{=A }9,6,4,3{=B }8,7,2,0{=− BA }9,3{=− AB }{ AxeBxxAB ∉∈=−
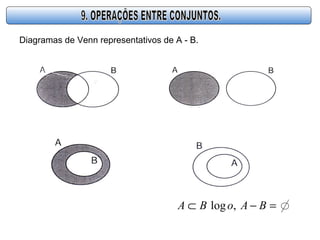
- 21. Diagramas de Venn representativos de A - B. =−⊂ BAoBA ,log
- 22. Diagramas de Venn representativos de B - A. =−⊂ ABoAB ,log
- 23. 9.3.1. Complementar: . , BAconuntoao AarelaçãoemBdearcomplementsechamaABquetaisBeAconjuntosdoisSejam − −⊂ ABseBAC B A ⊂−= , Exemplo: }8,7,6,4,2,0{=A }7,6,4{=B }8,2,0{=−= BAC B A
- 24. Exemplo: }9,7,5,3{=A }7,6,5{=B Como o conjunto B não está contido no conjunto A dizemos que o comple- mentar de B em relação a A não existe. . ., }.{:, ., BC BporAarelaçãoemBdearcomplementoindicarpodemosABSe CCvazioéarcomplementoBASe existenãoCarcomplementoquedizemosABSe B A B B A A B A = ⊂ === ⊄
- 25. Diagrama de Venn para B AC
- 26. 11.1. Cardinal de um Conjunto. 11.2. Fórmula para a Resolução de Problemas. )()()()( BAnBnAnBAn ∩−+=∪
- 27. 11.3. Problemas Envolvendo Conjuntos. Exemplos: As provas de recuperação em matemática e física de uma escola foram feitas no mesmo dia e durante a prova, observou-se a pre- sença de 42 alunos. Sabendo-se que 25 alunos fizeram a prova de matemática e 32 fizeram a de física, determine: a) O número de alunos que fizeram as duas provas; b) O número de alunos que fizeram apenas a prova de matemática; c) O número de alunos que fizeram apenas a prova de física.
- 28. Numa pesquisa sobre a qualidade dos serviços oferecidos pelas empresas de fornecimento de água (A), energia elétrica (E) e TV por assinatura (T) de um bairro, obteve-se um grande número de reclamações. A tabela a seguir expressa o número de reclamações de 300 entre- vistados durante a pesquisa. Com base na tabela, determine: a) O número de pessoas que não reclamaram de nenhum serviço; b) O número de entrevistados que reclamaram apenas do serviço oferecido pela empresa de fornecimento de água; c) O número de entrevistados que reclamaram de apenas um servi- ço; d) O número de entrevistados que reclamaram de pelo menos dois serviços.