Apostila matematica basica vol unico
- 2. .
- 3. Matemática Básica Volume único – Módulo 1 Dirce Uesu Pesco 5ª edição Roberto Geraldo Tavares Arnaut Apoio:
- 4. Fundação Cecierj / Consórcio Cederj Rua Visconde de Niterói, 1364 – Mangueira – Rio de Janeiro, RJ – CEP 20943-001 Tel.: (21) 2334-1569 Fax: (21) 2568-0725 Presidente Masako Oya Masuda Vice-presidente Mirian Crapez Coordenação do Curso de Matemática UFF - Regina Moreth UNIRIO - Luiz Pedro San Gil Jutuca Material Didático ELABORAÇÃO DE CONTEÚDO Departamento de Produção Dirce Uesu Pesco Roberto Geraldo Tavares Arnaut EDITORA PROGRAMAÇÃO VISUAL Tereza Queiroz Giuseppe Toscano COORDENAÇÃO DE DESENVOLVIMENTO Cristine Costa Barreto COORDENAÇÃO EDITORIAL CAPA Jane Castellani Eduardo Bordoni COORDENAÇÃO DE LINGUAGEM Maria Angélica Alves Sami Souza COORDENAÇÃO DE PRODUÇÃO PRODUÇÃO GRÁFICA Jorge Moura Fábio Rapello Alencar Copyright © 2005, Fundação Cecierj / Consórcio Cederj Nenhuma parte deste material poderá ser reproduzida, transmitida e gravada, por qualquer meio eletrônico, mecânico, por fotocópia e outros, sem a prévia autorização, por escrito, da Fundação. A745m Pesco, Dirce Uesu. Matemática básica. v. único / Dirce Uesu Pesco; Roberto Geraldo Tavares Arnaut. 5.ed. – Rio de Janeiro: Fundação CECIERJ, 2009. 324p.; 21 x 29,7 cm. ISBN: 978-85-7648-424-0 1. Fatoração. 2. Equação do 1° grau. 3. Equação do 2º grau. 4. Progressão aritmética. 5. Progressão geométrica. 6. Análise combinatória. I.Título. 2009/2 CDD: 510 Referências Bibliográficas e catalogação na fonte, de acordo com as normas da ABNT.
- 5. Governo do Estado do Rio de Janeiro Governador Sérgio Cabral Filho Secretário de Estado de Ciência e Tecnologia Alexandre Cardoso Universidades Consorciadas UENF - UNIVERSIDADE ESTADUAL DO UFRJ - UNIVERSIDADE FEDERAL DO NORTE FLUMINENSE DARCY RIBEIRO RIO DE JANEIRO Reitor: Almy Junior Cordeiro de Carvalho Reitor: Aloísio Teixeira UERJ - UNIVERSIDADE DO ESTADO DO UFRRJ - UNIVERSIDADE FEDERAL RURAL RIO DE JANEIRO DO RIO DE JANEIRO Reitor: Ricardo Vieiralves Reitor: Ricardo Motta Miranda UFF - UNIVERSIDADE FEDERAL FLUMINENSE UNIRIO - UNIVERSIDADE FEDERAL DO ESTADO Reitor: Roberto de Souza Salles DO RIO DE JANEIRO Reitora: Malvina Tania Tuttman
- 7. Matemática Básica Volume único – Módulo 1 SUMÁRIO Apresentação e Objetivos ____________________________________ 7 Aula 1 – Frações _____________________________________________ 11 Aula 2 – Números Decimais _____________________________________ 37 Aula 3 – Potenciação __________________________________________ 53 Aula 4 – Radiciação___________________________________________ 59 Aula 5 – Fatoração ___________________________________________ 69 Aula 6 – Equação do 1º grau ____________________________________ 77 Aula 7 – Sistema de Equações do 1º grau___________________________ 81 Aula 8 – Equação do 2º grau ____________________________________ 85 Aula 9 – Inequação do 1º grau___________________________________ 93 Aula 10 – Progressão Aritmética ________________________________ 103 Aula 11 – Progressão Geométrica _______________________________ 115 Aula 12 – Conjuntos _________________________________________ 129 Aula 13 – Introdução às Funções _______________________________ 141 Aula 14 – Funções Compostas e Inversa __________________________ 159 Aula 15 – Função do 1º grau___________________________________ 171 Aula 16 – Função Quadrática __________________________________ 183 Aula 17 – Função Modular ____________________________________ 195 Aula 18 – Função Exponencial _________________________________ 205 Aula 19 – Função Logaritmo ___________________________________ 215 Aula 20 – Trigonometria ______________________________________ 231 Aula 21 – Funções Trigonométricas ______________________________ 243 Aula 22 – Relações Fundamentais e Redução ao 1º Quadrante _________ 263 Aula 23 – Transformações_____________________________________ 277 Aula 24 – Equações Trigonométricas _____________________________ 291 Aula 25 – Funções Circulares Inversas ____________________________ 305 Aula 26 – Inequações Trigonométricas ___________________________ 313
- 9. Apresenta¸˜o e Objetivos ca Prezado(a) aluno(a), gostar´ıamos de dar boas-vindas nesta que pode ser considerada a primeira disciplina do seu Curso de Licenciatura em Ma- tem´tica da UFF/CEDERJ/UAB. Vocˆ est´ iniciando uma jornada que mu- a e a dar´ a sua vida. Vocˆ agora ´ parte de uma universidade p´blica, que lhe a e e u oferece a oportunidade de obter uma forma¸˜o de excelente qualidade. ca Estamos felizes por iniciar esta caminhada juntos em dire¸˜o a este ca t˜o nobre objetivo que ´ a forma¸˜o de quadros docentes com qualidade em a e ca nosso Estado, para atua¸˜o nos Ensinos Fundamental e M´dio. Para atingir ca e t˜o precioso objetivo, planejamos um curso aberto, com a maior flexibilidade a poss´ ıvel, e favorecendo o processo individual de constru¸˜o de sua autonomia. ca A proposta do curso ´ a forma¸˜o de qualidade diversificada, permitindo e ca planejar caminhadas futuras em P´s-gradua¸˜es, sem limites na escalada do o co processo de conhecimento, na perspectiva maior da educa¸ao autˆnoma, cujo c˜ o lema ´ aprender ao longo da vida. e Em todo o curso de Gradua¸˜o do CEDERJ, apoiado na metodologia ca da Educa¸˜o a Distˆncia, a orienta¸˜o de estudos ´ uma forte componente. ca a ca e Vocˆ, provavelmente, est´ cursando esta disciplina por orienta¸˜o da e a ca coordena¸˜o do curso, que ponderou oportuna uma recupera¸˜o de estudos ca ca centrada em conte´dos importantes de Matem´tica, pelos quais vocˆ passou u a e no Ensino M´dio. N˜o considere esta tarefa menor. Em nenhuma ´rea e a a do conhecimento os conte´dos est˜o t˜o encadeados e dependentes uns dos u a a outros como em Matem´tica. a Se construirmos um bom alicerce, o edif´ ser´ s´lido! ıcio a o Como in´ ıcio de percurso nesta boa jornada, teremos o tempo de cami- nhar e de descansar e tamb´m de enfrentar algumas ladeiras. Faz parte do e ´ jogo! E imposs´ chegar a lugares significativos, sem subir uma ladeira! ıvel Mas, uma vez no alto do morro, poderemos contemplar o horizonte que des- cortina a bela paisagem panorˆmica. a Como ter sucesso fazendo uma gradua¸˜o na modalidade a distˆncia? ca a Vocˆ j´ conhece as enormes vantagens que essa modalidade de ensino e a oferece e com certeza seu compromisso com o curso ´ grande. Sua forma¸˜o e ca inicia nesta disciplina com a constru¸˜o de uma s´lida base de conhecimentos ca o matem´ticos e com o desenvolvimento de h´bitos necess´rios para ter sucesso a a a na empreitada. Essa bagagem toda, adquirida nesta disciplina, lhe ser´ ex- a 7 CEDERJ
- 10. tremamente util, tanto na vida profissional quanto na vida pessoal. Mas ´ ´ e importante salientar algumas daquelas caracter´ ısticas t˜o necess´rias para se a a ter sucesso nessa forma de aprendizagem. Entre outras coisas pode-se mencionar a importˆncia de se ter for¸a a c de vontade, autodisciplina e dedica¸˜o. Organiza¸˜o tamb´m ´ fundamental. ca ca e e Vamos nomear algumas sugest˜es que ser˜o uteis: o a ´ ´ • Estude regularmente. E preciso que vocˆ fa¸a uma agenda de trabalho e c que lhe garanta um tempo espec´ıfico para o estudo. Isso significa que vocˆ n˜o pode estudar somente quando “tiver” tempo. Somos n´s os e a o respons´veis pelo nosso tempo. a • Consulte a tutoria para tirar d´vidas. A sua presen¸a `s se¸˜es de u c a co tutoria e a forma¸˜o de grupos de estudo s˜o ferramentas poderosas ca a que vocˆ disp˜e para progredir no curso. e o • Busque apoio na execu¸˜o das atividades propostas. A tutoria a distˆncia ca a tem um papel importante a cumprir no seu programa de estudos. Ela lhe dar´ uma maior agilidade para debelar d´vidas e isso ´ um privil´gio a u e e acess´ aos alunos do ensino a distˆncia. ıvel a • Estamos sempre trabalhando para que o material did´tico disponibili- a zado seja de qualidade e lhe dˆ um caminho seguro para a constru¸˜o e ca do seu conhecimento. • O trabalho semanal com os EPs, Exerc´ ıcios Programados, que ser˜oa disponibilizados todas as semanas, e a posterior an´lise dos correspon- a dentes gabaritos, o ajudar˜o a estar em dia com os estudos. Esse tra- a balho lhe permitir´ tra¸ar um mapa do curso, pelo qual vocˆ precisa a c e navegar. Ele lhe indicar´ os temas semanais que vocˆ precisa estudar, a e determinar´ os exerc´ a ıcios t´ ıpicos que vocˆ n˜o deve deixar de fazer, e a marcando um ritmo de estudo e progresso que vocˆ deve tentar manter. e Matem´tica, uma grande op¸˜o! a ca Vamos falar agora um pouco sobre Matem´tica, que j´ foi chamada a a “a rainha das ciˆncias”. e A Matem´tica desempenha um papel fundamental no desenvolvimento a cient´ıfico e tecnol´gico de nossa sociedade. Assim, maior ´ a nossa respon- o e sabilidade de contribuir para uma boa forma¸˜o nessa ´rea. ca a CEDERJ 8
- 11. H´ muita coisa a respeito da Matem´tica que a maioria das pessoas a a desconhece. O conhecimento delas pode mudar muito a nossa perspectiva dessa ciˆncia, sempre respeitada, mas nem sempre devidamente estimada. e E, como vocˆ sabe, a motiva¸˜o ´ fundamental para o aprendizado. e ca e No intuito de contribuir positivamente a esse respeito, ressaltamos al- guns pontos importantes para sua reflex˜o. a • A matem´tica n˜o lida apenas com n´meros, ela lida com n´meros, a a u u formas, rela¸˜es, argumenta¸˜es, enfim, lida com diversas id´ias e suas co co e inter-rela¸˜es. co • Estabelecer a verdade ´ o fim principal de qualquer tipo de ciˆncia. e e Chegar `quilo a que chamamos “verdade cient´ a ıfica”. Fundamental a respeito disso ´ a maneira como, no ˆmbito de cada atividade cient´ e a ıfica, se estabelece a verdade. Na Matem´tica, a “verdade” ´ estabelecida a partir de um conjunto de a e afirma¸˜es, chamadas de axiomas. Uma vez estabelecidas essas “verda- co des fundamentais”, usamos regras da l´gica para deduzir ou estabelecer o ´ todas as outras verdades. E o que chamamos “m´todo dedutivo”. Em e outras ciˆncias, a no¸˜o de verdade ´, em geral, estabelecida por expe- e ca e ´ rimentos. E por isso que, em muitos casos, uma nova teoria toma o lugar da anterior, que j´ n˜o consegue explicar os fenˆmenos que prevˆ a a o e ou em fun¸˜o do desenvolvimento de novas t´cnicas. Isso n˜o ocorre ca e a na Matem´tica, onde o conhecimento ´ sempre acumulativo. Esse fato a e distingue a Matem´tica das demais ciˆncias. a e • A principal atividade dos matem´ticos ´ resolver problemas. Podemos a e afirmar at´ que um matem´tico feliz ´ um matem´tico que acabou de e a e a resolver um bom problema e, ao fazer isso, descobriu mais uma por¸˜o ca de novos problemas para pensar. • Matem´tica tamb´m ´ sinˆnimo de diversidade. Em muitas l´ a e e o ınguas a palavra matem´tica ´ usada no plural. H´ tantas ramifica¸˜es e sub- a e a co a ´reas na matem´tica contemporˆnea que ´ imposs´ a a e ıvel acompanhar o desenvolvimento em todas as frentes de pesquisa. A matem´tica en- a contra inspira¸˜o para seu desenvolvimento nas mais diversas ´reas de ca a atua¸˜o humana. Uma boa id´ia pode surgir tanto em um problema mo- ca e tivado intrinsecamente na matem´tica como em uma situa¸ao pr´tica, a c˜ a ocorrida em algum campo fora dela. 9 CEDERJ
- 12. O que nos oferece a Matem´tica B´sica a a Nesta disciplina, Matem´tica B´sica, vocˆ ir´ rever alguns conceitos a a e a do Ensino Fundamental e M´dio. A diferen¸a aqui estar´ na forma da abor- e c a dagem que ser´ dada. Al´m de rever esses conceitos, de maneira efetiva, a e vocˆ construir´ uma atitude matem´tica profissional. A Matem´tica deixar´ e a a a a de ser um conjunto de regras e conven¸˜es e se desenvolver´ num conjunto co a sustentado de conhecimentos que se relacionam e se sustentam. Esperamos que ao final deste semestre vocˆ tenha sucesso e se sinta bastante confiante e para enfrentar os futuros desafios de seu curso. Para orientar seu estudo, a disciplina ´ apresentada em dois volumes, e cada um apresentando o conte´do program´tico sob a forma de aulas. Neste u a Volume I, que inicia a disciplina Matem´tica B´sica, revisaremos conte´dos a a u importantes do Ensino M´dio, entre as quais se destacam: Fra¸˜es, N´meros e co u Decimais, Potencia¸˜o, Radicia¸˜o, Equa¸˜es do Primeiro e Segundo Graus, ca ca co Inequa¸˜es, Progress˜es Aritm´tica e Geom´trica e Conjuntos. co o e e Elementos integrantes em todas as aulas s˜o os exemplos e as atividades a a serem resolvidas. Eles formam parte do conte´do e pontuam o encadea- u mento da disciplina. Assim, ´ importante que vocˆ entenda bem o desenvol- e e vimento dos exerc´ıcios e resolva todas as atividades. Bom estudo!! Conte sempre com nossa ajuda e nosso est´ ımulo. Sucesso! Roberto Geraldo Arnaut, Celso Costa, M´rio Olivero, Regina Moreth e Dirce Uesu Pesco. a CEDERJ 10
- 13. Fra¸oes c˜ ´ MODULO 1 - AULA 1 Aula 1 – Fra¸˜es co Os n´ meros est˜o no ˆmago de todas as coisas. u a a Pit´goras a Introdu¸˜o ca A Matem´tica, na forma como conhecemos hoje, teve seu in´ a ıcio no Per´ıodo de Ouro da Antiga Gr´cia. Parte primordial deste desenvolvimento e se deve a um grupo de matem´ticos que foi liderado por Pit´goras, autor de a a frases famosas, como a que abre essa aula. Os gregos foram particularmente felizes ao estruturar os conhecimentos matem´ticos desenvolvidos pelas civiliza¸˜es que os precederam, arrumando- a co os essencialmente nos moldes que praticamos at´ hoje. Eles tinham uma vis˜o e a predominantemente geom´trica desses conhecimentos, mas deram tamb´m os e e primeiros passos no estudo dos n´meros. A palavra Aritm´tica, por exemplo, u e ´ de origem grega. e Ao relermos a frase de Pit´goras mais uma vez, somos levados a conside- a rar a seguinte quest˜o: que tipo de n´ meros ele tinha em mente ao pronunciar a u frase t˜o lapidar? a A quest˜o procede, pois o conceito de n´ mero, como vemos hoje, de- a u morou muito tempo para se estabelecer e recebeu contribui¸˜es de muitas co culturas, por gera¸˜es e gera¸˜es de matem´ticos. co co a Por exemplo, os gregos n˜o tinham uma nota¸˜o espec´ a ca ıfica para repre- sentar os n´ meros, usavam letras, tais como os romanos depois deles. u A Matem´tica, assim como as ciˆncias em geral, n˜o teria se desenvol- a e a vido da maneira como observamos hoje sem a contribui¸˜o inestim´vel das ca a culturas hindu e ´rabe, que nos legaram os algarismos hindu-ar´bicos, assim a a como o sistema num´rico posicional. e N´ meros Naturais u Mas calma, voltemos um pouco, aos n´ meros tais como foram inici- u almente concebidos. Na forma mais primitiva, quando dizemos n´meros, u estamos nos referindo aos n´ meros chamados naturais, cujo conjunto repre- u sentamos pela letra N: N = { 1, 2, 3, 4, . . . } Os pontinhos indicam que podemos continuar assim, outro n´mero e u outro ainda, indefinidamente. Ou seja, o conjunto N ´ um manancial ines- e got´vel dessa mat´ria prima que usamos na confec¸˜o da Matem´tica. a e ca a 11 CEDERJ
- 14. Fra¸oes c˜ Preferimos n˜o incluir o zero nesse conjunto, uma vez que o zero, a n´ mero t˜o importante nas nossas vidas e na Matem´tica, custou bastante u a a para se estabelecer. A propriedade fundamental geradora dos N´ meros Naturais ´ a que u e cada um deles tem um sucessor. Essa no¸˜o ´ formalizada nos dois axiomas ca e conhecidos como Axiomas de Peano. O primeiro estabelece a existˆncia do e n´ mero natural 1 (afinal, ´ preciso come¸ar de alguma coisa) e o segundo u e c afirma que todo n´ mero natural tem um sucessor. Assim, come¸amos com u c 1, cujo sucessor ´ 2, seguido do 3, e assim por diante. e O que mais podemos fazer com os naturais? ´ E claro que a seq¨ˆncia de n´ meros naturais serve primordialmente ue u para contar coisas, tais como carneiros, frutas, flechas, dias e tudo o mais. Mas queremos mais do que isso. Veja, n˜o se deixe enganar pela simplicidade a desses n´ meros. u O que torna os n´ meros inteiros objetos matem´ticos de grande inte- u a resse ´ o fato de podermos operar com eles, somando-os e multiplicando-os. e Munido dessas duas opera¸˜es, o conjunto dos n´ meros naturais passa a apre- co u sentar quest˜es v´rias. Algumas delas continuam a desafiar mentes brilhantes o a at´ hoje. e Um teorema not´vel a Esse especial interesse matem´tico pelos n´ meros naturais ocorre es- a u pecialmente devido ` multiplica¸˜o. Nesse contexto surge um dos primeiros a ca resultados matem´ticos profundos com que tomamos contato. Do ponto de a vista da multiplica¸˜o, os n´ meros maiores do que 1 se dividem em duas ca u categorias: primos e compostos, dependendo de seus divisores. O teorema que mencionamos afirma que todo n´ mero natural, maior do que dois, se u decomp˜e em fatores primos e, mais ainda, a decomposi¸˜o ´ unica, a menos o ca e ´ da ordem dos fatores. Em linguagem informal, o teorema afirma que, do ponto de vista da multiplica¸˜o, todos os n´ meros podem ser montados a partir de ca u pe¸as b´sicas, os n´ meros primos, como um infinito brinquedo lego. Assim, c a u 6 = 2 × 3, 30 = 2 × 3 × 5, 121 = 112 , 660 = 22 × 3 × 5 × 11 e 47 = 47, pois 47 ´, ele pr´prio, um n´ mero primo. e o u Esse resultado matem´tico era conhecido pelos antigos gregos (vocˆ a e sabe o que ´ o crivo de Erat´stenes?) mas s´ foi rigorosamente demonstrado e o o 12 bem posteriormente, por Gauss, um dos maiores matem´ticos de todos os a CEDERJ
- 15. Fra¸oes c˜ ´ MODULO 1 - AULA 1 tempos. Seu nome cient´ ıfico ´ Teorema Fundamental da Aritm´tica. Mas, e e n˜o se preocupe com isso agora, haver´ tempo para ele no futuro. Mas, a a para que vocˆ n˜o fique apenas lendo, temos aqui duas atividades. Vocˆ e a e encontrar´ as solu¸˜es no fim da aula. a co Atividade 01 Explique de maneira convincente o porque dos n´ meros 1134 e 53172 u serem divis´ ıveis por 9. Atividade 02 Por que ´ dif´ decompor o n´ mero 97343 em fatores primos? e ıcil u Dois velhos conhecidos . . . Atrav´s da decomposi¸˜o em fatores primos podemos chegar a dois e ca importantes conceitos associados a dois n´ meros dados, digamos a e b: o u m´ınimo m´ltiplo comum, mmc(a, b), e o maior divisor comum, mdc(a, b). u Para que servem esses n´ meros? u Deve haver uma boa resposta para essa pergunta, uma vez que nos ensinam a determin´-los desde os primeiros passos na escola... Bem, eles a servem para efetuar certas opera¸˜es de maneira ´tima! co o Como calcul´-los? a Se sabemos a decomposi¸˜o em fatores primos dos n´ meros a e b, ´ ca u e muito f´cil: para o mmc basta tomar os fatores primos que comparecem em a pelo menos um dos dois n´ meros (levando em conta a maior potˆncia, caso u e ele compare¸a tanto em a como em b); para o mdc basta tomar os primos c que aparecem simultaneamente nos dois n´ meros (levando em conta a menor u potˆncia, caso ele compare¸a tanto em a como em b). Veja dois exemplos na e c tabela a seguir. a b mdc(a, b) mmc(a, b) 6=2×3 15 = 3 × 5 3 2 × 3 × 5 = 30 1050 = 2 × 3 × 52 × 7 3 280 = 2 × 5 × 7 70 = 2 × 5 × 7 4200 = 23 × 3 × 52 × 7 Como os antigos matem´ticos faziam? a Os antigos gregos j´ conheciam algoritmos para calcular o mdc e o mmc a de pares de n´ meros. A id´ia do algoritmo se baseia no seguinte fato: u e Se r ´ o resto quando a ´ dividido por b, ent˜o mdc(a, b) = mdc(b, r). e e a Assim, usando divis˜es sucessivas, chegamos ao mdc. Veja, por exem- o plo, como calculamos o maior divisor comum de 72 e 30. 13 CEDERJ
- 16. Fra¸oes c˜ Num diagrama de trˆs linhas, colocamos os n´ meros 72 e 30 na linha e u do meio. Ao alto de 30 colocamos a parte inteira da divis˜o (Algoritmo de a Euclides) de 72 por 30 e sob o 72 colocamos o resto desta divis˜o. a 2 72 30 12 No segundo passo, colocamos o resto da primeira divis˜o ao lado do 30 a e repetimos a opera¸˜o: ca 2 2 72 30 12 12 6 Como todo algoritmo, basta prosseguir repetindo os passos at´ . . . e 2 2 2 72 30 12 6 12 6 0 O que aconteceu de diferente nessa etapa do algoritmo? Vocˆ notou e que o resto desta vez ´ igual a zero. Bom, isso indica que chegamos ao fim e do processo e o n´ mero obtido nesta etapa, 6, ´ o mdc: mdc(72, 30) = 6. u e 3 2 Realmente, 72 = 2 × 3 e 30 = 2 × 3 × 5 e, portanto, mdc(72, 30) = 2 × 3. Pratique o algoritmo calculando mdc(450, 105). Agora, um algoritmo para o c´lculo do mmc. Ele lembra bastante a o conhecido algoritmo de decomposi¸˜o em fatores primos. A diferen¸a ´ ca c e que efetuamos a decomposi¸˜o dos dois n´ meros simultaneamente. Veja, na ca u pr´tica, o c´lculo de mmc(132, 124). a a 132 126 2 66 63 2 33 63 3 11 21 3 mmc(132, 126) = 22 × 32 × 7 × 11 = 2772 11 7 7 11 1 11 1 1 Vocˆ pode usar essa t´cnica para calcular o mmc de mais do que dois e e n´ meros. S´ para ter certeza, vocˆ n˜o gostaria de calcular mmc(297, 140, 90)? u o e a CEDERJ 14
- 17. Fra¸oes c˜ ´ MODULO 1 - AULA 1 Por que representamos os inteiros pela letra Z? Os n´ meros naturais n˜o nos permitem representar certas situa¸˜es im- u a co portantes, como as que envolvem perdas e preju´ ızos. Mais ainda, h´ situa¸˜es a co nas quais sentimos a necessidade de estender os n´ meros naturais a um con- u junto, digamos assim, mais completo. Por exemplo, a equa¸ao x + 5 = 3 c˜ n˜o tem solu¸˜o no conjunto dos n´ meros naturais. Assim, a Matem´tica a ca u a demanda o que chamamos conjunto dos n´meros inteiros: u Z = { . . . , −3, −2, −1, 0, 1, 2, 3, . . . }. Vocˆ sabe por que representamos os inteiros pela letra Z no lugar de e algo como I? Bem, como vocˆ deve saber, a Teoria de Conjuntos foi criada por Georg e Cantor, que falava alem˜o. A palavra para n´ meros em alem˜o ´ Zahlen. a u a e Atividade 03 Quais das seguintes equa¸˜es podem ser resolvidas no ˆmbito dos n´ meros co a u naturais? E no ˆmbito dos n´ meros inteiros? a u a) x + 2 = 7 c) 3x + 7 = 4 e) 2x + 5 = 7 b) x + 4 = 1 d) 2x + 4 = 8 f) 2x + 6 = 13 Os N´ meros Racionais u Como vocˆ deve ter notado, ao fazer a atividade anterior, h´ situa¸˜es e a co nas quais nem mesmo o conjunto dos inteiros permite considerar. Em con- trapartida aos n´ meros inteiros dever´ u ıamos considerar os n´ meros quebrados, u n˜o ´ mesmo? a e Realmente, h´ situa¸˜es tanto no ˆmbito da Matem´tica quanto no a co a a caso de situa¸˜es, digamos assim, do dia-a-dia, nas quais lan¸amos m˜o da co c a no¸˜o de propor¸˜o. Veja o exemplo a seguir. ca ca Exemplo 01 Na figura a seguir, determine o comprimento do segmento AB. B N˜o ´ preciso ser gˆnio para concluir que o a e e comprimento do segmento AB ´ 4 unida- e des de comprimento, pois o fato de que, em triˆngulos semelhantes, lados corres- a pondentes s˜o proporcionais. Assim, AB a 2 ´ 4 unidades de comprimento, pois 1 est´ e a O A para 2 assim como 2 est´ para 4. a 1 1 Essa essˆncia da propor¸˜o ´ que queremos registrar numericamente. e ca e 15 CEDERJ
- 18. Fra¸oes c˜ Exemplo 02 Desde os prim´rdios os cozinheiros, os construtores e tantos outros pro- o fissionais tˆm usado essa no¸˜o de propor¸˜o em seus afazeres. Algo como: e ca ca “cinco medidas de ´gua para duas medidas de arroz” ou “uma medida de a cimento para seis de areia”. Seguindo essa receita podemos variar a quanti- dade daquilo que queremos preparar, seja arroz para duas pessoas, seja arroz para uma fam´ de doze pessoas, contanto que mantenhamos a propor¸˜o ılia ca 5 : 2 (cinco por dois). O que ´ um n´mero racional? e u Tornando uma hist´ria longa mais curta, queremos nos referir nume- o ricamente a propor¸˜es tais como as que foram exemplificadas: 1 : 2, 5 : 2 co ou 1 : 6 e assim por diante. Isto ´, propor¸˜es nas quais comparamos dois e co n´ mero inteiros. Para isso, ´ claro, precisamos de dois n´ meros inteiros, a e u e u b, com a propriedade importante de que b = 0, e representamos a propor¸˜o ca a a : b pela nota¸˜o . ca b Tudo muito bem, com o seguinte cuidado: devemos levar em conta que, por exemplo, 1 : 2 e 2 : 4 representam a mesma propor¸˜o. Assim, na vers˜o ca a 1 2 num´rica, e s˜o iguais. e a 2 4 Ufa! Podemos ent˜o dizer que um n´ mero racional ´ representado por a u e a uma fra¸˜o do tipo , na qual a e b s˜o n´ meros inteiros com b = 0 e que ca a u b duas fra¸˜es representam o mesmo n´ mero se, e somente se, satisfazem a co u seguinte rela¸˜o de igualdade: ca a c = ⇐⇒ a · d = c · b. b d Assim, obtemos o conjunto representado por Q, como uma esp´cie de e n extens˜o dos inteiros. Ou seja, se estabelecermos que, se n ∈ Z, ent˜o n = , a a 1 temos Z ⊂ Q. Atividade 04 Use a defini¸˜o anterior de igualdade de n´ meros racionais para verificar ca u 3 −3 que = . −5 5 −a a a Assim, de um modo geral, = , que denotamos por − . b −b b Atividade 05 2 1 Determine o valor de x tal que = . x−1 3 CEDERJ 16
- 19. Fra¸oes c˜ ´ MODULO 1 - AULA 1 Nota¸˜o ca Dado um par de n´ meros inteiros a e b, com b = 0, obtemos o n´ mero u u a racional e chamamos a de numerador e b de denominador. A palavra b fra¸˜o tamb´m ´ usada, mas serve para contextos mais gerais, nos quais ca e e numeradores e denominadores s˜o outros objetos matem´ticos e n˜o apenas a a a π n´ meros inteiros. Por exemplo, vocˆ deve ter ouvido falar da fra¸˜o ou da u e ca √ 2 2 fra¸˜o ca . Mas, por enquanto, tomaremos o termo fra¸˜o por sinˆnimo de ca o 2 n´ mero racional. u Leitura de uma fra¸˜o ca Na tabela abaixo indicamos, para cada n´ mero de partes iguais em que u foi dividida a unidade, o nome de cada parte. N´ mero de u Nome de N´ mero de u Nome de partes cada parte partes cada parte 2 −→ meio 9 −→ nono 3 −→ ter¸o c 10 −→ d´cimo e Curiosidade 4 −→ quarto 11 −→ onze avos Os homens da idade da Pedra n˜o usavam fra¸oes. O con- a c˜ 5 −→ quinto 12 −→ doze avos ceito de fra¸ao tornou-se ne- c˜ 6 −→ sexto 13 −→ treze avos cess´rio com a evolu¸ao dos a c˜ conhecimentos. 7 −→ s´timo e 100 −→ cent´simoe Os antigos eg´ ıpcios tinham 8 −→ oitavo 1000 −→ mil´simoe uma nota¸ao especial de c˜ fra¸ao com numerador 1. A c˜ Para efetuar a leitura de uma fra¸˜o vocˆ deve ler o numerador e, em ca e 1 fra¸ao , por exemplo, era in- c˜ seguida, o nome de cada parte. Este ultimo depende do n´ mero de partes ´ u 3 dicada colocando-se sobre o em que foi dividida a unidade, isto ´, do denominador da fra¸˜o. e ca inteiro 3 um sinal oval alon- gado: ; os babilˆnios usa- o Exemplos: vam fra¸oes com denomina- c˜ 1 1 dores 60, 602 , 603 , etc; j´ os a lˆ-se “um meio” e lˆ-se “um quinze avos” e romanos usavam fra¸oes com c˜ 2 15 denominador 12. 3 7 A nossa maneira atual de re- lˆ-se “trˆs quintos” e e lˆ-se “sete d´cimos” e e 5 10 presentar fra¸ao, por meio de c˜ uma barra, surgiu no s´culo e 8 49 lˆ-se “oito onze avos” e lˆ-se “quarenta e nove cent´simos” e e XVI. 11 100 Exerc´ ıcios 1. Qual a fra¸˜o representada pela parte sombreada de cada figura? ca a) b) c) d) 17 CEDERJ
- 20. Fra¸oes c˜ 7 2. Jo˜o acertou a dos 15 problemas de uma prova. Responda: 15 a) quantos problemas ele acertou? b) quantos problemas ele errou? c) que fra¸˜o representa o n´ mero de problemas que ele errou? ca u 3. Uma estante ´ formada por 9 prateleiras. Se enchermos 3 prateleiras e de livros, que fra¸˜o da estante n˜o foi aproveitada? ca a 4. Escreva como vocˆ lˆ as fra¸˜es: e e co 3 2 11 27 51 a) b) c) d) e) 5 10 50 100 1000 5. Determine 2 1 3 5 a) de 20 b) de 40 c) de 32 d) de 14 5 4 4 7 1 6. Se de um n´ mero ´ 5, qual ´ esse n´ mero? u e e u 3 3 1 7. Se de um n´ mero ´ 30, quanto ´ desse n´ mero? u e e u 5 5 3 8. Uma escola tem 40 professores, dos quais s˜o mulheres. Determine a 8 o n´ mero de professoras dessa escola. u Gabarito 3 3 1 5 1. a) b) c) d) 4 5 2 9 8 2. a) 7 b) 8 c) 15 6 3. 9 4. a) trˆs quintos e b) dois d´cimos e c) onze cinq¨ enta avos u d) vinte e sete cent´simos e e) cinq¨ enta e um mil´simos u e 5. a) 8 b) 10 c) 24 d) 10 6. 15 7. 10 8. 15 CEDERJ 18
- 21. Fra¸oes c˜ ´ MODULO 1 - AULA 1 Tipos de Fra¸˜es co Observe os seguintes exemplos: 1o ) Tomamos uma unidade, dividimos em quatro partes iguais e tomamos uma delas. 1 4 1 Encontramos essa fra¸˜o ca em que o numerador ´ menor que o e 4 denominador. Fra¸˜es assim s˜o chamadas de fra¸˜es pr´prias. co a co o 2o ) Tomamos outras duas unidades, dividimos cada uma delas em quatro partes iguais e tomamos cinco delas. 5 4 5 Encontramos uma fra¸˜o ca em que o numerador ´ maior que o e 4 denominador. Fra¸˜es assim s˜o chamadas fra¸˜es impr´prias. co a co o 5 1 Note que ´ o mesmo que uma unidade inteira e mais da unidade. e 4 4 5 1 5 1 Por isso dizemos que ´ o mesmo que 1 inteiro e . Indicamos: = 1 + . e 4 4 4 4 1 1 Outra maneira de indicar 1 + ´ 1 . e 4 4 1 A forma 1 lˆ-se “um inteiro e um quarto”. e 4 1 A forma 1 , composta de uma parte inteira e outra fracion´ria, ´ cha- a e 4 5 mada forma mista para representar . 4 Podemos passar uma fra¸˜o impr´pria para a forma mista sem recorrer ca o a desenhos ou figuras. 19 CEDERJ
- 22. Fra¸oes c˜ 21 Exemplo: Passar para a forma mista. 6 21 Devemos descobrir quantas unidades inteiras est˜o contidas em a e 6 quantos sextos sobram depois da separa¸˜o dessas unidades. ca Descobrimos isso dividindo 21 por 6 21 6 21 3 3 → unidades inteiras contidas em 6 ↑ n´ mero de sextos u que sobram 21 3 Ent˜o a =3 . 6 6 Transformar um n´ mero misto em fra¸˜o impr´pria. u ca o Exemplos: 2 2 3 2 5 1) 1 =1+ = + = 3 3 3 3 3 3 3 5 5 3 10 3 13 2) 2 =1+1+ = + + = + = 5 5 5 5 5 5 5 5 1 4 4 4 4 4 1 20 1 21 3) 5 = + + + + + = + = 4 4 4 4 4 4 4 4 4 4 3o ) Tomamos duas unidades, dividimos cada uma delas em quatro partes iguais e tomamos as oito partes. 8 4 8 Encontramos uma fra¸˜o ca em que o numerador ´ m´ ltiplo do de- e u 4 8 nominador. Fra¸˜es assim s˜o chamadas fra¸˜es aparentes. Note que ´ o co a co e 4 mesmo que 2 unidades inteiras, isto ´, 2 inteiros. e 8 Indicamos: = 2 4 A fra¸˜o aparente ´ uma outra forma de representar o n´ mero natural 2. ca e u 3 4 5 23 , , , s˜o fra¸˜es aparentes que representam o n´ mero natural 1. a co u 3 4 5 23 CEDERJ 20
- 23. Fra¸oes c˜ ´ MODULO 1 - AULA 1 As fra¸˜es podem ser classificadas em trˆs categorias. co e * Fra¸˜es Pr´prias → s˜o aquelas em que o numerador ´ menor que o co o a e denominador * Fra¸˜es Impr´prias → s˜o aquelas em que o numerador ´ maior ou co o a e igual ao denominador. * Fra¸˜es Aparentes → s˜o as fra¸˜es impr´prias em que o numerador ´ co a co o e m´ ltiplo do denominador. u As fra¸˜es aparentes podem ser escritas na forma de n´ mero natural. co u As fra¸˜es impr´prias e n˜o aparentes podem ser escritas na forma mista. co o a Exerc´ ıcios 1. Classifique cada uma das fra¸˜es em pr´prias (P), impr´prias (I) ou co o o aparentes (A). 8 18 2 32 57 a) b) c) d) e) 4 1 13 5 2 2. Escreva na forma mista as seguintes fra¸˜es impr´prias: co o 3 8 13 31 57 a) b) c) d) e) 2 3 4 6 11 3. Transforme cada n´ mero misto em fra¸˜o impr´pria: u ca o 1 1 3 1 3 a) 3 b) 4 c) 1 d) 5 e) 6 4 3 5 2 8 4 4. Em uma cidade, dos 280 ve´ ıculos existentes s˜o autom´veis e os a o 5 demais s˜o caminh˜es. Quantos caminh˜es h´ nessa cidade? a o o a 3 5. Jos´ possui R$ 480,00 e isto equivale a de sua d´ e ıvida na lanchonete 4 de Manoel. Quanto Jos´ deve a lanchonete? e Gabarito 1. a) A b) A c) P d) I e) I 1 2 1 1 2 2. a) 1 b) 2 c) 3 d) 5 e) 5 2 3 4 6 11 13 13 8 11 51 3. a) b) c) d) e) 4 3 5 2 8 21 CEDERJ
- 24. Fra¸oes c˜ 4 4. Observe que se s˜o autom´veis e o restante s˜o caminh˜es ent˜o a o a o a 5 5 representamos todos os ve´ıculos por 5 5 4 1 A fra¸˜o que representa o n´ mero de caminh˜es ´ − = ca u o e 5 5 5 N´ mero total de ve´ u ıculos: 280 1 1 de 280 – n´ mero total de caminh˜es → 280 = 56 u o 5 5 3 5. Vamos representar a d´ ıvida de Jos´ por x. Logo, temos que e x = 480 4 Ent˜o a 3x = 4 · 480 = 1920 x = 1920 : 3 = 640 Portanto, Jos´ deve R$ 640,00 a lanchonete. e Fra¸˜es Equivalentes co Note estas a¸˜es: co A¸˜o 1 ca A¸˜o 2 ca A¸˜o 3 ca Dividir uma pizza em Dividir uma pizza em Dividir uma pizza em duas partes iguais e quatro partes iguais e oito partes iguais e comer comer uma parte comer duas partes quatro partes iguais As a¸˜es acima s˜o diferentes, entretanto, as fra¸˜es obtidas represen- co a co tam a mesma parte do todo. Por esse motivo, dizemos que essas fra¸˜es se co 1 2 4 equivalem, isto ´, as fra¸˜es , e co e s˜o equivalentes. a 2 4 8 Fra¸˜es equivalentes s˜o fra¸˜es que representam a mesma parte do todo. co a co Obten¸˜o de fra¸˜es equivalentes ca co 1 Vamos obter fra¸˜es equivalentes ` fra¸˜o co a ca ? 3 1·1 1 1·2 2 1·3 3 1·4 4 = = = = 3·1 3 3·2 6 3·3 9 3·4 12 1 2 3 4 1 Assim, , , , s˜o algumas das fra¸˜es equivalentes a . a co 3 6 9 12 3 CEDERJ 22
- 25. Fra¸oes c˜ ´ MODULO 1 - AULA 1 Para encontrar essas fra¸˜es equivalentes, multiplicamos o numerador co 1 e o denominador da fra¸˜o por uma mesmo n´ mero natural diferente de ca u 3 zero. a Note que para obter uma fra¸˜o equivalente ` fra¸˜o (b = 0) basta ca a ca b dividir (se poss´ ıvel) ou multiplicar o numerador e o denominador por um mesmo n´ mero natural, desde que ele seja diferente de zero. u Simplifica¸˜o de fra¸˜es ca co 6 1 1 Uma fra¸˜o equivalente a ca ´ . A fra¸˜o foi obtida dividindo-se e ca 12 2 2 6 ambos os termos da fra¸˜o ca por 6. 12 1 6 Dizemos que a fra¸˜o ´ uma fra¸˜o simplificada de ca e ca 2 12 Uma fra¸˜o que n˜o pode ser simplificada ´ chamada de irredut´ ca a e ıvel. 1 Por exemplo, a fra¸˜o n˜o pode ser simplificada, porque 1 e 2 n˜o pos- ca a a 2 1 suem fator comum (mdc(1,2)=1). Podemos dizer, ent˜o, que ´ a fra¸˜o a e ca 2 6 irredut´ de ıvel . 12 Exerc´ ıcios 1 1. Quais das fra¸˜es s˜o equivalentes a co a ? 5 2 3 4 5 7 12 a) b) c) d) e) f) 10 12 18 25 30 60 2. Quais das fra¸˜es abaixo s˜o irredut´ co a ıveis? 1 7 15 24 12 a) b) c) d) e) 3 8 45 36 60 3. Encontre a fra¸˜o de denominador 20 equivalente a cada uma das se- ca guintes fra¸˜es: co 1 3 a) c) 5 2 1 400 b) d) 4 2000 4. As letras abaixo representam n´ meros. Quais s˜o esses n´ meros? u a u 4 a b 32 2 c a) = b) = c) = 6 18 5 20 5 50 23 CEDERJ
- 26. Fra¸oes c˜ Gabarito 1. a, d, f 2. a,b 4 5 30 4 3. a) b) c) d) 20 20 20 20 4. a) a = 12 b) b = 8 c)c = 20 Redu¸˜o de fra¸˜es a um mesmo denominador ca co 4 4 1 Observe as fra¸˜es , e . Elas tˆm denominadores diferentes. Vamos co e 3 5 6 procurar trˆs fra¸˜es, equivalentes `s trˆs fra¸˜es dadas, tendo todas o mesmo e co a e co denominador. O novo denominador ´ m´ ltiplo de 3, 5 e 6. O menor n´ mero e u u ´ o mmc(3,5,6) que ´ 30. e e 4 4 Estamos, ent˜o, com o problema - obter fra¸˜es equivalentes a , e a co 3 5 1 tendo todas elas denominador 30. 6 4 ? 4 40 = ⇒ o numerador ´ 4 · 10 = 40 ⇒ e = 3 30 3 30 4 ? 4 24 = ⇒ o numerador ´ 4 · 6 = 24 ⇒ e = 5 30 5 30 1 ? 1 5 = ⇒ o numerador ´ 1 · 5 = 5 e ⇒ = 6 30 6 30 Para reduzirmos duas ou mais fra¸˜es ao menor denominador comum: co 1o ) Calculamos o mmc dos denominadores, esse mmc ser´ o menor denomi- a nador comum; 2o ) Multiplicamos o numerador de cada fra¸˜o pelo quociente entre o deno- ca minador comum e o denominador inicial da fra¸˜o. ca Exerc´ ıcios 1. Reduza ao mesmo denominador comum. 3 5 12 3 a) e b) e 2 3 5 11 2 1 7 2 1 5 c) , e d) , e 5 3 6 7 6 9 2. Jo˜o e Maria v˜o repartir entre si um prˆmio da Loteria Federal. Jo˜o a a e a 2 ir´ receber do prˆmio e Maria R$ 1.500.000,00. Qual o valor total a e 5 do prˆmio? e CEDERJ 24
- 27. Fra¸oes c˜ ´ MODULO 1 - AULA 1 Gabarito 9 10 132 15 12 10 35 36 21 70 1. a) e b) e c) , e d) , e 6 6 55 55 30 30 30 126 126 126 2. A fra¸˜o que representa o valor do prˆmio que ser´ recebido por Maria ca e a 5 2 3 ´ − = do total. Como ela ir´ receber R$ 1.500.000,00, ent˜o o e a a 5 5 5 3 valor total do prˆmio (x) pode ser determinado por x = 1.500.000, 00. e 5 Da´ı, 3x = 5 · 1.500.000, 00 = 7.500.000, 00 x = 7.500.000, 00 : 3 = 2.500.000, 00 Compara¸˜o de Fra¸˜es ca co Comparar duas fra¸˜es significa estabelecer se elas s˜o iguais, ou n˜o. co a a Se forem diferentes, estabelecer qual delas ´ a maior. e 1a Situa¸˜o: As fra¸˜es tˆm denominadores iguais. ca co e 2 4 Exemplo: e 5 5 2 2 4 Usamos o s´ ımbolo “<” que 5 ´ menor que e significa “´ menor que” e o e 5 5 s´ ımbolo “>” que significa “´ e 2 4 maior que” 4 < 5 5 5 Quando duas fra¸˜es tem denominadores iguais, a maior delas ´ a que co e tem maior numerador. 2a Situa¸˜o: As fra¸˜es tˆm denominadores diferentes. ca co e 6 4 Vamos comparar as fra¸˜es co e . 7 5 Vamos reduzir as fra¸˜es ao mesmo denominador. mmc(7,5)=35 co 30 28 e 35 35 30 28 6 4 Da´ como ı > temos que > . 35 35 7 5 Quando vamos comparar duas fra¸˜es que tˆm denominadores diferentes, co e reduzimos ao mesmo denominador e aplicamos a regra anterior. 25 CEDERJ
- 28. Fra¸oes c˜ Exerc´ ıcios 1. Compare entre si as fra¸˜es: co 7 1 1 1 2 3 3 5 41 43 a) e b) e c) e d) 2 e2 e) e 5 5 6 13 5 7 6 7 13 15 9 3 7 2. Qual o maior elemento do conjunto A = , , , 2 5 4 3 3 4 5 1 1 3. Coloque em ordem crescente as fra¸˜es: co , , , e 5 7 8 2 4 2 7 4. Em certa classe, dos alunos foram reprovados em Matem´tica e a 5 9 em Portuguˆs. Que mat´ria reprovou mais? e e 5 5. Num campeonato nacional o Fluminense ganhou dos pontos que 7 11 disputou, enquanto o Vasco ganhou . Qual dos dois obteve melhores 16 resultados? Gabarito 7 1 1 1 3 2 3 5 41 43 1. a) > b) > c) > d) 2 <2 e) > 5 5 6 13 7 5 6 7 13 15 7 2. 3 1 1 4 3 5 3. , , , , 4 2 7 5 8 2 18 7 35 35 18 4. Portuguˆs, pois mmc(5, 9) = 45, e = e = e > 5 45 9 45 45 45 5 80 11 77 80 77 5. Fluminense, pois mmc(7, 16) = 112, = e = e > 7 112 16 112 112 112 Adi¸˜o e subtra¸˜o de n´ meros fracion´rios ca ca u a 1o Caso: Denominadores iguais 3 1 No mercado gastei do que possuia em alimentos e em material de 5 5 limpeza. Quanto gastei da importˆncia que possuia? a Vamos representar graficamente. gasto em alimentos gasto com material de limpeza 3 1 5 5 3 1 4 Da´ + = (s´ observar o gr´fico) ı o a 26 5 5 5 CEDERJ
- 29. Fra¸oes c˜ ´ MODULO 1 - AULA 1 A soma de fra¸˜es com denominadores iguais ´ uma fra¸˜o cujo denomi- co e ca nador ´ igual ao das parcelas e cujo numerador ´ a soma dos numeradores e e das parcelas. 4 1 No mercado gastei do que possuia em alimentos e em material de 6 6 limpeza. Quanto gastei a mais em alimentos? Vamos representar graficamente. gasto com gasto com material 4 1 alimentos: de limpeza: 6 6 Observando o gr´fico vem: a 4 1 3 − = 6 6 6 A diferen¸a entre duas fra¸˜es com denominadores iguais ´ uma fra¸˜o c co e ca cujo denominador ´ igual ao das fra¸˜es dadas e cujo numerador ´ a e co e diferen¸a dos numeradores. c 2o Caso: Denominadores diferentes Quando as fra¸˜es tem denominadores diferentes temos que, em pri- co meiro lugar, obter fra¸˜es equivalentes que tenham denominadores iguais. co 4 5 Exemplo: + 10 6 4 8 12 16 20 24 4 , , , , , . . . s˜o fra¸˜es equivalentes a a co . 10 20 30 40 50 60 10 5 10 15 20 25 30 35 40 45 50 5 , , , , , , , , , . . . s˜o fra¸˜es equivalentes a . a co 6 12 18 24 30 36 42 48 54 60 6 Procurando as fra¸˜es equivalentes que tem o mesmo denominador e co usando a regra anterior vem: 12 25 37 24 50 74 37 + = ou + = = 30 30 30 60 60 60 30 Note que mmc(10,6)=30. Devemos, usando o mmc, determinar a fra¸˜o ca equivalente com denominador 30. Quando vamos somar ou subtrair fra¸˜es que tem denominadores di- co ferentes, devemos primeiro reduz´ ı-las ao mesmo denominador e, depois, aplicar a regra anterior. 27 CEDERJ
- 30. Fra¸oes c˜ Exerc´ ıcios 1. Calcule: 3 1 5 2 3 a) + c) 3 − e) 4 +6 4 4 6 7 7 13 5 1 2 1 b) − d) 2 + + f) 5 − 4 4 4 4 4 9 2. Calcule: 1 1 1 4 2 6 3 a) + c) + + e) + 3 4 5 3 9 5 4 4 3 11 13 3 1 b) − d) + f) − 3 4 60 72 7 3 3. Calcule o valor de cada express˜o abaixo: a 4 1 5 1 a) − + − 3 5 4 3 1 1 4 1 b) 1 + − − − 3 5 3 2 1 1 1 c) 3 + 2 − 4 4 2 6 1 1 7 1 1 d) 3 −1 + 2 − − 2 −2 11 4 4 2 3 1 1 4. No s´ de Daniel, da planta¸˜o ´ de milho, ´ de feij˜o e o restante ıtio ca e e a 3 5 ´ de arroz. Qual ´ a fra¸˜o correspondente ` planta¸˜o de arroz? e e ca a ca 11 5. O censo revelou que, do total da popula¸˜o brasileira, ca s˜o brancos, a 20 10 s˜o morenos e negros e a fra¸˜o restante ´ de ra¸a amarela. a ca e c 25 Qual a fra¸˜o da popula¸˜o brasileira corresponde ` ra¸a amarela? ca ca a c Gabarito 13 11 75 8 1. a) 1 b) 2 c) d) e) f) 6 4 7 9 7 7 79 131 39 2 2. a) b) c) d) e) f) 12 12 45 360 20 21 123 9 19 80 3. a) b) c) d) 60 30 12 33 CEDERJ 28
- 31. Fra¸oes c˜ ´ MODULO 1 - AULA 1 1 1 5 3 8 4. + = + = . 3 5 15 15 15 15 15 8 7 A planta¸˜o inteira corresponde a ca logo, temos de arroz − = 15 15 15 15 5 5. 100 Multiplica¸˜o e divis˜o de n´ meros fracion´rios ca a u a Multiplica¸˜o ca Jo˜o tem um terreno quadrado de lados medindo 1 km. Ele precisa a cercar uma parte desse terreno para o pasto de seu gado. Para isso, vai usar 3 3 de um lado e do outro. Que fra¸˜o do terreno ser´ o pasto? Qual ser´ ca a a 4 5 a ´rea desse pasto? a 3 3 Como v˜o ser usados de um lado e do a 4 5 9 outro, o pasto ser´ a do terreno. (Observe 20 o gr´fico) a Mas o terreno ´ quadrado e a ´rea de um quadrado ´: A = 1 km · 1 km = e a e 2 1 km . 9 9 Como o pasto ´ igual a e do terreno, sua ´rea ´ a e de 1 km2 , ou 20 20 9 seja, km2 . Assim, a ´rea do pasto, que ´ um retˆngulo, pode ser obtida a e a 20 aplicando a f´rmula: Aretˆngulo = b · h onde b → base e h → altura. o a 3 3 3 3 9 Da´ Aretˆngulo = ı a · km2 . Temos que · = . 4 5 4 5 20 Portanto para multiplicar duas fra¸˜es, basta multiplicar os numerado- co res entre si e os denominadores entre si. Exemplos: 3 5 3·5 15 5 3 7 21 1) · = = = 2) · = =1 4 6 4·6 24 8 7 3 21 Observa¸˜o: Podemos evitar a simplifica¸˜o do produto de fra¸˜es se tomar- ca ca co mos o cuidado de cancelar os fatores comuns ao numerador e denominador das fra¸˜es que v˜o ser multiplicadas. co a Exemplos: 8 4 40 32 1) · = 1 7 5 7 1 105 50 3 5 2) · = 12 2 5 1 42 29 CEDERJ
- 32. Fra¸oes c˜ Exerc´ ıcios 1. Calcule 1 a) O triplo de 7 4 b) A metade de 5 c) A ter¸a parte de 18 c 4 11 d) Os de 7 5 2. Calcule os produtos 1 4 2 3 a) · c) · 3 3 3 8 2 3 1 b) · d) 9 · 7 5 9 3. Calcule o valor das express˜es: o 1 3 1 3 a) · + · 2 5 6 4 3 5 8 7 b) + · − 5 3 7 8 1 5 2 5 2 c) 1 + · − · − 2 4 3 2 5 18 1 24 5 7 d) · + · · −1 35 5 15 49 3 2 2 4. Jos´ comeu e de uma barra de chocolate e Jo˜o comeu do restante. a 5 3 a) Quem comeu mais? b) Que fra¸˜o do chocolate sobrou? ca Gabarito 3 2 44 1. a) b) c) 6 d) 7 5 35 4 6 1 2. a) b) c) d) 1 9 35 4 17 17 9 2136 3. a) b) c) d) 40 28 40 8575 4. a) Os dois comeram a mesma quantidade de chocolate, pois Jos´ comeu e 2 2 5 2 3 2 3 2 e Jo˜o comeu do restante a − = que significa de = . 5 3 5 5 5 3 5 5 2 2 4 5 4 1 b) Jos´ e Jo˜o comeram + = e sobrou − = . e a 5 5 5 5 5 5 CEDERJ 30
- 33. Fra¸oes c˜ ´ MODULO 1 - AULA 1 Divis˜o a Inverso ou rec´ ıproco 3 4 Chama-se inverso ou rec´ ıproco da fra¸˜o ca a fra¸˜o , isto ´, a fra¸˜o ca e ca 4 3 3 que se obt´m trocando entre si o numerador e o denominador de . e 4 3 4 12 Note que · = =1 4 3 12 Inverso ou rec´ ıproco de uma fra¸˜o diferente de zero ´ a fra¸˜o que se ca e ca obt´m trocando entre si o numerador e o denominador da fra¸˜o dada. e ca O produto de uma fra¸˜o pelo seu inverso ´ 1. ca e Quociente de fra¸˜es co 3 5 Vamos calcular o quociente : . 4 6 x Denominemos o quociente procurado pela fra¸˜o . ca y Temos: x 3 5 = : y 4 6 Multiplicando o quociente pelo divisor, obtemos o dividendo: x 5 3 · = y 6 4 5 Vamos multiplicar os dois membros dessa igualdade pelo inverso de , 6 6 isto ´, . e 5 x 5 6 3 6 · · = · y 6 5 4 5 5 6 Como · = 1, vem: 6 5 x 3 6 ·1 = · . y 4 5 x 3 5 x 3 6 Sendo = : e = · . y 4 6 y 4 5 3 5 3 6 ımos : = · . Conclu´ 4 6 4 5 O quociente de uma fra¸˜o por outra ´ igual ao produto da 1a fra¸˜o pelo ca e ca a inverso da 2 . 31 CEDERJ
- 34. Fra¸oes c˜ Exerc´ ıcios 1. Calcule: 5 10 3 9 1 4 a) : c) : e) 2 :3 3 3 5 7 7 14 3 1 19 38 b) 6 : d) : f) 5 3 80 40 5 4 2. Calcule o valor das seguintes express˜es: o 3 1 1 1 a) + : − 5 5 3 4 1 1 1 1 b) 1− · 1− 1− : 1− 2 3 4 6 11 1 1 3 c) : + : 5 4 3 4 1 1 7 1 1 5 1 1 d) − : + · 3 − · : 2 4 6 7 4 3 3 7 3. Jo˜o tem o sal´rio incluindo as horas extras de R$ 3.840,00. Jo˜o a a a 1 gasta metade do sal´rio para alimentar sua fam´ a ılia, gasta do sal´rio a 4 3 no aluguel da casa e do restante em condu¸˜o. ca 16 a) Quanto custa o aluguel da casa do Jo˜o? a b) Quanto a fam´ de Jo˜o gasta em condu¸˜o? ılia a ca c) Que fra¸˜o do sal´rio sobra para outras despesas? ca a Gabarito 1 7 1 15 12 1. a) b) 18 c) d) e) f) 2 15 4 23 25 48 3 396 37 2. a) b) c) d) 5 10 125 36 13 3. a) R$ 960,00 b) R$ 180,00 c) 64 CEDERJ 32
- 35. Fra¸oes c˜ ´ MODULO 1 - AULA 1 Sugest˜es e Solu¸˜es das Atividades Propostas o co Atividade 01 Explique de maneira convincente o porque dos n´ meros 1134 e 53172 u s˜o divis´ a ıveis por 9. Solu¸˜o: ca Vocˆ deve ter se lembrado do crit´rio de divisibilidade por 9, que ´ sim- e e e ples: um n´ mero ´ divis´ por 9 se, e somente se, a soma de seus algarismos u e ıvel for divis´ por 9. Assim, como 1 + 1 + 3 + 4 = 9, 1134 ´ divis´ por 9. ıvel e ıvel Mas, isso ´ convincente? Bem, se vocˆ simplesmente acredita nas regras, n˜o e e a h´ mais nada a discutir. No entanto, essa n˜o ´ uma atitude matem´tica a a e a muito positiva. Regras s˜o importantes pois s˜o muito uteis em situa¸˜es a a ´ co pr´ticas, fazem parte da cultura matem´tica. Mas, ´ fundamental entender a a e o porque da regra funcionar. Neste caso, a explica¸˜o ´ simples. Devido ao ca e nosso sistema num´rico decimal, 1134 = 1 × 1000 + 1 × 100 + 3 × 10 + 4. e Agora, como 1000 = 999 + 1, 100 = 99 + 1 e 10 = 9 + 1, podemos escrever 1134 = 1 × (999 + 1) + 1 × (99 + 1) + 3 × (9 + 1) + 4 = = [1 × 999 + 1 × 99 + 3 × 9] + [1 + 1 + 3 + 4]. Como o n´ mero [1 × 999 + 1 × 99 + 3 × 9] ´ divis´ por 9, claramente u e ıvel 1134 ´ divis´ por 9 se, e somente se, 1+1+3+4 ´ divis´ por 9. Repita e ıvel e ıvel o racioc´ ınio com o outro n´ mero. Observe que essa explica¸˜o ´ ilustrativa u ca e mas n˜o ´ uma demonstra¸˜o do crit´rio de divisibilidade por 9, uma vez que a e ca e usamos apenas um exemplo. Atividade 02 Por que ´ dif´ decompor o n´ mero 97343 em fatores primos? e ıcil u Solu¸˜o: ca Quanto tempo vocˆ gastou com esse exerc´ e ıcio? Bem, a id´ia aqui ´ e e colocar a teoria e a pr´tica em contato. A teoria ´ o maravilhoso Teorema a e Fundamental da Aritm´tica que afirma que todo natural admite uma unica e ´ decomposi¸˜o em fatores primos. A pr´tica ´ o ganha-p˜o de muitos ma- ca a e a tem´ticos: pode ser muito, muito dif´ decompor um n´ mero em fatores a ıcil u primos. Determinar se um dado n´ mero ´ primo ou n˜o j´ ´ uma tarefa u e a a e titˆnica. Procure saber sobre os chamados primos de Mersenne e vocˆ ter´ a e a uma id´ia melhor do que isso quer dizer. Mas, voltemos ` nossa vaca fria: e a por que ´ dif´ decompor o n´ mero 97343 em fatores primos? e ıcil u 33 CEDERJ
- 36. Fra¸oes c˜ A pergunta tem um certo subjetivismo e vocˆ poderia ter respondido: e mas n˜o ´ dif´ decompor este n´ mero, veja: 97343 = 311 × 313. a e ıcil u A eventual dificuldade reside no fato de que para decompor ter´ ıamos que tentar a sua divisibilidade por todos os primos menores do que 311. Moral da Hist´ria: se os fatores primos de um n´ mero forem relativa- o u mente grande, ´ dif´ obter sua decomposi¸˜o em fatores primos. e ıcil ca Atividade 03 Quais das seguintes equa¸˜es podem ser resolvidas no ˆmbito dos n´ meros co a u naturais? E no ˆmbito dos n´ meros inteiros? a u a) x + 2 = 7 c) 3x + 7 = 4 e) 2x + 5 = 7 b) x + 4 = 1 d) 2x + 4 = 8 f) 2x + 6 = 13 Solu¸˜o: ca As equa¸˜es (a), (d) e (e) tˆm respostas 5, 2 e 1, respectivamente. co e Portanto, podem ser resolvidas no conjunto dos n´ meros naturais. J´ as u a equa¸˜es (b) e (c) demandam um conjunto maior, uma vez que ´ preciso co e subtrair 3 de 4 e de 7 para obtermos 1 e 4, respectivamente. Assim, as res- postas de (b) e (c) s˜o, respectivamente, −3 e −1. Finalmente, para resolver a a equa¸˜o (f) precisamos de um n´ mero tal que, somado a si mesmo resulte ca u em 7, um n´ mero ´ u ımpar. Ora, n˜o h´, no conjunto dos inteiros, um n´ mero a a u com tal caracter´ ıstica. Para resolver essa equa¸˜o (muito simples), preci- ca samos estender os inteiros a um conjunto maior, o que chamamos conjunto dos racionais... O nome cient´ ıfico do bicho ´ corpo de fra¸˜es dos n´meros e co u inteiros. Mas, n˜o se preocupe. Chegar´ a hora de vocˆ aprender esse latim a a e ´ todo, quando vocˆ fizer as disciplinas de Algebra. e Atividade 04 Use a defini¸˜o anterior de igualdade de n´ meros racionais para verifi- ca u 3 −3 car que = . −5 5 Solu¸˜o: ca 3 −3 Para verificar a igualdade = , devemos verificar se 3 × 5 ´ igual e −5 5 a (−3) × (−5), que ´ verdade, pois ambos produtos s˜o iguais a 15. e a CEDERJ 34
- 37. Fra¸oes c˜ ´ MODULO 1 - AULA 1 Atividade 05 2 1 Determine o valor de x tal que = . x−1 3 Solu¸˜o: ca 2 Antes de qualquer coisa, para que seja um leg´ıtimo n´ mero ra- u x−1 cional, uma fra¸˜o, ´ necess´rio que x seja diferente de 1, pois x − 1 deve ser ca e a diferente de zero. Mas, considerando essa condi¸˜o, fazemos (x−1)×1 = 2×3, ca ou seja, x − 1 = 6, cuja solu¸˜o ´ x = 7, que respeita a condi¸˜o x = 1. ca e ca 35 CEDERJ
- 39. N´meros Decimais u ´ MODULO 1 - AULA 2 Aula 2 – N´ meros Decimais u Introdu¸˜o ca H´ um livro maravilhoso, escrito por Tobias Dantzig, cujo t´ a ıtulo ´ e “N´ mero, a Linguagem da Ciˆncia”. N˜o h´ afirma¸˜o mais verdadeira. u e a a ca Seria imposs´ atingir o desenvolvimento cient´ ıvel ıfico-tecnol´gico a que chega- o mos sem dispor de ferramenta t˜o eficaz quanto os sistema num´rico decimal a e representado por algarismos hindu-ar´bicos. a Esse sistema, que o mundo todo usa, tem suas origens na ´ India, por volta de 200 aC, foi adotado pelos ´rabes no s´culo 8. Em 711 os ´rabes a e a cruzaram o Estreito de Gibraltar e invadiram a Pen´ ınsula Ib´rica, levando e na bagagem os algarismos e tantos outros conhecimentos, de astronomia, medicina, e hoje enriquecem a cultura ocidental. O resto da Europa eventu- almente se rendeu ao novo sistema, mas n˜o o fez sem muita resistˆncia. a e A grande qualidade do sistema num´rico decimal, representado pelos e algarismos hindu-ar´bicos, os nossos n´ meros de cada dia, ´ sua simplicidade, a u e aliada a uma nota¸˜o extremamente feliz – posicional. Ao escrevermos 11 031, ca onze mil e trinta e um, usamos o algarismo 1 em trˆs situa¸˜es, com diferentes e co significados, diferenciados apenas por suas posi¸˜es em rela¸˜o aos demais co ca algarismos, o 3 e o 0. Essa conquista estupenda, tanto para a Matem´tica quanto para as a demais ciˆncias, se fez sem alarde nem nomes – de maneira anˆnima – bem e o ao estilo da cultura hindu. Isso s´ foi poss´ devido ` introdu¸˜o de um s´ o ıvel a ca ımbolo representando o nada – a coluna vazia. Isso n˜o fora considerado pelas outras culturas, a representar o vazio era inconceb´ ıvel. Veja que a etimologia da palavra zero ´ do latim zephyrum, o nome do vento oeste, que provem de sifr, ´rabe para e a vazio, pronunciado vulgarmente s´fer. Sem o zero n˜o poder´ e a ıamos diferenciar 11 031 de 1 131. Atividade 01 Vocˆ sabe escrever 11 031 usando n´ meros romanos? Experimente mul- e u tiplicar, por exemplo, MMMCDXXIII por CLVII . . . 37 CEDERJ
- 40. N´meros Decimais u N´ meros Decimais – os n´ meros nossos de cada dia u u Quando falamos em n´ meros, com as pessoas comuns, os n´ meros com u u os quais lidamos na nossa vida di´ria, na padaria, no ˆnibus, no posto de a o gasolina, estamos nos referindo a uma classe bem especial de n´ meros u racionais – os chamados n´ meros decimais. Veja alguns exemplos: u 1205 −11, 7547 9, 82 10 000, 00 0, 000349 171 Esses n´ meros podem representar medidas de comprimento, pre¸os de u c objetos, notas de provas, ´ ındices dos mais diversos e muito mais. Apesar de serem uma parcela realmente pequena de n´ meros, mesmo se considerarmos u apenas o conjunto dos n´ meros racionais, eles bastam para a maioria das u nossas necessidades di´rias. Veja a defini¸˜o de n´ meros decimais: a ca u Os n´meros decimais s˜o todos aqueles que podem ser escritos na u a p forma ± n , com p e n inteiros tais que p, n ≥ 0. 10 Assim, a lista anterior pode ser reconhecida como 1205 117547 982 1205 = −11, 7547 = − 9, 82 = 1 10 000 100 10000 349 171 10 000, 00 = 0, 000349 = 171 = 1 1000000 1 Fra¸˜o decimal ca Observe as fra¸˜es escritas abaixo: co 5 2 3 25 , , , 10 100 1000 10000 ↑ ↑ ↑ ↑ 101 102 103 104 Os denominadores s˜o potˆncias de 10. a e Defini¸˜o: Denomina-se fra¸˜o decimal toda fra¸˜o em que o denomina- ca ca ca dor ´ uma potˆncia de 10 com o expoente natural. e e CEDERJ 38
- 41. N´meros Decimais u ´ MODULO 1 - AULA 2 Numeral decimal Sabemos que cada algarismo que comp˜e um numeral ocupa certa or- o dem. Assim, no numeral: 4689 O valor dos algarismos deste numeral depende da ordem que ele ocupa. Como 4689 = 4 × 1000 + 6 × 100 + 2 × 10 + 9, ent˜o a O algarismo 4 na ordem das unidades de milhar −→ vale 4 · 1000 O algarismo 6 na ordem das centenas −→ vale 6 · 100 O algarismo 8 na ordem das dezenas −→ vale 8 · 10 O algarismo 9 na ordem das unidades −→ vale 9 · 1 Quando um algarismo ´ deslocado uma ordem ` direita, seu valor passa e a 1 a ser 10 do anterior. E, quando ele ´ deslocado ` esquerda o seu valor passa e a a ser 10× o anterior. Para representar os n´ meros racionais de outro modo, vamos apresentar u os n´ meros decimais. Como teremos que representar partes da unidade, u ampliaremos o sistema de numera¸˜o decimal. ca 1o ) Colocaremos uma v´ ırgula para separar as unidades inteiras das partes da unidade. 2o ) Criaremos novas ordens, chamadas ordens decimais ou casas decimais, ` a 1 direita da v´ ırgula, obedecendo ao princ´ ıpio de cada ordem vale do que 10 est´ a sua esquerda. a Eis alguns numerais e como devem ser lidos: 0,8 → oito d´cimos e 0,18 → dezoito cent´simos e 5,8 → cinco inteiros e oito d´cimos e 7,20 → sete inteiros e vinte cent´simos e 19,421 → dezenove inteiros e quatrocentos e vinte e um mil´simos e Fra¸˜o decimal e numeral decimal ca Transforma¸˜o de numeral decimal em fra¸˜o decimal. ca ca Transformar 0, 043 em fra¸˜o decimal. ca 43 0, 043 = 1000 39 CEDERJ
- 42. N´meros Decimais u Portanto, Para transformar um numeral decimal em fra¸˜o decimal escreve-se uma ca fra¸˜o cujo numerador ´ o numeral decimal sem a v´ ca e ırgula e cujo deno- minador ´ o algarismo 1 seguido de tantos zeros quantas forem as casas e decimais do numeral dado. Exemplos: 4723 1) 47, 23 = ↓ 100 → 2 zeros 2 casas decimais 431 2) 0, 00431 = ↓ 100000 → 5 zeros 5 casas decimais Transforma¸˜o de fra¸˜o decimal em numeral decimal. ca ca 35 Transformar em numeral decimal. 10000 35 35 representa 35 d´cimos de mil´simos, logo e e = 0, 0035 10000 10000 Para transformar uma fra¸˜o decimal em n´ mero decimal escreve-se o ca u numerador da fra¸˜o com tantas ordens decimais quantos forem os zeros ca do denominador. Exemplos: 324 34 1) = 32, 4 2) = 0, 0034 10 ↑ 10000 ↑ ↑ 1 casa ↑ 4 casas 1 zero decimal 4 zeros decimais Propriedades dos n´meros decimais. u Consideremos 4,31 431 Sabemos que 4, 31 = 100 Vamos multiplicar os termos dessa fra¸˜o por 10, por 100 e por 1000. ca 431 4310 43100 431000 = = = 100 1000 10000 100000 CEDERJ 40
- 43. N´meros Decimais u ´ MODULO 1 - AULA 2 Se transformarmos cada fra¸˜o em numeral decimal, obtemos: ca 4, 31 = 4, 310 = 4, 3100 = 4, 31000 Conclu´ ımos ent˜o a 1a Propriedade: Um numeral decimal n˜o se altera quando retiramos ou acrescentamos a um ou mais zeros ` direita da sua parte decimal. a Exemplos: 1) 34, 1 = 34, 10 = 34, 100 = 34, 1000 2) 4, 181 = 4, 1810 = 4, 18100 = 4, 181000 Conseq¨ˆncia ue A principal conseq¨ˆncia da 1a propriedade ´ que dois n´ meros decimais ue e u quaisquer podem sempre ser representados com o mesmo n´ mero de ordens u decimais. Exemplo: 4,156 e 2,14 podem ser escritos: 4,156 e 2,140 (ambos com 3 casas) Consideremos 4,518. Multipliquemos esse numeral por 10, por 100 e por 1000: 4518 10 / 4518 4, 518 × 10 = × = = 45, 18 1000 / 1 100 4518 4518 4, 518 × 100 = × 100 = // = 451, 8 // 1000 10 4518 4, 518 × 1000 = /// × 1000 = 4518 /// 1000 Da´ temos: ı 2a Propriedade: Para multiplicar um numeral decimal por 10, por 100, por 1000, etc, basta deslocar a v´ ırgula uma, duas, trˆs, etc, casas decimais para a direita. e 41 CEDERJ
- 44. N´meros Decimais u Exemplos: 1) 13, 4 × 10 = 134 2) 431, 45 × 100 = 43145 3) 0, 00412 × 1000 = 4, 12 Aplica¸˜o - Compara¸˜o de decimais ca ca A 2a propriedade ´ aplicada na compara¸˜o de numerais decimais. e ca Exemplo: Comparar os numerais 0, 345 e 0, 2431 1◦ ) Reescrevemos os dois decimais com igual n´ mero de casas (1a proprie- u dade) 0, 3450 e 0, 2431 2◦ ) Eliminamos a v´ ırgula (multiplicar por 10000) e comparamos os n´ meros u restantes. 3450 > 2431 ent˜o 0, 345 > 0, 2431. a Vamos dividir 314,21 por 10, por 100 e por 1000. 31421 31421 1 31421 314, 21 : 10 = : 10 = · = = 31, 421 100 100 10 1000 31421 31421 1 31421 314, 21 : 100 = : 100 = · = = 3, 1421 100 100 100 10000 31421 31421 1 31421 314, 21 : 1000 = : 1000 = · = = 0, 31421 100 100 1000 100000 Da´ temos: ı 3a Propriedade: Para dividir um n´ mero decimal por 10, por 100, por 1000, etc, basta u deslocar a v´ ırgula uma, duas, trˆs, etc, casas decimais para a esquerda. e Exemplos: 1) 5,21 : 10 = 0,521 2) 434,25 : 100 = 4,3425 3) 3,421 : 1000 = 0,003421 CEDERJ 42
- 45. N´meros Decimais u ´ MODULO 1 - AULA 2 Nota¸˜o Cient´ ca ıfica ´ E comum precisarmos comparar n´ meros decimais. Esse processo pode u ser facilitado se usarmos uma conven¸˜o a que chamamos nota¸˜o cient´ ca ca ıfica. A nota¸˜o cient´ ca ıfica de um n´ mero decimal ´ escrevˆ-lo na forma u e e n ± a × 10 onde a ´ um decimal tal que 1 ≤ a < 10, com n um inteiro. e O fator 10n ´ a ordem de grandeza do n´ mero. e u Veja, no quadro a seguir exemplos de n´ meros com suas respectivas u nota¸˜es cient´ co ıficas e ordens de grandeza. 147, 357 1, 47357 × 102 2 0, 0000567 5, 67 × 10−5 −5 −22052 −2, 2052 × 104 4 0, 005 × 10−4 5, 0 × 10−7 −7 Exerc´ ıcios 1. Transforme em fra¸˜es decimais. co a) 0,3 c) 11,43 e) 9,2324 b) 1,34 d) 0,222 f) 0,0014 2. Transforme um numeral decimal. 8 138 1723 a) c) e) 1000 100 100 54 41 324 b) d) f) 5 10 1000 10 3. Transforme as porcentagens abaixo em n´ mero decimal e em fra¸˜o u ca decimal. a) 18% c) 50% b) 34% d) 70% 4. Um professor recebia R$ 200,00 por aula e teve um aumento de 35%. Quanto passou a ganhar por aula? 5. Efetue a) 0, 34×10 c) 0, 004×1000 e) 0, 74 : 100 g) 0, 1 : 1000 b) 0, 0453 × 100 d) 42, 1 × 105 f) 4, 3 : 10 43 CEDERJ
- 46. N´meros Decimais u Gabarito 3 134 1143 222 92324 14 1. a) b) c) d) e) f) 10 100 100 1000 10000 10000 2. a) 0,008 b) 5,4 c) 1,38 d) 0,041 e) 17,23 f) 0,00324 18 34 50 7 3. a) 0,18 e b) 0,34 e c) 0,5 e d) 0,7 e 100 100 100 10 4. R$ 270,00 5. a) 3,4 b) 4,53 c) 4 d) 4210000 e) 0,0074 f) 0,43 g) 0,0001 Adi¸˜o e subtra¸˜o de decimais ca ca Adi¸˜o ca Para calcular a soma 3,6 + 0,38 + 31,424 podemos converter os decimais em fra¸˜es e som´-las: co a 36 38 31424 3600 + 380 + 31424 + 3, 6 + 0, 38 + 31, 424 = + = 10 100 1000 1000 35404 = = 35, 404 1000 Ou simplesmente somar os n´ meros decimais da seguinte forma: u 3, 600 0, 380 31, 424 + 35, 404 Portanto para somar numerais decimais: 1◦ ) Igualamos o n´ mero de casas decimais das parcelas, acrescentando zeros. u 2◦ ) Colocamos v´ ırgula debaixo de v´ ırgula. 3◦ ) Somamos como se fossem n´ meros naturais e colocamos a v´ u ırgula ali- nhada com as outras. Subtra¸˜o ca Para subtrair numerais decimais, procedemos de modo similar ao usado na adi¸˜o. ca Exemplo: 29,34 - 14,321 29, 340 14, 321 − 15, 019 CEDERJ 44
- 47. N´meros Decimais u ´ MODULO 1 - AULA 2 Multiplica¸˜o de decimais ca Para calcular o produto 3, 6 × 18, 36 podemos converter os decimais em fra¸˜es e multiplic´-las. co a 36 1836 66096 3, 6 × 18, 36 = × = = 66, 096 10 100 1000 Ou simplesmente multiplicar esses n´ meros da seguinte forma: u 3, 6 18, 36 216 108 288 36 66, 096 Da´ temos que para multiplicar numerais decimais: ı 1◦ ) Multiplicamos os decimais como fossem n´ meros naturais. u ◦ 2 ) Damos ao produto tantas casas decimais quanto seja a soma dos n´ meros de casas decimais dos fatores. u Divis˜o de decimais a Divis˜es exatas o Exemplo 1: Vamos achar o quociente de 10 por 4. No conjunto dos naturais ´ 2, mas vamos obter o resto 2. e 10 | 4 2 2 ⌣ Podemos neste caso obter um quociente mais preciso (com resto 0) se continuarmos a divis˜o. a O que faremos ent˜o? a Vamos acrescentar um zero ao resto (significa multiplicar o resto por 10), para n˜o alterar o resultado basta dividirmos o quociente por 10, isto a significa colocar uma v´ırgula no quociente depois do 2. Assim teremos: 10 | 4 10 | 4 10 | 4 20 2, 5 −→ −→ 2 2 20 2, 0 ⌣ 45 CEDERJ
- 48. N´meros Decimais u Exemplo 2: Vamos dividir 30 por 8. De modo similar ao exemplo 1, vem: 30 | 8 30 | 8 60 3, 75 30 | 8 30 | 8 −→ −→ 60 3, 7 −→ 6 3 60 3, 40 4 0 ⌣ Em resumo, h´ divis˜es entre naturais em que ap´s alguns passos conse- a o o guimos, obter um quociente decimal e resto 0. Nesses casos, o quociente ´ chamado de decimal exato. e Divis˜es n˜o exatas o a Nem sempre a divis˜o acaba por apresentar resto 0. a Exemplo: Vamos calcular 211 : 90 1◦ passo 211 | 90 Como h´ um resto, o quociente ser´ da forma 2, . . . a a 31 2 Notamos que o quociente ´ maior que 2 e menor que 3. e 2◦ passo 3◦ passo 4◦ passo 211 | 90 211 | 90 211 | 90 310 2, 34 310 2, 344 310 2, 3 −→ −→ 400 400 40 40 400 Observamos que, mesmo prosseguindo na divis˜o, jamais obteremos a resto zero. O algarismo 4 ir´ repetir-se como resto e obteremos aproxima- a dos, por falta, do quociente, assim 2,344; 2,3444; 2,34444; etc. Note que o algarismo 4 se repete. Logo temos: H´ divis˜es n˜o exatas em que conseguimos obter apenas valores apro- a o a ximados para o quociente, porque nunca se obt´m resto zero. Pelo e fato de haver algarismos que se repetem periodicamente no quociente, o quociente ´ chamado de d´ e ızima peri´dica. o CEDERJ 46
- 49. N´meros Decimais u ´ MODULO 1 - AULA 2 Transformar uma d´ ızima peri´dica em fra¸˜o o ca Exemplo 1: 0, 333 . . . Esta d´ ızima ´ chamada d´ e ızima peri´dica simples, pois depois da v´ o ırgula s´ tem a parte que repete. o Solu¸˜o ca 0, 333 . . . = (×10) 3, 333 . . . = 10 − 0, 333 . . . = 1 3 1 3 = 9 =⇒ = = 9 3 1 Logo, temos que 0, 333 . . . = . 3 Exemplo 2: 1, 424242 . . . ´ E uma d´ızima peri´dica simples. o 1, 424242 . . . = 142, 4242 . . . = 100 − 1, 4242 . . . = 1 141 42 141 = 99 =⇒ = =1 99 99 Obs.: 1) Se a parte que repete ´ 1 algarismo, devemos multiplicar por 10, se a e parte que se repete s˜o 2 algarismos devemos multiplicar por 100, etc . . . a na d´ ızima peri´dica simples. o 2) A fra¸˜o obtida ´ chamada geratriz da d´ ca e ızima. Exemplo 3: 2, 3444 . . . Esta d´ ızima ´ chamada d´ e ızima peri´dica composta, pois depois da o v´ ırgula tem parte que repete (4) e parte que n˜o repete (3). a Solu¸˜o ca 2, 3444 . . . = 234, 44 . . . = 100 (multiplicar at´ a parte que repete) e − 23, 44 . . . = 10 (multiplicar at´ a parte que n˜o repete) e a 211 31 211 = 90 =⇒ = =2 90 90 47 CEDERJ
- 50. N´meros Decimais u Divis˜o de decimais a Calcular o quociente 3, 24 : 1, 8 324 18 324 10 324 3, 24 : 1, 8 = : = · /= 100 10 100 18 180 / Logo, dividir 3, 24 por 1, 8 ´ o mesmo que dividir 324 por 180. e 324 | 180 1440 1, 8 0 ⌣ Da´ para dividir dois decimais: ı 1◦ ) Igualamos o n´ mero de casas decimais do dividendo e do divisor, acres- u centando zeros. 2◦ ) Eliminamos as v´ ırgulas. 3◦ ) Dividimos os n´ meros naturais que resultam das etapas anteriores. u Conjuntos num´ricos e Vimos a representa¸˜o dos conjuntos num´ricos: ca e N ´ o conjunto dos n´ meros naturais. e u N = {1, 2, 3, . . . }. Z ´ o conjunto dos n´ meros inteiros. e u Z = {. . . , −2, −1, 0, 1, 2, . . . } Q ´ o conjunto dos n´ meros racionais, que s˜o aqueles que podem ser e u a escritos em forma de fra¸˜o. ca a Q = x | x = , a, b ∈ Z, b = 0 . b Portanto, os n´ meros inteiros, os n´ meros decimais exatos e as d´ u u ızimas peri´dicas s˜o n´ meros racionais. o a u O conjunto dos n´ meros que n˜o podem ser representados por fra¸˜es u a co s˜o denominados n´ meros irracionais e representamos por I. Pode-se de- a u monstrar, em estudos mais avan¸ados, que os n´ meros irracionais s˜o exata- c u a mente as d´ ızimas n˜o peri´dicas. a o CEDERJ 48
- 51. N´meros Decimais u ´ MODULO 1 - AULA 2 Exemplo: √ 2 = 1, 414213 . . . e = 2, 7182818 . . . π = 3, 1415926 . . . O conjunto dos n´ meros racionais e irracionais ´ denominado n´ meros u e u reais e representamos por R. Nota: Na representa¸˜o de conjuntos num´ricos s˜o usadas as conven¸˜es: ca e a co (i) Sinal (+): elimina os n´ meros negativos de um conjunto. u Exemplo: Z+ = {0, 1, 2, 3, . . . } (conjunto dos n´ meros inteiros n˜o ne- u a gativos). (ii) Sinal (−): elimina os n´ meros positivos de um conjunto. u Exemplo: Z− = {. . . , −3, −2, −1, 0} (conjunto dos n´ meros inteiros n˜o u a positivos). (iii) Sinal (∗): elimina o n´ mero 0 (zero) de um conjunto. u Exemplo: Z∗ ´ o conjunto dos n´ meros inteiros n˜o nulos. e u a Exemplo: R∗ ´ o conjunto dos n´ meros reais n˜o nulos. e u a Exerc´ ıcios 1. Efetue as seguintes opera¸˜es: co a) 7,48 + 4,3 b) 0,4143 + 3,04 + 51,4 c) 78,05 + 5,8 d) 3,41 - 1,4 e) 43,1 - 11,4 f) 3,41 × 4 g) 11,4 × 10,5 h) 0,01 × 43,4 i) (1,3) × 1,4 + 0,001 × 100 j) 1,64 + 3,1 × 4,3 - 2,3 l) 27,34 + 81,43 - 7,45 49 CEDERJ
- 52. N´meros Decimais u m) 65 : 2 n) 1 : 20 o) 1870 : 20 p) 274 : 16 q) 8 : 3 r) 88,2 : 21 s) 40 : 11 2. Calcule os quocientes a) 2,4 : 0,12 c) 2,56 : 0,16 b) 0,02 : 4 d) 5,14 : 0,3 3. Calcule (0, 1) · (0, 001) · 0, 1 10 · 0, 0001 4. Determine a soma 0, 333 . . . + 0, 777 . . . 5. Calcule 0, 999 . . . 6. Determinar a fra¸˜o de cada d´ ca ızima peri´dica: o a) 0, 222 . . . b) 0, 232323 . . . c) 3, 1133 . . . Gabarito 1. a) 11, 78 b) 54, 8543 c) 83, 85 d) 2, 01 e) 31, 7 f) 13, 64 g) 119, 70 h) 0, 434 i) 1, 92 j) 12, 67 l) 101, 32 m) 32, 5 n) 0, 05 o) 93, 5 p) 17, 125 q) 2, 666 . . . r) 4, 2 s) 3, 636363 . . . 2. a) 20 b) 0, 005 c) 16 d) 17, 1333 . . . 3. 0, 01 10 4. 9 5. 1 2 23 17 6. a) b) c) 3 9 99 150 CEDERJ 50
- 53. N´meros Decimais u ´ MODULO 1 - AULA 2 Sugest˜o e Solu¸˜o da Atividade Proposta a ca Atividade 01 Escreva os n´ meros a seguir usando a nota¸˜o cient´ u ca ıfica. 22000000 0, 012 −0, 037 15 × 10−3 151 × 10−3 Solu¸˜o: ca 22000000 = 2, 2 × 107 ; 0, 012 = 0, 0001 = 1, 0 × 10−4; −0, 037 = −3, 7 × 10−2 ; 15 × 10−3 = 1, 5 × 10−4 ; 151 × 10−3 = 1, 51 × 10−1 . 51 CEDERJ
- 55. Potencia¸˜o ca ´ MODULO 1 - AULA 3 Aula 3 – Potencia¸˜o ca Vamos come¸ar esta aula com a defini¸˜o de potˆncias de n´meros reais. c ca e u O objetivo mais imediato da defini¸˜o ´ simplificar a nota¸˜o e fornecer um ca e ca m´todo para trabalhar com grandes n´ meros. No entanto, com o aprofun- e u damento do estudo, mais adiante no curso, vocˆ perceber´ que potencia¸˜o e a ca est´ na base das defini¸˜es das fun¸˜es logaritmo e exponencial. Esta ultima a co co ´ uma das mais importantes fun¸˜es da Matem´tica. co a Defini¸˜o 1 ca Seja a um n´ mero real e n um n´ mero natural, com n ≥ 2. u u A potˆncia de expoente n de a, denotada por an , ´ o n´ mero e e u an = a · a · a · ... · a n fatores Defini¸˜o 2 ca Seja a um n´ mero real n˜o nulo e n um n´ mero natural, u a u com n ≥ 2. A potˆncia de expoente −n de a, denotada por e −n a , ´ o n´ mero e u 1 1 1 1 a−n = · · · ... · a a a a n fatores Notas: 1. Se a ´ um n´ mero real qualquer escrevemos e u a1 = a . Tamb´m, no caso em que a = 0, assumimos por conven¸˜o que e ca a0 = 1 . a a a ´ 2. A express˜o 00 n˜o tem sentido matem´tico. E o que chamamos de uma indetermina¸˜o. Para entender um pouco mais o porque da im- ca possibilidade de dar sentido num´rico a 00 vocˆ deve aguardar o estudo e e das disciplinas de C´lculo. a 53 CEDERJ
- 56. Potencia¸˜o ca 3. Note que se a = 0 e n ´ um n´ mero natural vale e u n −n 1 a = . a 4. Finalmente, na express˜o an os n´ meros a e n s˜o chamados de base e a u a expoente, respectivamente. Exemplo 1 a) 43 = 4 × 4 × 4 = 64. b) (−3)4 = (−3) × (−3) × (−3) × (−3) = 81. c) (0, 2)3 = (0, 2) × (0, 2) × (0, 2) = 0, 008. 2 1 1 1 1 1 d) = × = 2 = . 3 3 3 3 9 e) 61 = 6. 4 −4 1 1 1 1 1 1 f) 3 = = × × × = . 3 3 3 3 3 81 −2 2 2 3 1 4 4 4 16 g) = 3 = = × = . 4 4 3 3 3 9 h) 102 = 10 × 10 = 100. i) 104 = 10 × 10 × 10 × 10 = 10000. 2 −2 1 1 1 1 j) 10 = = × = = 0, 01. 10 10 10 100 6 −6 1 1 1 1 1 1 1 k) 10 = = × × × × × = 0, 000001. 10 10 10 10 10 10 10 l) (−1)24 = 1. 3 −3 1 1 1 1 1 1 m) (−2) = = × × = =− . −2 −2 −2 −2 −8 8 CEDERJ 54
- 57. Potencia¸˜o ca ´ MODULO 1 - AULA 3 Propriedades das potˆncias e Sejam a e b n´ meros reais e m, n n´ meros inteiros. Supondo que as u u potˆncias expressas est˜o bem definidas ent˜o valem as seguintes proprieda- e a a des: Potˆncias de mesma base e Para multiplicar, mant´m-se a base e somam-se os expoentes, isto ´: e e am · an = am+n . Para dividir, mant´m-se a base e subtraem-se os expoentes, isto ´: e e am = am−n , a = 0 . an Potˆncias de mesmo expoente e Para multiplicar, mant´m-se o expoente e multiplicam-se as bases, isto ´: e e an · bn = (ab)n . Para dividir, mant´m-se o expoente e dividem-se as bases, isto ´: e e n an a = , b = 0. bn b Potˆncia de potˆncia e e Para calcular a potˆncia de outra potˆncia, mant´m-se a base e multiplicam- e e e se os expoentes, isto ´: e n am = am·n . Obs.: • Nas propriedades enunciadas a base deve ser n˜o-nula nas seguintes a situa¸˜es: o expoente ´ negativo ou a potˆncia est´ no denominador. co e e a • As propriedades tˆm a finalidade de facilitar o c´lculo. N˜o ´ obri- e a a e gat´rio o seu uso. Devemos us´-las quando for conveniente. o a • As propriedades enunciadas podem ser provadas a partir das defini¸˜es. co Por objetividade, partimos direto para os exemplos. 55 CEDERJ
- 58. Potencia¸˜o ca Exemplo 2 a) 32 × 33 = 32+3 = 35 = 243. 45 b) = 45−2 = 43 = 64. 42 c) 32 × 52 = (3 × 5)2 = 152 = 225. 4 64 6 d) 4 = = 24 = 16. 3 3 2 e) 33 = 33×2 = 36 = 729. 2 2 2 f) a2 b2 = a2 b2 = 44 b4 . Aplica¸˜o ca Todo n´ mero real positivo b pode ser expresso na forma b = a × 10p , u onde p ´ um n´ mero inteiro e a um n´ mero real, com 1 < a < 10. Esta e u u maneira especial de escrever o n´ mero b ´ denominado nota¸˜o cient´ u e ca ıfica. Exemplo 3 A nota¸˜o cient´ ca ıfica de 450 ´ 4, 5 × 102 e, a nota¸˜o cient´ e ca ıfica de 0, 042 ´ 4, 2 × 10−2 . e Exemplo 4 e ca ıfica do n´ mero 414 × 521 ? Qual ´ a nota¸˜o cient´ u Solu¸˜o: ca 14 414 ×521 = 22 ×521 = 228 ×521 = 27 ×221 ×521 = 128×1021 = 1, 28×1023 . Exerc´ ıcios Propostos 1. Efetue as opera¸˜es indicadas : co a) 23 × 26 f) (0, 3)2 × (0, 5)2 b) 32 × 36 × 3−4 g) (−0, 04)2 × (50)2 (−0, 6)2 c) 54 ÷ 52 h) (0, 2)2 398 d) i) 24 )3 395 3−4 3 e) −3 j) 24 3 CEDERJ 56
- 59. Potencia¸˜o ca ´ MODULO 1 - AULA 3 2 2. Determine o valor da express˜o 22 × 2−3 × 3−1 × 33 . a 3. Sendo a e b n´ meros reais diferentes de zero, determine o valor de u 3 2 3 ab 2. a2 b3 5−1 + 7−1 4. Determine o valor de . 3−1 5. Determine o valor da express˜o a 4 3 6 1 1 1 − ÷ − × − + 2−6 . 2 2 2 6. Determine o valor de (0, 2)3 + (0, 32)2. 7. Se a = 24 , b = a3 , c = 2a , determine o valor de 2abc2 . 102 × 10−4 × 10−3 8. Determine o valor de . 10−2 × 10−6 9. Encontrar o valor aproximado de 1.000.000 × (1, 09)160 adotando (1, 09)8 ∼ 2 e 210 = 1000. = ∼ 10. Determine a quantidade de algarismos do n´ mero 168 × 1259 . u 11. Qual ´ a metade de 222 ? e 2n + 2n+1 + 2n+2 12. Simplifique a fra¸˜o ca , onde n ∈ N. 2n+1 13. Determine a rela¸˜o entre a e b onde a e b s˜o n´ meros naturais que ca a u expressam os n´ meros de algarismos de x = 412 × 520 e y = 414 × 518 , u respectivamente. Gabarito 1. a) 29 b) 34 c) 52 d) 33 e) 3−1 f) 0, 0225 g) 4 h) 9 i) 212 j) 264 2. 81/4 8. 1000 5 3. a 9. um trilh˜o a 4. 36/35 10. 29 5. 1/128 11. 221 6. 0, 1104 12. 7/2 49 7. 2 13. a = b 57 CEDERJ
- 61. Radicia¸˜o ca ´ MODULO 1 - AULA 4 Aula 4 – Radicia¸˜o ca Nesta aula estudaremos radicia¸˜o que ´, conforme vocˆ perceber´, ca e e a a opera¸˜o inversa da potencia¸˜o. Vamos ` defini¸˜o. ca ca a ca Defini¸˜o 1 ca Seja a um n´ mero real e n um n´ mero natural. O n´ mero x u u u n ´ chamado raiz en´sima de a se, e somente se, x = a. Ou e e seja, temos a seguinte equivalˆncia: e x ´ raiz en´sima de a ⇐⇒ xn = a. e e Nota¸˜o ca √ Usaremos a nota¸˜o n a , para representar ra´ en´simas do n´ mero a. ca ızes e u √ No caso em que n = 2 e a > 0, em vez de a , escrevemos simplesmente 2 √ √ a e lemos “raiz quadrada de a”. Nesta situa¸˜o, − a ´ o sim´trico da ca e e √ 2 raiz quadrada de a e (− a) = a. Mais adiante vamos definir melhor a √ representa¸˜o n a. ca Existˆncia e Da defini¸˜o conclui-se que determinar as ra´ ca ızes en´simas de a ´ o e e mesmo que determinar todas as solu¸˜es da equa¸˜o xn = a. Vamos examinar co ca os seguintes casos: Primeiro caso: a = 0 e n ∈ N, n ≥ 2 A unica raiz en´sima de zero ´ o pr´prio zero, ou seja: ´ e e o √ n 0 = 0. Segundo caso: a > 0 e n ∈ N sendo n par O n´ mero a possui duas ra´ en´simas. Essas duas ra´ s˜o sim´tricas. u ızes e ızes a e √ A raiz en´sima positiva de a ´ representada pelo s´ e e ımbolo a. A raiz en´sima n e √ e e ımbolo − n a. negativa de a, por sim´trica da primeira, ´ representada pelo s´ 59 CEDERJ
- 62. Radicia¸˜o ca √ 4 √ 6 √ Portanto cuidado quando escrevemos, por exemplo, 3, 5, 3, estamos representando n´ meros positivos. u Exemplo 1 O n´ mero 16 tem duas ra´ u ızes quartas. A raiz quarta positiva de 16 ´ 2. e A raiz quarta negativa de 16 ´ -2. Assim, e √ 4 16 = 2 √ 4 − 16 = −2 . As ra´ quartas de 16 s˜o 2 e -2. ızes a Terceiro caso: a < 0 e n ∈ N sendo n par Neste caso n˜o existe raiz. O que queremos dizer com isto? Simples- a mente que no conjunto dos n´ meros reais n˜o tem sentido uma express˜o u a a √ √ como −2 ou −6 . 8 Exemplo 2 N˜o existe raiz quadrada de -4. Ou dito de outro modo, n˜o existe nenhum a a 2 n´ mero real x tal que x = −4. u Quarto caso: a = 0 e n ∈ N sendo n ´ ımpar O n´ mero a possui exatamente uma unica raiz en´sima no conjunto u ´ e dos n´ meros reais. Esta raiz tem o mesmo sinal de a e ´ representado pelo u e √ s´ ımbolo n a. Exemplo 3 a) O n´ mero 8 tem uma unica raiz c´ bica que ´ representada com o u ´ u e √3 ımbolo 8 e vale 2, isto ´, s´ e √ 3 8 = 2. b) O n´ mero −64 tem uma unica raiz c´ bica no conjunto dos n´ meros u ´ u u √ e ımbolo −64 e vale −4, isto ´: reais, que ´ representada pelo s´ 3 e √ 3 −64 = −4 . CEDERJ 60
- 63. Radicia¸˜o ca ´ MODULO 1 - AULA 4 Obs.: √ 1) No s´ ımbolo n a dizemos que: √ ´ o radical e a ´ o radicando e n ´ o´ e ındice da raiz. 2) Conforme j´ observado, por conven¸˜o, na raiz quadrada, omite-se o a ca √ √ √ ındice. Escreve-se, por exemplo, 6 e − 6 para representar 2 6 . ´ Exemplo 4 a) O n´ mero 8 ´ uma raiz quadrada de 64, pois 82 = 64. u e b) O n´ mero -8 ´ uma raiz quadrada de 64, pois (−8)2 = 64. u e √ c) 3 0 = 0. √ d) 16 = 4. √ e) − 16 = −4. √ f) ± 16 = ±4. √ g) −4 n˜o tem sentido em R. a √3 h) 27 = 3. √ i) 3 −27 = −3. √ j) 3 −1 = −1. √ k) 4 2401 = 7. Propriedades das Ra´ ızes Sejam a e b n´ meros reais e m, n n´ meros inteiros. Suponha que as u u ra´ ızes en´simas que escreveremos nas propriedades de 1 at´ 4, a seguir, s˜o e e a bem definidas. Ent˜o valem as seguintes propriedades: a Propriedade 1 (Radicais de mesmo ´ Indice) Para multiplicar, mant´m-se o ´ e ındice e multiplicam-se os radicandos, isto ´, e √ √ n √ n n a× b= ab . Para dividir, mant´m-se o ´ e ındice e dividem-se os radicandos, isto ´, e √ n a a √ = n , b = 0. n b b 61 CEDERJ
- 64. Radicia¸˜o ca Exemplo 5 √ √ √ a) 3 3 × 3 9 = 3 27 = 3 √ √ √ b) 2 × 5 = 10 √ √ √ c) 3 32 = 3 8 × 3 4 √ √ √ √ √ d) 8 = 2 × 4 = 2 × 2 = 2 2 Propriedade 2 (Raiz de Raiz) Para calcular uma raiz de outra raiz, mant´m-se o radicando e multiplicam- e se os ´ ındices, isto ´, e n √ √ m a = mn a . Exemplo 6 √3 √ a) 729 = 6 729 = 3 3 4 √ √ b) 5 = 24 5 Propriedade 3 (Raiz de Potˆncia) e Calcular a raiz e em seguida a potˆncia ´ o mesmo que calcular a potˆncia e e e e em seguida a raiz, isto ´, e √ m √ n n a = am , m ∈ Z . Exemplo 7 √ √ 5 a) 45 = 4 = 25 = 32 √ √ 2 b) 162 = 4 16 = 22 = 4 4 Propriedade 4 (Altera¸˜o do ´ ca Indice) Multiplicar ou dividir ´ ındice e expoente por um mesmo n´ mero n˜o altera u a o resultado, isto ´, e √ n √ am = np amp . Exemplo 8 √ 6 √ 6:3 √ a) 23 = 23:3 = 2 √ 16 √ 16:8 √ b) 28 = 28:8 = 2 √ √ √ 2×3 √ 3×2 √ c) 5 × 3 2 = 53 × 22 = 6 500 CEDERJ 62
- 65. Radicia¸˜o ca ´ MODULO 1 - AULA 4 Notas: 1. Voltamos a enfatizar que as propriedades enunciadas s˜o v´lidas sob a a a condi¸˜o que as potˆncias e radicais estejam bem definidas. Por exem- ca e plo, n˜o tem sentido usar a Propriedade 3 para escrever 4 (−2)3 = a √ 3 √ = 4 −2 , uma vez que n˜o tem sentido 4 −2 , no conjunto dos a n´ meros reais. u 2. As demonstra¸˜es das propriedades enunciadas n˜o s˜o dif´ co a a ıceis de serem realizadas. Basta um uso cuidadoso das defini¸˜es. Se vocˆ tiver tempo co e tente provar algumas delas. Se tiver dificuldade procure seu tutor, ou discuta com seus colegas de grupo de estudo. Nosso pr´ximo assunto tem como objetivo ampliar a utiliza¸˜o de potˆn- o ca e cias e radicais com o objetivo de facilitar opera¸˜es com n´ meros reais. Ou de co u um outro ponto de vista, veja a Defini¸˜o 2 a seguir, trataremos a radicia¸˜o ca ca como um caso especial de potˆncias de expoentes fracion´rios. e a Potˆncia de Expoente Racional e Defini¸˜o 2 ca a) Seja a un n´ mero real positivo, n um n´ mero natural n˜o-nulo e m um u u a n n´ mero racional na forma irredut´ u ıvel. A potˆncia de base a e expoente e racional m ´ definido por n e √ am/n = n am . b) Seja a um n´ mero real, n um n´ mero natural ´ u u ımpar e m um n´ mero n u racional na forma irredut´ ıvel. A potˆncia de base a e expoente racional e m n ´ definida por e m √ a n = n am . Nota: Valem para as potˆncias de expoente racional, as mesmas propriedades e v´lidas para as potˆncias de expoente inteiro. a e 63 CEDERJ
- 66. Radicia¸˜o ca Exemplo 9 √ a) 33/5 = 5 33 √ √ b) 21/7 = 7 7 21 = 2 √ c) 2−2/5 5 = 2−2 1 1 1+1 5 √ 6 d) 2 2 × 2 3 = 2 2 3 = 26 = 25 Racionaliza¸˜o ca Racionalizar o denominador de uma fra¸˜o significa eliminar os radicais do ca denominador sem alter´-la. a Exemplo 10 √ √ 1 1 √3 3 a) √ 3 = √ 3 × 3 = 3 2 2 √ 5 4 √ √2 5 b) √ 5 2 = √ 5 2 × 5 4 2 = 16 √ √ 3+ 2 √ √ 3+ 2 √ √ c) √ 1√ = √ 1 √ × √ √ = = 3+ 2 3− 2 3− 2 3+ 2 1 Exerc´ ıcios Propostos 1. Efetue: √ √ √ 3 a) 3 16 × 3 4 d) 272 √ 30 √ 8 b) √ e) 36 6 √ √ c) 256 f) 72 √ √ 2. Escrever 45 + 80 na forma de um unico radical. ´ 3 228 + 230 3. Efetue 10 4. Escreva na forma de um unico radical: ´ √ √ √ √ 3 2 4 3 a) 2 × 3 × 5 6 c) √5 3 √ 2 b) 3 2 d) 3 √ 4 3 √ √ 5. Dados os dois n´ meros 3 3 e 4 4, determine o maior. u CEDERJ 64
- 67. Radicia¸˜o ca ´ MODULO 1 - AULA 4 6. Escrever cada potˆncia na forma de radical: e a) 33/4 b) 31/7 c) 51/2 d) 2−2/3 1/2 7. Determine o valor de 93/2 − 272/3 . 8. Racionalizar o denominador: √ 3 5 1 1 a) √ b) √ c) √ 5 d) √ √ 2 7 27 5− 3 75 9. Simplificar . 12 √ √ 3+1 3−1 10. Simplifique √ +√ . 3−1 3+1 Gabarito √ √ 4 √ 1. a) 4 b) 5 c) 4 d) 9 e) 27 f) 6 2 √ 2. 7 5 3. 29 √ √ 32 16 4. a) 12 16200 b) 4 18 c) 15 27 d) 12 3 √ 5. 3 3 √ √ √ 1 6. a) 4 27 b) 7 3 c) 5 d) √ 3 √ 4 7. 3 2 √ √ √ 5 √ √ 8. a) 3 2 2 b) 735 c) 3 9 d) 5+ 3 2 9. 5/2 10. 2 Exerc´ ıcios de Refor¸o c √ 1, 777 . . . 1. (PUC-99) O valor de √ ´: e 0, 111 . . . 4 a) 4, 444 . . . b) 4 c) 4, 777 . . . d) 3 e) 3 2. (PUC-93) Somando as d´ ızimas peri´dicas 0, 4545 . . . e 0, 5454 . . . obt´m- o e se: a) um inteiro b) um racional maior que 1 c) um racional menor que 1 d) um irracional maior que 1 e) um irracional menor que 1 65 CEDERJ
- 68. Radicia¸˜o ca 3. (FGV-SP) Assinale a alternativa incorreta: a) Todo n´ mero inteiro ´ racional. u e b) O quadrado de um irracional ´ real. e c) A soma de dois n´ meros irracionais pode ser racional. u d) O produto de dois n´ meros irraiconais ´ sempre irracional. u e 4. Escrever na forma decimal os n´ meros: u 1 9 2 a= b= c= 2 5 45 5. Escreva na forma fracion´ria os n´ meros a u a = 0, 075 b = 2, 4141 . . . c = 1, 325151 . . . √ √ 6. (UF-AL-80) A express˜o 10 + 10 · 10 − 10 ´ igual a: a e √ √ √ a) 0 b) 10 c) 10 − 10 d) 3 10 e) 90 7. (CESGRANRIO-84) Dentre os n´ meros x indicados nas op¸˜es abaixo, u co 14 9 aquele que satisfaz < x < ´: e 11 7 a) 1,24 b) 1,28 c) 1,30 d) 1,32 e) 1,35 8. (UFF-1a fase) Se X e Y s˜o racionais onde X = 0, 1010101010 . . . e ¯ a Y = 0, 0101010101 . . . assinale a alternativa que representa o quociente de X por Y a) 0, 0101010101 . . . b) 0,11 c) 10, 10101010 . . . d) 10 9. (UFF 95 - 1a fase) Assinale qual das express˜es abaixo n˜o ´ um n´ mero ¯ o a e u real: 1 1 1 −2 −2 −3 1 √ 1 √ 1 a) − b) 3 π c) d) 3 −π e) − 2 2 3 10. (FUVEST) Usando (1, 41)2 < 2 < (1, 42)2, prove que 50 6, 1 < √ < 6, 3. 1 + 50 √ √ 11. (FUVEST) Seja r = 2 + 3. √ a) Escreva 6 em fun¸˜o de r. ca √ b) Admitindo que 6 seja irracional, prove que r tamb´m ´ irracio- e e nal. CEDERJ 66
- 69. Radicia¸˜o ca ´ MODULO 1 - AULA 4 12. (FUVEST) Sejam a, b e p n´ meros reais, a > 0, u b > 0 e p > 1. 2 a + bp a Demonstre: Se > p, ent˜o < p. a a+b b 13. (FATEC-SP) Se a = 0, 666 . . . , b = 1, 333 . . . e c = 0, 1414 . . . , calcule, ent˜o, a · b−1 + c. a 14. (PUC-RJ-80) Efetuadas as opera¸˜es indicadas, conclu´ co ımos que o n´ mero: u 1 2 2 × (3 − 7 ) +3 2/4 − 1/6 19 a) ´ > 5 b) est´ entre 2 e 3 c) ´ < e a e d) est´ entre 5 e 6 e) ´ > 6 a e 14 1 √ 15. (FATEC-SP-80) Sejam x ∈ R∗ , m = x − e y = 1 + m2 , ent˜o: a 4x 1 4x2 + 1 a) y = c) y = 2x √ √ 4x 4x4 + 4x2 + 2 x+1 b) y = d) y = 2x 2x Gabarito - Exerc´ ıcios de refor¸o c 1. b) 2. a) 3. d) 4. a = 0, 5, b = 1, 8, c = 0, 044 . . . 3 239 13219 5. a = ,b= ,c= 40 99 9900 6. d) 7. b) 8. d) 9. a) 10. Demonstra¸˜o ca √ r2 − 5 11. a) 6= b) Demonstra¸˜o ca 2 12. Demonstra¸˜o ca 127 13. 198 14. e) 15. d) 67 CEDERJ
- 71. Fatora¸˜o ca ´ MODULO 1 - AULA 5 Aula 5 – Fatora¸˜o ca Fatorar ´ transformar uma soma ou diferen¸a de duas ou mais parcelas e c como produto de dois ou mais fatores. Por exemplo, a express˜o cx + cy ´ a e equivalente ` express˜o fatorada c(x + y). Note que, cx + cy = c(x + y). a a A seguir vamos trabalhar algumas t´cnicas b´sicas de fatora¸˜o, entre e a ca as quais, fator comum, agrupamento, diferen¸as de quadrados, quadrado c perfeito, soma e diferen¸a de cubos e cubo perfeito. c Primeiro caso: Fator Comum a) ac + ad = a(c + d), a ´ fator comum de ac e ad e b) 2x2 − 3xy = x(2x − 3y), x ´ fator comum de 2x2 e 3xy e c) 36x2 y 2 − 48x3 y 4 = 12x2 y 2 3 − 4xy 2 , 12x2 y 2 ´ fator comum de 36x2 y 2 e e 48x3 y 4 . d) 3x2 + 6x3 + 12x4 = 3x2 1 + 2x + 4x2 , 3x2 ´ fator comum dos trˆs e e termos. Segundo caso: Agrupamento a) ac + bc + ad + bd = c(a + b) + d(a + b) = (a + b)(c + d) b) ab + ac − b − c = a(b + c) − 1(b + c) = (b + c)(a − 1) c) 6x2 − 4ax − 9bx + 6ab = 2x(3x − 2a) − 3b(3x − 2a) = (3x − 2a)(2x − 3b) d) ab + a − b − 1 = a(b + 1) − 1(b + 1) = (b + 1)(a − 1) Terceiro caso: Diferen¸a de Quadrados c A diferen¸a entre dois quadrados a2 − b2 ´ igual ao produto da soma c e a + b pela diferen¸a a − b. Assim, c a2 − b2 = (a + b)(a − b) . A justificativa ´ que: e (a + b)(a − b) = a(a − b) + b(a − b) = a2 − ab + ba − b2 = a2 − b2 . 69 CEDERJ
- 72. Fatora¸˜o ca Veja alguns exemplos: Exemplo 1 a) a2 − 16 = a2 − 42 = (a + 4)(a − 4) 2 b) 81 − m6 = 92 − m3 = 9 + m3 9 − m3 c) 4 − (x − y)2 = (2 + x − y)(2 − (x − y)) = (2 + x − y)(2 − x + y) Quarto caso: Quadrado Perfeito O desenvolvimento da express˜o (a + b)2 , resulta no quadrado da pri- a 2 meira parcela, a , somado com o dobro do produto das duas parcelas, 2ab, somado com o quadrado da segunda parcela, b2 , portanto, (a + b)2 = a2 + 2ab + b2 . A justificativa ´ que: e (a+b)2 = (a+b)(a+b) = a(a+b)+b(a+b) = a2 +ab+ba+b2 = a2 +ab+ab+b2 = a2 +2ab+b2 . O quadrado da diferen¸a entre duas parcelas (a − b)2 ´ igual ao quadrado da c e 2 primeira parcela, a , menos o dobro das duas parcelas, 2ab, mais o quadrado da segunda parcela b2 , isto ´, e (a − b)2 = a2 − 2ab + b2 . A justificativa ´ que: e (a−b)2 = (a−b)(a−b) = a(a−b)−b(a−b) = a2 −ab−ba+b2 = a2 −ab−ab+b2 = a2 −2ab+b2 . Obs.: N˜o confunda o quadrado da diferen¸a (a − b)2 com a diferen¸a de a c c quadrados a2 − b2 . (5 − 2)2 = 32 = 9 52 − 22 = 25 − 4 = 21 . Veja os exemplos a seguir: Exemplo 2 a) (2 − x)2 = 22 − 2 · 2x + x2 = 4 − 4x + x2 b) (3a − 2b)2 = (3a)2 − 2 · 3a · 2b + (2b)2 = 9a2 − 12ab + 4b2 CEDERJ 70
- 73. Fatora¸˜o ca ´ MODULO 1 - AULA 5 c) m2 − 6m + 9 = (m − 3)2 ↓ ↓ √ √ m 2 9 d) 25x2 + 30xy + 9y 2 = (5x + 3y)2 ↓ ↓ √ 25x2 9y 2 e) x2 + 4xy + 4y 2 = (x + 2y)2 ↓ ↓ √ x2 4y 2 Veja agora a t´cnica com um exemplo mais elaborado envolvendo fa- e tora¸˜o. Vamos simplificar as express˜es supondo cada denominador dife- ca o rente de zero: 10x2 − 10 10(x2 − 1) 10(x + 1)(x − 1) 10(x + 1) f) 2 − 2x + 1 = 2 = = x (x − 1) (x − 1)(x − 1) x−1 a2 − 4 (a + 2)(a − 2) (a + 2)(a − 2) a−2 g) 2 + 4a + 4 = 2 = = a (a + 2) (a + 2)(a + 2) a+2 Soma e Diferen¸a de Cubos c A soma de dois cubos ´ igual ao produto do fator a + b pelo fator e 2 2 a − ab + b , isto ´, e a3 + b3 = (a + b) a2 − ab + b2 . Diferen¸a de Cubos c A diferen¸a entre dois cubos ´ igual ao produto do fator a − b pelo fator c e 2 2 a + ab + b , isto ´, e a3 − b3 = (a − b) a2 + ab + b2 . 71 CEDERJ
- 74. Fatora¸˜o ca Justificativa (a + b) a2 − ab + b2 = = a a2 − ab + b2 + b a2 − ab + b2 = = a3 − a2 b + ab2 + ba2 − ab2 + b3 = = a3 − a2 b + ab2 + a2 b − ab2 + b3 = = a3 + b3 . (a − b) a2 + ab + b2 = = a a2 + ab + b2 − b a2 + ab + b2 = = a3 + a2 b + ab2 − ba2 − ab2 − b3 = = a3 + a2 b + ab2 − a2 b − ab2 − b3 = = a3 − b3 . Examine esses exemplos envolvendo fatora¸˜o: ca Exemplo 3 a) x3 + 8 = (x + 2) x2 − 2x + 4 b) 125 − 64m3 = (5 − 4m) 25 + 20m + 16m2 Veja novos exemplos envolvendo simplifica¸˜o de fra¸˜es com denomi- ca co nador diferente de zero: x3 − 8 (x − 2) x2 + 2x + 4 x2 + 2x + 4 c) = = x2 − 4 (x − 2)(x + 2) x+2 x3 + 64 (x + 4) x2 − 4x + 16 x2 − 4x + 16 d) = = x2 + 8x + 16 (x + 4)2 x+4 Cubo Perfeito O cubo da soma de duas parcelas ´ igual ao cubo da primeira parcela, e a , mais trˆs vezes o quadrado da primeira pela segunda, 3a2 b, mais trˆs 3 e e 2 vezes a primeira pelo quadrado do segundo, 3ab , mais o cubo da segunda parcela, b3 , portanto, (a + b)3 = a3 + 3a2 b + 3ab2 + b3 . O cubo da diferen¸a entre duas parcelas, (a − b)3 , ´ igual ao cubo da c e primeira parcela, a3 , menos trˆs vezes o quadrado da primeira pela segunda, e 3a b, mais trˆs vezes a primeira pelo quadrado do segundo, 3ab2 , menos o 2 e cubo da seginda parcela, b3 , portanto, (a − b)3 = a3 − 3a2 b + 3ab2 − b3 . CEDERJ 72
- 75. Fatora¸˜o ca ´ MODULO 1 - AULA 5 Justificativa (a + b)3 = (a + b)(a + b)2 = = (a + b) a2 + 2ab + b2 = = a a2 + 2ab + b2 + b a2 + 2ab + b2 = = a3 + 2a2 b + ab2 + a2 b + 2ab2 + b3 = = a3 + 3a2 b + 3ab2 + b3 . (a − b)3 = (a − b)(a − b)2 = = (a − b) a2 − 2ab + b2 = = a a2 − 2ab + b2 − b a2 − 2ab + b2 = = a3 − 2a2 b + ab2 − a2 b + 2ab2 − b3 = = a3 − 3a2 b + 3ab2 − b3 . Os exemplos a seguir utilizam as igualdades envolvendo cubos perfeitos e fatora¸˜o. Siga atentamente os c´lculos. ca a Exemplo 4 a) (3x+4y)3 = (3x)3 +3(3x)2 (4y)+3(3x)(4y)2 +(4y)3 = 27x3 +108x2y +144xy 2 +64y 3 b) (x − 2y)3 = x3 − 3x2 (2y) + 3x(2y)2 − (2y)3 = x3 − 6x2 y + 12xy 2 − 8y 3 c) a) 27 + 135x + 225x2 + 125x3 = (3 + 5x)3 ↓ ↓ √ 3 √ 3 27 = 3 125x3 = 5x d) b) 64 − 48x + 12x2 − x3 = (4 − x)3 ↓ ↓ √ 3 √ 3 64 = 4 x3 = x Exerc´ ıcios Propostos 1. Fatore: a) xy + 3y + x + 3 f) (2x + y)2 − (x − 2y)2 b) x2 − y 2 g) x8 − 1 c) 25x2 − 4y 2 h) 10a2 b3 c4 − 15a3 b2 c4 − 34a4 b3 c2 d) 36m2 − 100n2 i) mn − m − n + 1 e) 121 − 169a2 b2 j) y 4 − 16 73 CEDERJ
- 76. Fatora¸˜o ca 2. Simplifique: ab + a + b + 1 a) a2 − 1 a2 − b2 b) a2 + ab − a − b 3. Fatorar as seguintes express˜es: o a) 4x2 + 6xy + 2x f) 2x3 y 3 − 16x2 y 4 + 32xy 5 b) (a − b)2 + 2(a − b) g) 25 − x2 + 6xy − 9y 2 c) 2ab − ac − 2xb + xc h) x6 + y 6 d) 42x3 y − 70x2 y − 6x + 10 i) 8a3 − 1 e) 16x2 − 36 j) a3 − 3a2 b + 3ab2 − b3 4. Simplificar as fra¸˜es, supondo cada denominador diferente de zero: co dx − ex x4 − 1 a) f) mx − nx x4 − 2x2 + 1 ax4 − x3 a3 − 27 b) g) x3 y a2 + 3a + 9 x2 + xy + x + y a3 − 3a2 b + 3ab2 − b3 c) h) x2 − 1 a3 − b3 a3 + a2 − ab2 − b2 a2 − b2 d) i) a2 + ab + a + b a2 − 2ab + b2 (a − b)2 + 4ab e) 5a + 5b 1 1 5. Calcular o valor de a2 + 2 se a + = 6. a a 6. Os n´ meros naturais a e b, com a > b, s˜o tais que a2 − b2 = 7. u a Determine o valor de a − b. CEDERJ 74
- 77. Fatora¸˜o ca ´ MODULO 1 - AULA 5 Gabarito 1. a) (x + 3)(y + 1) f) (3x − y)(x + 3y) b) (x + y)(x − y) g) ((x2 )2 + 1)(x2 + 1)(x + 1)(x − 1) c) (5x + 2y)(5x − 2y) h) a2 b2 c2 (10bc2 − 15ac2 − 34a2 b) d) (6m + 10n)(6m − 10n) i) (n − 1)(m − 1) e) (11 + 13ab)(11 − 13ab) j) (y 2 + 4)(y + 2)(y − 2) b+1 a−b 2. a) b) a−1 a−1 3. a) 2x(2x + 3y + 1) f) 2xy 3 (x − 4y)2 b) (a − b)(a − b + 2) g) (25 + x − 3y)(25 − x + 3y) c) (a − x)(2b − c) h) x2 + y 2 x4 − x2 y 2 + y 4 d) 7x2 y − 1 (6x − 10) i) (2a − 1) 4a2 + 2a + 1 e) (4x + 6)(4x − 6) j) (a − b)3 d−e ax − 1 x+y 4. a) b) c) m−n y x−1 a+b x2 + 1 d) a − b e) f) 2 5 x −1 2 2 a − 2ab + b a+b g) a − 3 h) 2 i) a + ab + b2 a−b 5. 34 6. 1 75 CEDERJ
- 79. Equa¸˜o do 1o Grau ca ´ MODULO 1 - AULA 6 Aula 6 – Equa¸˜o do 1o Grau ca Senten¸a Aberta e Equa¸˜o c ca Vamos analisar as seguintes senten¸as: c 3 · 5 − 1 = 17 (6.1) 3 · 6 − 1 = 17 (6.2) 3 · x − 1 = 17 (6.3) Observe que: A senten¸a (6.1) ´ falsa pois 3 · 5 − 1 = 14 = 17 c e A senten¸a (6.2) ´ verdadeira pois 3 · 6 − 1 = 18 − 1 = 17 c e A senten¸a (6.3) n˜o ´ verdadeira nem falsa, pois x, chamado vari´vel, c a e a pode assumir qualquer valor. Esse ultimo tipo ´ um exemplo de senten¸a aberta. Toda senten¸a aberta, ´ e c c onde aparece uma vari´vel real, na forma de igualdade ´ chamada de equa¸˜o. a e ca Substituindo x por 6, a senten¸a aberta 3 · x − 1 = 17 se transforma em c 3 · 6 − 1 = 17 que ´ uma senten¸a verdadeira. Nesta situa¸˜o x = 6 ´ e c ca e uma raiz (ou uma solu¸˜o) da equa¸˜o, uma vez que para este valor de x, ca ca 3 · x − 1 = 17. Raiz e Conjunto-Verdade Raiz (ou solu¸˜o) de uma equa¸˜o ´ um n´ mero que transforma a ca ca e u senten¸a aberta em senten¸a verdadeira. Conjunto-Verdade ou Conjunto- c c Solu¸˜o de uma equa¸˜o ´ o conjunto de todas as ra´ ca ca e ızes. Resolver uma equa¸˜o ´ determinar o seu Conjunto-Verdade. ca e Equa¸˜o do 1o Grau ca Equa¸˜o do 1o Grau ´ toda senten¸a aberta em uma vari´vel real x, ca e c a que pode ser expressa na forma ax + b = 0, onde a e b s˜o n´ meros reais e a u a = 0. Vamos determinar o Conjunto-Solu¸˜o da equa¸˜o ax + b = 0: ca ca b ax + b = 0 ⇔ ax = −b ⇔ x = − , a = 0 . a b Portanto, o Conjunto-Solu¸˜o de ax + b = 0, com a = 0 ´ V = {− a }. ca e 77 CEDERJ
- 80. Equa¸˜o do 1o Grau ca Exemplo 1 a) O n´ mero 2 ´ raiz da equa¸˜o 4x − 1 = 7, pois substituindo x por 2 a u e ca senten¸a aberta 4x − 1 = 7 se transforma em 4 · 2 − 1 = 7 que ´ uma c e senten¸a verdadeira. c b) O n´ mero 5 n˜o ´ raiz da equa¸˜o 4x − 1 = 7, pois substituindo x por u a e ca 5 a senten¸a aberta 4x − 1 = 7 se transforma em 4 · 5 − 1 = 7 que ´ c e uma senten¸a falsa. c c) O conjunto solu¸˜o V da equa¸˜o 3x − 18 = 0 ´ V = {6}. De fato, ca ca e 3x − 18 = 0 se, e somente se, x = 6. d) O conjunto solu¸˜o da equa¸˜o 3x + 2 = 3x − 1 ´ ∅, pois ca ca e 3x + 2 = 3x − 1 ⇔ 0x = −3 ⇔ 0 = −3 que ´ uma senten¸a falsa. e c e) Qual ´ o conjunto solu¸˜o V da equa¸˜o 3x − 6 = 3(x − 2)? e ca ca Solu¸˜o: ca 3x − 6 = 3x − 6 ⇔ 0x = 0 . Note que 0x = 0 ´ uma senten¸a verdadeira seja qual for x ∈ R. e c Portanto, V = R. 3x x + 1 f) Resolver a equa¸˜o ca − = 1. 4 3 Solu¸˜o: ca 3x x + 1 9x − 4(x + 1) 12 16 − =1⇔ = ⇔ 9x−4x−4 = 12 ⇔ 5x = 12+4 ⇔ x = . 4 3 12 12 5 16 Da´ o conjunto solu¸˜o V , da equa¸˜o ´ V = ı, ca ca e . 5 Aplica¸˜es da Equa¸˜o do 1o Grau co ca Exemplo 2 A soma de quatro n´ meros inteiros e consecutivos ´ 38. Achar esses n´ meros. u e u Solu¸˜o: ca Considere os n´ meros x, x + 1, x + 2 e x + 3. Ent˜o: u a x + x + 1 + x + 2 + x + 3 = 38 ⇔ 4x = 38 − 6 ⇔ x = 8 . Logo, os n´ meros s˜o: 8, 9, 10 e 11. u a CEDERJ 78
- 81. Equa¸˜o do 1o Grau ca ´ MODULO 1 - AULA 6 Exemplo 3 A idade de uma pessoa ´ o dobro da de outra. H´ cinco anos a soma das e a idades das duas pessoas era igual ` idade atual da mais velha. Quais s˜o as a a idades atuais das duas pessoas? Solu¸˜o: ca Sejam x a idade da pessoa mais nova. Portanto, 2x a idade da mais velha. Usando dados de cinco anos atr´s encontramos que a x − 5 + 2x − 5 = 2x ⇔ x = 10 e 2x = 20 . Logo, as idades atuais s˜o 10 anos e 20 anos. a Exerc´ ıcios Propostos 1. Resolva em R, a equa¸˜o 3x − 27 = 0. ca 2. Resolva em R, a equa¸˜o 12 + 4x = 0. ca 3. Resolva em R, a equa¸˜o x[2x − (3 − x)] − 3 x2 − 1 = 0. ca 4. Resolva em R, a equa¸˜o 3x + 1 = 3x + 4. ca 5. Resolva em R, a equa¸˜o 5(x − 1) = 5x − 5. ca 5x − 1 x 142 6. Resolva em R, a equa¸˜o ca − = . 2 3 15 4x − 2 1 1 − 4x 7. Resolva em R, a equa¸˜o ca − =2− . 5 10 2 8. A soma de cinco n´ meros ´ u ımpares e consecutivos ´ 905. Quais s˜o esses e a n´ meros? u 9. A soma de dois n´ meros ´ 200. Ache-os sabendo que a metade de um u e 3 ´ igual a 4 do outro. e 10. A diferen¸a entre dois n´ meros ´ 18. Somando 4 a ambos, o maior c u e torna-se o qu´druplo do menor. Determine os dois n´ meros. a u Gabarito 1. V = {9} 6. V = { 23 } 5 2. V = {−3} 7. V = {− 5 } 3 3. V = {1} 8. 177, 179, 181, 183 e 185 4. V =∅ 9. 120 e 80 5. V =R 10. 20 e 2 79 CEDERJ
- 83. Sistemas de Equa¸oes do 1o Grau c˜ ´ MODULO 1 - AULA 7 Aula 7 – Sistemas de Equa¸˜es do 1o Grau co Considere numa situa¸˜o um pouco mais geral, as situa¸˜es abertas ca co x+y = 8 (7.1) x−y =4 (7.2) onde x e y s˜o n´ meros reais. N˜o ´ poss´ decidir se (7.1) ou (7.2) s˜o a u a e ıvel a verdadeiras ou falsas. No entanto, observe que: x=1 x=7 x=6 x=2 ; ; ; y=7 y=1 y=2 y=6 s˜o algumas das solu¸˜es da equa¸˜o x + y = 8. Da mesma forma a co ca x=7 x=6 x=5 x=8 ; ; ; y=3 y=2 y=1 y=4 s˜o algumas das solu¸˜es da equa¸˜o x − y = 4. Repare que x = 6 e y = 2 ´ a co ca e solu¸˜o de ambas as equa¸˜es x + y = 8 e x − y = 4. Da´ que x = 6 e y = 2 ca co ı, ´ solu¸˜o do sistema e ca x+y =8 x−y = 4 Uma solu¸˜o de um sistema de duas equa¸˜es e duas inc´gnitas x e y ´ ca co o e qualquer par ordenado (x, y) que satisfaz as duas equa¸˜es. co Defini¸˜o 1 ca Se a, b e c s˜o n´ meros reais, com a = 0 e b = 0, a equa¸˜o a u ca ax + by = c , ´ dita uma equa¸˜o do primeiro grau com duas inc´gnitas. e ca o Nota: 1. Conforme visto acima, uma equa¸˜o do primeiro grau possui muitas ca solu¸˜es. co 2. Um conjunto de duas equa¸˜es do primeiro grau, isto ´, um sistema de co e duas equa¸˜es do primeiro grau possui uma unica solu¸˜o em x e y ou co ´ ca n˜o possui solu¸˜o ou possui infinitas solu¸˜es. a ca co 81 CEDERJ
- 84. Sistemas de Equa¸oes do 1o Grau c˜ Vamos agora aprender dois m´todos para achar solu¸˜es de um sistema e co de duas equa¸˜es com duas inc´gnitas. co o M´todo da Substitui¸˜o e ca Exemplo 1 2x + 5y = 1 Determine o conjunto solu¸˜o do sistema ca . 3x + 2y = −4 Solu¸˜o: ca A partir da equa¸˜o 2x+5y = 1, vamos “isolar”, por exemplo, a vari´vel ca a y, isto ´: e 1 − 2x 2x + 5y = 1 ⇔ y = . 5 Substituindo o valor de y na equa¸˜o 3x + 2y = −4 temos que ca 1 − 2x 3x + 2 = −4 ⇔ 15x + 2 − 4x = −20 ⇔ 11x = −22 ⇔ x = −2 . 5 Logo, 1 − 2(−2) y= ⇔ y = 1. 5 Portanto, x = −2 e y = 1 ou V = {(−2, 1)} ´ o conjunto solu¸˜o. e ca M´todo da Adi¸˜o e ca 2x + 5y = 1 Determine o conjunto solu¸˜o do sistema ca . 3x + 2y = −4 Solu¸˜o: ca Multiplicando a primeira equa¸˜o por 2 e a segunda equa¸ao por -5, e ca c˜ em seguida adicionando as equa¸˜es encontramos que, co 4x + 10y = 2 + −15x − 10y = 20 −11x + 0y = 22 . Portanto, −11x = 22 o que implica x = −2. Substituindo x = −2 em qualquer das duas equa¸˜es iniciais temos que co 2(−2) + 5y = 1 ⇔ y = 1 . Da´ x = −2 e y = 1 ou V = {(−2, 1)} ´ o conjunto solu¸˜o. ı, e ca Veja mais um exemplo usando o m´todo da substitui¸˜o: e ca CEDERJ 82
- 85. Sistemas de Equa¸oes do 1o Grau c˜ ´ MODULO 1 - AULA 7 Exemplo 2 x + 3y = 4 Resolver o sistema . 2x − y = 1 Solu¸˜o: ca A partir da primeira equa¸˜o x + 3y = 4 “isolamos”, por exemplo, a ca vari´vel y, isto ´: a e 4−x x + 3y = 4 ⇔ y = . 3 Substituindo este resultado na equa¸˜o em 2x − y = 1 temos que ca 4−x 2x − = 1 ⇔ 6x − 4 + x = 3 ⇔ 7x = 7 ⇔ x = 1 . 3 Logo, 4−1 y= = 1. 3 Portanto, x = 1 e y = 1 ou V = {(1, 1)} ´ a solu¸˜o do sistema de equa¸˜es. e ca co Exerc´ ıcios Propostos 2x − y = 1 1. Resolva o sistema . 3x + 2y = 5 x − 4y = 5 2. Resolva o sistema . 3x + y = 2 3. Num s´ existem patos e porcos, num total de 40 cabe¸as e 128 p´s. ıtio c e Determine o n´ mero de porcos desse s´ u ıtio. 4. H´ cinco anos a idade de Pedro era o dobro da idade de Joana. Daqui a a cinco anos a soma das duas idades ser´ de 65 anos. Quantos anos a Pedro ´ mais velho que Joana? e 5. O IBGE contratou um certo n´ mero de entrevistadores para realizar o u recenseamento em uma certa cidade. Se cada um deles recenseasse 100 residˆncias, 60 delas n˜o seriam visitadas. Como, no entanto, todas e a as residˆncias foram visitadas e cada recenseador visitou 102, quantas e residˆncias tem a cidade? e Gabarito 1. V = {(1, 1)} 2. V = {(1, −1)} 3. 24 4. 15 5. 3060 83 CEDERJ
- 87. Equa¸˜o do 2o Grau ca ´ MODULO 1 - AULA 8 Aula 8 – Equa¸˜o do 2o Grau ca Defini¸˜o ca Defini¸˜o 1 ca Equa¸˜o do 2o Grau ´ toda equa¸˜o da forma ax2 +bx+c = 0, ca e ca onde a, b, c ∈ R, com a = 0. Nota: Repare que a = 0 ´ fundamental na defini¸˜o da equa¸˜o do 2o grau. e ca ca 2 De fato, se a = 0, ent˜o ax + bx + c = 0 ´ reduzida ` equa¸˜o bx + c = 0 a e a ca que ´ uma equa¸˜o do 1o grau (na hip´tese em que b = 0). e ca o Exemplo 1 a) Na equa¸˜o 7x2 + x − 1 = 0 temos a = 7, b = 1 e c = −1. ca b) Na equa¸˜o x2 − x − 1 = 0 temos a = 1, b = −1 e c = −1. ca c) Na equa¸˜o x2 − 10x = 0 temos a = 1, b = −10 e c = 0. ca d) Na equa¸˜o x2 − 25 = 0 temos a = 1, b = 0 e c = −25. ca Resolu¸˜o de uma Equa¸˜o do 2o Grau (M´todo de ca ca e Baskara) Uma equa¸˜o do 2o grau ax2 + bx + c = 0, onde a, b, c ∈ R, com ca a = 0, possui no m´ximo duas ra´ a ızes. Vamos estabelecer um procedimento para encontrar essas ra´ızes. O m´todo de Baskara consiste em completar e quadrados para isolar a inc´gnita x. Veja como funciona passo-a-passo. o 1o passo: Vamos multiplicar a equa¸˜o por 4a: ca 4a ax2 + bx + c = 4a(0) ⇔ 4a2 x2 + 4abx + 4ac = 0 . 2o passo: Vamos somar b2 aos dois membros da igualdade: 4a2 x2 + 4abx + 4ac + b2 = 0 + b2 ⇔ 4a2 x2 + 4abx + 4ac + b2 = b2 . 85 CEDERJ
- 88. Equa¸˜o do 2o Grau ca 3o passo: Neste ultimo passo vamos manipular algebricamente a equa¸˜o ´ ca obtida no passo anterior: 4a2 x2 + 4abx + 4ac + b2 = b2 ⇔ 4a2 x2 + 4abx + b2 = b2 − 4ac ⇔ (2ax + b)2 = b2 − 4ac √ ⇔ 2ax + b = ± b2 − 4ac √ −b ± b2 − 4ac ⇔ x= 2a A express˜o que acabamos de determinar para a raiz x da equa¸˜o ´ cha- a ca e 2 mada de solu¸˜o geral. O n´ mero ∆ = b − 4ac recebe a denomina¸˜o de ca u ca discriminante da equa¸˜o. ca Exemplo 2 a) Vamos achar as ra´ da equa¸˜o x2 − 7x + 6 = 0. ızes ca Solu¸˜o: ca Temos que a = 1, b = −7 e c = 6. Ent˜o: a √ −(−7) ± (−7)2 − 4 × 1 × 6 7 ± 25 7±5 x= = = ⇒ x = 1 ou x = 6 . 2×1 2 2 Portanto, S = {1, 6} ´ o conjunto solu¸˜o da equa¸˜o. e ca ca b) Vamos achar as ra´ da equa¸˜o x2 + 11x + 28 = 0. ızes ca Solu¸˜o: ca Temos que a = 1, b = 11 e c = 28. Ent˜o: a √ −11 ± (11)2 − 4 × 1 × 28 −11 ± 9 −11 ± 3 x= = = ⇒ x = −7 ou x = −4 . 2×1 2 2 Portanto, S = {−7, −4} ´ o conjunto solu¸˜o da equa¸˜o. e ca ca Obs.: 1) Se a, b e c s˜o reais n˜o-nulos, ent˜o, a equa¸˜o ax2 + bx + c = 0, diz-se a a a ca completa. 2) Se pelo menos um dos n´ meros reais b ou c ´ nulo, ent˜o, a equa¸˜o u e a ca 2 o ax +bx+c = 0 diz-se incompleta. Uma equa¸˜o do 2 grau incompleta ca pode ser resolvida diretamente, sem passar pela f´rmula geral. Vamos o tratar estes casos. CEDERJ 86
- 89. Equa¸˜o do 2o Grau ca ´ MODULO 1 - AULA 8 Equa¸˜es Incompletas co 1o caso: b = 0. Neste caso, a equa¸˜o ax2 + bx + c = 0 se torna ax2 + c = 0. Portanto, ca a solu¸˜o pode ser obtida: ca c c ax2 + c = 0 ⇐⇒ ax2 = −c ⇐⇒ x2 = − ⇐⇒ x = ± − . a a c Repare que na situa¸˜o que − > 0, a equa¸˜o admite duas ra´ sim´tricas. ca ca ızes e a c No caso em que − < 0, a equa¸˜o n˜o possui solu¸˜o real. ca a ca a Exemplo 3 a) Resolvendo a equa¸˜o 4x2 − 16 = 0 temos: ca 16 4x2 − 16 = 0 ⇔ 4x2 = 16 ⇔ x2 = ⇔ x2 = 4 ⇔ x = ±2 . 4 Da´ S = {−2, 2} ´ o conjunto solu¸˜o. ı, e ca b) Resolvendo a equa¸˜o 2x2 − 36 = 0 temos: ca 36 √ 2x2 − 36 = 0 ⇔ 2x2 = 36 ⇔ x2 = ⇔ x2 = 18 ⇔ x = ±3 2 . 2 √ √ Da´ S = {−3 2, 3 2} ´ o conjunto solu¸˜o. ı, e ca c) Resolvendo a equa¸˜o 3x2 + 12 = 0 temos: ca −12 √ 3x2 + 12 = 0 ⇔ 3x2 = −12 ⇔ x2 = ⇔ x2 = −4 ⇔ x = ± −4 . 3 Da´ S = ∅, ou seja, a equa¸˜o n˜o possui solu¸˜o nos n´ meros reais. ı, ca a ca u 2o caso: c = 0. Neste caso, a equa¸˜o ax2 +bx+c = 0 se torna ax2 +bx = 0. Resolvendo ca diretamente encontramos que: ax2 + bx = 0 ⇔ x(ax + b) = 0 ⇔ x = 0 ou ax + b = 0 ⇔ x = 0 ou ax = −b ⇔ b ⇔ x = 0 ou x = − . a b Portanto, uma das ra´ ´ sempre nula e a outra ´ da forma − a . ızes e e Exemplo 4 a) Resolvendo a equa¸˜o 6x2 − 8x = 0 temos: ca 4 6x2 − 8x = 0 ⇔ 2x(3x − 4) = 0 ⇔ 2x = 0 ⇔ x = 0 ou 3x − 4 = 0 ⇔ x = . 3 4 Da´ S = {0, 3 } ´ o conjunto solu¸˜o da equa¸˜o. ı, e ca ca 87 CEDERJ
- 90. Equa¸˜o do 2o Grau ca b) Resolvendo a equa¸˜o x2 − 7x = 0 temos que ca x2 − 7x = 0 ⇔ x(x − 7) = 0 ⇔ x = 0 ou x − 7 = 0 ⇔ x = 7 . Da´ S = {0, 7} ´ o conjunto solu¸˜o da equa¸˜o. ı, e ca ca Discuss˜o Sobre Existˆncia e N´ mero de Ra´ a e u ızes As ra´ da equa¸˜o do 2o grau s˜o obtidas pela f´rmula ızes ca a o √ −b ± ∆ x= , onde ∆ = b2 − 4ac . 2a Portanto, Se ∆ < 0 ent˜o a equa¸˜o n˜o tem ra´ reais; a ca a ızes Se ∆ = 0 ent˜o a equa¸˜o tem duas ra´ reais e iguais; a ca ızes Se ∆ > 0 ent˜o a equa¸˜o tem duas ra´ reais e distintas. a ca ızes Exemplo 5 a) Na equa¸˜o 9x2 + 6x + 1 = 0 temos que ca ∆ = 36 − 36 = 0 . Assim, sem resolver a equa¸˜o dada, podemos afirmar que ela possui ca duas ra´ reais e iguais pois ∆ = 0. ızes b) Na equa¸˜o x2 + x + 4 = 0 temos que ca ∆ = 1 − 16 = −15 . Assim, sem resolver a equa¸˜o dada, podemos afirmar que ela n˜o ca a possui ra´ reais pois ∆ < 0. ızes Rela¸˜o entre os Coeficientes e as Ra´ ca ızes de uma Equa¸˜o do 2o Grau ca Sabemos que as ra´ da equa¸˜o ax2 + bx + c = 0 s˜o dadas por ızes ca a √ √ −b − ∆ −b + ∆ x1 = ou x2 = , onde ∆ = b2 − 4ac . 2a 2a CEDERJ 88
- 91. Equa¸˜o do 2o Grau ca ´ MODULO 1 - AULA 8 Assim, Soma (S = x1 + x2 ) das Ra´ ızes Usando os resultados anteriores obtemos que √ √ −b − ∆ −b + ∆ −2b b S = x1 + x2 = + = =− . 2a 2a 2a a Logo, b S=− . a Produto (P = x1 · x2 ) das Ra´ ızes Usando os resultados anteriores obtemos que √ √ −b − ∆ −b + ∆ b2 − ∆ b2 − b2 − 4ac 4ac c P = x1 ·x2 = · = 2 = 2 = 2 = . 2a 2a 4a 4a 4a a Logo, c P = . a Composi¸˜o da Equa¸˜o do 2o Grau ca ca O nosso objetivo ´ determinar um processo para a obten¸˜o de uma e ca o equa¸˜o do 2 grau conhecidas as suas ra´ ca ızes. Considere a equa¸˜o ca ax2 + bx + c = 0, onde a, b, c ∈ R e a = 0. Dividindo a equa¸˜o por a ca temos que ax2 bx c 0 b c + + = ⇔ x2 − − x + = 0. a a a a a a b c Como S = − e P = temos: a a x2 − Sx + P = 0 . Portanto, a partir da prescri¸˜o de dois n´ meros x1 e x2 , a equa¸˜o ca u ca 2 x − Sx + P = 0, admite estes n´ meros como ra´ desde que S = x1 + x2 u ızes e P = x1 · x2 . Exemplo 6 a) Calcule a soma e o produto das ra´ das equa¸˜o x2 − 8x + 20 = 0. ızes ca Solu¸˜o: ca Temos que: b (−8) c 20 S=− =− =8 e P = = = 20 . a 1 a 1 89 CEDERJ
- 92. Equa¸˜o do 2o Grau ca b) Calcule a soma e o produto das ra´ das equa¸˜o x2 + 18x − 25 = 0. ızes ca Solu¸˜o: ca Temos que: b 18 c −25 S=− =− = −18 e P = = = −25 . a 1 a 1 c) Calcule a soma e o produto das ra´ das equa¸˜o 3x2 − 54 = 0. ızes ca Solu¸˜o: ca Temos que: b 0 c −54 S=− =− =0 e P = = = −18 . a 3 a 3 d) Escreva a equa¸˜o do 2o grau cujas ra´ s˜o 4 e -8. ca ızes a Solu¸˜o: ca Temos que: S = 4 + (−8) = −4 P = 4 × (−8) = −32 . Usando a f´rmula x2 − Sx + P = 0 temos que o x2 + 4x − 32 = 0 . √ √ e) Escreva a equa¸˜o do 2o grau cujas ra´ s˜o 2 + ca ızes a 3 e 2− 3 . Solu¸˜o: ca Temos que: √ √ S =2+ 3+2− 3=4 √ √ P = (2 + 3) · (2 − 3) = 4 − 3 = 1 . Usando a f´rmula x2 − Sx + P = 0 temos que o x2 − 4x + 1 = 0 . Exerc´ ıcios Propostos 1. Se x ´ positivo e se o inverso de x + 1 ´ x − 1, determine o valor de x. e e b2 2 2. Determine a rela¸˜o entre a e b para que a equa¸˜o ca ca x + 1 + ax = 0 2 n˜o possua raiz real. a CEDERJ 90
- 93. Equa¸˜o do 2o Grau ca ´ MODULO 1 - AULA 8 3. Resolva as equa¸˜es: co a) 2x2 − 5x − 3 = 0 b) x2 − 6x + 8 = 0 c) x2 − 4x + 4 = 0 √ d) x2 + 3 2 x + 4, 5 = 0 4. Determine m para que a equa¸˜o 3x2 + (5m − 2)x + m − 1 = 0 admita ca ra´ sim´tricas. ızes e 5. Determine o valor de m para que o produto das ra´ ızes da equa¸˜o ca 2 5x − 8x + 2m − 1 = 0 seja igual a 20. 6. Determine a m´dia aritm´tica das ra´ da equa¸˜o e e ızes ca x2 − (p − m)x + 3p − 4m = 0 . 7. Determine os valores de k para os quais a equa¸˜o ca (2k − 3)x2 − (5k + 6)x + k + 4 = 0 . a) Tenha ra´ sim´tricas ızes e b) Tenha uma s´ raiz nula o 8. Determine o valor de m de modo que o n´ mero 3 seja uma das ra´ u ızes 2 da equa¸˜o 2x − (4m + 1)x − m + 2 = 0. ca 9. Determine a equa¸˜o do 2o grau de ra´ ca ızes a) 6 e -4 √ √ b) 4 + 3 e 4 − 3 3 c) e -2 5 10. Resolva a equa¸˜o x2 − 3kx + 2k 2 = 0. ca 91 CEDERJ
- 94. Equa¸˜o do 2o Grau ca Gabarito √ 1. 2 2. a2 < b2 √ 3. a) S = {3, − 2 } b) S = {2, 4} c) S = {2} d) S = { −32 2 } 1 2 4. m = 5 5. m = 1012 6. p−m 2 6 7. a) k = − 5 b) k = −4 17 8. m = 13 9. a) x2 − 2x − 24 = 0 b) x2 − 8x + 13 = 0 c) 5x2 + 7x − 6 = 0 10. S = {k, 2k} CEDERJ 92
- 95. Inequa¸˜o do 1o Grau ca ´ MODULO 1 - AULA 9 Aula 9 – Inequa¸˜o do 1o Grau ca Defini¸˜o ca Defini¸˜o 1 ca Chama-se inequa¸˜o do 1o grau na vari´vel x toda inequa¸˜o ca a ca que se reduz a uma das formas ax + b ≥ 0, ax + b > 0, ax + b ≤ 0 ou ax + b < 0, onde a e b s˜o n´ meros reais a u quaisquer com a = 0. Nota: Defini¸˜es equivalentes podem ser formuladas para inequa¸˜es do co co 2o grau e sistemas de inequa¸˜es. Por exemplo, co 2x − 3 < 0 5x + 1 ≥ 0 ´ um sistema de inequa¸˜es do primeiro grau. Por outro lado, e co x2 − 5x + 2 ≤ 0 ´ uma inequa¸˜o do segundo grau. e ca Resolver uma inequa¸˜o do primeiro grau ´ encontrar todos os n´ meros ca e u reais x que satisfazem a desigualdade. A solu¸˜o pode ser obtida com auxilio ca de propriedades conhecidas de n´ meros reais. Veja a seguir algumas dessas u propriedades: Se x e y s˜o n´ meros reais, ent˜o a u a x < y ⇐⇒ x + a < y + a , ∀ a ∈ R; x < y ⇐⇒ xa < ya , ∀ a ∈ R , a > 0; x < y ⇐⇒ xa > ya , ∀ a ∈ R , a < 0. Propriedades equivalentes valem para os sinais ≤ , ≥ e >. Exemplo 1 Resolver a inequa¸˜o −3x + 9 ≥ 0 em R. ca Solu¸˜o: ca −3x + 9 ≥ 0 ⇔ −3x ≥ −9 ⇔ 3x ≤ 9 ⇔ x ≤ 3 . Logo, o conjunto solu¸˜o ´ S = {x ∈ R | x ≤ 3}. ca e 93 CEDERJ
- 96. Inequa¸˜o do 1o Grau ca Exemplo 2 Resolver a inequa¸˜o 3(2x − 1) − 4(x − 2) ≥ 3 em R. ca Solu¸˜o: ca 3(2x − 1) − 4(x − 2) ≥ 3 6x − 3 − 4x + 8 ≥ 3 2x + 5 ≥ 3 2x ≥ −2 x ≥ −1 Logo, o conjunto solu¸˜o ´ S = {x ∈ R | x ≥ −1}. ca e Exemplo 3 Resolver a inequa¸˜o 1 < 3x − 5 < 10 em R. ca Solu¸˜o: ca Devemos resolver as inequa¸˜es 1 < 3x−5 e 3x−5 < 10, ou seja, temos co um sistemas de inequa¸˜es, co 1 < 3x − 5 3x − 5 < 10 . Resolvendo a primeira inequa¸˜o encontramos ca 1 < 3x − 5 ⇔ −3x < −5 − 1 ⇔ −3x < −6 ⇔ 3x > 6 ⇔ x > 2 . Podemos representar graficamente o conjunto solu¸˜o S1 desta inequa¸˜o. ca ca Veja a figura a seguir: S1 2 Para a segunda equa¸˜o temos que ca 3x − 5 < 10 ⇔ 3x < 10 + 5 ⇔ 3x < 15 ⇔ x < 5 . Representando o conjunto solu¸˜o S2 sobre uma reta, encontramos ca S2 5 CEDERJ 94
- 97. Inequa¸˜o do 1o Grau ca ´ MODULO 1 - AULA 9 A interse¸˜o S1 ∩ S2 dessas duas solu¸˜es d´ a solu¸˜o S procurada. ca co a ca Veja a figura a seguir, S2 5 1111111111 0000000000 S1 2 111 000 S = S1 ∩ S2 2 5 O conjunto solu¸˜o ´ S = {x ∈ R | 2 < x < 5}. ca e Exerc´ ıcios 1. Resolva as inequa¸˜es do 1o grau em R: co a) 3(x − 8) − 5(x + 2) > 3 x+3 x−1 b) − ≥0 4 3 3x 2x c) − ≤1 5 3 d) −2 < 3x − 1 < 5 e) x < 3x − 4 < 2x + 5 Gabarito −37 a) {x ∈ R | x < 2 } b) {x ∈ R | x ≤ 13} c) {x ∈ R | x ≥ −15} 1 d) {x ∈ R | − 3 < x < 2} e) {x ∈ R | 2 < x < 9} Inequa¸˜o Produto ca Nesta se¸˜o vamos considerar caso simples de inequa¸˜o obtidas atrav´s ca ca e de produto de duas inequa¸˜es do primeiro grau. co Para isto, considere equa¸˜es do primeiro grau f (x) = 0 e g(x) = 0, co onde f (x) = ax + b e g(x) = cx + d . Vamos resolver inequa¸˜es produto do tipo co f (x)g(x) ≥ 0 , f (x)g(x) > 0 , f (x)g(x) ≤ 0 ou f (x)g(x) < 0 . A solu¸˜o de qualquer destas inequa¸˜es pode ser obtida atrav´s do ca co e estudo dos sinais de f (x) e g(x). Vamos ver como isto funciona atrav´s dos e exemplos a seguir. 95 CEDERJ
- 98. Inequa¸˜o do 1o Grau ca Exemplo 4 Resolver a inequa¸˜o (x + 3)(−2x + 4) ≥ 0. ca Solu¸˜o: ca Escrevendo f (x) = x + 3 e g(x) = −2x + 4 a inequa¸˜o se torna ca f (x) · g(x) ≥ 0. Estudaremos o sinal de f (x) e g(x). + + −3 2 Sinal de f (x) Sinal de g(x) Note que qualquer valor maior que -3, f (x) > 0 Note que qualquer valor maior que 2, g(x) < 0 e qualquer valor menor que -3, f (x) < 0. e qualquer valor menor que 2, g(x) > 0. Os valores divis´rios -3 para f (x) e 2 para g(x) s˜o obtidos resolvendo as o a equa¸˜es f (x) = 0 e g(x) = 0. Em seguida, para determinar o sinal (+) ou co (−) resolvemos as inequa¸˜es f (x) > 0, f (x) < 0, g(x) > 0 e g(x) < 0. co Vamos agora determinar o sinal do produto f (x)g(x): _ + + 1 0 f (x) 1 0 −3 _ g(x) + + 11 00 11 00 _ 2 _ 1 0 + 1 0 111111111 000000000 f (x)g(x) 1 0 1 0 −3 2 Uma vez que estamos resolvendo a inequa¸˜o f (x)g(x) ≥ 0 encontramos ca S = {x ∈ R | −3 ≤ x ≤ 2} , como o conjunto solu¸˜o. ca Exemplo 5 Resolver a inequa¸˜o x(−2x + 6)(x − 2) < 0. ca Solu¸˜o: ca Escrevendo f (x) = x, g(x) = −2x + 6 e h(x) = x − 2, a inequa¸˜o se ca torna f (x)g(x)h(x) < 0. Estudando os sinais encontramos: _ + + _ _ + 0 3 2 x=0 −2x + 6 = 0 ⇒ x = 3 x−2=0⇒x=2 CEDERJ 96
- 99. Inequa¸˜o do 1o Grau ca ´ MODULO 1 - AULA 9 Vamos agora determinar o sinal do produto f (x)g(x)h(x): _ 0 + + + f (x) _ _ 2 g(x) + + h(x) + + + 3 _ _ + 000000 _ + 0000 111111 1111 f (x)g(x)h(x) 0 2 3 Uma vez que estamos resolvendo a inequa¸˜o f (x)g(x)h(x) < 0, encontra- ca mos: S = {x ∈ R | 0 < x < 2 ou x > 3} , como o conjunto solu¸˜o. ca Exerc´ ıcios 1. Resolva as inequa¸˜es do 1o grau em R: co a) (x + 1)(x − 5) > 0 b) (−x − 1)(3x − 5) < 0 c) (x − 1)(−x + 3)(x − 2) < 0 d) 2x(3x + 1)(−x + 2) ≤ 0 Gabarito 5 a) {x ∈ R | x < −1 ou x > 5} b) {x ∈ R | x < −1 ou x > 3 } 1 c) {x ∈ R | 1 < x < 2 ou x > 3} d) {x ∈ R | − 3 ≤ x ≤ 0 ou x ≥ 2} Inequa¸˜o Quociente ca Na mesma linha das inequa¸˜es produto que acabamos de estudar, va- co mos tratar o caso de inequa¸˜es onde aparecem quociente do tipo co f (x) f (x) f (x) f (x) ≥ 0, > 0, ≤ 0 ou < 0, g(x) g(x) g(x) g(x) onde f (x) = ax + b e g(x) = cx + d, com a = 0 e c = 0. Iremos encontrar o conjunto solu¸˜o S destas inequa¸˜es no conjunto ca co dos n´ meros reais. No entanto, temos um problema! Nas inequa¸˜es apa- u co rece como denominador g(x) = cx + d, c = 0. Ora, a inequa¸˜o n˜o tem ca a 97 CEDERJ
- 100. Inequa¸˜o do 1o Grau ca d sentido quando g(x) = 0. Isto ocorre quando x = − . Para contornar esta c dificuldade procuraremos o conjunto solu¸˜o S da inequa¸˜o de modo que ca ca d S⊂ x∈R|x=− . c Como a regra de sinais para o quociente ´ similar ` regra de sinais para e a o produto, para resolvermos uma inequa¸˜o quociente o procedimento segue ca a linha daquele usado na resolu¸˜o da inequa¸˜o produto.Aqui ´ necess´rio ca ca e a observar o cuidado extra que g(x) = 0. Exemplo 6 3x − 6 Resolver a inequa¸˜o ca > 0. x−3 Solu¸˜o: ca Temos que: _ 2 + + _ _ 3 + 3x − 6 = 0 ⇒ x = 2 + _ + 11111 00000 1111111 0000000 x−3 =0 ⇒x= 3 2 3 Observando as representa¸˜es dos sinais concluimos que co S = {x ∈ R | x < 2 ou x > 3} ´ o conjunto solu¸˜o da inequa¸˜o. e ca ca Exemplo 7 3x − 6 Resolver a inequa¸˜o ca ≥ 0. x−3 Solu¸˜o: ca A solu¸˜o ´ idˆntica ao exemplo anterior com a diferen¸a de que o ca e e c n´ mero x = 2 que anula o numerador deve ser acrescentado ao conjunto u solu¸˜o. Logo, S = {x ∈ R | x ≤ 2 ou x > 3}. ca Exemplo 8 3x − 4 Resolver a inequa¸˜o ca ≤ 1. x−3 Solu¸˜o: ca Temos que: 3x − 4 3x − 4 3x − 4 − x + 3 2x − 1 ≤1⇔ −1≤0⇔ ≤0⇔ ≤ 0. x−3 x−3 x−3 x−3 CEDERJ 98
- 101. Inequa¸˜o do 1o Grau ca ´ MODULO 1 - AULA 9 Assim, podemos representar graficamente os sinais. _ 1/2 + + _ _ 3 + + _ + 1 01111111 0000000 1 0 1/2 3 1 1 Note que 2 ´ solu¸˜o. Logo, S = {x ∈ R | e ca 2 ≤ x < 3}. Exerc´ ıcios 1. Resolva as seguintes inequa¸˜es: co x+3 a) <0 x+5 x b) ≤0 −x + 3 x+3 c) <1 x−1 x+5 d) <2 3x − 4 Gabarito a) {x ∈ R | −5 < x < −3} b) {x ∈ R | x ≤ 0 ou x > 3} 4 13 c) {x ∈ R | x < 1} d) {x ∈ R | x < 3 ou x > 5 } Inequa¸˜o Potˆncia ca e Encerrando nosso breve estudo de inequa¸˜es vamos colocar em desta- co que inequa¸˜es do tipo co [f (x)]n ≥ 0 , [f (x)]n > 0 , [f (x)]n ≤ 0 ou [f (x)]n < 0 , onde f (x) = ax + b, a = 0 e n > 1 ´ um n´ mero natural. e u Exemplo 9 Resolver as inequa¸˜es (3x − 6)6 ≥ 0, (3x − 6)6 > 0, (3x − 6)6 < 0 co 6 e (3x − 6) ≤ 0 99 CEDERJ
- 102. Inequa¸˜o do 1o Grau ca Solu¸˜o: ca Como n = 6 (par), ent˜o a potˆncia (3x − 6)6 nunca ser´ negativa. Ela a e a ser´ positiva se 3x − 6 = 0 e nula se 3x − 6 = 0. Em vista disso podemos a escrever o conjunto solu¸˜o S para cada inequa¸˜o: ca ca (3x − 6)6 ≥ 0 ⇒ S = R (3x − 6)6 > 0 ⇒ S = R − {2} (3x − 6)6 < 0 ⇒ S = ∅ (3x − 6)6 ≤ 0 ⇒ S = {2} Exemplo 10 Resolva a inequa¸˜o (4x − 8)3 > 0. ca Solu¸˜o: ca A potˆncia de expoente ´ e ımpar tem sempre o sinal da base. Ent˜o: a (4x − 8)3 > 0 ⇔ 4x − 8 > 0 ⇔ x > 2 . Logo, S = {x ∈ R | x > 2} ´ o conjunto solu¸˜o. e ca Exemplo 11 Resolva a inequa¸˜o (3x − 7)101 < 0. ca Solu¸˜o: ca A solu¸˜o ´ idˆntica que no exemplo anterior, isto ´, a potˆncia de ca e e e e expoente ´ ımpar tem sempre o sinal da base. Ent˜o: a 7 (3x − 7)101 < 0 ⇔ 3x − 7 < 0 ⇔ x < . 3 7 Logo, S = {x ∈ R | x < 3 } ´ o conjunto solu¸˜o. e ca Exerc´ ıcios 1. Resolva as seguintes inequa¸˜es: co a) (7 − 3x)4 < 0 b) (2x − 1)100 ≥ 0 c) (x − 4)7 ≤ 0 d) (3x − 1)1001 ≥ 0 Gabarito 1 1. a) S = ∅ b) S = R c) {x ∈ R | x ≤ 4} d) {x ∈ R | x ≥ 3 } CEDERJ 100
- 103. Inequa¸˜o do 1o Grau ca ´ MODULO 1 - AULA 9 Exerc´ ıcios Propostos 1. Determine o menor inteiro que verifica a inequa¸˜o ca 3(4x − 2) − 2(5x − 3) ≤ 5(x + 1) . 2. Resolva a inequa¸˜o em R: x(x − 3)6 (3x − 12)5 < 0. ca 56 − 7x 3. Determine os valores de x ∈ Z que satisfa¸am a inequa¸˜o c ca ≥ 0. 5x − 37 x−1 4. Ache todos os n´ meros reais x que satisfa¸am u c < 2. 3−x −4 3 −1 5. Ache os valores reais de x para os quais vale a desigualdade + ≥ . x 2 x 2x − 7 6. Determine o n´ mero de solu¸˜es inteiras do sistema 3 ≤ u co ≤ 5. 3 10 7. Ache todos os n´ meros reais x que satisfa¸am x2 − 4 u c (x − 2)5 > 0. 4 8. Determine os valores reais x que satisfa¸am c ≤ 0. x−3 4−x 9. Determine os valores reais x que satisfa¸am c > 0. x+3 10. Determine o n´ mero de solu¸˜es inteiras da inequa¸ao −3 < x + 2 ≤ 4. u co c˜ Gabarito 1. − 1 2. {x ∈ R | 0 < x < 3 ou 3 < x < 4} 3. x = 8 7 4. {x ∈ R | x < 3 ou x > 3} 5. {x ∈ R | x < 0 ou x ≥ 2} 6. 4 7. {x ∈ R | x > 2} 8. {x ∈ R | x < 3} 9. {x ∈ R | −3 < x < 4} 10. 7 101 CEDERJ
- 105. Progress˜o Aritm´tica a e ´ MODULO 1 - AULA 10 Aula 10 – Progress˜o Aritm´tica a e Sequˆncias e Introdu¸˜o ca Uma sequˆncia de n´ meros reais, ou uma sequˆncia abreviadamente, ´ e u e e uma cole¸˜o enumer´vel de n´ meros reais escrita ordenadamente, ca a u (ai ) = a1 , a2 , a3 , · · · , an , · · · onde an ´ um n´ mero real qualquer com i ∈ N∗ . e u Na verdade, expressamos a sequˆncia infinita, atrav´s da inscri¸˜o de e e ca trˆs pontinhos · · · ` direita da sequˆncia. No entanto, tamb´m considera- e a e e remos sequˆncias finitas. Por exemplo, e 1, 3, 5, 7, 9, · · · e √ 1, −2, 3, π, 5, 2 s˜o respectivamente uma sequˆncia infinita e uma sequˆncia finita. a e e 1 a1 2 a2 3 a3 1 0 1 0 1 0 1 0 1 0 1 0 N∗ R ´ Nota: E necess´rio considerar tamb´m sequˆncias finitas do tipo a1 , a2 , · · · a e e · · · , ak . Neste caso, basta considerar o conjunto finito Ik = {1, 2, 3, · · · , k} e descrever as sequˆncias de n´ meros reais finitas como fun¸˜es f : Ik → R. e u co Exemplo 1 Escreva explicitamente os termos da sequˆncia an = (−1)n+1 para todo e ∗ n∈N . 103 CEDERJ
- 106. Progress˜o Aritm´tica a e Solu¸˜o: ca Temos que a1 = (−1)1+1 = (−1)2 = 1 2+1 3 a2 = (−1) = (−1) = −1 . . . Logo, (an ) = (a1 , a2 , a3 , ...) = (1, −1, 1, ...). Exemplo 2 Escreva explicitamente os termos da sequˆncia (an ) tal que a1 = 2 e e an+1 = an + 2n. Solu¸˜o: ca Observe que: a1 =2 a2 = a1+1 = a1 + 2 × 1 = 2 + 2 = 4 a3 = a2+1 = a2 + 2 × 2 = 4 + 4 = 8 a4 = a3+1 = a3 + 2 × 3 = 8 + 6 = 14 a5 = a4+1 = a4 + 2 × 4 = 14 + 8 = 22 . . . Logo, (an ) = (a1 , a2 , a3 , a4 , a5 , ...) = (2, 4, 8, 14, 22, ...). Classifica¸˜o das Sequˆncias ca e Tipos Especiais de Sequˆncias e • (an ) ´ estritamente crescente se an < an+1 , para todo n ∈ N∗ e • (an ) ´ crescente se an ≤ an+1 , para todo n ∈ N∗ e • (an ) ´ estritamente decrescente se an > an+1 , para todo n ∈ N∗ e • (an ) ´ decrescente se an ≥ an+1 , para todo n ∈ N∗ e • (an ) ´ constante se an = an+1 , para todo n ∈ N∗ e Exerc´ ıcios Propostos 1. Considere a sequˆncia (an ), onde an = 2n − 1. Fa¸a as contas e escreva e c os primeiros cinco termos da sequˆncia. e CEDERJ 104
- 107. Progress˜o Aritm´tica a e ´ MODULO 1 - AULA 10 2. Seja a sequˆncia (a1 , a2 , a3 , ...) cujo termo geral ´ dado por e e an = n + 2(n + 2). Determine os quatro primeiros termos. a1 = 20 3. Determine o 5o termo da sequˆncia definida por e 3an+1 = an , ∀n ∈ N∗ 4. A partir da sequˆncia e a1 = 1 × 9 + 2 = 11 a2 = 12 × 9 + 3 = 111 a3 = 123 × 9 + 4 = 1111 a4 = 1234 × 9 + 5 = 11111 . . . . . . 1234567 × 81 + 72 determine o valor da express˜o a . 11 Progress˜o Aritm´tica a e Defini¸˜o 1 ca Sejam a e r dois n´ meros reais. Chama-se Progress˜o Aritm´tica u a e (P.A.) ` sequˆncia (an ) tal que a e a1 = a , an+1 = an + r , ∀n ∈ N∗ ou seja, (an ) = (a , a + r , a + 2r , a + 3r , . . .) . O n´ mero real r chama-se raz˜o da P.A. Segue da defini¸˜o que: u a ca r = an+1 − an , ∀n ∈ N∗ . Assim, r = a2 − a1 = a3 − a2 = a4 − a3 = · · · Exemplo 3 Seja (an ) uma sequˆncia. Ent˜o: e a (an ) = (−10, −8, −6, −4, . . .) ´ uma P.A. de raz˜o 2 e a (an ) = (10, 8, 6, 4, . . .) ´ uma P.A. de raz˜o -2 e a (an ) = (10, 10, 10, 10, . . .) ´ uma P.A. de raz˜o 0 e a 105 CEDERJ
- 108. Progress˜o Aritm´tica a e Classifica¸˜o ca Se (an ) ´ uma P.A. ent˜o: e a • (an ) ´ estritamente crescente se r > 0 e • (an ) ´ estritamente decrescente se r < 0 e • (an ) ´ constante se r = 0 e Termo Geral de uma P.A. Seja uma P.A. (an ) = (a1 , a2 , a3 , a4 , . . .). Pela defini¸˜o de P.A. ca temos que: a2 = a1 + r a3 = a2 + r = a1 + r + r = a1 + 2r a4 = a3 + r = a1 + 2r + r = a1 + 3r . . . an = a1 + (n − 1)r Esta ultima express˜o traduz o e-n´simo termo da P.A. em fun¸˜o do ´ a e ca primeiro termo e da raz˜o. A f´rmula ´ chamada express˜o do termo geral. a o e a Exemplo 4 Na progress˜o aritm´tica (an ) = (3, 7, 11, . . .), determine o 10o termo. a e Solu¸˜o: ca Temos que a10 = a1 + (10 − 1)r. Como a1 = 3 e r = 4 obtemos: a10 = 3 + 9 × 4 = 39 . Logo, concluimos que o 10o termo ´ igual a 39. e Exemplo 5 Se as elei¸˜es para presidente continuarem a ocorrer a cada quatro anos, co ent˜o em que ano ocorrer´ a vig´sima elei¸˜o a partir de 2006? a a e ca Solu¸˜o: ca A P.A. (2006, 2010, 2014, . . .) tem como primeiro termo 2006 e raz˜o a igual a 4. Logo, a20 = a1 + 19r = 2006 + 19 × 4 = 2082 . Concluimos que a vig´sima elei¸˜o ser´ no ano de 2082. e ca a CEDERJ 106
- 109. Progress˜o Aritm´tica a e ´ MODULO 1 - AULA 10 Exerc´ ıcios Propostos 5. O 150o n´ mero ´ u ımpar positivo ´: e a) 151 b) 291 c) 301 d) 299 e) 399 6. Calcule a raz˜o de uma P.A. de 23 termos cujo primeiro termo ´ 8 e o a e ultimo termo ´ 74. ´ e 7. Sendo 47 o d´cimo termo de uma P.A. e 2,75 sua raz˜o, calcule o e a primeiro termo. a1 = 1 8. Na sequˆncia (an ) dada por e 4an + 1 em que n ´ um e an+1 = 4 n´ mero natural. Ent˜o a45 vale: u a 43 45 a) b) 13 c) d) 12 e) 15 4 4 9. Inserindo-se cinco n´ meros entre 18 e 96 de modo que a sequˆncia u e (18 , a2 , a3 , a4 , a5 , a6 , 96) seja uma progress˜o aritm´tica tem-se a e a3 igual a: a) 43 b) 44 c) 45 d) 46 e) 47 10. Seja A o conjunto dos 1993 primeiros n´ meros inteiros estritamente u positivos. Quantos m´ ltiplos inteiros de 15 pertencem ao conjunto A? u 11. As ra´ da equa¸˜o x4 − 10x2 + 9 = 0: ızes ca a) possuem soma igual a 10 b) est˜o em P.A., se colocadas em ordem crescente a c) est˜o em P.A. cujo produto ´ 3 a e √ d) possuem soma igual a 10 e) possuem soma igual a 102 Desafio: Qual a rela¸˜o dos coeficientes a, b e c da equa¸˜o ax4 +bx2 +c = 0 ca ca para que as ra´ estejam em P.A.? ızes 107 CEDERJ
- 110. Progress˜o Aritm´tica a e Propriedades de uma P.A. Termos Equidistantes dos Extremos Defini¸˜o 2 ca Considere os n primeiros termos de uma P.A. Dois termos s˜o cha- a mados equidistantes dos extremos se o n´ mero de termos que precede u um deles ´ igual ao n´ mero que sucede o outro. e u a1 · · · ap , · · · , ak · · · an . p−1 n−k Nota: Se ap e ak s˜o termos equidistantes em uma P.A. ent˜o: a a p − 1 = n − k =⇒ p + k = 1 + n . Propriedade 1 A soma de dois termos equidistantes dos extremos ´ igual ` soma dos e a extremos, isto ´, e ap + ak = a1 + an . De fato, ap = a1 + (p − 1)r ak = a1 + (k − 1)r an = a1 + (n − 1)r da´ ı, ap + ak = 2a1 + (p + k − 2)r = 2a1 + (n + 1 − 2)r = a1 + a1 + (n − 1)r = a1 + an . Propriedade 2 Cada termo de uma P.A. ´ a m´dia aritm´tica entre o termo anterior e e e e posterior. CEDERJ 108
- 111. Progress˜o Aritm´tica a e ´ MODULO 1 - AULA 10 Demonstra¸˜o: ca Seja a P.A. (a1 , a2 , a3 , . . . , ap−1 , ap , ap+1 , . . .). Ent˜o: a ap−1 = a1 + (p − 1 − 1)r = a1 + (p − 2)r ap+1 = a1 + (p + 1 − 1)r = a1 + p · r ap−1 + ap+1 = 2a1 + (2p − 2)r = 2a1 + 2(p − 1)r ap−1 + ap+1 = a1 + (p − 1)r = ap . 2 isto ´, e ap−1 + ap+1 ap = . 2 Exemplo 6 (a1 , −1 , a3 , 2 , a5 ) s˜o os cinco primeiros termos de uma P.A. Determine a a1 , a3 e a5 . Solu¸˜o: ca Usando a propriedade 2 temos: −1 + 2 1 a3 = =⇒ a3 = . 2 2 Logo, a1 + a3 1 5 −1 = =⇒ −2 = a1 + =⇒ a1 = − 2 2 2 a3 + a5 1 7 2 = =⇒ 4 = + a5 =⇒ a5 = . 2 2 2 Exerc´ ıcios Propostos 12. Se a, b e c, nesta ordem, s˜o termos consecutivos de uma P.A., ent˜o o a a valor de 2a − 3b + 2c ´ igual a : e a) a + c b) −b c) a d) b e) c 13. A m´dia aritm´tica de 50 n´ meros que s˜o termos consecutivos de uma e e u a P.A. ´ 100. Retirando-se dessa P.A. os 3o , 5o , 46o e 48o termos a m´dia e e aritm´tica dos 46 termos restantes ´: e e a) 100 b) um n´ mero menor que 100 u c) um n´ mero compreendido entre 100 e 4600 u 109 CEDERJ
- 112. Progress˜o Aritm´tica a e d) 5000 e) 4600 14. Assinale (V) ou (F) conforme as senten¸as sejam verdadeiras ou falsas. c Numa P.A. a soma do 7o com o 17o termo ´ 50. Pode-se afirmar que: e 1) ( ) A soma do 1o com o 23o termo ´ maior que 50 e 2) ( ) A soma do 9o com o 15o termo ´ menor que 50 e 3) ( ) O dobro do 12o termo ´ 50 e Soma dos Primeiros n Termos de uma P.A. Vamos considerar o seguinte problema: Achar a soma dos 100 primeiros termos da sequˆncia (1, 2, 3, . . .). e Solu¸˜o: ca Note que (1, 2, 3, . . .) ´ uma P.A. de raz˜o 1. Consideremos a soma duas e a vezes em ordem crescente e decrescente: S = 1 + 2 + 3 + ··· + 98 + 99 + 100 S = 100 + 99 + 98 + ··· + 3 + 2 + 1 2S = 101 + 101 + 101 + ··· + 101 + 101 + 101 logo, 100 × 101 2S = 100 × 101 =⇒ S = =⇒ S = 5050 . 2 Note acima a aplica¸˜o da propriedade 1. De um modo geral temos ca que: (a1 + an )n S= . 2 Exemplo 7 Qual a soma dos inteiros consecutivos 1 , 2 , 3 , · · · , 2004 , 2005? Solu¸˜o: ca Temos uma P.A. de a1 = 1 , r = 1 , n = 2005 e an = 2005. Logo, (1 + 2005) × 2005 S= = 2.011.015 . 2 CEDERJ 110
- 113. Progress˜o Aritm´tica a e ´ MODULO 1 - AULA 10 Exerc´ ıcios Propostos 15. A soma dos p primeiros n´ meros naturais ´ u ımpares ´ igual: e a) ao quadrado da metade de p b) ao cubo de p c) ao quadrado de p d) ` metade do quadrado de p a e) ao triplo de p 16. Sabendo que a soma dos nove primeiros termos de uma P.A. ´ 17.874, e o calcule o seu 5 termo. 17. Numa P.A. sabe-se que a14 = 3 e a16 = 11. Calcule a soma dos seus trinta primeiros termos. 18. A soma das fra¸˜es irredut´ co ıveis positivas menores do que 10, de deno- minador 4, ´: e a) 10 b) 20 c) 60 d) 80 e) 100 19. A soma dos n primeiros termos de uma P.A. infinita ´ dada por e 2 ∗ Sn = 4n − 6n para todo n ∈ N . Determine o primeiro termo e a raz˜o dessa P.A. a 20. Determine a soma dos n´ meros inteiros estritamente positivo menores u que 101 e que n˜o s˜o divis´ a a ıveis por 3. 21. Considere uma P.A. de cinco termos. A soma dos termos ´ 10 e a soma e do primeiro com o terceiro ´ -2. O produto da raz˜o pelo primeiro e a termo ´: e a) 6 b) -3 c) -12 d) -6 e) -15 ınimo de termos que devemos somar na P.A. 8 , 7 , 6 , 5 , · · · 22. Qual o n´ mero m´ u para obtermos soma negativa? 23. A soma dos n primeiros termos de uma P.A. ´ n(n − 2), qualquer que e o seja n. Determine o 5 termo desta progress˜o. a 24. A soma dos m´ ltiplos de 11 comprrendidos entre 1 e 1000 ´: u e a) 42000 b) 45045 c) 47500 d) 43045 e) 45450 111 CEDERJ
- 114. Progress˜o Aritm´tica a e Exerc´ ıcios Complementares 25. Os n´ meros a1 , a2 , a3 , · · · , an , · · · em que n ´ inteiro positivo, est˜o u e a relacionados por ap = ap−1 + 2, com p = 2 , 3 , 4 , · · · . Se a1 = 1, determine a57 . 26. Se o n´ mero 225 for dividido em trˆs partes, formando uma P.A., de u e maneira que a terceira parte excede ` primeira de 140. Essas partes a ser˜o: a a) primos entre si b) m´ ltiplos de 5 e 10 ao mesmo tempo u c) n´ meros cujo produto ´ 54375 u e d) m´ ltiplos de 5 e 3 ao mesmo tempo u e) indeterminados 27. Em uma P.A. de sete termos, de raz˜o k, retiramos o segundo, terceiro, a quinto e sexto termos. A sucess˜o restante ´ uma P.A. de raz˜o: a e a k k a) k b) 2k c) d) 3k e) 2 3 28. Numa P.A. tem-se que a15 − a5 = 5 e o primeiro termo ´ oito vezes a e raz˜o. Logo, o primeiro termo ´: a e 1 a) b) 1 c) 2 d) 3 e) 4 2 29. A soma dos n´ meros entre 0 e 101 n˜o divis´ u a ıveis por 5 ´: e a) 1000 b) 2000 c) 3000 d) 4000 e) 5000 30. A soma dos n primeiros termos de uma P.A. ´ n2 + 4n. Ent˜o, o termo e a geral dessa P.A. ´: e a) 5 + 2n b) 2n + 3 c) n + 4 d) 2n + 1 e) 2n − 3 1−n 2−n 3−n 31. A soma dos n primeiros elementos da seq¨ˆncia ue n , n , n , ··· ´ dado por: e 1 1−n 2n + 3 a) 0 b) c) d) e) n + 1 n 2 2 32. O valor de x da P.A (x , 2x + 1 , 5x + 7 , · · · ) ´: e 2 1 3 4 5 a) b) − c) d) − e) − 5 4 2 5 2 CEDERJ 112
- 115. Progress˜o Aritm´tica a e ´ MODULO 1 - AULA 10 33. Se numa P.A., am + an = ap + aq ent˜o: a a) m + n = p + q b) m − n = p − q c) mn = pq m p d) = n q e) m = n = p = q 34. A soma do 4o e 8o termos de uma P.A. ´ 20. O 31o termo ´ o dobro do e e 16o termo. A raz˜o dessa P.A. ´: a e a) 7 b) 2 c) 3 d) 4 e) 5 Gabarito dos Exerc´ ıcios Propostos 1. (1 , 3 , 7 , 15 , 31) 9. b 17. 270 2. (7 , 10 , 13 , 16) 10. 132 18. e 20 3. 11. b 19. a1 = −2 e r = 8 9 4. 9090909 12. d 20. 3367 5. d 13. a 21. c 6. r = 3 14. 1)F, 2)F, 3)V 22. 18 7. 22, 25 15. c 23. 7 8. d 16. 1986 24. b Gabarito dos Exerc´ ıcios Complementares 25. 113 30. b 26. c 31. c 27. d 32. e 28. e 33. a 29. d 34. b 113 CEDERJ
- 117. Progress˜o Geom´trica a e ´ MODULO 1 - AULA 11 Aula 11 – Progress˜o Geom´trica a e Introdu¸˜o ca Vamos continuar considerando tipos especiais de sequˆncias de n´ meros e u ´ reais. E o caso das progress˜es geom´tricas. o e Defini¸˜o 1 ca Sejam a e q dois n´ meros reais n˜o nulos. Chama-se Pro- u a gress˜o Geom´trica (P.G.) ` sequˆncia (an ) tal que a e a e a1 = a an+1 = an · q , ∀n ∈ N∗ . Portanto, (an ) = (a , aq , aq 2 , aq 3 , · · · ) . O n´ mero real q ´ chamado de raz˜o da P.G. u e a Nota: A progress˜o geom´trica definida acima ´ infinita. Com pequena a e e modifica¸˜o est˜o definidas P.G. finitas com n termos: a1 , a2 , · · · , an . ca a Segue da Defini¸˜o 1 que, se a1 = 0 e q = 0, ent˜o ca a an+1 q= , ∀n ∈ N∗ . an Assim, a2 a3 a4 q= = = = ··· a1 a2 a3 Exemplo 1 A P.G (an ) = (2 , 6 , 18 , · · · ) tem como primeiro termo a1 = 2 e raz˜o q = 3. a 115 CEDERJ
- 118. Progress˜o Geom´trica a e Classifica¸˜o das P.G’s ca Se (an ) ´ uma P.G. ent˜o: e a • (an ) ´ estritamente crescente se an < an+1 para todo n ∈ N∗ . As e 8 > a1 > 0 < e q>1 condi¸˜es para a P.G. ser estritamente crescente s˜o: co a > ou a1 < 0 e 0<q<1 : Exemplo 2 a) (an ) = (2 , 10 , 50 , · · · ) temos que a1 = 2 ; q = 5 3 b) (an ) = − 3 , − 2 , − 3 , · · · temos que a1 = −3 ; q = 4 1 2 • (an ) ´ estritamente decrescente se an > an+1 8 e para todo n ∈ N∗ . As > a1 > 0 < e 0<q<1 condi¸˜es para uma P.G. ser decrescente s˜o: co a > ou a1 < 0 e q>1 : Exemplo 3 1 1 1 a) (an ) = 1 , 2 , 4 , · · · temos que a1 = 1 ; q = 2 b) (an ) = − 2 , −4 , −8 , · · · temos que a1 = −2 ; q = 2 • (an ) ´ constante se a1 = 0 e q = 1. e Exemplo 4 (an ) = (2 , 2 , 2 , · · · ) • (an ) ´ singular se a1 = 0 ou q = 0. e Exemplo 5 a) (an ) = (0 , 0 , 0 , · · · ) temos que a1 = 0 ; q = qualquer b) (an ) = (3 , 0 , 0 , · · · ) temos que a1 = 3 ; q = 0 • (an ) ´ alternante se a1 = 0 e q < 0. e Exemplo 6 (an ) = (2 , −4 , 8 , −16 , · · · ) , a1 = 2 e q = −2. CEDERJ 116
- 119. Progress˜o Geom´trica a e ´ MODULO 1 - AULA 11 Termo Geral de uma P.G. Sabemos que, pela defini¸˜o, (an ) = (a , aq , aq 2 , · · · ). Da´ ca ı, an = a1 q n−1 . A express˜o acima ´ denominada termo geral de uma P.G. a e Exemplo 7 Em cada item abaixo, dada a P.G., determinemos sua raz˜o e sua classi- a fica¸˜o: ca 4 a) (an ) = (1 , 4 , 16 , 64 , · · · ), q = = 4, logo a P.G. ´ estritamente e 1 crescente. −9 1 b) (an ) = (−27 , −9 , −3 , · · · ), q = = , logo a P.G. ´ estritamente e −27 3 crescente. a1 = 18 a1 18 c) (an ) tal que an . Observe que a2 = = =6 an+1 = , ∀ n ∈ N∗ 3 3 3 a2 6 e a3 = = = 2. Da´ (an ) = (18 , 6 , 9 , · · · ). Ent˜o temos que ı, a 3 3 1 q = 3 , logo a P.G ´ estritamente decrescente. e −3 d) (an ) = (−1 , −3 , −9 , · · · ), q = = 3, logo, a P.G. ´ estritamente e −1 decrescente. −2 e) (an ) = (−2 , −2 , −2 , · · · ), q = = 1, logo a P.G. ´ constante. e −2 0 f) (an ) = (5 , 0 , 0 , · · · ), q = 5 = 0, logo a P.G ´ singular. e g) (an ) = (0 , 0 , 0 , · · · ), q ∈ R, logo a P.G ´ constante. e 3 h) (an ) = (−1 , 3 , −9 , 27 , · · · ), q = −1 = −3, logo a P.G. ´ alternante. e 117 CEDERJ
- 120. Progress˜o Geom´trica a e Exemplo 8 Se a1 , a2 , 1 , 1 , a5 , a6 , a7 formam, nessa ordem, uma P.G., achar a soma 4 2 desses termos. Solu¸˜o: ca Usando a defini¸˜o de P.G. temos: ca 1 1 1 4 q= ÷ = × = 2. 2 4 2 1 Da´ ı, 1 a5 = ×2=1 2 a6 = 1×2=2 a7 = 2 × 2 = 4 1 1 1 1 a2 = ÷2= × = 4 4 2 8 1 1 1 1 a1 = ÷2= × = . 8 8 2 16 Portanto, 1 1 1 1 127 S= + + + +1+2+4= . 16 8 4 2 16 Exerc´ ıcios Propostos 1. A sequˆncia (an ) = (1 , a , · · · ) ´ uma P.G. O nono termo dessa pro- e e gress˜o ´ 256. Ent˜o, o valor de a pode ser: a e a 1 a) 4 b) 3 c) 2 d) 2 e) 8 2. Se o 7o termo de uma P.G. ´ − 1 e o 14o termo ´ -729, ent˜o o 10o termo e 3 e a ´: e a) -27 b) -18 c) -54 d) -9 e) -36 3. Numa P.G. a diferen¸a entre o 2o e o 1o termo ´ 9 e a diferen¸a entre c e c o 5o e o 4o termo ´ 576. Ent˜o o 1o termo dessa progress˜o ´: e a a e a) 3 b) 4 c) 6 d) 8 e) 9 4. Em um parque ecol´gico, h´ cinco anos, a popula¸˜o de on¸as pintadas o a ca c era de 325. Hoje ela ´ de 481. Ent˜o a taxa m´dia anual de crescimento e a e da popula¸˜o de on¸as, se elas s´ se reproduzem uma vez por ano ´ de: ca c o e 1 (Dado: 1, 48 5 = 1, 082) a) 6,7% b) 5,8% c) 7,6% d) 8,2% e) 8,5% CEDERJ 118
- 121. Progress˜o Geom´trica a e ´ MODULO 1 - AULA 11 5. Um pa´ contraiu em 1829 um empr´stimo de 1 milh˜o de d´lares para ıs e a o pagar em cem anos a taxa de juros de 9% ao ano. Por problemas de balan¸a comercial, nada foi pago at´ hoje e a d´ c e ıvida foi sendo “rolada” com capitaliza¸˜o anual de juros. Qual dos valores abaixo est´ mais ca a pr´ximo do valor da d´ o ıvida em 1989? a) 14 bilh˜es de d´lares o o b) 500 bilh˜es de d´lares o o c) 700 bilh˜es de d´lares o o d) 4 bilh˜es de d´lares o o e) 4 trilh˜es de d´lares o o 6. Numa P.G. de quatro termos positivos, a soma dos dois primeiros vale 1 e a soma dos dois ultimos vale 9. Calcule a raz˜o dessa progress˜o. ´ a a 7. Sabendo-se que uma c´lula se divide em duas a cada segundo, qual o e total de c´lulas ao final de 10 segundos? e 8. Se S3 = 21 e S4 = 45 s˜o, respectivamente, as somas dos trˆs e quatro a e primeiros termos de uma P.G. cujo termo inicial ´ 3, ent˜o a soma dos e a cinco primeiros termos dessa progress˜o ´: a e a) 66 b) 69 c) 93 d) 96 e) 105 Propriedades de uma P.G. Propriedade 1 (Termos Equidistantes) O produto de dois termos equidistantes dos extremos ´ igual ao produto dos e extremos, ou seja, se p + k = n + 1 temos ap · ak = a1 · an . De fato, suponhamos p + k = n + 1. Ent˜o, sejam a ap = a1 · q p−1 ak = a1 · q k−1 an = a1 · q n−1 Fazendo ap · ak temos: ap · ak = a1 · a1 · q p+k−2 = a1 · a1 · q n+1−2 = a1 · a1 · q n−1 = a1 · an . Exemplo 9 Seja (an ) = (1 , 2 , 4 , 8 , 16 , 32). Note que: 1 × 32 = 2 × 16 = 4 × 8 . 119 CEDERJ
- 122. Progress˜o Geom´trica a e Propriedade 2 (M´dia Geom´trica) e e Cada termo de uma P.G., a partir do segundo, ´ a m´dia geom´trica entre o e e e termo anterior e o posterior. Seja (an ) = (a1 , a2 , · · · , ap−1 , ap , ap+1 , · · · ). Vamos provar que a2 p = ap−1 · ap+1 . De fato, sejam ap−1 = a1 · q p−1−1 ap+1 = a1 · q p+1−1 ap = a1 · q p−1 Fazendo ap−1 · ap+1 temos: ap−1 · ap+1 = a1 · a1 · q 2p−2 = a1 · q p−1 · a1 · q p−1 = a2 . p Logo, a2 = ap−1 · ap+1 . p Exemplo 10 Seja (an ) = (3 , 9 , 27 , 81 , 243 , · · · ). Note que: 92 = 3 × 27 272 = 9 × 81 812 = 27 × 243 Exemplo 11 O terceiro e o s´timo termo de uma P.G. valem, respectivamente, 10 e 18. e Determine o quinto termo dessa progress˜o. a Solu¸˜o: ca Note que 5 + 5 = 3 + 7. Logo, a5 · a5 = a3 · a7 (propriedade 1) a2 = 10 × 18 5 √ a2 = 180 =⇒ a5 = 6 5 5 √ Logo, o quinto termo dessa progress˜o vale 6 5. a CEDERJ 120
- 123. Progress˜o Geom´trica a e ´ MODULO 1 - AULA 11 Exerc´ ıcios Propostos √ 9. A sequˆncia de n´ meros reais e positivos dado por x − 2 , e u x2 + 11 , 2x + 2 , · · · ´ uma P.G. cujo s´timo termo vale: e e a) 96 b) 192 c) 484 d) 252 e) 384 10. Numa P.A. de termos positivos, o 1o , o 5o e o 21o termo formam, nessa ordem, uma P.G. A raz˜o dessa P.G. ´: a e a) 2 b) 4 c) 16 d) 20 e) imposs´ de ser determinado ıvel 11. Se (A1 , A2 , A3 , · · · ) ´ uma P.G de termos positivos e distintos e de e raz˜o q, ent˜o (log A1 , log A2 , log A3 , · · · ) a a a) ´ uma P.G. de raz˜o q e a d) ´ uma P.A. de raz˜o log q e a b) ´ uma P.G. de raz˜o log q e a e) n˜o ´ P.A. nem P.G. a e c) ´ uma P.A. de raz˜o log q 2 e a 12. Numa P.G. estritamente decrescente, sabe-se que a1 + a10 = −513 e a4 · a7 = 512. Determine a raz˜o dessa P.G. a 13. Adicionando-se a mesma constante a cada um dos n´ meros 6, 10 e 15, u nessa ordem, obtemos uma P.G. de razˆo: a 5 3 5 a) 4 b) 2 c) 3 d) 4 e) 31 Produto de n Termos de uma P.G. Teorema 1 Se (an ) ´ uma P.G e Pn ´ produto dos n primeiros termos, ent˜o e e a |Pn | = (a1 · an )n . Demonstra¸˜o: ca De fato, sejam Pn = a1 · a2 · . . . · an Pn = an · an−1 · . . . · a1 Pn = (a1 · an )(a2 · an−1 ) · · · (an · a1 ) = (a1 · an )n 2 (propriedade 1) . Da´ ı, |Pn | = (a1 · an )n . 121 CEDERJ
- 124. Progress˜o Geom´trica a e Obs.: A f´rmula anterior nos permite calcular o m´dulo do produto. Para o o obter o sinal de Pn , basta analisar o sinal dos termos. Exemplo 12 Na P.G. (1 , −3 , 9 , −27 , · · · ), determine o produto dos 8 primeiros termos. Solu¸˜o: ca Observe que −3 q = = −3 1 a8 = a1 q 7 = 1 × (−3)7 = (−1) × 37 . Da´ ı, √ |P8 | = (a1 · a8 )8 = (1 × (−1) × 37 )8 = 356 = 328 . Como dos 8 termos 4 s˜o positivos e 4 s˜o negativos, temos que a a P8 = 328 . Soma dos n Primeiros Termos de uma P.G. Teorema 2 Se (an ) ´ uma P.G. de raz˜o q e Sn a soma dos n primeiros termos de (an ) e a ent˜o: a Sn = n · a1 se q = 1 a1 1 − q n a1 q n − 1 Sn = = se q = 1 1−q q−1 Demonstra¸˜o: ca De fato, se q = 1 ent˜o Sn = n · a1 . Vamos considerar o caso q = 1. a Sn = a1 + a2 + · · · + an−1 + an Sn q = a1 q + a2 q + · · · + an−1 q + an q Sn q − Sn = an · q − a1 Sn (q − 1) = a1 q n−1 · q − a1 = a1 q n − a1 a1 q n − 1 Sn = . q−1 CEDERJ 122
- 125. Progress˜o Geom´trica a e ´ MODULO 1 - AULA 11 Exemplo 13 Determine a soma dos 10 primeiros termos da P.G. (1 , 3 , 9 , 27 , · · · ). Solu¸˜o: ca 3 Temos que q = 1 = 3. Ent˜o: a a1 q 10 − 1 1 × 310 − 1 310 − 1 S10 = = = = 29524 . q−1 3−1 2 Exerc´ ıcios Propostos 14. Numa P.G estritamente decrescente tem-se a1 = − 1 e a15 = −9. O 9 produto dos 15 primeiros termos ´: e a) 1 b) -1 c) 11 d) -11 e) 215 √ 15. Uma P.G tem primeiro termo igual a 1 e raz˜o igual a 2 . Se o produto a dos termos dessa progress˜o ´ 239 , ent˜o o n´ mero de termos ´ igual a: a e a u e a) 12 b) 13 c) 14 d) 15 e) 16 16. Uma P.G. de 8 termos tem primeiro termo igual a 10. O logaritmo decimal do produto de seus termos vale 36. Ache a raz˜o dessa pro- a gress˜o. a 17. Dada a P.G. finita (5 , 50 , · · · , 5000000), sua soma resulta: a) 5.555.555 b) 10.000.000 c) 9.945.555 d) 55.555.555 e) infinita 18. A soma dos cinco primeiros termos de uma P.G., sabendo-se que o quinto termo ´ 162 e a raz˜o ´ igual a 3 ´: e a e e a) 162 b) 620 c) 324 d) 242 e) 342 19. O n´ mero de ancestrais de uma pessoa, em seis gera¸˜es ´: u co e a) 63 b) 126 c) 127 d) 32 e) 64 Limite da Soma O Limite da Soma dos Infinitos Termos de uma P.G. Teorema 3 Seja (an ) uma P.G. de raz˜o q tal que −1 < q < 1. A soma S dos infinitos a a1 termos dessa P.G. existe, ´ finita e igual a lim S = e . n→∞ 1−q 123 CEDERJ
- 126. Progress˜o Geom´trica a e Demonstra¸˜o: ca De fato, como −1 < q < 1 ent˜o: a lim q n = 0 . n→∞ (N˜o provaremos este resultado aqui pois foge ao nosso objetivo). Logo, a a1 1 − q n a1 (1 − 0) S = a1 + a2 + · · · + an−1 + an + an+1 · · · = lim Sn = lim = . n→∞ n→∞ 1−q 1−q Portanto: a1 S= . 1−q Exemplo 14 1 1 1 Determine a soma dos infinitos termos da P.G. 1 , 2 , 4 , 8 , ··· . Solu¸˜o: ca 1 1 Como q = 2 = , temos que −1 < q < 1 e podemos aplicar a equa¸˜o ca 1 2 a1 S = 1−q para calcularmos essa soma. Logo: a1 1 1 S= = 1 = 1 = 2. 1−q 1− 2 2 Exerc´ ıcios Propostos 20. A soma 1 − 3 + 4 − 2 9 8 27 + · · · vale: 2 3 4 a) 5 b) 5 c) 5 d) 1 e) 3 21. Seja Sn a soma dos n primeiros termos da sequˆncia infinita 10−1 , 10−2 , e 10−3 , · · · , 10−n , · · · . a) Calcule S5 b) Qual o limite de Sn quando n tende a ∞? 22. Roberto chega `s 15 h para um encontro que havia marcado com a Rosˆngela. Como Rosˆngela n˜o chegara ainda, Roberto resolveu es- a a a perar um tempo t1 igual a meia hora e ap´s isso, um tempo t2 = 1 · t1 o 2 1 e ap´s isso, um tempo t3 = 2 · t2 e assim por diante. Se Rosˆngela n˜o o a a foi ao encontro, quanto tempo Roberto esperou at´ ir embora? e a) 45 min b) 50 min c) 55 min d) 1 h e) 2 h √ 23. O valor de 0, 4 + 0, 04 + 0, 004 + · · · ´: e a) 0,222. . . b) 0,333. . . c) 0,444. . . d) 0,555. . . e) 0,666. . . CEDERJ 124
- 127. Progress˜o Geom´trica a e ´ MODULO 1 - AULA 11 24. Na figura a seguir A1 B1 = 3 , B1 A2 = 2. Calcule a soma dos infinitos segmentos A1 B1 + B1 A2 + A2 B2 + B2 A3 + · · · A1 A2 A3 B2 B1 25. Uma bola ´ lan¸ada na vertical, de encontro ao solo, de uma e c altura h. Cada vez que bate no solo, ela sobe at´ a metade da e altura que caiu. Calcular o comprimento total percorrido pela mesma bola em suas trajet´rias at´ atingir o repouso. o e √ 26. O valor de x x x x · · · ´: e 2 1 a) x b) 2x c) x2 d) x e) x 3 357 357 357 27. O limite da soma dos termos da P.G. 103 , 106 , 109 , · · · ´: e 357 a) 357 b) 99 c) 357,357357. . . d) 0,357357357. . . e) 0,357 Exerc´ ıcios Complementares 28. Quantos termos da P.G. (1 , 3 , 9 , · · · ) devem ser somados para que a soma seja 3.280? a) 4 b) 6 c) 8 d) 10 e) 12 √ 1 1 2 29. O limite da soma dos termos da P.G. √ 2 , 2 , 4 , ··· ´: e √ √ √ √ √ a) 32 b) 2 + 1 c) 2 − 1 d) 2 +1 3 e) 1− 2 2 √ √ 3 30. Os trˆs primeiros termos de uma P.G. s˜o a1 = e a 2 , a2 = 2 e √ 6 o a3 = 2. O 4 termo ´: e 1 √ √ 1 a) √2 b) 1 c) 5 2 d) 3 2 e) 2 125 CEDERJ
- 128. Progress˜o Geom´trica a e x2 x2 x2 31. Os valores de x de modo que x2 − 9 + 4 − 8 + · · · = 6 s˜o: a a) -3 e 5 b) -5 e 3 c) 3 e -3 d) 5 e -5 e) 0 e 2 32. A soma dos trˆs n´ meros que formam uma P.A. crescente ´ 36 e se e u e somarmos 6 unidades ao ultimo, eles passam a constituir uma P.G. de ´ raz˜o: a 1 1 a) 2 b) 3 c) 2 d) -3 e) 4 33. O n´ mero real x ´ positivo e diferente de 1. O quadrado de x, o u e pr´prio x e log x formam uma P.G., nessa ordem. Ent˜o x vale: o a 1 a) -1 b) 0 c) 10 d) 1 e) 10 √ √ 34. Dada a P.G. · · · , 1 , 32−1 , 2− 3 2 , · · · o termo que precede 1 ´: e √ √ √ √ √ a) 1 − 3 b) 3 + 1 c) 1+2 3 d) 3 − 1 e) 1−2 3 35. Os ˆngulos de um triˆngulo est˜o em P.G. de raz˜o 2. Ent˜o o triˆngulo: a a a a a a a) tem um ˆngulo de 60o a b) ´ retˆngulo e a c) ´ acutˆngulo e a d) ´ obtusˆngulo e a e) ´ is´sceles e o 36. A sequˆncia (x , xy , 2x), com x = 0 ´ uma P.G. Ent˜o: e e a a) x ´ um n´ mero racional e u b) x ´ um n´ mero irracional e u c) y ´ um n´ mero racional e u d) y ´ um n´ mero irracional e u y e) x ´ um n´ mero irracional e u 37. Em uma P.G. em que a8 = 10 e a15 = 1280, a raz˜o ´ igual a: a e 1 a) 2 b) 4 c) -2 d) 2 e) 3 CEDERJ 126
- 129. Progress˜o Geom´trica a e ´ MODULO 1 - AULA 11 Gabarito dos Exerc´ ıcios Propostos 1. c 10. b 19. b 2. d 11. d 20. b 3. a 12. 2 21. a) 0, 11111 1 4. d 13. a b) 9 5. e 14. b 22. d 6. q=3 15. b 23. e 7. 1024 16. q = 10 ou q = −10 24. 9 8. c 17. a 25. 3 h 9. b 18. d 26. d 27. d Gabarito dos Exerc´ ıcios Complementares 28. c 29. b 30. b 31. c 32. c 33. e 34. b 35. d 36. d 37. a 127 CEDERJ
- 131. Conjuntos ´ MODULO 1 - AULA 12 Aula 12 – Conjuntos Objetivos: Nesta aula pretendemos que vocˆ: e • Entenda o conceito de conjunto e possa realizar opera¸˜es entre con- co juntos. • Recorde a estrutura dos conjuntos num´ricos. e • Trabalhe com intervalos de n´ meros reais e realize opera¸˜es entre in- u co tervalos. Introdu¸˜o ca Conjunto ´ toda reuni˜o de elementos (pessoas, objetos, n´ meros, etc.) e a u que podem ser agrupadas por possu´ ırem caracter´ısticas comuns. Exemplo: o conjunto de todas as letras de nosso alfabeto ou o conjunto de todas as mulheres brasileiras. S´ ımbolos Para representar conjuntos usamos as letras mai´ sculas A, B, C . . . e u para representar elementos de conjuntos usamos letras min´sculas a, b, c, d . . . u Exemplo: A = {a, e, i, o, u} tamb´m pode ser escrito como A = {x | x ´ e e vogal de nosso alfabeto}. Para representar que u est´ no conjunto A e que a o elemento d n˜o est´ no conjunto A escrevemos u ∈ A “lˆ-se u pertence a a a e A” e d ∈ A “lˆ-se d n˜o pertence a A”. / e a Conjunto unit´rio e conjunto vazio a Um conjunto que possui apenas um elemento ´ dito um conjunto unit´rio. e a Um conjunto que n˜o possui elemento ´ um conjunto vazio. Usamos o s´ a e ımbolo ∅ para representar um conjunto vazio. Exemplo: Se B = {x | os dias da semana cuja primeira letra ´ f } ent˜o B = ∅. e a Subconjuntos Um conjunto B cujos elementos todos pertencem a um outro conjunto A ´ dito um subconjunto deste outro conjunto. e 129 CEDERJ
- 132. Conjuntos Exemplo: A = {a, b, c, d, e, f }, B = {a, e} e C = {a, e, i} ent˜o B ´ um a e subconjunto de A, C n˜o ´ um subconjunto de A. Usamos a nota¸˜o: a e ca B ⊂ A “lˆ-se B est´ contido em A” ou A ⊃ B “lˆ-se A cont´m B” e C ⊂ A e a e e “lˆ-se C n˜o est´ contido em A”. e a a Uni˜o, interse¸˜o e produto cartesiano de conjuntos a ca Dados dois conjuntos A e B podemos formar trˆs novos conjuntos: e i) o conjunto uni˜o de A e B ´ o conjunto formado por todos os elementos a e de A e de B, A ∪ B {x | x ∈ A ou x ∈ B} “lˆ-se o conjunto dos x e tal que se x pertence a A ou x pertence a B” A B ii) o conjunto interse¸˜o de A e B ´ o conjunto dos elementos que est˜o ca e a simultaneamente em A e em B. A∩B = {x | x ∈ A e x ∈ B} “lˆ-se o conjunto dos x tal que x pertence e a A e x pertence a B”. A B Exemplo: Se B = {a, e, i} e A = {a, b, c, d, e} ent˜o a A ∪ B = {a, b, c, d, e, i} e A ∩ B = {a, e}. iii) o conjunto produto cartesiano, A × B, de A por B ´ um novo conjunto, e definido por A × B = {(x, y) | x ∈ A e y ∈ B} . Exemplo: Se A = {1, 2} e B = {a, b}, ent˜o a A × B = {(1, a), (1, b), (2, a), (2, b)} . Nota: Se A tem n elementos e B tem m elementos ent˜o A × B tem m · n a elementos. CEDERJ 130
- 133. Conjuntos ´ MODULO 1 - AULA 12 Conjunto Diferen¸a e Conjunto Complementar c O conjunto diferen¸a entre os conjuntos A e B ´ formado pelos elemen- c e tos que pertencem a A e n˜o pertencem a B. Usamos a nota¸˜o A − B para a ca o conjunto diferen¸a. c A − B = {x | x ∈ A e x ∈ B}. / A B Quando estamos estudando conjuntos, podemos nos referir ao conjunto universo representado pela letra U. Numa situa¸˜o especificada U ´ o con- ca e junto que cont´m como subconjuntos os conjuntos estudados. e A ⊂ U “lˆ-se o conjunto A est´ contido no conjunto universo U”. e a U A O conjunto complementar do conjunto A ´ o conjunto formado pelos ele- e mentos do conjunto universo que n˜o pertence a A. Ent˜o na verdade este a a conjunto ´ igual a U − A. e Tamb´m ´ comum o uso da nota¸˜o Ac . Assim, Ac = {x | x ∈ U e x ∈ A}. e e ca / Tamb´m aparece a nota¸˜o CA e A. e ca Exemplo: A = {1, 3, {2, 4}, a, b}. O conjunto A possui 5 elementos. Podemos escrever que 3 ∈ A e que {2, 4} ∈ A. Note que n˜o ´ correto escrever a e {2, 4} ⊂ A. No entanto ´ perfeito escrever: {{2, 4}} ⊂ A. e Caso Particular Quando temos dois conjuntos A e B, tais que B ⊂ A, a diferen¸a A − B ´ c e chamada de Complemento de B em rela¸˜o a A, representado por CA B. ca A B CA B ´ o que falta a B para ser igual a A. e Por exemplo, se A = {a, e, i} e B = {a}, ent˜o: a CA B = A − B = {e, i}. Observa¸˜o: Sendo U o conjunto Universo, ent˜o escrevemos: ca a U − A = CU A = CA = A. 131 CEDERJ
- 134. Conjuntos Conjunto das partes Dado um conjunto A definimos o conjunto das partes de A, P (A), como o conjunto cujos elementos s˜o todos os subconjuntos de A. a P (A) = {X | X ´ subconjunto de , A}. e Exemplo: Se A = {a, e, i, } ent˜o P (A) = {∅, {a}, {e}, {i}, {a, e}, {a, i}, {e, i}, {a, e, i}}. a Nota: Se um conjunto tem n elementos ent˜o P (A) possui 2n elementos. a N´mero de elementos de um conjunto u Um conjunto ´ dito finito quando possui um n´ mero finito n de elemen- e u tos. Em caso contr´rio o conjunto ´ chamado infinito. Dados os conjuntos a e finitos A e B representamos por n(A) o n´ mero de elementos de A; por n(B) u o n´ mero de elementos de B; por n(A ∪ B) o n´ mero de elementos de A ∪ B u u e por n(A ∩ B) o n´ mero de elementos de A ∩ B. N˜o ´ dif´ provar que u a e ıcil n(A ∪ B) = n(A) + n(B) − n(A ∩ B). Veja por quˆ. Qual ´ o m´todo para encontrar n(A ∪ B), o n´ mero e e e u de elementos do conjunto A ∪ B. Contamos A e B e somamos, obtendo n(A) + n(B). Agora fa¸o a seguite pergunta: em que circunstˆncia ´ correto c a e escrever n(A ∪ B) = n(A) + n(B) ? A resposta ´: apenas quando A ∩ B = ∅. Pois nessa situa¸˜o, contar e ca A ∪ B ´ equivalente a contar A, contar B e adicionar os resultados. No caso e em que A ∩ B = ∅, ao escrevermos n(A) + n(B), estaremos contando duas vezes os elementos de A ∩ B ⊂ A ∪ B. Portanto, de modo geral, vale n(A ∪ B) = n(A) + n(B) − n(A ∪ B). Em seguida, recordamos e listamos algumas propriedades e observa¸˜es in- co teressantes. ımbolo ∈ ´ usado para relacionar um elemento e seu conjunto en- a) o s´ e ımbolo ⊂ ´ usado para relacionar dois conjuntos. quanto que o s´ e b) O conjunto vazio ´ subconjunto de qualquer conjunto. ∅ ⊂ A, para e qualquer conjunto A. c) A ⊂ A, todo conjunto est´ contido em si pr´prio. a o d) Tamb´m A ∈ P (A) e ∅ ∈ P (A). e e) A ⊂ U. Todo conjunto ´ subconjunto de um conjunto universo. e f) Se A ⊂ B e B ⊂ C ent˜o A ⊂ C. a g) Se A ⊂ B e B ⊂ A ent˜o B = A (esta ´ uma maneira muito util de a e ´ verificar que dois conjuntos s˜o iguais). a CEDERJ 132
- 135. Conjuntos ´ MODULO 1 - AULA 12 Representa¸˜o de Conjuntos Num´ricos ca e Podemos representar geometricamente os n´ meros reais em uma reta. u A cada ponto da reta est´ associado um n´ mero real e a cada n´mero real a u u est´ associado um ponto da reta. a B O I A IR -1 0 1 2 2 3 Para fazer a representa¸˜o escolhemos dois pontos O e I da reta e ca associamos a eles os n´ meros reais 0 e 1, respectivamente. O segmento de u reta OI ´ muito especial. Foi escolhido para ter comprimento 1. Veja a e Figura acima. Os n´ meros reais negativos s˜o colocados na reta ` esquerda u a a do ponto O e os n´ meros positivos ` direita do ponto zero. u a Nesta representa¸˜o, a distˆncia entre os n´ meros inteiros n e n + 1 ´ ca a u e a mesma distˆncia que entre os n´ meros 0 e 1. a u √ Tamb´m, por exemplo, 2 e −π ganharam as posi¸˜es indicadas na e co figura acima, em fun¸˜o de que os segmentos de reta OA e OB medem ca √ respectivamente, 2 e π. Na continua¸˜o de nosso estudo vamos usar (na verdade, j´ estamos ca a usando) os seguintes s´ ımbolos: | significa “tal que” ∃ significa “existe” ∧ significa “e” ∨ significa “ou” ⇔ significa “equivalente” ⇒ significa “implica que” (i) Intervalos de n´ meros reais. u Intervalos s˜o subconjuntos dos n´ meros reais determindos por desigualda- a u des. Sendo a ∈ R, b ∈ R e a < b, temos: Intervalo fechado {x ∈ R | a ≤ x ≤ b} = [a, b]. Lˆ-se: x pertence a R, tal que x seja igual e ou maior que a e igual ou menor que b. [a, b] ´ o conjunto dos n´ meros reais e u compreendidos entre a e b, incluindo a e b. Representamos na reta [a, b] por: a b 133 CEDERJ
- 136. Conjuntos Exemplo: [5, 8] = {x ∈ R | 5 ≤ x ≤ 8}. x pode ser igual ou maior que 5 e igual ou menor que 8. 5 8 Note que na figura acima os pontos a e b s˜o representados por um ponto a ´ uma conven¸˜o que adotamos para significar que a e b pertencem cheio. E ca ao intervalo [a, b]. Intervalo aberto {x ∈ R | a < x < b} = (a, b) ´ o conjunto dos n´ meros reais compreendidos entre a e b, n˜o incluindo a e e u a b. Veja a representa¸˜o geom´trica abaixo. ca e a b Note que na figura acima os pontos a e b s˜o representados por pon- a ´ tos vazados. E uma conven¸˜o para significar que a e b n˜o pertencem ao ca a intervalo (a, b). Exemplo: (5, 8) = {x ∈ R | 5 < x < 8} ´ o conjunto dos n´ meros maiores e u que 5 e menores que 8. 5 8 Intervalo aberto ` esquerda e fechado ` direita a a {x ∈ R | a < x ≤ b} = (a, b] ´ o conjunto dos n´ meros reais compreendidos entre a e b, n˜o incluindo a e e u a incluindo b. Veja a representa¸˜o geom´trica abaixo. ca e a b Exemplo: (5, 8] = {x ∈ R | 5 < x ≤ 8} ´ o conjunto formado pelos n´ meros e u maiores que 5 e iguais ou menores que 8. Intervalo fechado ` esquerda e aberto ` direita a a {x ∈ R | a ≤ x < b} = [a, b) ´ o conjunto dos n´ meros reais compreendidos entre a e b incluindo a e n˜o e u a incluindo b. Veja a interpreta¸˜o geom´trica abaixo. ca e a b CEDERJ 134
- 137. Conjuntos ´ MODULO 1 - AULA 12 Exemplo: [5, 8) = {x ∈ R | 5 ≤ x < 8} ´ o conjunto dos n´ meros maiores que e u 5 ou iguais a 5 e menores que 8 5 8 Intervalos infinitos [a, ∞) = {x ∈ R | x ≥ a}, ´ o conjunto de todos os n´ meros reais maiores ou iguais ao n´ mero a. Veja e u u a representa¸˜o geom´trica abaixo. ca e a Exemplo: (2, ∞) = {x ∈ R | x > 2} 2 Outro exemplo:(−∞, −1)={x ∈ R | x < −1}. -1 0 Nota: R = (−∞, ∞). Potˆncias e ra´ e ızes de n´meros reais u Dado um n´ mero real b e um n´ mero natural n ≥ 1, ao produto de n u u fatores b, denominamos potˆncia n-´sima de b e representamos por bn . Isto e e ´, e bn = b.b.b...b (n fatores) Tamb´m se b = 0 e m ´ um n´ mero inteiro negativo ent˜o a m-´sima potˆncia e e u a e e de b, ´ definido por e 1 −m 1 1 1 bm = = . ... (−m fatores) b b b b Por defini¸˜o, se b = 0, colocamos, ca b0 = 1. Note que, das defini¸˜es anteriores, vem que se n e m s˜o n´ meros inteiros, co a u b = 0 e c = 0, ent˜o, a m 1 −m b m bm a) b = b) = m b c c c) (b.c)n = bn .cn d) bm .bn = bm+n e) (bm )n = bm.n 1 3 1 1 Exemplos: = 3 = 2 2 8 2 −3 3 3 (−3)3 27 − = − = 3 =− 3 2 2 8 135 CEDERJ
- 138. Conjuntos Ra´ ızes de n´ meros reais u Considere um n´ mero natural n e um n´ mero real b. Queremos encon- u u trar um outro n´ mero real x tal que u xn = b. Caso x exista, chamamos este n´ mero de raiz n-´sima de b e indicamos como u e √ n x= b. Casos de existˆncia da raiz e √ n √ 4 1) Se n > 0 ´ par e b ≥ 0 ent˜o sempre existe e a b. Por exemplo, 81 = 3. √ No entanto n˜o tem sentido −2. a 6 √ n 2) Se n > 0 ´ ´ e ımpar e b ´ um n´ mero real qualquer ent˜o existe e u a b. Por exem- plo, √ 1 1 3 −125 = −5, 5 − =− . 243 3 √ Nota 1: No caso de 2 b, onde b ´ um n´ mero real positivo, indicamos sim- e u √ √ plesmente por b e lemos “raiz quadrada de b”. Tamb´m 3 c, onde c ´ um e e n´ mero real, lemos “raiz c´ bica de c”. u u Nota 2: Sempre que a raiz estiver bem definida vale √ √n √ √ n a n a a .b = a . b e n n = √ . b n b Potˆncia racional de um n´mero real e u m Se b ´ um n´ mero real e q = e u ´ um n´ mero racional, onde n > 0, e u n ent˜o definimos a m √ bq = b n = bm , n desde que a raiz n-´sima de bm esteja bem definida. e Exemplo: 2 1 1 1 1 (−9)− 3 = 3 (−9)−2 = 3 = 3 = √ = √ . (−9)2 81 3 81 333 CEDERJ 136
- 139. Conjuntos ´ MODULO 1 - AULA 12 Exerc´ ıcios 1. Dado o conjunto A = {x, y, z}, associar V (verdadeira) ou F (falsa) em cada senten¸a a seguir: c a) 0 ∈ A b) y ∈ A / c) A = {y, x, z} d) x ∈ A e) {x} ∈ A f) A ∈ A 2. Sendo A = {2, 3, 5} e B = {0, 1}, escrever em s´ ımbolos da teoria dos conjuntos: a) 2 pertence a A b) 1 pertence a B c) 3 n˜o pertence a B a d) A n˜o ´ igual a B a e 3. Sendo A = {0, 2, 4, 6, 8, 10}, B = {2, 6, 8}, C = {0, 2, 3, 4, } e D = {0, 2, 6, 8}, assinalar as afirma¸˜es verdadeiras: co a) B ⊂ A, b) B ⊂ D c) C ⊂ D, d) D ⊂ A e) A ⊃ C, f) A ⊃ B g) D ⊃ B, h) C ⊂ A 4. (FGV-72) Se A = {1, 2, 3, {1}} e B = {1, 2, {3}}, (A − B) ´: e a) {3, {2}}, b) {3, {1}}, c) {0, {+2}} d) {0, {0}} 5. (EPUSP-70) No diagrama, a parte hachurada representa: a) (A ∪ C) − B b) (B ∩ C) − A B A c) (A ∩ B) − C d) (A ∩ C) ∪ B e) A − (B − C) C 6. (AMAN-74) Dados os conjuntos A = ∅ e B = ∅ tais que (A ∪ B) ⊂ A ent˜o: a a) A ⊂ B b) A ∩ B = ∅ c) A ∪ B = ∅ d) B ⊂ A e) B ∈ A 137 CEDERJ
- 140. Conjuntos 7. (CONCITEC-72) Seja A um conjunto de 11 elementos. O conjunto Y de todos os subconjuntos de A tem n elementos. Pode-se concluir que: a) n = 2.048 b) n = 2.047 c) n = 2.049 d) n = 2.046 e) 2.050 8. (MACK-SP-79) Se A e B s˜o dois conjuntos tais que A ⊂ B e A = ∅, a ent˜o a a) sempre existe x ∈ A tal que x ∈ B. / b) sempre exite x ∈ B tal que x ∈ A. / c) se x ∈ B ent˜o x ∈ A. a d) se x ∈ B ent˜o x ∈ A. / a / e) A ∩ B = ∅ 9. (CESGRANRIO-79) O n´ mero de conjuntos X que satisfazem: {1, 2} ⊂ u X ⊂ {1, 2, 3, 4} ´: e a) 3 b) 4 c) 9 d) 6 e) 7 10. (PUC-RJ-79) O n´ mero de elementos do conjunto A ´ 2m e o n´ mero u e u n de elementos do conjunto B ´ 2 . O n´ mero de elementos de (A × B) e u ´: e a) 2m + 2n b) 2m×n c) 2m+n d) m × n e) m + n 11. (FGV-SP-80) Considere as afirma¸˜es a respeito da parte hachurada co do diagrama seguinte: OBS.: U = A ∪ B ∪ C ´ o conjunto universo e B e C s˜o os comple- e a mentares de B e C, respectivamente. I) A ∩ (B ∪ C) B A II) A ∩ (B ∩ C) III) A ∩ (B ∩ C) IV) A ∩ (B ∩ C) C A(s) afirma¸˜o(¸˜es) correta(s) ´ (s˜o): ca co e a a) I b) III c) I e IV d) II e III e) II e IV 12. (UFRS-80) Sendo A = {0, 1} e B = {2, 3}, o n´ mero de elementos u [P (A) ∩ P (B)] ´: e a) 0 b) 1 c) 2 d) 4 e) 8 CEDERJ 138
- 141. Conjuntos ´ MODULO 1 - AULA 12 13. Dados A = [1, ∞), B = (−∞, −2) ∪ (1, ∞) e C = [−3, 4], assinale falso ou verdadeiro ( ) A−B =∅ ( ) (A ∪ B) ∩ C = [1, 4] ( ) CR B = [−2, 1] ( ) A ∩ B ∩ C = (1, 4] 14. (ITA) Depois de N dias de f´rias, um estudante observa que: e I - Choveu 7 vezes, de manh˜ ou ` tarde. a a II - Quando chove de manh˜, n˜o chove ` tarde. a a a III - Houve 5 tardes sem chuva. IV - Houve 6 manh˜s sem chuva. a O n´ mero N de dias de f´rias foi: u e a) 7 b) 9 c) 10 d) 11 e) 8 Gabarito 1. a) F , b) F , c) V , d) V , e) F , f) F . 2. a) 2 ∈ A, b) 1 ∈ B, c) 3 ⊂ B, d) A = B. 3. a), c), d), g), h) s˜o verdadeiras. 4. b) 5. c) 6. d) 7. a) a 8. d) 9. b) 10. c) 11. d) 12. b) 13. F, V, V, V 14 b) 139 CEDERJ
- 143. Introdu¸˜o `s fun¸oes ca a c˜ ´ MODULO 1 - AULA 13 Aula 13 – Introdu¸˜o `s fun¸˜es ca a co Objetivos: Ap´s estudar esta aula vocˆ ser´ capaz de: o e a • Distinguir entre uma rela¸˜o e uma fun¸˜o entre dois conjuntos. ca ca • Definir dom´ ınio, contradom´ ınio e esbo¸ar gr´ficos de fun¸˜es. c a co Produto cartesiano Dados dois conjuntos n˜o vazios A e B, o produto cartesiano de A por a B ´ o conjunto formado pelos pares ordenados, nos quais o primeiro elemento e pertence a A e o segundo elemento pertence a B. A × B = {(x, y) | x ∈ A e y ∈ B}. Exemplo: Se A = {1, 2} e B = {a, b, c}, ent˜o: a A × B = {(1, a); (1, b); (1, c); (2, a); (2, b); (2, c)} e B × A = {(a, 1); (a, 2); (b, 1); (b, 2); (c, 1); (c, 2)} Notas: 1) De modo geral A × B = B × A. 2) Se A = ∅ ou B = ∅, por defini¸˜o A × B = ∅, isto ´, A × ∅ = ∅ ou ca e ∅ × B = ∅. 3) Se A = B podemos escrever o produto cartesiano A × A como A2 , isto ´, A × A = A2 . e 4) O produto cartesiano de duas c´pias do conjunto de n´ meros reais R, o u fornece R2 = {(x, y) | x ∈ R e y ∈ R}. Como vimos na Aula 1, os n´ meros reais podem ser identificados com u 2 uma reta. Tamb´m R , pode ser identificado com um plano, atrav´s de e e um sistema de coordenadas. Veja a figura abaixo, onde o ponto P do 141 CEDERJ
- 144. Introdu¸˜o `s fun¸oes ca a c˜ plano ´ identificado com um par de n´ meros reais: P = (x, y). Veja a e u 1 representa¸˜o do ponto Q = − 1, − . ca 2 5) Se os n´ meros de elementos dos conjuntos A e B s˜o n(A) e n(B) ent˜o u a a para o n´ mero de elementos de A × B vale n(A × B) = n(A) × n(B). u Rela¸˜es co Dados dois conjuntos A e B, uma rela¸˜o R sobre A e B (ou de A em ca B) ´ uma rela¸˜o que associa elementos x ∈ A a elementos y ∈ B, mediante e ca uma lei previamente determinada (lei de associa¸˜o ou de rela¸˜o). ca ca Como vocˆ ver´, atrav´s de exemplos, toda rela¸˜o de A em B deter- e a e ca mina um subconjunto de A × B. Exemplo: A = {−1, 0, 1, 3} B = {0, 1, 9, 10} Determine a) R1 = {(x, y) ∈ A × B | y = x2 } Solu¸˜o: ca R1 = {(−1, 1), (0, 0), (1, 1), (3, 9)} √ b) R2 = {(x, y) ∈ A × B | x = y} Solu¸˜o: ca R2 = {(1, 1), (3, 9), (0, 0)} Dom´ ınio e imagem ou contradom´ ınio Dada uma rela¸˜o R de A em B, chama-se dom´ ca ınio de R ao conjunto D de todos os elementos de A que aparecem como primeiros elementos nos pares ordenados de R. x ∈ D ⇔ ∃ y, y ∈ B | (x, y) ∈ R. CEDERJ 142
- 145. Introdu¸˜o `s fun¸oes ca a c˜ ´ MODULO 1 - AULA 13 Denominamos imagem da rela¸˜o R (ou contradom´ ca ınio) ao conjunto Im de todos os elementos de B que aparecem como segundos elementos nos pares ordenados de R. y ∈ Im ⇔ ∃ x, x ∈ A | (x, y) ∈ R. Exemplo: Sejam A = {0, 1, 2}, B = {−1, 1, 2, −2, 6} e R = {(0, −1), (0, 1), (2, 2), (2, −2)}. Ent˜o a D = {0, 2) e Im = {−1, 1, 2, −2}. Representa¸˜o gr´fica e diagramas de uma rela¸˜o ca a ca Para o ultimo exemplo dado podemos associar a representa¸˜o gr´fica ´ ca a e o diagrama y 2 1 1 2 x -1 -2 Fun¸˜o ca Fun¸˜o ´ uma rela¸˜o com propriedades especiais. Uma rela¸˜o R do ca e ca ca conjunto A no conjunto B ´ uma fun¸˜o se e ca I) o dom´ ınio da rela¸˜o R, D(R) = A; ca II) para cada elemento x ∈ D(R) existe um unico y ∈ B tal que (x, y) ∈ R ´ III) a imagem da rela¸˜o R, Im(R) ⊂ B. ca Uma rela¸˜o R de A e B que ´ uma fun¸˜o ´ mais comumente represen- ca e ca e tada pela letra f e do seguinte modo: f : A → B, onde, x → y = f (x). Isto significa que, dados os conjuntos A e B, a fun¸˜o tem a lei de correspondˆncia ca e y = f (x). 143 CEDERJ
- 146. Introdu¸˜o `s fun¸oes ca a c˜ Exemplo: Sejam os conjuntos A = {0, 1, 2} e B = {0, 1, 2, 3, 4, 5}; vamos con- siderar a fun¸˜o f : A → B definida por y = x + 1, ou seja, ca f (x) = x + 1 x=0→y =0+1=1 x=1→y =1+1=2 5 x=2→y =2+1=3 • O conjunto A ´ o dom´ e ınio da fun¸˜o. ca • O conjunto {1, 2, 3}, que ´ um subconjunto de B, ´ denominado con- e e junto imagem da fun¸˜o, que indicamos por Im. No exemplo acima, ca Im = {1, 2, 3}. Representa¸˜o de fun¸˜es por diagramas ca co Um diagrama de setas representando uma rela¸˜o de um conjunto A ca em um conjunto B ´ uma fun¸˜o se: e ca (I) De cada elemento de A parte exatamente uma unica seta. ´ (II) Nenhuma seta termina em mais de um elemento de B A B A B é função é função A B A B não é função não é função Representa¸˜o Gr´fica ca a Dados subconjuntos A e B de n´ meros reais e uma fun¸˜o f : A → B, u ca podemos representar a fun¸˜o graficamente como pontos do plano. No eixo ca horizontal representamos o dom´ ınio e no eixo vertical, o contradom´ ınio. CEDERJ 144
- 147. Introdu¸˜o `s fun¸oes ca a c˜ ´ MODULO 1 - AULA 13 Exemplo: A = {−1, 0, 2} e B = {−1, 0, 1, 2, 3, 4} e f (x) = x + 1, vem que y=f(x) 3 x = −1 → y = 0 x=0→y=1 2 x=2→y=3 1 -1 1 2 3 x f = {(−1, 0), (0, 1), (2.3)} e os trˆs pontos assinalados formam o gr´fico da e a fun¸˜o. ca Observa¸˜o sobre gr´ficos: Sabemos que um dos requisitos ao qual uma rela¸˜o ca a ca deve satisfazer para ser uma fun¸˜o, x → y = f (x), ´ que a cada x deve ca e corresponder um unico y. Esta propriedade tem a seguinte interpreta¸˜o: ´ ca toda reta vertical passando pelo dom´ ınio intercepta o gr´fico da fun¸˜o em a ca exatamente um ponto. Exemplos: a) A rela¸˜o f de A em R, f (x) = x2 com A = {x ∈ R | −1 ≤ x ≤ 2}, ca representada abaixo ´ fun¸˜o, pois toda reta vertical passando por pontos de e ca abscissa x ∈ A encontra o gr´fico de f num s´ ponto. a o y -1 2 x b) O gr´fico da rela¸˜o R de A em R representada abaixo x2 + y 2 = 1, onde a ca A = {x ∈ R | −1 ≤ x ≤ 1} n˜o ´ fun¸˜o, pois h´ retas verticais passando a e ca a por pontos de A que encontram o gr´fico de R em dois pontos. a y -1 1 x 145 CEDERJ
- 148. Introdu¸˜o `s fun¸oes ca a c˜ Esbo¸o do Gr´fico de uma Fun¸˜o c a ca Para esbo¸armos o gr´fico cartesiano de uma fun¸˜o f , atribuimos valo- c a ca res convenientes a x no dom´ da fun¸˜o e determinamos os correspondentes ınio ca valores de y = f (x). O gr´fico, ent˜o, ´ constitu´ pelos pontos representa- a a e ıdo tivos dos pares (x, y). Exemplo: (a) Se a fun¸˜o f : A → B, ´ tal que x → y = 2x, onde A = ca e ´ {0, 1, 2, 3}, B = {−1, 0, 2, 4, 6}. E poss´ıvel calcular todos os pontos do gr´fico cartesiano de f . Veja a tabela de valores abaixo. a x 0 1 2 3 y 0 2 4 6 Nesta situa¸˜o, representamos, ponto a ponto, a fun¸˜o. ca ca y 6 5 4 3 2 1 0 1 2 3 x (b) Seja f : R → R x → y = 2x. Para esta fun¸˜o ´ imposs´ construir ca e ıvel uma tabela indicando explicitamente todos os pontos do gr´fico. No en- a tanto podemos, com alguns pontos auxiliares, deduzir a forma do gr´fico f . a Usando os valores j´ calculados na tabela do exemplo a), esbo¸amos o gr´fico. a c a y 2 -1 0 1 x -2 CEDERJ 146
- 149. Introdu¸˜o `s fun¸oes ca a c˜ ´ MODULO 1 - AULA 13 Exerc´ ıcios Resolvidos 1. Seja a fun¸˜o f : R → R ca x → y = x2 − x 1 √ √ a) Calcular f (6), f , f ( 2), f ( 3 − 2). 2 b) Determinar os elementos de D(f ) cuja imagem pela f vale 2. Solu¸˜o: ca a) Para calcularmos a imagem de 6 pela f , basta substituir x por 6 em f (x) = x2 − x, f (6) = 62 − 6 = 30. Do mesmo modo, 2 1 1 1 1 1 1 f = − = − =− , 2 2 2 4 2 4 √ √ 2 √ √ f ( 2) = ( 2) − 2 = 2 − 2 , √ √ √ f ( 3 − 2) = ( 3 − 2)2 − ( 3 − 2) √ √ = 3−4 3+4− 3+2 √ = 9 − 5 3. b) f (x) = 2 ⇒ x2 − x = 2, x2 − x − 2 = 0 √ −b ± b2 − 4ac x= 2a √ 1± 1+8 1±3 x= = 2 2 x1 = 2, x2 = −1 s˜o os dois valores solu¸˜o. a ca x2 − x + 1 2. Seja a fun¸˜o f : [0, ∞) → R dado por f (x) = ca · Calcule x+1 1 √ f (0), f e f ( 2 − 1). 2 Solu¸˜o: ca 02 − 0 + 1 a) f (0) = = 1. 0+1 147 CEDERJ
- 150. Introdu¸˜o `s fun¸oes ca a c˜ 1 ( 2 )2 − 1 + 1 1 2 1 − 1 +1 1−2+4 3 3 2 1 b) f = 1 = 4 1 2 4 = 1+2 = 4 3 = × = . 2 2 +1 2 +1 2 2 4 3 2 √ √ √ ( 2 − 1)2 − ( 2 − 1) + 1 c) f ( 2 − 1) = √ = 2−1+1 √ √ √ 2−2 2+1− 2+1+1 5−3 2 = √ = √ = 2 2 √ √ √ √ 5 2 − 3 2. · 2 5 2−6 = √ √ = . 2· 2 2 3. Sendo f (x) = x2 , f : R → R assinale (V) ou (F): a) f (2) = f (−2) ( ) b) f (1) > f (0) ( ) √ √ √ √ c) f ( 2 + 3) = f ( 2) + f ( 3) − 5 ( ) √ √ √ √ d) f ( 2 · 3) = f ( 2) · f ( 3) ( ) Solu¸˜o: ca f (2) = 22 = 4 a) (V) f (−2) = (−2)2 = 4 ⇒ f (2) = f (−2) f (1) = 12 = 1 b) (V) f (0) = 02 = 0 ⇒ f (1) > f (0) √ √ √ √ √ √ c) (F) f ( 2 + 3) = ( 2 + 3)2 = 2 + 2 6 + 3 = 5 + 2 6 √ √ √ √ f ( 2) + f ( 3) − 5 = ( 2)2 + ( 3)2 − 5 = 2 + 3 − 5 = 0 √ √ √ √ ⇒ f ( 2 + 3) = f ( 2) + f ( 3) − 5 √ √ √ √ √ d) (V) f ( 2 · 3) = ( 2 · 3)2 = ( 6)2 = 6 √ √ √ √ ˙ f ( 2) · f ( 3) = ( 2)2 ( 3)2 = 2 · 3 = 6 √ √ √ √ ⇒ f ( 2 · 3) = f ( 2) · f ( 3) Determina¸˜o de Dom´ ca ınios de Fun¸˜es Num´ricas co e Em geral, quando se define uma fun¸˜o f atrav´s de uma f´rmula (ex.: ca e o 2 2x f (x) = x , f (x) = , etc.), subentende-se que o dom´ınio de defini¸˜o ca x+1 de f , D(f ), ´ o maior subconjunto de R, no qual a defini¸˜o faz sentido (ou e ca onde a fun¸˜o pode operar). ca CEDERJ 148
- 151. Introdu¸˜o `s fun¸oes ca a c˜ ´ MODULO 1 - AULA 13 Exemplos: Defina os dom´ ınios das fun¸˜es abaixo. co x+3 a) f (x) = x−2 Basta impor que o denominador n˜o pode ser nulo: x − 2 = 0 ⇔ x = 2 a Portanto, D(f ) = {x ∈ R | x = 2} = R − {2}. √ b) f (x) = 2x − 6 Em R, o radicando de uma raiz quadrada n˜o pode ser negativo. Por- a tanto, 2x − 6 ≥ 0 ⇔ 2x ≥ 6 ⇔ x ≥ 3 Portanto, D(f ) = {x ∈ R | x ≥ 3} = [3, +∞). √ c) f (x) = 3 2x − 1 O radicando de uma raiz de ´ ındice ´ ımpar pode ser negativo ou nulo ou positivo, ou seja, 2x − 1 pode assumir todos os valores reais. Portanto, D(f ) = R. √ 4 3 − x2 d) f (x) = √ 2x + 1 Como as ra´ızes envolvidas s˜o todas de ´ a ındice par, ´ exigˆncia que os e e radicandos sejam n˜o negativos. Al´m disso, o denominador deve ser a e n˜o nulo. Assim, a 3 − x2 ≥ 0 e 2x + 1 > 0 1 Ou seja, 3 ≥ x2 e x > . 2 Veja as representa¸˜es gr´ficas: co a e -V3 V3 1/2 Portanto a interse¸˜o destes conjuntos determina o dom´ ca ınio. Ou seja 1 √ D(f ) = x∈R| <x≤ 3 2 149 CEDERJ
- 152. Introdu¸˜o `s fun¸oes ca a c˜ Exerc´ ıcios - S´rie A e 1. Sejam A = {x ∈ Z | −2 ≤ x ≤ 2}, B = {x ∈ Z | −6 ≤ x ≤ 6} e a rela¸˜o R = {(x, y) ∈ A × B | x = y + y 2}. Solicita-se: ca a) Enumerar os pares ordenados de R. b) Indicar os conjuntos Dom´ınio e Imagem. 2. Defina os m´ximos subconjuntos de n´ meros reais que s˜o dom´ a u a ınios das fun¸˜es abaixo: co 2x − 3 5 a) f (x) = b) f (x) = x−2 x+2 3. Considere as rela¸˜es G, H, J, M do conjunto A no conjunto B con- co forme os gr´ficos abaixo. Identifique as fun¸˜es. a co relação G relação H y y B B x a x A A relação J relação M y y B B x x A A 4. Seja Z o conjunto dos n´ meros inteiros e sejam os conjuntos A = {x ∈ u Z | −1 < x ≤ 2} e B = {3, 4, 5} se D = {(x, y) ∈ (A × B) | y ≤ x + 4}. Ent˜o: a a) D = A × B b) D tem 2 elementos c) D tem 1 elemento d) D tem 8 elementos e) D tem 4 elementos 4x − 1 5. y = define uma rela¸˜o H ⊂ R × R, onde R s˜o os n´ meros ca a u 2x − 3 reais. Determine o n´ mero real x, tal que (x, 1) ∈ H. u a) x = 0 b) x = 1 c) x = −1 d) x = 5 e) x = −5 CEDERJ 150
- 153. Introdu¸˜o `s fun¸oes ca a c˜ ´ MODULO 1 - AULA 13 6. Determinado-se os pares (x, y) de n´ meros reais que satisfazem `s u a condi¸˜es co x2 + y 2 ≤ 1 , temos: y = x a) 2 pares b) nenhum par c) 3 pares d) infinitos pares e) 1 par 7. Estabelecer se cada um dos esquemas abaixo define ou n˜o uma fun¸˜o a ca de A = {−1, 0, 1, 2} em B = {−2, −1, 0, 1, 2, 3}. Justificar. A B A B R S a) b) -1 -2 -1 -2 0 -1 0 -1 0 1 0 1 1 2 1 2 2 2 3 3 A B A B T V c) d) -1 -2 -1 -2 0 -1 0 -1 0 0 1 1 1 2 1 2 2 2 3 3 8. (UFF-93 1a fase) Considere a rela¸˜o f de M em N, representada no ¯ ca diagrama abaixo: M N x 1 t 4 2 y p 3 z q w 5 r k s Para que f seja uma fun¸˜o de M em N, basta: ca a) apagar a seta (1) e retirar o elemento s b) apagar as setas (1) e (4) e retirar o elemento k c) retirar os elementos k e s d) apagar a seta (4) e retirar o elemento k e) apagar a seta (2) e retirar o elemento k 151 CEDERJ
- 154. Introdu¸˜o `s fun¸oes ca a c˜ 9. (PUC-95) Dentre os 4 desenhos a seguir: y y x x I II y y x x III IV a) Somente I pode ser gr´fico de fun¸˜o da forma y = f (x). a ca b) I, III e IV podem ser gr´ficos de fun¸˜es da forma y = f (x). a co c) Nenhum deles pode ser gr´fico de fun¸˜es da forma y = f (x). a co d) II e IV n˜o podem ser gr´ficos de fun¸˜es da forma y = f (x). a a co e) Nenhuma das respostas acima. 10. (UFF-94-1a fase) O gr´fico que melhor representa a fun¸˜o polinomial ¯ a ca 2 4 p(x) = (x − 1) (x − 4)(x + 9 ) ´: e A) B) y y 0 x 0 x C) D) y y E) y 0 x 0 x x 0 11. Esboce o gr´fico de: a a) y = x2 − 1, D = R b) f (x) = x − 2, sendo D = [−2, 2] CEDERJ 152
- 155. Introdu¸˜o `s fun¸oes ca a c˜ ´ MODULO 1 - AULA 13 12. Determine a e b, de modo que os pares ordenados (2a − 1, b + 2) e (3a + 2, 2b − 6) sejam iguais. 13. Determinar x e y, de modo que: a) (x + 2, y − 3) = (2x + 1, 3y − 1) b) (2x, x − 8) = (1 − 3y, y) c) (x2 + x, 2y) = (6, y 2) 14. Se os conjuntos A e B possuem, respectivamente, 5 e 7 elementos, calcule o n´ mero de elementos de A × B. u 15. (UFF/95 - 1a fase) Em um certo dia, trˆs m˜es deram ` luz em uma ¯ e a a maternidade. A primeira teve gˆmeos; a segunda, trigˆmeos e a ter- e e ceira, um unico filho. Considere, para aquele dia, o conjunto das trˆs ´ e m˜es, o conjunto das seis crian¸as e as seguintes rela¸˜es: a c co I) A que associa cada m˜e a seu filho; a II) A que associa cada filho a sua m˜e; a III) A que associa cada crian¸a a seu irm˜o. c a S˜o fun¸˜es: a co a) somente a I b) somente a II c) somente a III d) todas e) nenhuma 16. (PUC) Entre os gr´ficos abaixo, o unico que pode representar uma a ´ fun¸˜o de vari´vel real ´: ca a e a) y b) y c) y x x x d) y e) y x x 153 CEDERJ
- 156. Introdu¸˜o `s fun¸oes ca a c˜ 17. (UERJ/93) A fun¸˜o f definida no conjunto dos inteiros positivos por: ca n , se n for par f (n) = 2 3n + 1, se n for ´ımpar O n´ mero de solu¸˜es da equa¸˜o f (n) = 25 ´: u co ca e a) zero b) um c) dois d) quatro e) infinito 18. (UFC-CE) Qual dos gr´ficos a seguir n˜o pode representar uma fun¸˜o? a a ca a) y b) y c) y d) y e) y 19. (FGV-SP) Considere a seguinte fun¸˜o de vari´vel real ca a 1 se x ´ racional e f (x) = 0 se x ´ irracional e Podemos afirmar que: a) f (2, 3) = 0 b) f (3, 1415) = 0 c) 0 ≤ f (a) + f (b) + f (c) ≤ 3 d) f [f (a)] = 0 e) f (0) + f (1) = 1 20. (SANTA CASA-82) Seja f uma fun¸˜o de Z em Z, definida por ca 0, se x ´ par e f (x) = 1, se x ´ ´ e ımpar Nestas condi¸˜es, pode-se afirmar que: co a) f ´ injetora e n˜o sobrejetora e a b) f ´ sobrejetora e n˜o injetora e a c) f (−5) · f (2) = 1 d) f (f (x)) = 0, ∀ x ∈ R e) O conjunto-imagem de f ´ {0, 1} e CEDERJ 154
- 157. Introdu¸˜o `s fun¸oes ca a c˜ ´ MODULO 1 - AULA 13 21. (FUVEST-82) O n´ mero real α ´ solu¸˜o simultˆnea das equa¸˜es u e ca a co f (x) = 0 e g(x) = 0 se e somente se α ´ raiz da equa¸˜o: e ca a) f (x) + f (x) = 0 b) [f (x)]2 + [g(x)]2 = 0 c) f (x) · g(x) = 0 d) [f (x)]2 − [g(x)]2 = 0 e) f (x) − g(x) = 0 ˜ e 22. (PUC-93) Entre as fun¸˜es T : R2 → R2 abaixo, NAO ´ injetora a co definida por: a) T (x, y) = (x, 0) b) T (x, y) = (y, x) c) T (x, y) = (2x, 2y) d) T (x, y) = (−y, x) e) T (x, y) = (x + 1, y + 1) Exerc´ ıcios - S´rie B e 1. (UNIFICADO-92) Qual dos gr´ficos abaixo representa, em R2 as solu¸˜es a co 2 2 da equa¸˜o y = x(x − 1). ca A) B) C) D) E) y y y y y x x x x x 2. (IBEMEC 98) Considere a fun¸˜o f , de R em R, tal que f (x + 1) = ca f (x) + 2 e f (2) = 3. Ent˜o, f (50) ´ igual a: a e a) 105 b) 103 c) 101 d) 99 e) 97 3. (FUVEST-SP) Seja f uma fun¸˜o tal que f (x + 3) = x2 + 1 para todo ca x real. Ent˜o f (x) ´ igual a: a e a) x2 − 2 b) 10 − 3x c) −3x2 + 16x − 20 d) x2 − 6x + 10 e) x2 + 6x − 16 155 CEDERJ
- 158. Introdu¸˜o `s fun¸oes ca a c˜ x 4. (UGF-96-2o Sem.) Se f (3x) = ¯ + 1 ent˜o f (x − 1) ´ igual a: a e 2 x+5 3x − 1 5x + 3 3x a) b) c) d) e) 3x − 2 6 2 2 2 2 · f (n) + 1 5. Se f (n + 1) = para n = 1, 2, 3, . . . e se f (1) = 2, ent˜o o a 2 valor de f (101) ´: e a) 49 b) 50 c) 53 d) 52 e) 51 6. (FUVEST/93) Uma fun¸˜o de vari´vel real satisfaz a condi¸˜o ca a ca f (x+1) = f (x)+f (1), qualquer que seja o valor da vari´vel x. Sabendo a que f (2) = 1 podemos concluir que f (5) ´ igual a: e 1 5 a) b) 1 c) d) 5 e) 10 2 3 7. (UFF/96) Para a fun¸˜o f : N∗ → N∗ , que a cada n´ mero natural n˜o- ca u a nulo associa o seu n´ mero de divisores, considere as afirmativas: u I) existe um n´ mero natural n˜o-nulo n tal que f (n) = n. u a II) f ´ crescente e III) f n˜o ´ injetiva. a e Assinale a op¸˜o que cont´m a(s) afirmativa(s) correta(s): ca e a) apenas II b) apenas I e III c) I, II e III d) apenas I e) apenas I e II 8. (UFMG) A fun¸˜o f : R → R associa a cada n´ mero real x o me- ca u 1 2 nor inteiro maior do que 2x. O valor de f (−2) + f − +f ´: e 5 3 9. (UFRJ/93) Uma fun¸˜o f (x) tem o seguinte gr´fico: ca a Considere agora uma nova fun¸˜o g(x) = f (x + 1). ca a) Determine as ra´ da equa¸˜o g(x) = 0 ızes ca b) Determine os intervalos do dom´ ınio de g(x) nos quais esta fun¸˜o ´ ca e estritamente crescente. CEDERJ 156
- 159. Introdu¸˜o `s fun¸oes ca a c˜ ´ MODULO 1 - AULA 13 10. (CESGRANRIO) Seja f (x) a fun¸˜o que associa, a cada n´ mero real ca u x, o menor dos n´ meros (x + 1) e (−x + 5). Ent˜o o valor m´ximo de u a a f (x) ´: e a) 1 b) 3 c) 4 d) 5 e) 7 11. Definimos: f : N → N f (0) = 1 f (n + 1) = 2f (n) Calcule f (3). 12. (FEI-73) Chama-se ponto fixo de uma fun¸˜o f um n´ mero real x tal ca u 1 que f (x) = x. Os pontos fixos da fun¸˜o f (x) = 1 + s˜o: ca a x a) x = ±1 √ 1± 5 b) x = 2 c) n˜o tem ponto fixo a d) tem infinitos pontos fixos 13. (PUC-92) Um reservat´rio tem a forma de um cone de revolu¸˜o de eixo o ca vertical e v´rtice para baixo. Enche-se o reservat´rio por interm´dio e o e de uma torneira de vaz˜o constante. O gr´fico que melhor representa a a o n´ da ´gua em fun¸˜o do tempo, contado a partir do instante em ıvel a ca que a torneira foi aberta ´: e A) B) nível nível tempo tempo C) D) E) nível nível nível tempo tempo tempo 157 CEDERJ
- 160. Introdu¸˜o `s fun¸oes ca a c˜ Gabarito S´rie A e 1. a) R = {(2, −2), (0, −1), (0, 0), (2, 1)}. b) D(R) = {0, 2}, Im(R) = {−2, −1, 0, 1}. 2. a) D(f ) = {x ∈ R | x = 2} = (−∞, 2) ∪ (2, ∞). b) D(f ) = {x ∈ R | x > −2} = (−2, ∞). 3. Apenas G ´ fun¸˜o. 4. d) e ca 5. c) 6. d) 7. a) n˜o b) n˜o c) sim d) sim. 8. d) 9.b) 10. d) a a 11. 12. a = −3; b = 8 13. a) x = 1 e y = −1 b) x = 5 e y = −3, √ c) x = −3 ou x = 2 e y = 0 ou y = 2, d) x = ±2 e y = ± 3. 14. 35 15. b) 16. d) 17. b) 18. c) 19. c) 20. e) 21. b) 22. a) S´rie B e 1. a) 2. d) 3 d) 4. a) 5. d) 6. c) 7. b) 8. -2 9. a) x ∈ {−2, 0, 3} b) (−3, −1) e (0,1) 10. b) 11. f (3) = 16 12. b) 13. b) Auto-avalia¸˜o ca Antes de passar ` aula seguinte, vocˆ deve resolver todos os exerc´ a e ıcios da S´rie A. A S´rie B fica como exerc´ de aprofundamento. e e ıcio CEDERJ 158
- 161. Fun¸oes composta e inversa c˜ ´ MODULO 1 - AULA 14 Aula 14 – Fun¸˜es composta e inversa co Objetivos: S˜o objetivos desta aula possibilitar que vocˆ: a e • Entenda e trabalhe com o conceito de fun¸˜o composta. ca • Possa decidir quando uma fun¸˜o possui ou n˜o inversa. ca a • Entenda os conceitos de fun¸˜o sobrejetiva, injetiva e bijetiva e de ca fun¸˜o inversa. ca • Possa resolver problemas envolvendo fun¸˜es inversas e possa represen- co tar graficamente as solu¸˜es. co Fun¸˜o composta ca Considere f uma fun¸˜o do conjunto A no conjunto B e g uma fun¸˜o ca ca do conjunto B no conjunto C. Ent˜o a fun¸˜o h de A em C, h a fun¸˜o a ca ca composta de f e g, pode ser definida por h(x) = g(f (x)). Nota¸˜o: h = g ◦ f . ca No diagrama abaixo est´ representada a composi¸˜o de f em g. a ca f g A −→ B −→ C g◦f Exemplos (i) Se ent˜o h = g ◦ f ´ tal que a e A 0 h a b 1 c 2 d 159 CEDERJ
- 162. Fun¸oes composta e inversa c˜ (ii) Suponha Z o conjunto dos n´ meros inteiros, f : Z → Z f (x) = x − 2 u g: Z → Z g(x) = x3 ent˜o a fun¸˜o composta h : Z → Z pode ser calculada por a ca h(x) = g(f (x)) h(x) = g(x − 2) h(x) = (x − 2)3 Exerc´ ıcios resolvidos (i) Sejam as fun¸˜es f : R → R e g : R → R definidas por f (x) = x2 − 1 e co g(x) = x + 3. a) obter a fun¸˜o composta h = g ◦ f e m = f ◦ g ca b) calcule h(2) e m(−3) c) existem valores x ∈ R tais que h(x)=0? Solu¸˜o: ca a) h(x) = g(f (x)) = g(x2 − 1) = x2 − 1 + 3 h(x) = x2 + 2 m(x) = f (g(x)) = f (x + 3) = (x + 3)2 − 1 m(x) = x2 + 6x + 9 − 1 = x2 + 6x + 8 b) h(2) = 22 + 2 = 4 m(−3) = (−3)2 + 6(−3) + 8 m(−3) = 9 − 18 + 8 = −1 c) h(x) = 0 ⇔ x2 +2 = 0 (esta equa¸˜o n˜o tem solu¸˜o x ∈ R). Resposta: ca a ca N˜o. a √ (ii) Sejam f : R → R e g : R → R. Sabendo-se que f (x) = 5 + x2 e que a √ imagem da fun¸˜o f ◦ g ´ o intervalo real [+ 5, +3], a alternativa que ca e representa a imagem da fun¸˜o g ´: ca e √ a) [+ 5, +3] b) [−2. + 2] √ √ c) [−2, + 5] d) [− 5, +2] √ √ e) [− 5, + 5] CEDERJ 160
- 163. Fun¸oes composta e inversa c˜ ´ MODULO 1 - AULA 14 Solu¸˜o: ca g f Im(fog) R R V5 3. R √ f ◦ g(x) = f (g(x)) = 5 + g 2(x). Logo 5 ≤ 5 + g 2 (x) ≤ 3 ⇒ 5 ≤ 5 + g 2(x) ≤ 9 Ent˜o 0 ≤ g 2(x) ≤ 4. Os valores de g(x) que verificam a desigualdade a acima s˜o −2 ≤ g(x) ≤ 2. a Logo, Im g(x) = [−2, 2]. Resposta b). (iii) Sejam as fun¸˜es f : R → R e g : R → R definidas por co x2 se x ≥ 0 f (x) = g(x) = x − 3. x se x < 0 Encontre a express˜o que define f ◦ g = h. a Solu¸˜o: h(x) = f (g(x)) = f (x − 3). ca Em virtude da defini¸˜o de f precisamos saber quando x − 3 ≥ 0 e ca quando x − 3 < 0. Ora x − 3 ≥ 0 ⇔ x ≥ 3 e x − 3 < 0 ⇔ x < 3. (x − 3)2 se x ≥ 3 Logo h(x) = x − 3 se x < 3 (iv) Sejam as fun¸˜es reais g(x) = 3x+2 e (f ◦g)(x) = x2 −x+1. Determine co a express˜o de f . a Solu¸˜o: ca (f ◦ g)(x) = f (g(x)) = f (3x + 2) = x2 − x + 1 y−2 Fa¸amos agora 3x + 2 = y ⇒ x = c 3 Logo, 2 y−2 y−2 f (y) = − +1 3 3 y 2 − 4y + 4 y − 2 f (y) = − +1 9 3 1 f (y) = [y 2 − 4y + 4 − 3(y − 2) + 9] 9 1 f (y) = [y 2 − 7y + 19] 9 161 CEDERJ
- 164. Fun¸oes composta e inversa c˜ Fun¸˜es sobrejetora, injetora e bijetora co Uma fun¸˜o f : A → B ´ sobrejetora se Im(f ) = B. Isto para todo ca e elemento y ∈ B existe x ∈ A tal que f (x) = y. Uma fun¸˜o g : A → B ´ injetora (ou injetiva) se elementos diferentes ca e x1 e x2 do dom´ ınio A d˜o como imagens elementos g(x1 ) e g(x2 ) tamb´m a e diferentes. Isto ´, vale a propriedade: e x1 , x2 ∈ A, x1 = x2 ⇒ g(x1 ), g(x) ∈ Im(g) e g(x1 ) = g(x2 ). Uma fun¸˜o f : A → B que tem ambas as propriedades injetora e so- ca brejetora, ´ dita uma fun¸˜o bijetora. e ca Exemplos: Sejam A = {0, 1, 2}, B = {1, 2, 3} e f, g : A → B como nos diagramas abaixo. A fun¸˜o f n˜o ´ injetora, nem sobrejetora. A fun¸˜o g ´ bijetora. ca a e ca e f g A B A B 0 1 0 1 1 2 1 2 2 3 2 3 D=A D=A Im = B Im = B Identifica¸˜o a partir do gr´fico se uma fun¸˜o ´ sobrejetora, inje- ca a ca e tora ou bijetora Seja y = f (x) uma fun¸˜o. Considere seu gr´fico, representado abaixo. ca a Se as retas paralelas a Ox e passando pelo contradom´ ınio de f encon- tram o gr´fico de f em pelo menos um ponto, f ´ sobrejetora. a e CEDERJ 162
- 165. Fun¸oes composta e inversa c˜ ´ MODULO 1 - AULA 14 Se as retas paralelas a Ox encontram o gr´fico de f no m´ximo em um a a ponto, f ´ injetora. e y CD(f)=Im f x 0 D(f) Se as retas paralelas a Ox e passando pelo contradom´ ınio de f encon- tram o gr´fico de f em exatamente um s´ ponto, f ´ bijetora. a o e y f Im(f) x 0 D(f) Fun¸˜o inversa ca Uma fun¸˜o f : A → B ´ uma rela¸˜o entre os conjuntos A e B com ca e ca propriedades especiais. f como rela¸˜o ´ um subconjunto de A×B. Os pares ca e ordenados (x, y) deste subconjunto s˜o tais que y = f (x). a Por exemplo, se A = {−1, 1, 2}, B = {−1, 0, 1, 4} e f (x) = x2 . Enquanto rela¸˜o, f se escreve como f = {(−1, 1), (1, 1), (2.4)}. Suponha ca que as coordenadas s˜o trocadas para obter uma nova rela¸ao g. a c˜ g = {(1, −1), (1, 1), (4, 2)}. Em que condi¸˜es podemos garantir que, ap´s a invers˜o, g ´ ainda uma co o a e fun¸˜o (e n˜o meramente uma rela¸˜o?) Nos casos afirmativos g ´ chamada ca a ca e −1 fun¸˜o inversa de f e geralmente denotada por f . ca Se vocˆ pensar um pouquinho vai chegar ` conclus˜o de que g ´ uma e a a e nova fun¸˜o apenas no caso em que a fun¸˜o f for bijetora. Entre outras ca ca palavras, somente as fun¸˜es bijetoras f possuem uma inversa f −1 . co Vamos tentar te convencer da validade desta resposta atrav´s de dia- e gramas. 163 CEDERJ
- 166. Fun¸oes composta e inversa c˜ Caso (I): Se f n˜o ´ injetora ent˜o n˜o existe inversa. Veja um exemplo, a e a a representado no diagrama a seguir, onde A = {a, b, c} e B = {1, 2} A fun¸˜o inversa n˜o pode ser definida para o elemento 1, pois f (a) = ca a f (b) = 1. Caso (II): Se f n˜o ´ sobrejetora ent˜o n˜o existe inversa. Veja um exemplo, a e a a representado no diagrama abaixo, onde A = {a, b, c} e B = {1, 2, 3, 4} A fun¸˜o inversa n˜o pode ser definida em 4 ∈ B. ca a f −1 (4) =? Portanto, uma fun¸˜o f : A → B, possui a fun¸˜o inversa f −1 se e ca ca somente se f ´ bijetora. e Seja f : A → B uma fun¸˜o bijetora. Ent˜o a fun¸˜o inversa f −1 : B → ca a ca A tem as seguintes propriedades: (i) f −1 ´ uma fun¸˜o bijetora de B em A. e ca (ii) D(f −1 ) = Im(f ) = B. (iii) Im(f −1 ) = D(f ) = A. A rela¸˜o entre os pares ordenados de f e f −1 pode ser expressa simbolica- ca mente por (x, y) ∈ f ⇔ (y, x) ∈ f −1 ou y = f (x) ⇔ x = f −1 (y) CEDERJ 164
- 167. Fun¸oes composta e inversa c˜ ´ MODULO 1 - AULA 14 Exemplos. (i) Qual a fun¸˜o inversa da fun¸˜o bijetora f : R → R definida ca ca por f (x) = 3x + 2? Solu¸˜o: se y = f (x) ent˜o f −1 (y) = x. ca a Partindo de y = f (x), y = 3x + 2, procuramos isolar x. y−2 y = 3x + 2 ⇒ x = 3 −1 y−2 Logo, f (y) = x = 3 Nota: Como a vari´vel pode indiferentemente ser trocada tamb´m podemos a e escrever x−2 f −1 (x) = 3 (ii) Qual ´ a fun¸˜o inversa da fun¸˜o bijetora em f : R → R definida por e ca ca f (x) = x3 ? √ Solu¸˜o: y = f (x) = x3 , logo, x = 3 y. ca √ √ Portanto f −1 (y) = x = 3 y. Ou seja, f −1 (x) = 3 x. (iii) Um exemplo importante ´ o da fun¸˜o identidade. I : R → R, I(x) = x. e ca Isto ´, se escrevermos y = I(x), temos que y = x. A representa¸˜o gr´fica e ca a desta fun¸˜o resulta na bissetriz do primeiro quadrante. Veja a figura abaixo. ca y y=x 2 2 x ´ E claro que I −1 = I. Isto ´, a fun¸˜o identidade e sua inversa coincidem. e ca Observa¸˜es Importantes co (i) Um exame do gr´fico abaixo nos leva ` conclus˜o que os pontos (x, y) a a a e (y, x) do plano, abaixo representados, s˜o sim´tricos com rela¸˜o ` reta a e ca a y = x. (x,y) y=x y x (y,x) 0 x y 165 CEDERJ
- 168. Fun¸oes composta e inversa c˜ Lembrando a rela¸˜o ca (x, y) ∈ f ⇔ (y, x) ∈ f −1 podemos concluir que, no plano, os pontos que representam uma fun¸˜o e ca sua inversa s˜o sim´tricos em rela¸˜o ` reta y = x. Isto ´, os gr´ficos que a e ca a e a representam f e f s˜o sim´tricos em rela¸˜o ` reta bissetriz do 1o e 4o −1 a e ca a ¯ ¯ quadrante. (ii) Sejam f : A → B e a fun¸˜o inversa f −1 : B → A. Ent˜o f ◦ f −1 : B → B ca a −1 e f ◦ f : A → A s˜o fun¸˜es identidade. De fato a co y = f (x) ⇔ x = f −1 (y), implica que f ◦ f −1 (y) = f (x) = y e ent˜o f ◦ f −1 = Id. a Tamb´m e f −1 ◦ f (x) = f −1 (y) = x e ent˜o f −1 ◦ f = Id. a Exemplo: Seja a fun¸˜o f em R definida por f (x) = 2x − 3. Construir num mesmo ca plano cartesiano os gr´ficos de f e f −1 . a Solu¸˜o: ca x+3 f (x) = 2x − 3 f −1 (x) = 2 x y x y -1 -5 -5 -1 0 -3 -3 0 1 -1 -1 1 2 1 1 2 3 3 3 3 4 5 5 4 y f y=x f-1 x CEDERJ 166
- 169. Fun¸oes composta e inversa c˜ ´ MODULO 1 - AULA 14 Exerc´ ıcios - S´rie A e 1. Dados f (x) = x2 − 1, g(x) = 2x. Determine: a) f ◦ g(x) b) f ◦ f (x) c) g ◦ f (x) d) g ◦ g(x). 2. (UFF 96 - 2a fase) Sendo f a fun¸˜o real definida por f (x) = x2 −6x+8, ¯ ca para todos os valores x > 3. Determine o valor de f −1 (3). 3. (UNI-RIO 97 - 1a fase) A fun¸˜o inversa da fun¸˜o bijetora f : R − ¯ ca ca 2x − 3 {−4} → R − {2} definida por f (x) = ´: e x+4 x+4 x−4 4x + 3 a) f −1 (x) = b) f −1 (x) = c) f −1 (x) = 2x + 3 2x − 3 2−x −1 4x + 3 −1 4x + 3 d) f (x) = e) f (x) = x−2 x+2 4. (UFF 2001) Dada a fun¸˜o real de vari´vel real f , definida por ca a x+1 f (x) = , x = 1: x−1 a) determine (f ◦ f )(x) b) escreva uma express˜o para f −1 (x). a 5. (UFRS - 81) Se P (x) = x3 − 3x2 + 2x, ent˜o {x ∈ R | P (x) > 0} ´: a e a) (0,1) b) (1,2) c) (−∞, 2) ∪(2, ∞) d) (0, 1) ∪(2, ∞) e) (−∞, 0) ∪(1, 2). 6. Se f (x) = 3x , ent˜o f (x + 1) − f (x) ´: a e a) 3 b) f (x) c) 2f (x) d) 3f (x) e) 4f (x) 7. (FUVEST SP) Se f : R → R ´ da forma f (x) = ax + b e verifica e f [f (x)] = x + 1, para todo real, ent˜o a e b valem, respectivamente: a 1 1 a) 1 e b) −1 e c) 1 e 2 d) 1 e −2 e) 1 e 1 2 2 8. (FATEC SP) Seja a fun¸˜o f tal que f : (R − {−2}) → R, onde ca x−2 f (x) = · O n´ mero real x que satisfaz f (f (x)) = −1 ´: u e x+2 a) −4 b) −2 c) 2 d) 4 e) n.d.a. 9. Determine o dom´ ınio de cada fun¸˜o: ca √ √ I) f (x) = |x| II) f (x) = x2 − 4 III) f (x) = 1/x IV) f (x) = x/x 167 CEDERJ
- 170. Fun¸oes composta e inversa c˜ 10. Nos gr´ficos abaixo determine D(f ) e Im(f ) a I) II) y y 12 f 1 f 2 -5 0 1 x 1 3 x -1 3x + 5 11. Se f (x + 1) = (x = −1/2), o dom´ ınio de f (x) ´ o conjunto dos e 2x + 1 n´ meros reais x tais que: u a) x = 1/2 b) x = −1/2 c) x = −5/3 d) x = 5/3 e) x = −3/5 Exerc´ ıcios - S´rie B e 1. Sejam as fun¸˜es reais g(x) = 2x − 2 e (f ◦ g)(x) = x2 − 2x. Determine co a express˜o de f . a 2. (UFF 96 - 2a fase) Dadas as fun¸˜es reais de vari´vel real f e g definidas ¯ co a √ por f (x) = x2 − 4x + 3, com x ≥ 2 e g(x) = 2 + 1 + x, com x ≥ −1, determine: a) (g ◦ f )(x) b) f −1 (120) √ 3. Dada a fun¸˜o f (x) = ca 9 − x2 , para qualquer n´ mero real x, tal que u |x| ≥ 3, tem-se: 1 a) f (3x) = 3f (x) b) f (0) = f (3) c) f −1 (x) = f , se x = 0 x d) f (−x) = f (x) e) f (x − 3) = f (x) − f (3) 4. (CE.SESP-81) Seja f : N → Z, a fun¸˜o definida por ca f (0) = 2 f (1) = 5 f (n + 1) = 2f (n) − f (n − 1) o valor de f (5) ´: e a) 17 b) 6 c) 5 d) 4 e) 10 CEDERJ 168
- 171. Fun¸oes composta e inversa c˜ ´ MODULO 1 - AULA 14 5. (MACK SP) Sendo f (x − 1) = 2x + 3 uma fun¸˜o de R em R, a fun¸˜o ca ca inversa f −1 (x) ´ igual a: e x−3 a) (3x+1)·2−1 b) (x−5)·2−1 c) 2x+2 d) e) (x+3)·2−1 2 6. (CESGRANRIO) Considere as fun¸˜es co f: R→R g: R → R x → 2x + b x → x2 onde b ´ uma constante. Conhecendo-se a composta e g◦f: R→ R x → g(f (x)) = 4x2 − 12x + 9 podemos afirmar que b ´ um elemento do conjunto: e a) (−4, 0) b) (0,2) c) (2,4) d) (4, +∞) e) (−∞, −4) 7. Considere a fun¸˜o f : N → N definida por: ca x , se x ´ par e 2 f (x) = x + 1 , se x ´ ´ e ımpar 2 onde N ´ o conjunto dos n´ meros naturais. Assinale a alternativa e u verdadeira: a) A fun¸˜o f ´ injetora. ca e b) A fun¸˜o f n˜o ´ sobrejetora. ca a e c) A fun¸˜o f ´ bijetora. ca e d) A fun¸˜o f ´ injetora e n˜o ´ sobrejetora. ca e a e e) A fun¸˜o f ´ sobrejetora e n˜o ´ injetora. ca e a e x+1 8. O dom´ ınio da fun¸˜o y = ca ´ o conjunto: e x2 − 3x + 2 a) {x ∈ R | −1 ≤ x < 1 ∨ x > 2} b) {x ∈ R | −1 ≤ x ≤ 1 ∨ x ≥ 2} c) {x ∈ R | x ≤ −1 ∧ x ≥ 2} d) {x ∈ R | −1 ≤ x ≤ 1} e) ∅ 169 CEDERJ
- 172. 9. (CESGRANRIO-79) Seja f : (0; +∞) → (0; +∞) a fun¸˜o dada por ca 1 f (x) = 2 e f −1 a fun¸˜o inversa de f . O valor de f −1 (4) ´: ca e x a) 1/4 b) 1/2 c) 1 d) 2 e) 4 1 10. (UFMG-80) Seja f (x) = · Se x = 0, uma express˜o para f (1/x) a x2 +1 ´: e x2 + 1 x2 1 1 a) x2 + 1 b) c) d) +x e) x2 x2 + 1 x2 x2 + 1 11. Considere a fun¸˜o F (x) = |x2 − 1| definida em R. Se F ◦ F representa ca a fun¸˜o composta de F com F , ent˜o: ca a a) (F ◦ F )(x) = x|x2 − 1|, ∀ x ∈ R b) ∃ y ∈ R | (F ◦ F )y = y c) F ◦ F ´ injetora e d) (F ◦ F )(x) = 0 apenas para 2 valores reais de x e) todas as anteriores s˜o falsas. a Gabarito S´rie A e 1. a) f ◦ g(x) = 4x2 − 1 b) f ◦ f (x) = x4 − 2x2 c) g ◦ f (x) = 2x2 − 2 x+1 d) g ◦ g(x) = 4x 2. 5 3. c) 4. a) (f ◦ f )(x) = x b) f −1 (x) = x−1 5. d) 6. c) 7. a) 8. c) 9. I) R, II) {x ∈ R | x ≤ −2 e x ≥ 2}, III) R∗ , IV) R∗ 10. I) D(f ) = [−5, 1], Im(f ) = [0, 12] II) D(f ) = [0, 3], + Im(f ) = [−1, 2] 11. a) S´rie B e 1 1. f (x) = x2 − 1 2. a) (g ◦ f )(x) = x b) 13 3. d) 4. a) 5. b) 4 6. a) 7. e) 8. a) 9. b) 10. c) 11. e) Auto-avalia¸˜o ca Antes de passar ` aula seguinte, vocˆ deve resolver todos os exerc´ a e ıcios da S´rie A. A S´rie B fica como exerc´ de aprofundamento. e e ıcio
- 173. o Fun¸˜o do 1¯ grau ca ´ MODULO 1 - AULA 15 Aula 15 – Fun¸˜o do 1o grau ca ¯ Objetivos: Ap´s estudar esta aula, vocˆ saber´: o e a • Reconhecer uma fun¸˜o linear afim, identificar o coeficiente angular e ca representar graficamente no plano. • Identificar se a fun¸˜o linear afim ´ crescente ou decrescente e descrever ca e os pontos do dom´ ınio onde a fun¸˜o ´ positiva ou negativa. ca e Defini¸˜o ca Uma fun¸˜o f : R → R dada por f (x) = ax + b, onde a e b s˜o n´ meros ca a u o reais e a = 0 ´ chamada de fun¸˜o polinomial do 1¯ grau (ou fun¸˜o linear e ca ca afim). O n´ mero a ´ chamado coeficiente angular e b coeficiente linear da u e fun¸˜o. ca Representa¸˜o gr´fica ca a Seja y = f (x) = ax + b. Ent˜o a x=0→y=b b x=− →y=0 a b e os pontos (0, b) e − , 0 definem uma reta no plano. Esta reta ´ o gr´fico e a a de f . Suponha para a representa¸˜o abaixo que a > 0 e b > 0. ca Q P A O Observe na figura os triˆngulos retˆngulos AOb e bP Q, ambos com a a ˆngulo agudo θ. N´s ainda n˜o revisamos trigonometria, mas provavelmente a o a vocˆ sabe que podemos calcular a tangente do ˆngulo θ usando os triˆngulos. e a a 171 CEDERJ
- 174. o Fun¸˜o do 1¯ grau ca Ob QP Assim tg θ = e tg θ = . Isto ´, e OA bP b y−b tg θ = b = a e tg θ = . a x Juntando as equa¸˜es vem que co y−b a= ⇒ y = ax + b. x Nota: (i) Segundo o gr´fico da fun¸˜o linear f (x) = ax + b, o coeficiente a ca linear b da reta gr´fico de f ´ o valor da ordenada do ponto de interse¸˜o da a e ca reta com o eixo Oy. (ii) O valor a d´ origem ` equa¸˜o a = tg θ, onde θ ´ a inclina¸˜o do gr´fico a a ca e ca a de f . temos dois casos a) 0 < θ < 90◦ ⇒ tg θ > 0 e a > 0 logo f ´ fun¸˜o crescente. e ca b) 90◦ < θ < 180◦ ⇒ tg θ < 0 e a < 0 logo f ´ fun¸˜o decrescente. e ca y=f(x) y=f(x) θ θ x x a>0 a<0 Exerc´ ıcios resolvidos (i) Construa o gr´fico da fun¸˜o linear f (x) = −x + 3. a ca Solu¸˜o: Precisamos determinar apenas dois pontos (x, y) do gr´fico ca a y = f (x) = −x + 3 x=0 ⇒ y=3 x=3 ⇒ y=0 Ent˜o (0,3) e (3,0) s˜o pontos do gr´fico. a a a y 3 2 1 1 2 3 x CEDERJ 172
- 175. o Fun¸˜o do 1¯ grau ca ´ MODULO 1 - AULA 15 (ii) Determine a equa¸˜o da reta y = ax + b cujo gr´fico est´ abaixo. ca a a y 30º x -3 √ √ 3 3 Solu¸˜o: Como tg 30◦ = ca este ´ o valor de a. Logo, y = f (x) = e x + b. 3 √3 3 Para achar b, usamos que (0, −3) ´ ponto do gr´fico. Ent˜o −3 = e a a ×0+b √ 3 3 e b = −3. Logo f (x) = x − 3. 3 Estudo do sinal de y = f (x) = ax + b Queremos estudar a varia¸˜o do sinal de y = f (x) quando x varia. ca Vamos dividir em dois casos. Caso A: a > 0. b y = ax + b = 0 ⇔ x = − a b y = ax + b > 0 ⇔ x > − a b y = ax + b < 0 ⇔ x < − a b O gr´fico mostra que para x > − o valor y = f (x) ´ positivo e para a e a b x < − , y = f (x) ´ negativo. e a y + - -b x a Caso B: a < 0 b y = ax + b = 0 ⇔ x = − a b y = ax + b > 0 ⇔ x < − a b y = ax + b < 0 ⇔ x > − a 173 CEDERJ
- 176. o Fun¸˜o do 1¯ grau ca b O gr´fico de y = f (x) = ax + b, mostra que para x < − o valor a a b y = f (x) ´ positivo e para x > − o valor y = f (x) ´ negativo. e e a y=f(x) + -b - x a Exerc´ ıcios resolvidos Resolva as inequa¸˜es abaixo: co a) 3x − 2 < 0 b) −x + 1 > 0 c) (3x + 6)(−2x + 8) > 0 x+3 d) ≤2 2x + 1 Solu¸˜o: ca 2 (a) 3x − 2 < 0 ⇔ 3x < 2 ⇔ x < 3 2 2 O conjunto solu¸˜o S = ca x∈R|x< = −∞, 3 3 (b) −x + 1 > 0 ⇔ −x > −1 ⇔ x < 1. O conjunto solu¸˜o ´ S = {x ∈ R | x < 1} = (−∞, 1). ca e (c) A inequa¸˜o ´ um produto e para resolvˆ-la ´ eficiente fazer uma tabela. ca e e e Primeiro encontramos as ra´ de ızes y = 3x + 6 → raiz x = −2 y = −2x + 8 → raiz x = 4 e constru´ ımos a tabela -2 4 R 3x + 6 > 0 ⇔ x > −2 3x+6 + + 3x + 6 < 0 ⇔ x < −2 -2x+8 + (3x+6)(-2x+8) + + −2x + 8 > 0 ⇔ x > 4 −2x + 8 < 0 ⇔ x < 4. CEDERJ 174
- 177. o Fun¸˜o do 1¯ grau ca ´ MODULO 1 - AULA 15 Com os dados anteriores, e usando que o produto de n´ meros de mesmo u sinal ´ positivo e o produto de n´ meros de sinais contr´rios ´ negativo, e u a e completamos a tabela. Logo, o conjunto solu¸˜o ca S = (−∞, −2) ∪ (4, ∞) (d) Antes de resolver temos que reduzir o segundo membro a zero: x+3 x + 3 − 2(2x + 1) −2≤0 ⇔ ≤0 2x + 1 2x + 1 −3x + 1 ⇔ ≤ 0. 2x + 1 Esta ultima inequa¸˜o ´ equivalente ` inequa¸˜o proposta inicialmente ´ ca e a ca e tem forma pr´pria para resolvermos. Vamos construir a tabela o 1 −3x + 1 > 0 ⇔ −3x > −1 ⇔ x < 3 1 −3x + 1 > 0 ⇔ −3x < −1 ⇔ x > 3 −1 2x + 1 > 0 ⇔ x > 2 −1 2x + 1 < 0 ⇔ x < 2 -1/2 -1/3 R -3x+1 + + 2x+1 + + -3x+1 + 2x+1 −3x + 1 Na inequa¸˜o quociente ca ≥ 0 procuramos os valores de x que 2x + 1 tornam o primeiro membro positivo ou nulo. O conjunto solu¸˜o ´ ca e 1 1 S= − , 2 3 1 1 Nota: O valor x = anula o numerador e ´ solu¸˜o. O valor x = − e ca 3 2 anula o denominador. Como o denominador nunca pode ser zero, este valor deve ser exclu´ do conjunto solu¸˜o. ıdo ca 175 CEDERJ
- 178. o Fun¸˜o do 1¯ grau ca Exerc´ ıcios - S´rie A e 1. (UFRJ 98) O gr´fico a seguir descreve o crescimento populacional de a certo vilarejo desde 1910 at´ 1990. No eixo das ordenadas, a popula¸˜o e ca ´ dada em milhares de habitantes. e população 10 9 8 7 6 5 4 3 2 1910 1920 1930 1940 1950 1960 1970 1980 1990 ano a) Determine em que d´cada a popula¸˜o atingiu a marca de 5.000 habi- e ca tantes. b) Observe que a partir de 1960 o crescimento da popula¸˜o em cada ca d´cada tem se mantido constante. Suponha que esta taxa se mantenha e no futuro. Determine em que d´cada o vilarejo ter´ 20.000 habitantes. e a 2. Determinar o valor de m para que o gr´fico da fun¸˜o y = f (x) = a ca 1 (2x + m) passe pelo ponto (−2, 1). 3 3. (IBMEC-2001) Na figura abaixo, est˜o representadas as fun¸˜es reais: a co 2 f (x) = ax + 2 e g(x) = − x + b 3 y f g B A C x 0 Sabendo que AC × 0B = 8 ent˜o, a reta que representa a fun¸˜o f a ca passa pelo ponto: a) (1.3) b) (−2, −2) c) (−1, 4) d) (2,4) e) (3,6) CEDERJ 176
- 179. o Fun¸˜o do 1¯ grau ca ´ MODULO 1 - AULA 15 4. Determine f (x) cujos gr´ficos s˜o representados abaixo: a a y y 5 x 6 -3 3 x y y 12 45º x 60º -10 x 5. Resolver as inequa¸˜es do 1o grau: co ¯ a) 4x + 40 > 0 b) 12 − 6x ≥ 0 c) 2x + 3 < 13 d) x + 1 < 2x e) 1 + 2x < 1 − 2x f) 2(x − 1) ≥ 1 − 3(1 − x) 2x − 3 6. (UERJ 93) O conjunto solu¸˜o da inequa¸˜o ca ca ≥ 1 ´ o seguinte e 3x − 2 intervalo: 2 2 2 a) (−∞, −1) b) −∞, c) −1, d) [−1, ∞) e) ,1 3 3 3 7. (CESGRANRIO) O conjunto de todos os n´ meros reais x < 1 que u 2 satisfazem a inequa¸˜o ca < 1 ´: e x−1 a) {0} b) {0, 1/2} c) {x ∈ R | −1 < x < 1} d) {x ∈ R | x < 0} e) {x ∈ R | x < 1} 177 CEDERJ
- 180. o Fun¸˜o do 1¯ grau ca 8. (FUVEST-SP) A fun¸˜o que representa o valor a ser pago ap´s um ca o desconto de 3% sobre o valor x de uma mercadoria ´: e a) f (x) = x − 3 b) f (x) = 0, 97x c) f (x) = 1, 3x d) f (x) = −3x e) f (x) = 1, 03x 9. (CESGRANRIO) Os valores positivos de x, para os quais (x − 1) · (x − 2) · (x − 3) > 0, constituem o intervalo aberto: a) (1,3) b) (2,3) c) (0,3) d) (0,1) e) (1,2) 10. (UFSC) Seja f (x) = ax + b uma fun¸˜o afim. Sabe-se que f (−1) = 4 ca e f (2) = 7. O valor de f (8) ´: e a) 0 b) 3 c) 13 d) 23 e) 33 11. (UFF 93) y 6 -2 x A soma do coeficiente angular com o coeficiente linear da reta repre- sentada no gr´fico acima ´: a e a) −3 b) −3 c) 3 d) 4 e) 9 x−3 x−1 12. (PUC 91) A raiz da equa¸˜o ca = ´: e 7 4 a) −5/3 b) −3/5 c) 5/3 d) 3/5 e) 2/5 13. (UNIFOR/CE) Seja a fun¸˜o f de R em R, definida por f (x) = 3x − 2. ca A raiz da equa¸˜o f (f (x)) = 0 ´: ca e 1 1 8 8 a) x ≤ 0 b) 0 < x ≤ c) <x≤1 d) 1 < x < e) x > 3 3 3 3 14. (PUC-RJ) Uma encomenda, para ser enviada pelo correio, tem um custo C de 10 reais para um peso P de at´ 1 kg. Para cada quilo e adicional o custo aumenta 30 centavos. A fun¸˜o que representa o ca custo de uma encomenda de peso P ≥ 1 kg ´: e a) C = 10 + 3P b) C = 10P + 0, 3 c) C = 10 + 0, 3(P − 1) d) C = 9 + 3P e) C = 10P − 7 CEDERJ 178
- 181. o Fun¸˜o do 1¯ grau ca ´ MODULO 1 - AULA 15 15. (PUC) Em uma certa cidade, os tax´ ımetros marcam, nos percursos sem parada, uma quantia inicial de 4 UT (Unidade Taxim´trica) e mais 0,2 e UT por quilˆmetro rodado. Se, ao final de um percurso sem paradas, o o tax´ ımetro registrava 8,2 UT, o total de quilˆmetros percorridos foi: o a) 15,5 b) 21 c) 25,5 d) 27 e) 32,5 16. Seja a fun¸˜o f : R → R, tal que f (x) = ax + b. Se os pontos (0 − 3) e ca (2,0) pertencem ao gr´fico de f , ent˜o a + b ´ igual a: a a e a) 9/2 b) 3 c) 2/3 d) −3/2 e) −1 Exerc´ ıcios - S´rie B e 1. (UNICAMP-92) Calcule a e b positivos na equa¸˜o da reta ax + by = 6 ca de modo que ela passe pelo ponto (3,1) e forme com os eixos coorde- nados um triˆngulo de ´rea igual a 6. a a 2. (UFRJ-91) Suponha que as liga¸˜es telefˆnicas em uma cidade sejam co o apenas locais e que a tarifa telefˆnica seja cobrada do seguinte modo: o 1o ) uma parte fixa, que ´ assinatura; ¯ e 2o ) uma parte vari´vel, dependendo do n´ mero de pulsos que excede ¯ a u 90 pulsos mensais. Assim, uma pessoa que tem registrados 150 pulsos na conta mensal de seu telefone pagar´ somente 150 − 90 = a 60 pulsos, al´m da assinatura. e Em certo mˆs, o pre¸o de cada pulso excedente era R$ 2,00 e o da e c assinatura era R$ 125,00. Um usu´rio gastou nesse mˆs 220 pulsos. a e Qual o valor cobrado na conta telefˆnica? o 3. (UFRJ-95) Uma f´brica produz ´leo de soja sob encomenda, de modo a o que toda produ¸˜o ´ comercializada. ca e O custo de produ¸˜o ´ composto de duas parcelas. Uma parcela fixa, ca e independente do volume produzido, corresponde a gastos com aluguel, manuten¸˜o de equipamentos, sal´rios etc; a outra parcela ´ vari´vel, ca a e a dependente da quantidade de ´leo fabricado. o 179 CEDERJ
- 182. o Fun¸˜o do 1¯ grau ca No gr´fico abaixo, a reta r1 representa o custo de produ¸˜o e a reta a ca r2 descreve o faturamento da empresa, ambos em fun¸˜o do n´ mero ca u de litros comercializados. A escala ´ tal que uma unidade representa e R$ 1.000,00 (mil reais) no eixo das ordenadas e mil litros no eixo das abscissas. a) Determine, em reais, o custo correspondente ` parcela fixa. a b) Determine o volume m´ ınimo de ´leo a ser produzido para que a o empresa n˜o tenha preju´ a ızo. 4. Resolver as seguintes desigualdades: a) (x − 1)(2x + 1) < 2x(x − 3) x+1 x+2 b) + >0 2 3 t2 − 1 1 t c) − ≤ (t − 1) 2 4 2 5. (UFPI) Se m, n e p s˜o os n´ meros inteiros do dom´ a u ınio da fun¸˜o real ca 2 2 2 f (x) = (3 − 2x) · (2x + 3), ent˜o m + n + p ´ igual a: a e a) 2 b) 5 c) 6 d) 8 e) 9 6. (CESGRANRIO) Dada a inequa¸˜o (3x − 2)3 (x − 5)2 (2 − x) x > 0 ca tem-se que a solu¸˜o ´: ca e 2 a) z | x < ou 2 < x < 5 3 2 b) x | < x < 2 ou x < 0 3 c) 2/3 ≤ x ≤ 2 d) 2/3 < x < 5 e) diferente das quatro anteriores CEDERJ 180
- 183. o Fun¸˜o do 1¯ grau ca ´ MODULO 1 - AULA 15 1+x 7. (PUC-SP) O dom´ ınio da fun¸˜o real dada por f (x) = ca ´: e x−4 a) {x ∈ R | x > −1 e x < 4} b) {x ∈ R | x < −1 ou x > 4} c) {x ∈ R | x ≥ −1 e x ≥ 4} d) {x ∈ R | x ≤ −1 ou x > 4} e) n.r.a. 8. (UNICAMP) Duas torneiras s˜o abertas juntas; a 1a enchendo um a ¯ a tanque em 5 horas, a 2¯ enchendo outro tanque de igual volume em 4 horas. No fim de quanto tempo, a partir do momento em que as torneiras s˜o abertas, o volume que falta para encher o 2o tanque ´ 1/4 a ¯ e do volume que falta para encher o 1o tanque? ¯ 9. (ESPM/SP) Uma empresa de bicicletas possui um custo unit´rio de a produ¸˜o de US$ 28,00 e pretende que este valor represente 80% do ca pre¸o de venda ao lojista. Esta, por sua vez, deseja que o valor pago ao c fabricante seja apenas 70% do total que custar´ ao consumidor final. a Quanto o consumidor final dever´ pagar por uma bicicleta? a 2x − 3 10. (PUC/MG) Seja f : R → R uma fun¸˜o definida por f (x) = ca · 5 7 O valor de x na equa¸˜o f −1 (x) = ´: ca e 2 a) 3/8 b) 4/5 c) 2/7 d) −4/5 e) −3/8 Gabarito S´rie A e 1. a) a d´cada de 40 b) 2040 < A < 2050 2. m = 7 3. b) e 3 √ 4. a) f (x) = y = x − 3 b) y = −2x + 6 c) y = 3x + 12 d) 5 y = −x − 10 5. a) S = {x ∈ R | x > −10} = (−10, ∞) b) {x ∈ R | x ≤ 2} =) − ∞, 2] c) {x ∈ R | x < 5} = (−∞, 5) d) {x ∈ R | x > 1} = (1, ∞) e) {x ∈ R | x < 0} = (−∞, 0) f) {x ∈ R | x ≤ 0} = (−∞, 0] 6. c) 7. e) 8. b) 9. e) 10. c) 11. e) 12. a) 13. c) 14. c) 15. b) 16. d) 181 CEDERJ
- 184. o Fun¸˜o do 1¯ grau ca S´rie B e 1. a = 1, b = 3 2. a = R$ 385,00 3. a) R$ 10.000,00 b) 10000 litros 1 1 7 7 4. a) x ∈ R | x < = −∞, k b) x ∈ R | x > − = − ,∞ 5 5 5 5 3 3 c) t ∈ R | t ≤ = −∞, 5. a) 6. b) 7. d) 8. 3h45min 2 2 9. US$50,00 10. b) Auto-avalia¸˜o ca Antes de passar ` aula seguinte, vocˆ deve resolver todos os exerc´ a e ıcios da S´rie A. A S´rie B fica como exerc´ de aprofundamento. e e ıcio CEDERJ 182
- 185. Fun¸˜o quadr´tica ca a ´ MODULO 1 - AULA 16 Aula 16 – Fun¸˜o quadr´tica ca a Objetivos: Ap´s estudar esta aula, vocˆ saber´: o e a • Reconhecer uma fun¸˜o quadr´tica, bem como representar seu gr´fico ca a a num sistema de coordenadas. • Determinar as ra´ de uma fun¸˜o quadr´tica e seus pontos de m´ximo ızes ca a a ou de m´ ınimo. • Descrever para uma dada fun¸˜o quadr´tica os intervalos do dom´ ca a ınio onde a fun¸˜o ´ positiva ou ´ negativa. ca e e Defini¸˜o ca Dados os n´ meros reais a, b e c (com a = 0), a fun¸˜o u ca 2 f : R → R, x → y = ax + bx + c ´ chamada fun¸˜o quadr´tica ou fun¸˜o polinomial de grau dois. e ca a ca Gr´fico no sistema cartesiano a Toda fun¸˜o quadr´tica ´ representada graficamente por uma par´bola. ca a e a Temos duas observa¸˜es importantes: co (i) As par´bolas que s˜o gr´ficos de fun¸˜es quadr´ticas tˆm eixo paralelo a a a co a e ao eixo vertical Oy (ii) Se a > 0 a concavidade da par´bola ´ para cima. Se a < 0 a concavi- a e dade ´ para baixo. e Exemplos Abaixo temos os gr´ficos de f (x) = x2 − 2x + 1, a g(x) = −x2 + x, respectivamente. y y a<0 a>0 0 1 x 1 x 183 CEDERJ
- 186. Fun¸˜o quadr´tica ca a Interse¸˜o com os eixos coordenados ca −→ (I) Interse¸˜o com Ox. ca Os gr´ficos anteriores mostram exemplos de gr´ficos, onde as par´bolas a a a −→ interceptam, uma ou duas vezes o eixo Ox. No caso de apenas um ponto de −→ interse¸˜o a par´bola ´ tangente ao eixo Ox. ca a e −→ Para encontrar genericamente os pontos de interse¸˜o com Ox fazemos ca 2 ax + bx + c = 0. As solu¸˜es desta opera¸˜o s˜o co ca a √ −b ± ∆ x= , ∆ = b2 − 4ac (*) 2a a) Se ∆ > 0 ⇒ temos duas ra´ x1 e x2 distintas em (*) ⇒ o gr´fico corta ızes a −→ o eixo Ox nestes pontos. x1 x2 x1 x2 x x a>0 a<0 b) Se ∆ = 0 ⇒ temos apenas uma raiz x0 em (*) ⇒ o gr´fico tangencia o a −→ eixo Ox. x0 x0 x x a>0 a<0 c) Se ∆ < 0 ⇒ n˜o existe solu¸˜o para (*). Neste caso a par´bola n˜o corta a ca a a −→ o eixo Ox. x1 x2 x1 x2 x x a>0 a<0 −→ II) Interse¸˜o com o eixo Oy ca Fazendo x = 0, temos que y = a · 02 + b · 0 + c. Logo y = c. Portanto, (0, c) ´ o ponto de interse¸˜o com o eixo y. e ca Exemplos: Determine o valor de m para que a fun¸˜o quadr´tica ca a f (x) = x2 − 4x + m possua apenas uma raiz. Solu¸˜o: Devemos ter ∆ = b2 − 4ac = 0. ca 42 − 4 · 1 · m = 0 ⇔ 4 − 4m = 0, m = 1. CEDERJ 184
- 187. Fun¸˜o quadr´tica ca a ´ MODULO 1 - AULA 16 Determina¸˜o das ra´ ca ızes √ −b ± ∆ Para ax2 + bx + c = 0, x = . 2a Ou seja √ √ −b + ∆ −b − ∆ x1 = e x2 = , 2a 2a s˜o as ra´ a ızes. (I) Soma e produto das ra´ ızes √ √ −b + ∆ −b − ∆ x1 + x2 = + = 2a 2a −b b b = − =− 2a √ 2a a √ −b + ∆ −b − ∆ x1 · x2 = · = 2a √ 2a √ (−b + ∆)(−b − ∆) = = 4a2 b2 − ∆ b2 − (b2 − 4ac) = = = 4a2 4a2 4ac c = 2 = 4a a b c x1 + x2 = − , x1 · x2 = a a Nota: Se f (x) = y = ax2 + bx + c b c y = a x2 + x+ . a a Ent˜o chamando de S a soma das ra´ e de P o produto das ra´ a ızes ızes, encon- tramos y = a(x2 − Sx + P ). (II) Fatora¸˜o da fun¸˜o quadr´tica ca ca a Afirmamos que y = f (x) = ax2 + bx + c = a(x − x1 )(x − x2 ). De fato, a(x − x1 )(x − x2 ) = a(x2 − x1 x − x2 x + x1 x2 ) = a[x2 − (x1 + x2 )x + x1 x2 ] = b c a x2 + x+ = ax2 + bx + c a a 185 CEDERJ
- 188. Fun¸˜o quadr´tica ca a (III) Pontos de m´ximo (a < 0) ou de m´ a ınimo (a > 0) para uma fun¸˜o ca quadr´tica. a Vamos denotar por (xv , yv ) as coordenadas do ponto m´ximo (a > 0) a ou ponto m´ ınimo (a < 0) da par´bola. a (a) Identifica¸˜o coordenada xv . ca Devido ` simetria da par´bola, no caso em que ∆ ≥ 0, o ponto m´dio a a e xv do segmento cujos extremos s˜o os pontos x1 e x2 (ra´ a ızes da equa¸˜o) ´ ca e x1 + x2 onde ocorre o valor m´ ınimo da fun¸˜o. Como xv = ca , encontramos 2 b b que xv = − . No caso em que ∆ < 0, ´ poss´ ainda provar que xv = − e ıvel 2a a ´ ainda o ponto onde ocorre o m´ximo ou m´ e a ınimo. Portanto, neste ponto ocorre o valor yv m´ınimo para y (caso a > 0) e o valor yv m´ximo para y a (caso a < 0). Veja abaixo, os gr´ficos das duas situa¸˜es. a co xv = b 2a b yv xv = 2a yv Nota: Conforme dito, quando ∆ ≥ 0, o valor xv que fornece o m´ ınimo repre- senta a m´dia aritm´tica das ra´ x1 e x2 , e e ızes x1 + x2 −b xv = = · 2 2a (b) C´lculo de yv a O ponto V = (xv , yv ) identifica o v´rtice da par´bola, e a y Eixo da parábola xv x yv v 2 −b −b yv = ax2 + bxv + c = a v +b +c 2a 2a b2 b2 b2 − 2b2 + 4ac −b2 + 4ac = − +c= = 4a 2a 4a 4a −∆ yv = . 4a CEDERJ 186
- 189. Fun¸˜o quadr´tica ca a ´ MODULO 1 - AULA 16 c) Dom´ ınio e conjunto imagem ınio y = f (x) = ax2 + bx + c ´ toda a reta real R. O dom´ e O conjunto imagem depende do sinal do coeficiente a. o 1¯ caso: a > 0 y D v 4a −∆ Im(f ) = y ∈ R | y ≥ 4a o 2¯ caso: a < 0 y D v 4a −∆ Im(f ) = y ∈ R | y ≤ 4a Exemplos 1. Determinar as ra´ da fun¸˜o definida pela equa¸˜o y = x2 − 2x − 8 ızes ca ca e fazer um esbo¸o do gr´fico. c a Solu¸˜o: ca x2 − 2x − 8 = 0 ∆ = b2 − 4ac ∆ = (−2)2 − 4(1) · (−8) = 4 + 32 = 36 √ −b ± ∆ x= 2a √ √ (−2) + 36 2+6 (−2) − 36 2−6 x1 = = = 4 e x2 = = = −2 2·1 2 2·1 2 Gr´fico da Par´bola a a a = 1 > 0 ⇒ concavidade voltada para cima ∆ = 36 > 0 ⇒ a par´bola intercepta o eixo x em dois pontos. a y -2 4 x 187 CEDERJ
- 190. Fun¸˜o quadr´tica ca a 2. Determinar as ra´ da fun¸˜o definida pela equa¸˜o y = −x2 + x − 4 ızes ca ca e fazer um esbo¸o do gr´fico. c a Solu¸˜o: −x2 + x − 4 = 0 ca x2 − x + 4 = 0 ∆ = (−1)2 − 4(1) · (4) = 1 − 16 = −15, ∆ < 0 (n˜o tem ra´ reais). a ızes Gr´fico da Par´bola a a a = −1 < 0 ⇒ concavidade voltada para baixo ∆ = −15 < 0 ⇒ n˜o intercepta o eixo x a x 3. Dada a equa¸˜o y = x2 − x − 6, determinar o v´rtice da par´bola e ca e a constuir o seu gr´fico. a Solu¸˜o: y = x2 − x − 6 ca x2 − x − 6 = 0 ∆ = 1 + 24 = 25 √ 1 + 25 1+5 x1 = = =3 2 ·√1 2 1 − 25 1−5 x2 = = = −2 2·1 2 Ra´ızes: 3 e − 2 −b −∆ 1 −25 V = , = , 2a 4a 2 4 Gr´fico da Par´bola a a a = 1 ⇒ a > 0 ⇒ concavidade para cima −→ ∆ = 26 ⇒ ∆ > 0 ⇒ intercepta o eixo Ox em dois pontos y -2 3 x 1 ( 2 , -25 ) 4 CEDERJ 188
- 191. Fun¸˜o quadr´tica ca a ´ MODULO 1 - AULA 16 Estudo do sinal da fun¸˜o quadr´tica ca a No estudo do sinal da fun¸˜o y = ax2 +bx+c, temos 6 casos a considerar. ca Caso 1: ∆<0ea>0 Caso 2: ∆ < 0 e a < 0 −→ Os gr´ficos das par´bolas nestes casos n˜o interceptam o eixo Ox. a a a Ent˜o y > 0 no caso 1 e y < 0 no caso 2. a y y x x Caso 3: ∆ > 0 e a > 0 Caso 4: ∆ > 0 e a < 0 −→ Os gr´ficos das par´bolas nestes casos interceptam o eixo Ox em dois a a pontos (as ra´ x1 e x2 ) ızes y y x x1 x2 + x1 x2 + + x y ´ positivo para e y ´ positivo para e x ∈ (∞, x1 ) ∪ (x2 , ∞) x ∈ (x1 , x2 ) y ´ negativo para e y ´ negativo para e x ∈ (x1 , x2 ) x ∈ (−∞, x1 ) ∪ (x2 , ∞) Caso 5: ∆ = 0, a > 0 Caso 6: ∆ = 0, a < 0 x1 = x2 x1 = x2 Ent˜o y ´ positivo para todo x = x1 no caso 5 e y ´ negativo para todo a e e x = x1 no caso 6. 189 CEDERJ
- 192. Fun¸˜o quadr´tica ca a Regra s´ ıntese para quest˜o do sinal a (i) Se ∆ < 0 o sinal de y ´ o mesmo de a e (ii) Se ∆ = 0 o sinal de y ´ o mesmo de a (exceto para x = x1 = x2 quando e y = 0) (iii) Se ∆ > 0. mesmo de a contr´ rio de a a mesmo de a x1 x2 x O sinal de y nos intervalos (∞, x1 ), (x1 , x2 ) e (x2 , ∞) obedecem ao esquema acima. Exemplos 1. Resolva o inequa¸˜o ca 5x2 − 3x − 2 > 0 Solu¸˜o: ca ∆ = b2 − 4ac ∆ = 9 − (4 · 5 · −2) ∆ = 49 > 0 √ −b ± ∆ x= 2a 3±7 −2 x= x1 = 1, x2 = 10 5 b 3 xv´rtice = − = e 2a 10 ∆ 49 yv´rtice = − = − e 4a 20 Conjunto solu¸˜o S ca 2 S= x ∈ R | x > 1 ou x < − 5 CEDERJ 190
- 193. Fun¸˜o quadr´tica ca a ´ MODULO 1 - AULA 16 2. Encontre o conjunto S ⊂ R onde para todo x ∈ S ⇒ y > 0, onde y = x2 − 4x + 4 Solu¸˜o: ca ∆ = (−4)2 − 4 · (4) · (1) ∆ = 16 − 16 = 0 ∆=0 −(−4) x= =2 2·1 y 2 x O conjunto solu¸˜o ´: ca e S = {x ∈ R | x = 2} Exerc´ ıcios - S´rie A e 1. Determinar m, de modo que a par´bola definida pela fun¸˜o: a ca a) f (x) = (−2m + 3)x2 + 3x − 2 tenha concavidade voltada para baixo b) y = (5 − 3m)x2 + 16 tenha concavidade voltada para cima 2. Determine a equa¸˜o quadr´tica cujo gr´fico ´: ca a a e y -1 0 3 x -5 3. Determine em cada caso os sinais de a, b, c e ∆. a) y b) y x x 4. (UFRJ/92) A figura abaixo ´ o gr´fico de um trinˆmio do segundo grau. e a o y 3 -1 2 5 x Determine o trinˆmio. o 191 CEDERJ
- 194. Fun¸˜o quadr´tica ca a 5. Resolver as seguintes inequa¸˜es: co a) x2 + 2x − 3 > 0 b) −4x2 + 11x − 6 ≤ 0 c) 9x2 − 6x + 1 > 0 d) x2 − 5 < 0 e) x(x + 4) > −4(x + 4) f) (x − 1)2 ≥ 3 − x 6. (PUC-90) O n´ mero de pontos de interse¸˜o da par´bola u ca a 2 y = −4x + 3x + 1 com a reta y = 5x − 2 ´: e a) 0 b) 1 c) 2 d) 3 e) 4 7. (UFF-95) Considere m, n e p n´ meros reais e as fun¸˜es reais f e g de u co 2 vari´vel real, definidas por f (x) = mx + nx + p e g(x) = mx + p. A a alternativa que melhor representa os gr´ficos de f e g ´: a e a) y b) y x x c) y d) y e) y x x x 8. (PUC-RIO/99) O n´ mero de pontos de intersec¸˜o das duas par´bolas u ca a 2 2 y = x e y = 2x − 1 ´: e a) 0 b) 1 c) 2 d) 3 e) 4 9. (VEST-RIO/93) O valor m´ınimo da fun¸˜o real f (x) = x2 + x + 1 ´: ca e a) −1 b) 0 c) 1/2 d) 2/3 e) 3/4 10. (UFF) Para que a curva representativa da equa¸˜o dada por ca 2 y = px − 4x + 2 tangencie o eixo dos x, o valor da constante p deve ser igual a: a) −6 b) −2 c) 0 d) 2 e) 6 CEDERJ 192
- 195. Fun¸˜o quadr´tica ca a ´ MODULO 1 - AULA 16 11. (UNIFICADO-93) O v´rtice da par´bola y = x2 + x ´ o ponto: e a e 1 1 1 3 a) (−1, 0) b) − , − c) (0,0) d) , e) (1,2) 2 4 2 4 12. (PUC-91) O m´ınimo valor da fun¸˜o f (x) = x2 −6x+10 ocorre quando ca x vale: 5 a) 6 b) −6 c) 3 d) −3 e) − 3 Exerc´ ıcios - S´rie B e 1. (FUVEST-SP) 1 1 a) Se x + = b, calcule x2 + 2 x x 2 5 1 b) Resolva a equa¸˜o x − 5x + 8 − + 2 = 0 ca x x 2. (UFF-95) Determine o dom´ ınio da fun¸˜o real f (x) definida por ca 900 f (x) = x − · x 3. (UERJ/97) Numa partida de futebol, no instante em que os raios sola- res incidiam perpendicularmente sobre o gramado, o jogador “Chor˜o”a chutou a bola em dire¸˜o ao gol, de 2,30 m de altura interna. A sombra ca da bola descreveu uma reta que cruzou a linha do gol. A bola descreveu uma par´bola e quando come¸ou a cair da altura m´xima de 9 metros, a c a sua sombra se encontrava a 16 metros da linha do gol. Ap´s o chute o de “Chor˜o”, nenhum jogador conseguiu tocar na bola em movimento. a A representa¸˜o gr´fica do lance em um plano cartesiano est´ sugerida ca a a na figura a seguir: y 9m x 16 m x2 A equa¸˜o da par´bola era do tipo: Y = − + C. O ponto onde a ca a 36 bola tocou o gramado pela primeira vez foi: a) na baliza b) atr´s do gol c) dentro do gol d) antes da linha do gol a 4. (UFF-90) Duas fun¸˜es f e g definidas por f (x) = x2 + ax + b e co g(x) = cx2 + 3x + d interceptam-se nos pontos (0, −2) e (1, 0). De- termine os valores de a, b, c, e d. 193 CEDERJ
- 196. Fun¸˜o quadr´tica ca a 4 4 2 5. (PUC-91) Se 1 − + 2 = 0, ent˜o vale: a x x x 1 1 a) b) c) 1 d) 2 e) −1 ou 2 2 4 6. (PUC-88) Um quadrado e um retˆngulo, cujo comprimento ´ o triplo da a e largura, s˜o constru´ a ıdos usando-se todo um arame de 28 cm. Determine as dimens˜es do quadrado e do retˆngulo de forma que a soma de suas o a ´reas seja a menor poss´ a ıvel. 7. (UFRJ-90) Resolva a inequa¸˜o: ca x4 − 9x2 + 8 < 0 Gabarito S´rie A e 3 5 5 1. a) m > , b < 2. y = (x2 − 2x − 3) 3. a) a < 0; b > 0; 2 3 4 1 c > 0; ∆ > 0. b) a > 0; b < 0; c > 0; ∆ > 0 4. y = − x2 + 3 4 5 3 x+ 5. a) {x ∈ R | x < −3 ou x > 1} b) x ∈ R | x ≤ ou x ≥ 2 3 3 4 1 c) x ∈ R | x = d) {x ∈ R | 0 < x < 5} e) {x ∈ R | x ≤ −1 ou x ≥ 2} 3 f) {x ∈ R | x = −4} 6. c) 7. e) 8. c) 9. e) 10. d) 11. b) 12. c) S´rie B e √ 3± 5 1. a) b2 −2 b) 1, 2. D(f ) = {x ∈ R | −30 ≤ x < 0 ou x ≥ 30} 2 3. c) 4. a = 1, b = −2; c = −1, d = −2 5. c) 6. lado quadrado = 3, √ retˆngulo: altura = 2, comprimento = 6 7. S = {x ∈ R | −2 2 < x < −1 a √ ou 1 < x < 2 2} Auto-avalia¸˜o ca Antes de passar ` aula seguinte, vocˆ deve resolver todos os exerc´ a e ıcios da S´rie A. A S´rie B fica como exerc´ de aprofundamento. e e ıcio CEDERJ 194
- 197. Fun¸˜o Modular ca ´ MODULO 1 - AULA 17 Aula 17 – Fun¸˜o Modular ca Objetivos: O objetivo desta aula ´ possibilitar que vocˆ: e e • Compreenda o conceito de m´dulo de um n´ mero real e o conceito de o u fun¸˜o modular. ca • Possa construir gr´fico de fun¸˜es modulares. a co • Possa resolver equa¸˜es e inequa¸˜es envolvendo m´dulos. co co o Introdu¸˜o ca O m´dulo de um n´ mero real x ´ definido por: o u e x se x ≥ 0 |x| = −x se x < 0 O m´dulo de x tamb´m ´ chamado de valor absoluto de x. o e e Exemplo 1 |3| = 3 |3, 15| = 3, 15 | − 1| = 1 | − 1| = 7 1 7 |0| = 0 √ Observa¸˜o. Para qualquer n´ mero real x vale sempre x2 = |x|. N˜o ´ ca u a e √ sempre verdade que x 2 = x, por exemplo (−12) ´ 2 = 12. E claro que √ x2 = x, se x ≥ 0. Fun¸˜o modular ca Chamamos de fun¸˜o modular qualquer fun¸˜o de vari´vel real x cuja ca ca a defini¸˜o envolva m´dulos da vari´vel. ca o a Exemplo 2. O exemplo mais simples de uma fun¸˜o envolvendo m´dulos ´ o ca o e da fun¸˜o f : R → R definida por: ca f (x) = |x|. 195 CEDERJ
- 198. Fun¸˜o Modular ca O gr´fico desta fun¸˜o ´ apresentada na figura a seguir. Observe que, a ca e como x se x ≥ 0 f (x) = |x| = , −x se x < 0 ent˜o o gr´fico de f ´ formado pela reta y = x na parte do dom´ da fun¸˜o a a e ınio ca onde x ≥ 0 e y = −x na parte do dom´ ınio da fun¸˜o onde x < 0. ca 0 Constru¸˜o de gr´ficos ca a Vamos considerar um caso um pouco mais geral, onde f (x) ´ uma e fun¸˜o definida por f (x) = |g(x)|. Para construir o gr´fico analisamos para ca a que intervalos de x, vale g(x) ≥ 0 e para que intervalos de x, g(x) < 0. Isto ´, fazemos o estudo de sinais da fun¸˜o g(x) sobre a qual atua o m´dulo. e ca o Naturalmente, vale que f (x) = |g(x)| = g(x) se g(x) ≥ 0 e f (x) = |g(x)| = −g(x) se g(x) < 0. Vamos a alguns exemplos. Exemplo 3 Esboce o gr´fico de f (x) = |4 − x2 |. a Solu¸˜o: ca Fazemos o estudo de sinais de 4 − x2 . Esta ´ uma fun¸˜o quadr´tica, e ca a com ra´ızes ±2, cujo gr´fico ´ uma par´bola com concavidade voltada para a e a baixo. O gr´fico de 4 − x2 ´ a e 0 CEDERJ 196
- 199. Fun¸˜o Modular ca ´ MODULO 1 - AULA 17 O gr´fico de f (x) = |4 − x2 | ser´ a a 0 Note que para −2 ≤ x ≤ 2 temos que x2 −4 ≥ 0. Portanto, o gr´fico de a 2 f (x) coincide com o gr´fico de x − 4. No entanto, para os valores x < −2 e a 2 x > 2 temos que x − 4 < 0. Logo o gr´fico de f (x) ´ o sim´trico, em rela¸˜o a e e ca 2 ao eixo Ox, do gr´fico de x − 4. a Exemplo 4 f (x) = |x − 2| + |x + 1| Solu¸˜o: ca Neste caso ´ necess´rio separar o dom´ em v´rios intervalos. Temos: e a ınio a x−2 se x ≥ 2 |x − 2| = e −(x − 2) = 2 − x se x < 2 x+1 se x ≥ −1 |x + 1| = . −(x + 1) = −x − 1 se x < −1 Intervalos a serem considerados: 2-x 2-x x-2 |x-2| -1 2 -x-1 x+1 x+1 |x+1| -1 2 Portanto, (2 − x) + (−x − 1) = 1 − 2x se x < −1 f (x) = |x − 2| + |x + 1| = 2 − x + (x + 1) = 3 se − 1 ≤ x < 2 x − 2 + x + 1 = 2x − 1 se x ≥ 2 Cujo gr´fico ´ : a e 0 197 CEDERJ
- 200. Fun¸˜o Modular ca Equa¸˜es e inequa¸˜es modulares co co Uma equa¸˜o modular ´ simplesmente uma equa¸˜o que envolve fun¸˜es ca e ca co modulares (o mesmo para inequa¸˜es). co A seguir vamos listar algumas propriedades simples, no entanto muito uteis, para resolver equa¸˜es e inequa¸˜es modulares: ´ co co 1. |x| ≥ 0 para todo x ∈ R. Portanto n˜o existe n´ mero real x para o a u qual |x| < 0. 2. Se a > 0 ent˜o a |x| = a ⇔ x = a ou x = −a . 3. |x| = 0 ⇔ x = 0. 4. Se |a| > 0 ent˜o a |x| < a ⇒ −a < x < a . 5. |x| = |y| ⇔ x = y ou x = −y. Exemplo 5 1. Resolva a equa¸˜o |x2 − 4x| = 4 ca Solu¸˜o: (Veja a propriedade 2) ca |x2 − 4x| = 4 ⇒ x2 − 4x = 4 ou x2 − 4x = −4 √ 4 ± 32 √ x2 − 4x = 4 ⇒ x2 − 4x − 4 = 0 ⇒ x = =2±2 2 2 2 2 x − 4x = −4 ⇒ x − 4x + 4 = 0 ⇒ x = 2 Portanto a o conjunto solu¸˜o S da equa¸˜o ´ o conjunto: ca ca e √ √ S = {2 + 2, 2 − 2, 2} 2. Resolva a equa¸˜o |2x + 3| = |x − 4| ca Solu¸˜o: (Veja a propriedade 6) ca |2x + 3| = |x − 4| ⇒ 2x + 3 = x − 4 ou 2x + 3 = −(x − 4) 2x + 3 = x − 4 ⇒ x = −7 7 2x + 3 = −(x − 4) ⇒ 3x = −7 ⇒ x = − 3 O conjunto solu¸˜o S da equa¸˜o ´ o conjunto: ca ca e 7 S = {−7, − }. 3 CEDERJ 198
- 201. Fun¸˜o Modular ca ´ MODULO 1 - AULA 17 3. Resolva a inequa¸˜o |2x − 1| ≤ 4 ca Solu¸˜o: (Veja a propriedade 5) ca |2x − 1| ≤ 4 ⇒ −4 ≤ 2x − 1 ≤ 4 3 −4 ≤ 2x − 1 ⇒ − 2 ≤ x 5 2x + 3 ≤ 4 ⇒ x ≤ 2 O conjunto solu¸˜o S da inequa¸˜o ´ o conjunto: ca ca e 3 5 S= − , . 2 2 4. Resolva a inequa¸˜o |x2 − 4| ≥ 4 ca Solu¸˜o: (Veja a propriedade 4) ca |x2 − 4| ≥ 4 ⇒ x2 − 4 ≥ 4 ou x2 − 4 ≤ −4 √ √ √ x2 − 4 ≥ 4 ⇒ x2 ≥ 8 ⇒ x ≥ 8 = 2 2 ou x ≤ −2 2 x2 − 4 ≤ −4 ⇒ x2 ≤ 0 ⇒ x = 0 Portanto o conjunto solu¸˜o S ´ composto de todos os valores x tais ca e √ √ que x = 0 ou x ≤ −2 2 ou x ≥ 2 2. √ √ Ent˜o a S = {0} ∪ (−∞, −2 2] ∪ [2 2, ∞). Exerc´ ıcios - S´rie A e 1. O gr´fico que melhor representa a fun¸˜o f (x) = |x + 1| − |x − 1| ´: a ca e a) b) y c) y y -1 1 2 x 2 -1 1 x -2 -1 1 x -2 d) y e) 2 y 2 -1 1 x -2 -1 1 2 x -2 2. (Uni-Rio - 99) Sejam as fun¸˜es co f :R → R g:R → R e x → y = |x| x → x2 − 2x − 8 Fa¸a um esbo¸o do gr´fico da fun¸˜o f og. c c a ca 199 CEDERJ
- 202. Fun¸˜o Modular ca 3. (UFRJ - 99) Durante o ano de 1997 uma empresa teve seu lucro di´rio a L dado pela fun¸˜o ca L(x) = 50(|x − 100| + |x − 200|) onde x = 1, 2, ..., 365 corresponde a cada dia do ano e L ´ dado em e reais. Determine em que dias (x) do ano o lucro foi de R$ 10.000, 00. 4. (FUVEST) Determine as ra´ das seguintes equa¸˜es: ızes co a) |2x − 3| = 5 b) |2x2 − 1| + x = 0 5. (Osec-SP) O conjunto solu¸˜o da inequa¸˜o |x + 1| > 3 ´ o conjunto ca ca e dos n´ meros reais x tais que: u a) 2 < x < 4 b) x < −4 ou x > 2 c) x ≤ −4 ou x > 2 d) x < −4 e x > 2 e) x > 2 6. (MACKENZIE-SP) A solu¸˜o da inequa¸˜o |x| ≤ −1 ´ dada pelo con- ca ca e junto: a) ∅ b) ] − 1; 1[ c) [−1; ∞[ d) [−1; 1] e) ] − ∞; −1] 7. (PUC/CAMPINAS-SP) Na figura abaixo tem-se o gr´fico da fun¸˜o f, a ca de R em R, definida por: a) f(x)=|x + 1| b) f(x)=|x − 1| c) f(x)=|x| − 1 1 d) f(x)=|x2 − 1| e) f(x)=|1 − x| 1 8. (UECE) Sejam Z o conjunto dos n´ meros inteiros, S = {x ∈ Z; u 2 x − 3x + 2 = 0} e T = {x ∈ Z; |x − 1| < 3}. O n´ mero de ele- u mentos do conjunto T − S ´: e a) 1 b) 2 c) 3 d) 4 e) 5 9. (Cesgranrio) A soma das solu¸˜es reais de |x + 2| = 2|x − 2| ´: co e 1 2 19 20 a) b) c) 6 d) e) 3 3 3 3 10. (CESGRANRIO) Trace o gr´fico da fun¸˜o f de R em R, definida por a ca f (x) = (x2 − 1) + |x2 − 1| + 1. CEDERJ 200
- 203. Fun¸˜o Modular ca ´ MODULO 1 - AULA 17 Exerc´ ıcios - S´rie B e 1. (UNIFICADO - 97) O gr´fico que melhor representa a fun¸˜o real de- a ca √ finida por f (x) = x2 − 2x + 1 ´: e a) b) c) 1 1 1 -1 1 d) e) 1 1 -1 1 2. (UNIFICADO - 96) O gr´fico que melhor representa a fun¸˜o real de- a ca finida por f (x) = (x − 1) 2 + 1 ´: e a) y b) c) y y 1 1 1 1 x 1 x 1 x d) y e) 1 1 1 x 1 3. (PUC - 96) Sendo a > 0, o conjunto dos reais x tais que |a − 2x| < a ´: e a a) 2 b) o intervalo aberto (0, a) −a 3a c) o intervalo aberto , 2 2 a d) o intervalo aberto ,a 2 e) vazio 201 CEDERJ
- 204. Fun¸˜o Modular ca 4. (UFMG) Se f (x) = |x| + 1 e g(x) = −x2 + 6x − 10 para todo x real, ent˜o pode-se afirmar que f (g(x)) ´ igual a: a e a) x2 + 6x − 11 b)x2 + 6x − 9 c) x2 − 6x + 11 d) x2 − 6x + 9 e) x2 − 6x − 11 5. (UFF - 99) Considere o sistema y > |x| y≤ 2 A regi˜o do plano que melhor representa a solu¸˜o ´: a ca e y y a) b) y c) 2 2 2 0 x 0 x 0 x y y d) e) 2 2 0 x 0 x 1 6. (FEI-SP) A solu¸˜o da inequa¸˜o ca ca < 1 ´: e |1 − 2x| a) 0 < x < 1 b) x < −1 ou x > 0 c) −1 < x < 0 d) x < 0 ou x > 1 e) x < −1 ou x > 1 7. (F.C. Chagas-BA) O maior valor assumido pela fun¸˜o y = 2−|x−2| ´: ca e a) 1 b) 2 c) 3 d) 4 e) ∞ 8. (CESGRANRIO) Seja a fun¸˜o definida no intervalo aberto ] − 1, 1[ ca x −1 por f (x) = . Ent˜o, f a vale: 1 − |x| 2 1 1 −1 a) b) c) d) −1 e) −2 2 4 2 CEDERJ 202
- 205. Fun¸˜o Modular ca ´ MODULO 1 - AULA 17 9. (UNI-RIO) Sendo R = {(x, y) ∈ R2 | |x| ≤ 1 e |y| ≤ 1} a representa¸˜o ca gr´fica de R num plano cartesiano ´: a e a) uma reta b) um triˆngulo a c) um quadrado d) um losango e) uma circunferˆncia e 10. (UNI-RIO-92) A representa¸˜o gr´fica da fun¸˜o y = |x2 − |x|| ´: ca a ca e a) b) c) 1 1 -1 0 1 -1 0 1 -1 0 1 d) e) -1 0 1 0 |x| |x − 1| 11. (U.MACK) O conjunto solu¸˜o da equa¸˜o ca ca = ´: e x x−1 a) R − {0, 1} b) {x ∈ R | x > 1 ou x < 0} c) {x ∈ R | 0 < x < 1} d) ∅ e) nenhuma das alternativas anteriores ´ correta. e 203 CEDERJ
- 206. Fun¸˜o Modular ca Gabarito S´rie A e 1) c) 2) y 9 8 -2 1 4 x -9 3) x = 50 ou x = 250 4) a) x = −1 e x = 4 b) x = − 1 e x = −1 2 5) b) 6) a) 7) e) 8) c) 9) e) 10) y -1 1 x S´rie B e 1) e) 2) c) 3) b) 4) c) 5) b) 6) d) 7) b) 8) d) 9) c) 10) c) 11) b) ¸˜ AUTO-AVALIACAO Antes de passar ` aula seguinte, vocˆ deve resolver todos os exerc´ a e ıcios da S´rie A. A S´rie B fica como exerc´ de aprofundamento. e e ıcio CEDERJ 204
- 207. Fun¸˜o Exponencial ca ´ MODULO 1 - AULA 18 Aula 18 – Fun¸˜o Exponencial ca Objetivos: Ao final desta aula, vocˆ dever´ ser capaz de: e a • Entender o conceito de fun¸˜o exponencial e expressar gr´ficos destas ca a fun¸˜es. co • Resolver equa¸˜es exponenciais. co Defini¸˜o ca Uma fun¸˜o exponencial ´ uma fun¸˜o f : R → R definida por f (x) = ax , ca e ca onde a ´ um n´ mero real fixo, a > 0 e a = 1. e u Vamos fazer duas observa¸˜es sobre a defini¸˜o de fun¸ao exponencial: co ca c˜ a) Dom(f ) = R, pois, para todo x ∈ R, ax ´ um n´ mero real bem e u definido. Devemos comentar o que foi dito neste item a). Sabemos calcular an , se n ´ um n´ mero natural. Neste caso, an = a · a · . . . · a (n vezes). Se n ´ e u e −n 1 um n´ mero inteiro negativo e a = 0 ent˜o an = u a . Para os casos de a expoentes racionais, usamos ra´ en´simas compostas com exponencia¸˜o. ızes e ca m √ m Por exemplo, a n = am . Note que dado um n´ mero racional , podemos n u n considerar que n > 0 (do contr´rio multiplicar´ a ıamos numerador e denomi- nador por −1). Ent˜o sabemos calcular aq onde q ´ n´ mero racional. Para a e u o c´lculo de ax , onde x ´ real, devemos usar a t´cnica de aproxima¸˜o por a e e ca limite. Tomamos uma seq¨ˆncia de n´ meros racionais qn convergindo para ue u x qn x e ent˜o a ´ o limite de a . No entanto, o assunto limite, nestes termos, ´ a e e avan¸ado em rela¸˜o ao n´ que estamos trabalhando e pedimos para vocˆ c ca ıvel e aceitar sem provas a argumenta¸˜o que desenvolvemos. ca b) Im(f ) = (0, ∞), pois ax > 0, para todo x ∈ R. Gr´fico a Como f (0) = a0 = 1, o gr´fico da fun¸˜o sempre passa pelo ponto a ca (0, 1). Devemos distinguir 2 casos, de acordo com os valores de a. 205 CEDERJ
- 208. Fun¸˜o Exponencial ca Se a > 1 ent˜o a f (x) = ax ´ uma fun¸˜o crescente. a e ca y x y=a a >1 1 x Se 0 < a < 1 ent˜o f (x) = ax ´ uma fun¸˜o decrescente. a e ca y x y=a 0<a<1 1 x Exerc´ ıcios resolvidos 1. Esboce os gr´ficos das fun¸˜es y = 2x e y = e−3x . a co Solu¸˜o: ca x y=2 (0,1) 3x x 1 1 y = e−3x = = e e3 1 Como e ∼ 2.718 ent˜o 0 < = a < 1, portanto o gr´fico ´ do tipo a e e3 y -3 y=e 1 x CEDERJ 206
- 209. Fun¸˜o Exponencial ca ´ MODULO 1 - AULA 18 Equa¸˜es exponenciais co Uma equa¸˜o exponencial ´ uma equa¸˜o envolvendo potencia¸˜o, onde ca e ca ca a vari´vel pode aparecer na base e necessariamente aparecendo no expoente. a Vamos estudar apenas os casos mais simples destas equa¸˜es: co 1o Caso: f (x) e g(x) s˜o fun¸˜es, a ´ n´ mero real positivo diferente de 1 e a co e u af (x) = ag(x) ´ a equa¸˜o exponencial. Neste caso o conjunto solu¸˜o s˜o os valores x para e ca ca a os quais f (x) = g(x). Ent˜o, se a > 0, a af (x) = ag(x) ⇔ f (x) = g(x) . 2o Caso: f (x), g(x) e h(x) s˜o fun¸˜es, onde g(x) > 0, h(x) > 0, g(x) = 1 e a co h(x) = 1, para todo x e g(x)f (x) = h(x)f (x) . Os valores x que resolvem a equa¸˜o s˜o aqueles que provocam a igualdade ca a g(x) = h(x). Isto ´, e g(x)f (x) = h(x)f (x) ⇔ g(x) = f (x) . Muitas equa¸˜es exponenciais podem ser reduzidas a uma das formas acima co ap´s alguma manipula¸˜o alg´brica. Vamos a alguns exemplos. o ca e Exerc´ ıcios resolvidos 1. Resolva a equa¸˜o 32x−2 · 92x−6 = 81. ca Solu¸˜o: Vamos colocar esta equa¸˜o na forma 3f (x) = 3g(x) . ca ca 32x−2 · 92x−6 = 81. 32x−2 · (32 )2x−6 = 34 32x−2 · 34x−12 = 34 3(2x−2)+(4x−12) = 34 36x−14 = 34 Ent˜o, 6x − 14 = 4 a Logo, x = 3. Solu¸˜o: ca x = 3. 207 CEDERJ
- 210. Fun¸˜o Exponencial ca 2. Resolva a equa¸˜o 4x − 3 · 2x − 4 = 0. ca Solu¸˜o: Vamos fazer a substitui¸˜o y = 2x e reduzir a uma equa¸˜o ca ca ca o do 2¯ grau. 4x − 3 · 2x − 4 = 0 (22 )x − 3 · 2x − 4 = 0 (2x )2 − 3 · 2x − 4 = 0. Substituindo y = 2x , vem que y2 − 3 · y − 4 = 0 √ 3 ± 9 + 16 y= . 2 Logo, y = −1 ou y = 4. Substituindo agora y = 2x , vem que, 2x = −1 n˜o tem solu¸˜o; a ca 2x = 4 ⇒ 2 x = 22 ⇒ x=2 Solu¸˜o: x = 2 ca 2 −4 3. Resolva a equa¸˜o xx ca = 1. Solu¸˜o: Como x ´ a base, e o segundo membro ´ 1, s´ tem sentido ca e e o procurar solu¸˜es com x > 0 e x2 − 1 = 0. Neste caso podemos escrever co 2 que x = 1. Comparando os expoentes. xx −4 = 1 = x0 ⇒ x2 − 4 = 0 0 ⇒ x = ±2 Solu¸˜o: ca x = ±2 4. Resolva 3x−1 + 3x+1 = 30. Solu¸˜o: Vamos isolar o termo 3x . ca 3x−1 + 3x+1 = 30 3x · 3−1 + 3x · 3 = 30 1 x · 3 + 3 · 3x = 30 3 1 3x · + 3 = 30 3 10 3x · = 30 3 3 3x = × 30 = 9 10 3x = 32 ⇒ x = 2 Solu¸˜o: x = 2 ca CEDERJ 208
- 211. Fun¸˜o Exponencial ca ´ MODULO 1 - AULA 18 Inequa¸˜es exponenciais co Para resolvermos uma inequa¸˜o exponencial devemos, em geral, reduzi- ca f (x) la a uma inequa¸˜o do tipo h(x) ca > h(x)g(x) , onde f (x) e h(x) s˜o fun¸˜es a co e, al´m disso, h(x) > 0 e h(x) = 1, para todo valor x. e A solu¸˜o ent˜o depende da base h(x): ca a 1) se h(x) > 1 ent˜o a f (x) g(x) h(x) > h(x) ⇒ f (x) > g(x) 2) se 0 < h(x) < 1 ent˜o a f (x) g(x) h(x) > h(x) ⇒ f (x) < g(x) Exerc´ ıcios resolvidos 1. Resolva a inequa¸˜o 2−x < 16. ca Solu¸˜o: ca 2−x < 16 x 1 < 24 2 x −4 1 1 < . 2 2 Como a base est´ entre 0 e 1, ent˜o, em rela¸˜o aos expoentes, a desi- a a ca gualdade deve ser invertida. Assim, x −4 1 1 < ⇒ x > −4 2 2 1 2. Resolva a inequa¸˜o 9x+ 2 − 4 · 3x + 1 ≤ 0. ca Solu¸˜o: Vamos fazer a substitui¸˜o 3x = y. ca ca 1 9x+ 2 − 4 · 3x + 1 ≤ 0 1 9x · 9 2 − 4 · 3x + 1 ≤ 0 (32 )x · 3 − 4 · 3x + 1 ≤ 0 3 · (3x )2 − 4 · 3x + 1 ≤ 0. Substituindo y = 3x , temos que 3y 2 − 4y + 1 ≤ 0 209 CEDERJ
- 212. Fun¸˜o Exponencial ca √ 2 16 − 12 4± A equa¸˜o 3y − 4y + 1 = 0 tem solu¸˜es y = ca co ⇒ y=1 6 1 1 ou y = · Logo, 3y 2 − 4y + 1 ≤ 0 ⇒ ≤ y ≤ 1. Portanto, devemos 3 3 resolver as inequa¸˜es. co 1 ≤ 3x ≤ 1 . 3 1 ≤ 3x ⇒ 3−1 ≤ 3x ⇒ −1 ≤ x 3 3x ≤ 1 ⇒ 3x ≤ 30 ⇒ x ≤ 0. O conjunto solu¸˜o da inequa¸˜o ´ o intervalo fechado [−1, 0]. ca ca e 3. Determine o dom´ ınio da fun¸˜o ca √ f (x) = 3x − 1 Solu¸˜o: Como s´ tem sentido ra´ ca o ızes quadradas de n´ meros positivos u x ou nulos, devemos ter 3 − 1 ≥ 0. Assim, 3x ≥ 1 ⇒ 3x ≥ 30 ⇒ x ≥ 0 Portanto, Dom(f ) = [0, ∞). Exerc´ ıcios - S´rie A e 1. (CESGRANRIO-RJ) O gr´fico que melhor representa a fun¸ao a c˜ 2x f (x) = e ´:e y a) b) c) y y 1 1 1 x x x y d) y e) 1 x x CEDERJ 210
- 213. Fun¸˜o Exponencial ca ´ MODULO 1 - AULA 18 2. (UNESP-93) Uma substˆncia se decomp˜e aproximadamente segundo a a o lei Q(t) = K2−0,5t , onde K ´ uma constante, t indica o tempo (em minu- e tos) e Q(t) indica a quantidade de substˆncia (em gramas) no instante t. a Considerando-se os dados desse processo de decomposi¸˜o mostrados ca no gr´fico, determine os valores de k e a. a 3. (UNESP-94) A figura mostra os gr´ficos de uma fun¸˜o exponencial a ca y = a e da reta que passa pelo ponto 0, 3 e tem inclina¸˜o 10 · Pelo x 5 ca 7 ponto C = 1 , 0 passou-se a perpendicular ao eixo x, que corta os 2 gr´ficos, respectivamente, em B e A. a y A (0, 5/3) B C x ½ Supondo-se que B esteja entre A e C, conforme mostra a figura, e que 8 a medida do segmento AB ´ dada por e , determine o valor de a. 21 4. Esboce os gr´ficos de y = 2x − 1 e y = x. Verifique se 2x − 1 = x possui a solu¸˜o. ca 5. (FUVEST-99) A equa¸˜o 2x = −3x + 2, com x real, ca a) n˜o tem solu¸˜o. a ca 2 b) tem uma unica solu¸˜o entre 0 e ´ ca · 3 2 c) tem uma unica solu¸˜o entre − ´ ca e 0. 3 d) tem duas solu¸˜es, sendo uma negativa e outra positiva. co e) tem mais de duas solu¸˜es. co 211 CEDERJ
- 214. Fun¸˜o Exponencial ca 6. (UFF 95) Em uma cidade, a popula¸˜o de pessoas ´ dada por ca e P (t) = P o2t e a popula¸˜o de ratos ´ dada por R(t) = Ro4t , sendo ca e o tempo medido em anos. Se em 1992 havia 112.000 pessoas e 7.000 ratos, em que ano o n´ mero de ratos ser´ igual ao de pessoas? u a 7. (UNI-RIO) O qu´druplo da solu¸˜o da equa¸˜o 54x+3 = 25 ´: a ca ca e 1 a) 1 b) −1 c) −16 d) 5 e) − 4 16 8. (UNI-RIO) O valor de x na equa¸˜o: 3x−1 + 2 · 3x+1 − 3x = ca ´: e 27 a) 2 b) 2/3 c) 1/2 d) −1/2 e) −2 9. (PUC) A raiz da equa¸˜o 22x − 15 · 2x − 16 = 0 ´: ca e a) 16 b) 12 c) 10 d) 8 e) 4 2 −7x+5 10. (CESGRANRIO) O n´ mero de ra´ reais de 32x u ızes = 1 ´: e a) 0 b) 1 c)2 d) 3 e) maior que 3 11. Determine o dom´ ınio das fun¸˜es reais: co √ a) f (x) = 2x2 −1 − 1 1 b) f (x) = x 4 − 2x x−3 1 1 12. (UNI-RIO-96) Assinale o conjunto-solu¸˜o da inequa¸˜o ca ca ≤ · 2 4 a) ] − ∞, 5] b) [4, +∞[ c) [5, +∞[ d) {x ∈ R | x ≤ −5} e) {x ∈ R | x ≥ −5} 2 +5x−3 13. (UNI-RIO-99) Seja uma fun¸˜o f definida por f (x) = 2x ca . Deter- mine os valores de x tais que f (x) seja menor do que 8. 14. (PUC-SP) O valor de x, x ∈ R, que ´ solu¸˜o da equa¸˜o 4x+2 = 8−x+3 , e ca ca ´: e 1 1 4 a) 0 b) c) d) 1 e) 5 2 3 CEDERJ 212
- 215. Fun¸˜o Exponencial ca ´ MODULO 1 - AULA 18 Exerc´ ıcios - S´rie B e 1. Esboce o gr´fico de cada fun¸˜o abaixo e determine o conjunto imagem a ca a) y = 3x − 1 b) y = |2x − 2| √ 2. (FESP SP) Se x 2 = 16x , ent˜o os valores de x s˜o: a a 1 1 1 1 1 1 1 a) 0 e b) e − c) e − d) e − e) 0 e 1 2 4 2 2 2 8 8 3. (UNI-RIO - 2000) O conjunto-solu¸˜o da inequa¸˜o x2x ≥ xx+3 , onde ca ca x > 0 e x = 1, ´: e a) ]0, 1[∪[3, +∞[ b) {x ∈ R | 0 < x < 1} c) [3, +∞[ d) R e) ∅ x(x+1) x+1 1 1 4. (FESP-SP) A solu¸˜o da inequa¸˜o ca ca ≥ ´: e 3 3 1 a) x ≤ 0 b) x ≥ 0 c) x ≤ −1 ou x ≥ 1 d) −1 ≤ x ≤ 1 e) x ≥ 3 5. (PUC-RS) A solu¸˜o da equa¸˜o 2x+1 − 23−x − 6 = 0 pertence ao ca ca intervalo: a) −1 ≤ x < 2 d) 2 < x ≤ 4 b) −1 < x ≤ 2 e) 3 ≤ x < 4 c) 2 < x < 4 6. (MACKENZIE-SP) O valor de m, m ∈ R, que satisfaz a equa¸˜o ca 10 (2m+2 )3 = 2 3 ´: e 8 4 8 a) − b) 6 c) − d) − e) −6 9 3 9 7. (FEI-SP) Para que valor real de x temos 8x − 8−x = 3 · (1 + 8−x ): 1 2 a) 4 b) c) 2 d)1 e) 2 3 8. (PUC-MG) Se 3x+1 + 3x−1 − 3x−2 = 87, ent˜o 2x − 1 ´ igual a: a e a) 5 b) 6 c) 7 d) 8 e) 9 9. (UECE) Se 64|x| − 2 · 8|x| + 1 = 0, ent˜o x2 ´ igual a: a e 1 1 a) 0 b) c) d) 1 e) 4 9 4 2x + 3y = 11 10. (CESGRANRIO) Se (x, y) ´ solu¸˜o do sistema e ca a 2x − 3y = 5 soma (x + y) ´ igual a: e a) 11 b) 3 d) 6 d) 4 e) 5 213 CEDERJ
- 216. Fun¸˜o Exponencial ca Gabarito S´rie A e 1) c) 2) K = 2048 a = 4 min 3) a = 4 4) y 1 1 x possui duas solu¸˜es: x = 0 e x = 1 co 5) b) 6) Em 1996 7) b) 8) e) 9) e) 10) c) 11) a) D(f ) = (−∞, −1] ∪ [1, ∞) b) D(f ) = R − {0} 12) c) 13) (−6, 1) 14) d) S´rie B e 1) a) y x b) y 2 1 x 2) c) 3) a) 4) d) 5) b) 6) a) 7) e) 8) a) 9) a) 10) d) Auto-avalia¸˜o ca Antes de passar ` aula seguinte, vocˆ deve resolver todos os exerc´ a e ıcios da S´rie A. A S´rie B fica como exerc´ de aprofundamento. e e ıcio CEDERJ 214
- 217. Fun¸˜o logaritmo ca ´ MODULO 1 - AULA 19 Aula 19 – Fun¸˜o logaritmo ca Ojetivos: Ao t´rmino desta aula, vocˆ: e e • Compreender´ o conceito de fun¸˜o logar´ a ca ıtmica como inversa da fun¸˜o ca exponencial. • Entender´ e ser´ capaz de provar as principais propriedades da fun¸˜o a a ca logaritmo. • Usar´ as propriedades da fun¸˜o logaritmo para resolver equa¸˜es e a ca co inequa¸˜es. co Introdu¸˜o ca N´s j´ estudamos na aula anterior a fun¸˜o exponencial. Lembre como o a ca foi a defini¸˜o. Tomamos um n´ mero real a, satisfazendo a > 0 e a = 1 e ca u definimos, f : R → R, f (x) = ax . Para a fun¸˜o exponencial temos os seguintes conjuntos para dom´ ca ınio ınio ou imagem, Dom(f ) = R e Im(f ) = (0, ∞) . e contradom´ Tamb´m a fun¸˜o exponencial ´ injetiva. Isto ´, se x1 = x2 ⇒ ax1 = ax2 . e ca e e Logo podemos pensar na fun¸˜o inversa de f (x) = ax , definida no dom´ ca ınio (0, ∞) = R+ . Note que este dom´ınio para a fun¸˜o inversa ´ a imagem ou ca e contradom´ınio da fun¸˜o exponencial. ca O objetivo desta aula ´ estudar o logaritmo como fun¸˜o inversa da e ca exponencial. Sejam a um n´ mero real positivo (a > 0) e y um n´ mero real tal que u u y > 0 e y = 1. Denominamos o logaritmo de y na base a como sendo o n´ mero real x tal que ax = y. Usamos a nota¸˜o u ca x = loga y , e lemos “x ´ o logaritmo de y na base a”. e Portanto, loga y = x ⇐⇒ ax = y. 215 CEDERJ
- 218. Fun¸˜o logaritmo ca Na express˜o loga y = x, a • a ´ a base do logaritmo, e • y ´ o logaritmando ou antilogaritmo e • x ´ o logaritmo. e Em resumo, a express˜o x = loga y define a fun¸˜o loga como uma a ca fun¸˜o da vari´vel y e inversa da fun¸˜o exponencial. Para se convencer disto, ca a ca veja o diagrama abaixo, onde a primeira fun¸˜o ´ a fun¸˜o exponencial, a ca e ca segunda, a fun¸˜o logaritmo e observe que a composi¸˜o das fun¸˜es resulta ca ca co na fun¸˜o identidade (come¸amos com x e terminamos com x). ca c exponencial logaritmo R −→ (0, ∞) −→ R x −→ ax = y y −→ loga y = x O diagrama anterior explicita tamb´m os dom´ e ınios e contradom´ ınios das fun¸˜es. co Nota: i) Fixada a base a (a > 0, a = 1), o dom´ ınio da fun¸˜o loga ´ o intervalo ca e (0, ∞). Ent˜o para todo y > 0 tem sentido escrever loga y. a ii) A imagem ou contradom´ ınio de loga ´ todo o conjunto R. e Veja alguns exemplos simples: a) log2 64 = 6, pois 26 = 64 b) log1 20 = 0, pois 200 = 1 c) log15 15 = 1, pois 151 = 15 1 1 d) log5 = −2, pois 5−2 = 25 25 CEDERJ 216
- 219. Fun¸˜o logaritmo ca ´ MODULO 1 - AULA 19 Gr´ficos da fun¸˜o logaritmo a ca A fun¸˜o logaritmo ´ a fun¸˜o inversa da fun¸˜o exponencial. Portanto, ca e ca ca a partir dos gr´ficos das fun¸˜o exponencial, veja o item 2 da aula anterior; a ca concluimos que: a) Gr´fico de y = loga x, se a > 1 (base > 1). a y 1 x b) Gr´fico de y = loga x, se 0 < a < 1 (base entre 0 e 1). a y 1 x ´ Nota: E importante revisar o m´todo que permite a constru¸˜o dos gr´ficos e ca a da fun¸˜o logaritmo. ca Como a fun¸˜o logar´ ca ıtmica y = loga x ´ a inversa da fun¸˜o exponen- e ca cial y = ax , podemos obter seu gr´fico a partir do gr´fico da exponencial. a a Basta usar o fato de que o gr´fico de uma fun¸˜o e sua inversa s˜o sim´tricos a ca a e o o em rela¸˜o ` reta y = x, que ´ a reta bissetriz do 1¯ e 2¯ quadrantes. Repre- ca a e sentando em um mesmo gr´fico as fun¸˜es logaritmo e exponencial, temos: a co I. base b > 1 y y=x x 1 y=b 1 x y = logbx 217 CEDERJ
- 220. Fun¸˜o logaritmo ca II. 0 < base b < 1 y x y=x y=b x y = logbx Nos dois casos, para a fun¸˜o f (x) = logb x, vale que Dom(f ) = R∗ = (0, ∞) ca + e Im(f ) = R. Propriedades imediatas a) logb 1 = 0, pois b0 = 1, qualquer que seja a base b. Portanto, o gr´fico a da fun¸˜o y = logb x sempre passa pelo ponto (1, 0). ca b) logb b = 1, pois b1 = b, para qualquer base b. c) logb bm = m, pois bm = bm . Exemplo: log5 125 = log5 53 = 3. Exerc´ ıcios resolvidos √ 5 a) Calcule log 1 27. 9 √ x √ Solu¸˜o: ca 5 1 5 log 1 27 = x ⇒ = 27 9 9 1 x √ x 3−2 = 34/5 5 = 34 ⇒ 32 4 2 3−2x = 34/5 ⇒ −2x = ⇒ x=− 5 5 ınio da fun¸˜o f (x) = logx (x2 − 4). b) Determine o dom´ ca As condi¸˜es sobre y = logb x s˜o b > 0, b = 1 e x > 0. co a ınio da fun¸˜o acima ser´ x > 0, x = 1 e x2 − 4 > 0. Portanto, o dom´ ca a A equa¸˜o x2 −4 = 0 tem solu¸˜o x = ±2. Logo x2 −4 > 0 ⇒ x < −2 ca ca ou x > 2 CEDERJ 218
- 221. Fun¸˜o logaritmo ca ´ MODULO 1 - AULA 19 Portanto, Dom(f ) = (2, ∞). -2 2 Propriedades do logaritmo Na Se¸˜o 3 vimos propriedades que decorrem diretamente da defini¸˜o. ca ca Veremos agora outras propriedades. a) Logaritmo do produto. logb (x · y) = logb x + logb y b) Logaritmo da potˆncia. e logb aw = w · logb a c) Logaritmo do quociente. x logb = logb x − logb y y 1 d) logbz a = · logb a z w w e) logbz a = · logb a z Vamos mostrar por que valem as propriedades enunciadas. Precisamos apenas trabalhar cuidadosamente com a defini¸˜o de logaritmo. ca Prova da propriedade a). Seja logb (x · y) = z, logb x = z1 e logb y = z2 . Queremos provar que z = z1 + z2 . Podemos escrever, bx = x · y, bz1 = x e bz2 = y . Logo, bz1 · bz2 = xy ⇒ bz1 +z2 = xy . Ent˜o, a bz = bz1 +z2 ⇒ z = z1 + z2 . Esta ultima igualdade era o que precis´vamos provar. ´ a Prova da propriedade b). Seja logb aw = x e w logb a = y. Precisamos provar que x = y. Temos, y bx = aw e logb a = . w 219 CEDERJ
- 222. Fun¸˜o logaritmo ca Logo, y bx = aw e b w = a . Elevando ` potˆncia w a ultima igualdade vem que a e ´ bx = aw e by = aw ⇒ x = y . Esta ultima igualdade era o que precis´vamos provar. ´ a Prova da propriedade c). Usando as propriedades a) e b) anteriores escrevemos x 1 1 logb = logb x · = logb x + logb . y y y Mas, 1 logb = logb y −1 = −1 · logb y . y Juntando os dois resultados est´ completa a prova da propriedade c). a Prova da propriedade d). 1 Seja logbz a = x e logb a = y. Precisamos provar que x = y. Temos z 1 bzx = a e logb a z = y . Ou seja 1 1 bx = a z e by = a z ⇒ x = y . Esta ultima igualdade prova a propriedade d). ´ Prova da propriedade e). Usando a propriedade b) e em seguida a propriedade d), escrevemos w logbz aw = w logbz a = logb a . z Mudan¸a de base c Todos as propriedades que vimos at´ agora envolvem logaritmos de e mesma base. Em algumas aplica¸˜es ´ interessante transformar um logaritmo co e de uma base para outra. Conseguimos isto com a propriedade: logc a logb a = , logc b onde a, b, c > 0, b = 1 e c = 1. Vamos provar este resultado. y Se logb a = x, logc a = y e logc b = z, precisamos provar que x = . z CEDERJ 220
- 223. Fun¸˜o logaritmo ca ´ MODULO 1 - AULA 19 De fato, bx = a, cy = a e cz = b ⇒ bx = cy e cz = b . Logo, bx = cy e czx = bx ⇒ zx = y . Esta ultima igualdade prova o que quer´ ´ ıamos. log2 x 3 Exemplo: Se log2 x = 3 e log2 y = 5, logy x = = · log2 y 5 Observa¸˜es: co • Os logaritmos de base 10 s˜o chamados decimais. O logaritmo decimal a de um n´ mero x (com x > 0) ´ indicado por log x (pode-se omitir o 10 na u e base). • Os logaritmos de base e, s˜o chamados logaritimos naturais ou nepe- a rianos. O logaritmo neperiano de x ´ indicado por ℓn x ou lg x. e Observa¸˜o: ca O n´ mero e ´ junto com o n´ mero π os dois mais importantes n´ meros u e u u da Matem´tica. O n´ mero e, como o n´ mero π, ´ um n´ mero irracional. a u u e u 2,71 ´ o valor que aproxima e com trˆs casas decimais exatas. e e Equa¸˜es logar´ co ıtmicas S˜o equa¸˜es envolvendo logaritmos. A maioria das equa¸˜es logar´ a co co ıtmicas, em nosso n´ de estudo, s˜o de trˆs tipos b´sicos, ou podem ser reduzidas a ıvel a e a estes tipos, fazendo algumas manipula¸˜es alg´bricas. Vamos aos trˆs tipos co e e b´sicos. a 1o tipo ¯ Logaritmos de mesma base loga f (x) = loga g(x) ⇒ f (x) = g(x). Devemos sempre observar as restri¸˜es co na base: a > 0 e a = 1. nos logaritmandos: f (x) > 0 e g(x) > 0 Exemplo: log2 (3x − 4) = log2 (x + 4). Solu¸˜o: 3x − 4 = x + 4 ⇒ x = 4. ca 4 Restri¸˜es: 3x − 4 > 0 ⇒ x > co e x + 4 > 0 ⇒ x > −4 3 Como x = 4 atende `s restri¸˜es, ent˜o o conjunto solu¸˜o S = {4}. a co a ca 221 CEDERJ
- 224. Fun¸˜o logaritmo ca 2o tipo Aplica¸˜o da defini¸˜o de logaritmo. ¯ ca ca logb (f (x) = a ⇒ f (x) = ba , Observando sempre as restri¸˜es: co na base: b>0eb=1 no logaritmando: f (x) > 0 Nestas equa¸˜es, podemos ter vari´veis no logaritmando e na base ao mesmo co a tempo. Exemplo: logx (x2 − 3x + 2) = 2 2 Solu¸˜o: Temos que x2 − 3x + 2 = x2 ⇒ −3x + 2 = 0 ⇒ x = ca 3 Restri¸˜es: co • x>0ex=1 (base) • x2 − 3x + 2 > 0 A equa¸˜o x2 − 3x + 2 = 0 tem ra´ x = 2 e x = 1, logo ca ızes x2 − 3x + 2 > 0 ⇒ x < 1 ou x > 2 y 1 2 x 2 2 O valor x = atende a estas condi¸˜es, logo o conjunto solu¸˜o ´ S = { } co ca e 3 3 3o tipo Substitui¸˜o de vari´vel. ¯ ca a Acontece quando uma substitui¸˜o do tipo y = logb x reduz o problema ca a uma equa¸˜o que sabemos resolver, como uma equa¸˜o do 2o grau. ca ca ¯ Exemplo: (log2 x)2 − 2 log2 x − 8 = 0 Solu¸˜o: Substituindo y = log2 x, temos y 2 −2y −8 = 0 ⇒ y = 4 ou y = −2. ca log2 x = x ⇒ x = 24 = 16 1 log2 x = −2 ⇒ x = 2−2 = 4 Portanto, o conjunto solu¸˜o ´ S = {1/4, 16}. ca e Inequa¸˜es logar´ co ıtmicas S˜o inequa¸˜es onde aparecem a fun¸˜o logar´ a co ca ıtmica envolvendo a vari´vel. a Vamos examinar algumas t´cnicas para resolver estas inequa¸˜es. e co CEDERJ 222
- 225. Fun¸˜o logaritmo ca ´ MODULO 1 - AULA 19 Em primeiro lugar, a fun¸˜o y = logb x, sendo inversa da exponencial, ca ´ crescente b > 1 e decrescente quando 0 < b < 1. Assim, e • se b > 1, logb f (x) > logb g(x) ⇒ f (x) > g(x) • se 0 < b < 1 logb f (x) > logb g(x) ⇒ f (x) < g(x) Isto respeitadas as restri¸˜es para existˆncia dos logaritmos. Quais sejam, co e • b > 0 e b = 1 (base) • f (x) > 0 e g(x) > 0 (logaritmando) Observa¸˜o: ca • Para reduzir uma inequa¸˜o ` forma logb f (x) > logb g(x), temos que ca a usar propriedades do produto ou do quociente (para reunir dois logaritmos), ou fazer substitui¸˜o de vari´veis y = logb x. ca a • Note que logb f (x) > a ⇒ logb f (x) > logb ba pois a = logb ba . Exerc´ ıcios resolvidos 1. Resolva a inequa¸˜o ca log3 (2x − 1) < log3 5. Solu¸˜o: log3 (2x − 1) < log3 5 ⇒ 2x − 1 < 5 ⇒ 2x < b ⇒ x < 3 ca 1 Restri¸˜o: 2x − 1 > 0 ⇒ x > ca . Portanto, o conjunto solu¸˜o S ´ ca e 2 1 S= ,3 2 2. Resolva a inequa¸˜o ca (log2 x)2 = 3 log2 x + 2 < 0. Solu¸˜o: Fazemos a substitui¸˜o y = log2 x, encontramos ca ca 2 y − 3y + 2 < 0 ⇒ 1 < y < 2 1 2 (pois y = 1 e y = 2 s˜o as ra´ de y 2 − 3y + 2 = 0). a ızes Portanto, 1 < log2 x < 2. log2 x > 1 ⇒ log2 x > log2 2 ⇒ x > 2 log2 x < 2 ⇒ log2 x < log2 4 ⇒ x < 4 A restri¸˜o no logaritmando ´ x > 0, logo o conjunto solu¸˜o ´ ca e ca e S = (2, 4). 223 CEDERJ
- 226. Fun¸˜o logaritmo ca 3. Resolva a inequa¸˜o ca log2 (x − 1) + log2 (x + 1) < 3. Solu¸˜o: Usamos a propriedade do produto para juntar os dois logarit- ca mos log2 (x − 1) + log2 (x + 1) < 3 log2 (x − 1)(x + 1) < log2 23 = log2 8 (x − 1)(x + 1) < 8 x2 − 1 < 8 x2 − 9 < 0 As solu¸˜es de x2 − 9 = 0 s˜o x = ±3 logo x2 − 9 < 0 ⇒ −3 < x < 3. co a -3 3 As restri¸˜es s˜o x − 1 > 0 ⇒ x > 1 e x + 1 > 0 ⇒ x > −1 co a O conjunto solu¸˜o ´ ca e S = (−3, 3) ∩ (1, ∞) ∩ (−1, ∞) = (1, 3). Cararcter´ ıstica e mantissa Usando uma calculadora, vemos que log 6 ≈ 0, 77815 (lembre que log 6 = log10 6). Sabendo disso, podemos calcular facilmente log 60, log 600 etc. log 60 = log 6 · 10 = log 6 + log 10 = 1 + 0, 77815 = 1, 77815 log 600 = log 6 · 100 = log 6 + log 102 = 2, 77815 Os n´ meros log 6, log 60, log 600 etc, tˆm a mesma parte decimal, que u e chamamos mantissa e diferem na parte inteira, que chamamos caracter´ıstica. Assim, caracter´ ıstica: 2 log 600 tem mantissa: 0, 77815 Nota: Observe que, se x tem 3 d´ ıgitos, ent˜o a 100 ≤ x < 1000 ⇒ 2 3 2 3 10 ≤ x < 10 ⇒ log 10 ≤ log x < log 10 ⇒ 2 ≤ log x < 3. Portanto, se x tem 3 d´ ıgitos, ent˜o 2 ≤ log x < 3. Em geral, se x ´ um a e ıgitos, ent˜o n − 1 ≤ log x < n inteiro positivo de n d´ a CEDERJ 224
- 227. Fun¸˜o logaritmo ca ´ MODULO 1 - AULA 19 Exerc´ ıcios resolvidos 1. Usando log a = 0, 3010 calcule a) log 200 b) log 0, 0128 Solu¸˜o: ca a) log 200 = log 2 · 102 = log 2 + 2 = 2, 3010 b) log 0, 0128 = log 128 × 10−4 = log 128 + log 10−4 = log 27 − 4 = −4 + 7 · log 2 = −4 + 7 × (0, 3010) = −1, 893 ıgitos do inteiro 250 . 2. Determine o n´ mero de d´ u Solu¸˜o: Calculamos seu logaritmo decimal, ca log 250 = 50 × log 2 = 50 × 0, 3010 = 15, 05 Como 15 ≤ log250 < 16, ent˜o 250 ´ um inteiro de 16 d´ a e ıgitos. Exerc´ ıcios - S´rie A e 1. Calcule: 1 √ 3 a) log3 b) log25 125 c) log 1 64 27 4 d) log13 13 · log15 1 e) log0,01 10 2. Sendo f (x) = 32x e g(x) = log4 x, calcule f (g(2)). 3. (UERJ-92) O valor de 4log2 9 ´: e a) 81 b) 64 c) 48 d) 36 e) 9 ınio da fun¸˜o f (x) = logx x2 − 3x + 2. 4. Determine o dom´ ca a3 5. Sendo logx a = 4, logx b = 2 e logx c = 1, calcule logx . b2 c2 6. Resolva a equa¸˜o log3 (2x − 1) − log3 (5x + 3) = −1 ca 7. (UNI-RIO 92) Se N(t) = N0 ekt , t ≥ 0 e N(2) = 3N0 , ent˜o o valor a de k ´: e 3 1 1 1 a) loge b) loge 3 c) loge 3 d) loge 4 e) log2 e 2 2 3 4 225 CEDERJ
- 228. Fun¸˜o logaritmo ca 8. (UFRJ-98) Sejam x e y duas quantidades. O gr´fico abaixo expressa a a varia¸˜o de log y em fun¸˜o de log x, onde log ´ o logaritmo na base ca ca e decimal. log y 6 2 2 log x Determine uma rela¸˜o entre x e y que n˜o envolva a fun¸˜o logaritmo. ca a ca 9. Usando log 3 = 0, 4771, calcule: a) log 3000 b) log 0, 003 c) log 0, 81 10. Calcule log0,04 125, usando que log 2 = 0, 3010. 11. Um n´ mero x tem logaritmo igual a 4 na base a e tem logaritmo igual u a a 8 na base · Calcule x e a. 3 x + y = 7 12. Resolva o sistema log x + log y = log 12 a a a 13. Simplifique a express˜o (logx 9) · (log81 16) · (log4 3) a 2x = 1 14. Resolva o sistema 24+y log (2x + y) = 0 a 15. (UNI-RIO 93) Se x = log3 2, ent˜o 3x + 3−x ´ igual a a e 8 5 a) b) c) 4 d) 6 e) 9 7 2 √ 16. Se log10 30 = log10 2+2 log10 3−log10 ex , a alternativa que representa o valor de x ´: e a) − loge 2 b) − loge 5 c) − loge 15 d) − loge 20 e) − loge 30 CEDERJ 226
- 229. Fun¸˜o logaritmo ca ´ MODULO 1 - AULA 19 17. (UNI-RIO 94) Um explorador descobriu, na selva amazˆnica, uma o esp´cie nova de planta e, pesquisando-a durante anos, comprovou que o e seu crescimento m´dio variava de acordo com a f´rmula A = 40 · (1, 1)t, e o onde a altura m´dia A ´ medida em cent´ e e ımetros e o tempo t em anos. Sabendo-se que log 2 = 0, 30 e log 11 = 1, 04, determine: a) a altura m´dia, em cent´ e ımetros, de uma planta dessa esp´cie aos 3 e anos de vida; b) a idade, em anos, na qual a planta tem uma altura m´dia de 1,6 m. e 18. (PUC 90) Se a = log8 225 e b = log8 15, ent˜o: a a) 2a = b b) 3a = 2b c) a = b d) 2b = a e) 3b = 2a Exerc´ ıcios - S´rie B e x+1 1. (UNI-RIO 99) Seja a fun¸˜o definida por f (x) = log2 ca · O valor 2x de x para o qual f (x) = 1 ´ tal que: e 1 1 1 1 1 a) 0 < x < b) <x< c) <x< 100 100 10 10 5 1 3 3 d) < x < e) x > 5 10 10 √ 2. (UNICAMP 93) Calcule o valor da express˜o logn (logn n n n), onde a n ´ um n´ mero inteiro, n ≥ 2. Ao fazer o c´lculo, vocˆ ver´ que esse e u a e a valor ´ um n´ mero que n˜o depende de n. e u a (a + b)2 3. (FUVEST SP) Sendo a2 + b2 = 70ab, calcule log5 , em fun¸˜o ca ab de m = log5 2 e n = log5 3. 4. (UFF 95) Sejam x, y e p n´ meros reais positivos e p = 1. Se u x+y logp (x + y) = m e logp x + logp y = n, ent˜o logp a ´ igual a: e xy m a) mn b) c) m · n d) m + n e) m − n n 5. Resolva as equa¸˜es: co a) logx (4x − 4) = 2 b) logx+2 (x2 + 4) = logx+2 (3x2 + 1) 227 CEDERJ
- 230. Fun¸˜o logaritmo ca 6. (PUC 99) Sabendo-se que log10 3 ∼ 0, 47712, podemos afirmar que o = 25 n´ mero de algarismos de 9 ´: u e a) 21 b) 22 c) 23 d) 24 e) 25 1 1 7. Se log a + log b = P , ent˜o o valor de log a + log ´: e a b 1 a) b) −P c) P d) P −1 e) P +1 P √ 8. Calcule o valor de log10 3 + log10 0, 001 − log0,1 10 10, sabendo que log 2 = 0, 3010 e log 3 = 0, 4771. 9. (CESGRANRIO 90) Sendo a e b as ra´ da equa¸˜o x2 +100x−10 = 0, ızes ca 1 1 calcule o valor de log10 + . a b 10. Sabe-se que log10 3 = 0, 477 e que log10 103 = 2, 013. O tempo no qual triplicar´ uma popula¸˜o que cresce 3% ao ano ´ de aproximadamente: a ca e a) 37 anos b) 47 anos c) 57 anos d) 67 anos e) 77 anos 11. (UNESP 92) A curva da figura representa o gr´fico da fun¸ao y = loga x a c˜ (a > 1). Dos pontos B = (2, 0) e C = (4, 0) saem perpendiculares ao eixo das abcissas, as quais interceptam a curva em D e E, respectiva- mente. Se a ´rea do trap´zio retangular BCED vale 3, provar que a a e 1 ´rea do triˆngulo ABD, onde A = (1, 0), vale · a a 2 y y = logax E D A B C x 12. (UFRN 83) Considere log 2 = 0, 3010 e log 3 = 0, 4771. Ent˜o, qual a a quantidade de algarismos do n´ mero 315 × 212 × 623 ? u 13. (PUC 93) Sabendo-se que log10 3 ∼ 0, 47712 e que N = 3100 , podemos = afirmar que o n´ mero de algarismos do inteiro N ´: u e a) 47 b) 48 c) 49 d) 50 e) 51 CEDERJ 228
- 231. Fun¸˜o logaritmo ca ´ MODULO 1 - AULA 19 14. (FUVEST 92) Seja x = 21000 . Sabendo que log10 2 ´ aproximadamente e igual a 0,30103, pode-se afirmar que o n´ mero de algarismos de x ´: u e a) 300 b) 301 c) 302 d) 1000 e) 2000 15. (PUC 93) Sabendo-se que log10 3 ∼ 0, 47712 e que N = 3100 , podemos = afirmar que o n´ mero de algarismos do inteiro N ´: u e a) 47 b) 48 c) 49 d) 50 e) 51 Gabarito S´rie A e 1) a) −3 b) 3 c) −1 d) 0 e) − 1 2 2 2) 3 3) a 4) (0, 1) ∪ (2, ∞) 2 5) 6 6) 6 7) b 8) y = 100x 9) a) 3,4771 b) −2, 5229 c) −0, 0916 4 10) b 11) a = 9, x = 9 12) x = 4 e y = 3 ou x = 3 e y = 4 13) logx 3 14) x = 5, y = −9 15) a 16) b 17) a) 53, 24 cm b) 15 anos 18) d S´rie B e 3 1) e 2) −2 3) 3m + 2n 4) e 5) a) 2, b) ± 2 6) d 2, 094 0, 349 7) = 8) −1, 9771 9) 1 10) a 11) Demonstra¸˜o ca 1, 398 0, 233 12) 29 13) b 14) c 15) b Auto-avalia¸˜o ca Antes de passar ` aula seguinte, vocˆ deve resolver todos os exerc´ a e ıcios da S´rie A. A S´rie B fica como exerc´ de aprofundamento. e e ıcio 229 CEDERJ
- 233. Trigonometria ´ MODULO 1 - AULA 20 Aula 20 – Trigonometria Introdu¸˜o ca O termo trigonometria significa, em uma tradu¸˜o literal, medidas de ca um triˆngulo. Mais especificamente, a trigonometria estuda rela¸˜es envol- a co vendo ˆngulos e raz˜es dos lados de triˆngulos semelhantes. a o a Historicamente as primeiras rela¸˜es trigonom´tricas j´ eram conheci- co e a das pelos eg´ ıpcios e babilˆnicos em 1600 A.C., aproximadamente. Na antigui- o dade, muitos avan¸os na trigonometria se devem principalmente as aplica¸˜es c co em astronomia (ver [1], [2], [3] e [4]): • Aristarco (310-230 A.C.), desenvolveu um consistente m´todo para es- e timar o raio da lua e do sol bem como de suas distˆncias relativas a a terra. • Erat´stenes (276-194 A.C.), por sua vez, calculou uma das mais famosas o estimativas para o per´ ımetro da circunferˆncia da terra e seu raio. Para e isso, comparou posi¸˜es relativas de sombras exatamente ao meio dia do co solst´ de ver˜o em duas cidades: Siene e Alexandria. Assim, obteve ıcio a que o ˆngulo α da figura abaixo era cerca de 1/50 do circulo. a a dri an ex Al α R α Siene O Sabendo que a distˆncia entre as duas cidades era cerca de 925 Km, a estimou que o per´ ımetro da terra seria de cerca de 925 x 50 = 46.250 km, sendo que o valor correto ´ de 40.075 km. e • O astrˆnomo grego Hiparco (180-125 A.C.) ´ considerado o pai da tri- o e gonometria devido as suas importantes contribui¸˜es. A ele ´ atribu´ co e ıdo a constru¸˜o da primeira tabela trigonom´trica e tamb´m uma das pri- ca e e meiras referˆncias a utilizar a medida do ˆngulo em graus (sistema e a sexagesimal). 231 CEDERJ
- 234. Trigonometria • Cl´udio Ptolomeu foi o autor do mais celebre tratado de astronomia a (e trigonometria) da antiguidade: O almagesto. N˜o h´ registros pre- a a cisos da ´poca em que viveu Ptolomeu, mas seus trabalhos provavel- e mente foram realizados no s´culo II. O almagesto apresenta o sistema e geocˆntrico, ou seja terra como centro do universo. Essa teoria per- e sistiu at´ a idade m´dia, sendo posteriormente substitu´ pela teoria e e ıda heliocˆntrica de Nicolau Cop´rnico (1473-1543). e e Agora que j´ discutimos um pouco da hist´ria da trigonometria, va- a o mos apresentar os primeiros conceitos trigonom´tricos. Para isso iniciaremos e discutindo o conceito b´sico de ˆngulo e o sistema sexagesimal (unidade de a a grau). Em seguida, apresentaremos as principais rela¸˜es trigonom´tricas em co e um triˆngulo retˆngulo: seno, cosseno, tangente, etc, bem como as principais a a rela¸˜es fundamentais entre esses elementos. co ˆ Angulos - Medidas ˆ Angulo Vamos considerar um ˆngulo AOP como origin´rio da rota¸˜o da semi- a a ca −→ − → reta OA da posi¸˜o inicial (P.I.) ` posi¸˜o terminal OP (P.T.) ca a ca P P.T. O A P.I. P P.T. O A P.I. O ˆngulo AOP ´ positivo se o sentido da rota¸˜o indicado ´ anti-hor´rio a e ca e a e negativo se o sentido da rota¸˜o ´ hor´rio. ca e a CEDERJ 232
- 235. Trigonometria ´ MODULO 1 - AULA 20 Medida de ˆngulo e arcos a Sistema sexagesimal (unidade graus) 1 ca ˆ Defini¸˜o: Angulo de 1 grau denotado por 1◦ ´ o ˆngulo e a do ˆngulo reto. a 90 O grau admite dois subm´ ltiplos: u 1 minuto denotado por ′ e definido por 1′ = do grau; 60 1 1 segundo denotado por ′′ e definido por 1′′ = do minuto = do segundo. 60 3600 Sistema circular (unidade radiano) Defini¸˜o: Um radiano ´ o ˆngulo central que subtende na circunferˆncia um ca e a e arco cujo comprimento ´ igual ao raio. Nota¸˜o: 1 rd e ca B ⌢ AB→ arco AB 1 rd O A ⌢ AB → comprimento do arco AB ⌢ AOB = 1 rd se AB = R Se α ´ um ˆngulo em radianos que intercepta na circunferˆncia um arco e a e de comprimento l, temos: B R α ⌢ O A AB= l ˆ Angulo central Comprimento do arco 1 rd – R α rd – l Logo, l = αR . Convers˜o a O ˆngulo de uma volta em torno de uma circunferˆncia em graus ´ a e e ◦ 360 . Vamos encontrar este ˆngulo em radianos. a 233 CEDERJ
- 236. Trigonometria Sabemos que o comprimento de uma circunferˆncia ´ 2πR. e e 2πR Da´ α = ı, ⇒ α = 2π. R Portanto a rela¸˜o entre os sistemas ´: ca e 360◦ ↔ 2π. Exerc´ ıcios resolvidos 1. Exprimir 120◦ em radianos. 360◦ – 2π 120◦ · 2π 2π ⇒ x= ◦ = 120◦ – x 360 3 2π Resposta: rd. 3 2. Exprimir 60◦ 15′ em radianos. (Considere π = 3, 14) ◦ 15 60◦ 15′ = 60◦ + = 60, 25◦ 60 360◦ – 2π 60, 25◦ · 2π ⇒ x= = 1, 05 60, 25◦ – x 360◦ Resposta: 1, 05rd. 3. Exprimir 1 rd em graus. (Considere π = 3, 14) Solu¸˜o ca 360◦ – 2π 360◦ 180 ⇒ x= = x – 1 2π 3, 14 1800’0 | 3 14 2300 57◦ 19′ 29′′ 102◦ 60 6120′ 2980′ Temos que 1 rd ´, aproximadamente, 57◦ 19′ 29′′ . e 154′ 60 9240′′ 2960 134′′ CEDERJ 234
- 237. Trigonometria ´ MODULO 1 - AULA 20 4. Calcular, em graus, o ˆngulo convexo formado pelos ponteiros de um a rel´gio que marca 3h 42min. o Solu¸˜o: Note que em 1h (60′) o ponteiro pequeno percorre um ˆngulo ca a 360◦ de: 12 = 30◦ . Ponteiro pequeno tempo 30 · 42 30◦ 60′ ⇒ a= = 21◦ 60 a 42′ Este ˆngulo ´ o que determina o ponteiro das horas. a e 9 a 3 b 4 8 7 5 6 b = 30 · 5 + 6 · 2 = 150 + 12 = 162◦ Da´ o ˆngulo convexo pedido ´: ı a e x = b − a = 162◦ − 21◦ = 141◦ 5. Calcular o menor ˆngulo entre os ponteiros de um rel´gio que marca a o 12h e 20min. Solu¸˜o: ca Ponteiro pequeno tempo 20 · 30 30◦ 60′ ⇒ a= = 10◦ 60 a 20′ 12 1 a 2 b 3 4 5 6 Temos que a + b = 4 · 30 = 120 ⇒ b = 120 − 10 = 110◦ . Resposta: 110◦ . 235 CEDERJ
- 238. Trigonometria Exerc´ ıcios propostos 1. Exprimir 30◦ 15′ para radianos. (Considere π = 3, 14) 2. Transformar 12◦ em radianos. 3. Achar trˆs ˆngulos, em graus, sabendo que a soma do primeiro com o e a segundo ´ 12◦ , a do segundo com o terceiro ´ 9◦ e a soma do primeiro e e π com o terceiro ´e rd. 36 4. Quantos graus mede, aproximadamente, um arco de 0, 105 rd? 2 5. Converter em graus. (Considere π = 3, 14) π 6. Mostre que o ˆngulo que o ponteiro das horas descreve, em graus, ´ a a e metade do n´ mero que marca os minutos. u 7. Encontre o menor ˆngulo formado pelos ponteiros de um rel´gio `s 2h a o a 15min. 8. Encontre o menor ˆngulo formado pelos ponteiros de um rel´gio `s 9h a o a 10min. 9. O ponteiro dos minutos mede 10 cm. Determine o comprimento do arco. Determine o comprimento do arco quando a sua extremidade descreve 12 minutos. 10. A que horas, da noite, os ponteiros de um rel´gio coincidem entre os o n´ meros 8 e 9 do mostrador? u Gabarito 1. 0, 53 rd 2. 0, 209 rd 3. 4◦ ; 8◦ ; 1◦ . 4. 6◦ 5. 36◦ 31′ 7. 22◦ 30′ 8. 145◦ 9. 12,56 cm 10. 20h 43min 37,2 segundos. CEDERJ 236
- 239. Trigonometria ´ MODULO 1 - AULA 20 Fun¸˜es trigonom´tricas de um ˆngulo agudo co e a Seja um triˆngulo retˆngulo ABC de lados a, b e c a a Considere as seguintes nota¸˜es: co C seno → sen cosseno → cos a b tangente → tg secante → sec A c B cossecante → csc cotangente → cotg b cateto oposto c cateto adjacente sen B = = cotg B = = a hipotenusa b cateto oposto c cateto adjacente a hipotenusa cos B = = sec B = = a hipotenusa c cateto adjacente b cateto oposto a hipotenusa tg B = = csc B = = c cateto adjacente b cateto oposto A partir das defini¸˜es anteriores, ´ imediato que: co e c b sen C = = cos B cotg C = = tg B a c b a cos C = = sen B sec C = = csc B a b c a tg C = = cotg B csc C = = sec B b c Sendo B + C = 90◦ (ˆngulos complementares) e as fun¸˜es associa- a co das em cada rela¸˜o chamadas de co-fun¸˜es. Ent˜o co-fun¸˜es de ˆngulos ca co a co a complementares s˜o iguais a Rela¸˜es fundamentais co Seja x um ˆngulo agudo. De acordo com as defini¸˜es das fun¸˜es, a co co podemos verificar que: I) sen2 x + cos2 x = 1 sen x II) tg x = cos x 1 cos x III) cotg x = = Auxiliares: tg x sen x 1 sec2 x = 1 + tg2 x IV) sec x = cos x csc2 x = 1 + cotg2 x 1 V) csc x = sen x 237 CEDERJ
- 240. Trigonometria Valores not´veis a sen 45◦ , cos 45◦ , tg 45◦ Considere um triˆngulo retˆngulo is´sceles de catetos l a a o C 45◦ √ l 2 l 45◦ A l B √ 2 √ ent˜o l 2 ser´ a medida da hipotenusa pois BC a a = l2 + l2 ⇒ BC = l 2. Assim, √ AC l 1 ◦ 2 a) sen B = = √ = √ ⇒ sen 45 = . BC l 2 2 2 √ AB l 1 ◦ 2 b) cos B = = √ = √ ⇒ cos 45 = . BC l 2 2 2 AC l c) tg B = = = 1 ⇒ tg 45◦ = 1. AB l sen 60◦ , cos 60◦ , tg 60◦ √ l 3 Considere um triˆngulo equil´tero de lado l, ent˜o a a a ser´ a medida a 2 da altura pois C (AC)2 = (AM)2 + (MC)2 30◦ 2 2 l 3l l l ⇒ (MC)2 = l2 − = 4 4 √ l 3 60◦ ⇒ MC = 60◦ 2 A M l B l 2 Assim: √ l 3 √ MC 3 a) sen A = = 2 ⇒ sen 60◦ = . BC l 2 l AM 2 1 b) cos A = = ⇒ cos 60◦ = . AC l 2 √ l 3 √ MC 2 c) tg A = = l ⇒ tg 60◦ = 3. AM 2 CEDERJ 238
- 241. Trigonometria ´ MODULO 1 - AULA 20 sen 30◦ , cos 30◦ , tg 30◦ No triˆngulo AMC do item anterior vem: a l AM 1 a) sen 30◦ = = 2 ⇒ sen 30◦ = . AC l 2 √ l 3 √ ◦ MC 2 ◦ 3 b) cos 30 = = ⇒ cos 30 = . AC l 2 l √ AM 2 1 3 c) tg 30◦ = = √ = √ ⇒ tg 30◦ = . MC l 3 3 3 2 Logo temos o seguinte quadro de valores: x sen x cos x tg x √ √ 1 3 3 30◦ 2 2 3 √ √ 2 2 45◦ 1 2 2 √ 3 1 √ 60◦ 3 2 2 Exerc´ ıcios resolvidos 1. Duas rodovias A e B encontram-se em O, formando um ˆngulo de a ◦ 30 . Na rodovia A existe um posto de gasolina que dista 5 km de O. Determine a distˆncia do posto de gasolina ` rodovia B. a a Solu¸˜o: ca rod B d ◦ 30 O posto rod A 5 d 1 sen 30◦ = ⇒ d = 5 · = 2, 5 km 5 2 Resposta: 2, 5 km 239 CEDERJ
- 242. Trigonometria 2. Nas figuras, calcular h e d. D h 30◦ 60◦ A 40 m B d C Solu¸˜o: ca h √ △BCD tg 60◦ = ⇒ h=d 3 d √ h 3 △ACD tg 30◦ = ⇒ h= (40 + d) ⇒ 40 + d 3 √ √ 3 √ d 3= (40 + d) ⇒ d = 20 m e h = 20 3 m. 3 √ Resposta: d = 20 m e h = 20 3 m 5 3. Sabendo que tg x = (x agudo), calcular sen x. 12 Solu¸˜o: ca Sabemos que 1 + tg2 x = sec2 x 25 169 13 1+ = sec2 x ⇒ sec2 x = ⇒ sec x = 144 144 12 12 ⇒ cos x = 13 2 2 Usando a F.F. sen x + cos x = 1 temos 144 25 sen2 x + = 1 ⇒ sen2 x = 169 169 5 ⇒ sen x = 13 cos3 a − sen3 a 4. Simplificar a express˜o y = a 1 + sen a cos a Solu¸˜o: ca (cos a − sen a)(cos2 a + cos a sen a + sen2 a) y= ⇒ 1 + sen a cos a (cos a − sen a)(1 + cos a sen a) y= = cos a − sen a 1 + sen a cos a y = cos a − sen a CEDERJ 240
- 243. Trigonometria ´ MODULO 1 - AULA 20 Exerc´ ıcios propostos 1. Considere o triˆngulo retˆngulo ABC com as dimens˜es a = 7, 5 m, a a o b = 4, 5 m e c = 6 m. Calcular o valor de tg x. C b a x A c B 2. Uma pessoa de 1, 70 m de altura observa o topo de uma ´rvore sob a um ˆngulo α. Conhecendo a distˆncia a do observador at´ ´rvore, a a e a determine a altura da ´rvore. a 3. Na figura, determine h, sendo dados α, β e d. h α β d 4. Sendo O o centro da circunferˆncia de raio unit´rio, determine o valor e a de x. C O A 15◦ x B a+b a−b 5. Sendo sen x = e csc x = , mostre que o triˆngulo ABC, de a c c lados a, b e c ´ retˆngulo. e a 6. Seja a fun¸˜o f , definida por ca kπ f (x) = sen x + cos x + cotg x + csc x − tg x − sec x, ∀x = , k ∈ Z. 2 π Determine o valor de f 3 7. Para que valores de m as ra´ da equa¸˜o 4x2 + (2 − 3m)x + m2 = 0 ızes ca s˜o a tangente e a cotangente de um mesmo ˆngulo. a a 241 CEDERJ
- 244. Trigonometria 8. Simplificar a express˜o a sen a − sen b cos a + cos b y= + cos a − cos b sen a + sen b 9. Duas crian¸as brincam em uma gangorra cuja t´bua tem 3 m de com- c a primento. Quando a gangorra toca o ch˜o forma com ele uma ˆngulo a a ◦ de 30 . Determine a altura que se eleva a crian¸a que est´ na outra c a extremidade. 10. Determine o valor de sen3 x sen5 x sen x + + + ... 2 4 Gabarito 1. 0, 75 2. 1, 70 + a tg α d tg α tg β 3. h = tg β − tg α 4. 0, 5 √ 3−3 6. 2 7. −2 8. 0 3 2 sen x 9. 10. 2 1 + cos2 x Referˆncias e 1. Boyer, C. B., Hist´ria da Matem´tica, 3o edi¸˜o, Editora Edgard Bl¨ cher o a ca u Ltda, 1974. 2. Lima, E.L.. Meu professor de matematica e outras hist´rias, 3a Edi¸˜o, o ca Publica¸˜o SBM, 1997. ca 3. Wikipedia, A enciclopedia livre, http://pt.wikipedia.org 4. Lobo da Costa,N. M. A Hist´ria da Trigonometria. Educa¸˜o Ma- o ca tem´tica em Revista - Revista da SBEM (Sociedade Brasileira de Educa¸˜o a ca Matem´tica) - Ano 10, S˜o Paulo, p. 60 - 69, 01 mar. 2003. a a CEDERJ 242
- 245. Fun¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 21 Aula 21 – Fun¸˜es Trigonom´tricas co e Introdu¸˜o ca Na se¸˜o anterior estudamos as rela¸˜es trigonom´tricas que envolvem ca co e os ˆngulos agudos de um triˆngulo retˆngulo. Nosso objetivo ´ estender estas a a a e rela¸˜es para definir as fun¸˜es trigonom´tricas para qualquer n´ mero real, co co e u e n˜o apenas ˆngulos de 0 a 90 graus . Para isso utilizaremos o importante a a conceito de radiano apresentado na se¸˜o anterior. ca No contexto hist´rico, as fun¸˜es trigonom´tricas como definiremos a o co e seguir surgiram como evolu¸˜o de diversos resultados. Entre eles podemos ca destacar os trabalhos de Fran¸ois Vi´te (1540-1603) e principalmente de Le- c e onhard Euler (1707-1783) em um dos seus mais importantes tratados: Intro- ductio in analysin infinitorum(1748). Para definirmos as fun¸˜es trigonom´tricas, inicialmente apresentamos co e o ciclo trigonom´trico e as determina¸˜es positivas e negativas de uma arco. e co A id´ia central ´ que as fun¸˜es trigonom´tricas ser˜o definidas a partir de e e co e a uma outra fun¸˜o que associa a cada n´ mero real um ponto sobre o ciclo ca u trigonom´trico. Feito isso, na se¸˜o seguinte, definiremos as fun¸˜es seno, e ca co co-seno, tangente, etc. Ciclo trigonom´trico - determina¸˜es e co Ciclo Trigonom´trico e Chamamos de ciclo trigonom´trico a uma circunferˆncia de raio unit´rio e e a na qual fixamos um ponto (A) como origem dos arcos e a adotamos o sentido anti-hor´rio como positivo. a + A (origem) O r=1 − Arco Trigonom´trico e ⌢ Chamamos de arco trigonom´trico AP ao conjunto dos infinitos arcos e de origem A e extremidade P . Esses arcos s˜o obtidos, partindo-se da origem a A e girando em qualquer sentido (positivo ou negativo) at´ a extremidade e P , seja na primeira passagem ou ap´s v´rias voltas completas no ciclo trigo- o a nom´trico. e 243 CEDERJ
- 246. Fun¸oes Trigonom´tricas c˜ e Analogamente, chamamos de ˆngulo trignom´trico AOP ao conjunto a e − → −→ dos infinitos ˆngulos de lado inicial OA e lado terminal OP . a P A O Conjunto das determina¸˜es de um arco co Seja P um ponto qualquer de um ciclo trigonom´trico de origem A. A e ⌢ medida do arco AP , de origem A e extremidade P ´, por conven¸˜o: e ca a) Positivo se o sentido do percursso de A para P for o anti-hor´rio. a b) Negativo se o sentido de percursso de A para P for hor´rio. a P P (60◦ ) P (−300◦) 60◦ 60◦ 60◦ A A A O ponto P ´ extremidade de infinitos arcos de origem A e a medida de e ⌢ cada um deles ´ chamada determina¸˜o. A medida α0 do arco AP , tal que e ca 0 ≤ α0 < 2π ´ chamada primeira determina¸˜o positiva do arco. e ca P (α0 ) A Primeira determina¸ao positiva c˜ Adicionando ` primeira medida o n´ mero 2π, que equivale a percorrer a u uma volta do sentido anti-hor´rio, obt´m-se o n´ mero α0 +2π que ´ a segunda a e u e ⌢ determina¸˜o positiva de AP . ca P (α0 + 2π) A 244 Segunda determina¸ao positiva c˜ CEDERJ
- 247. Fun¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 21 Adicionando ` primeira determina¸˜o o n´ mero 2·2π = 4π, que equivale a ca u a percorrer duas voltas no sentido anti-hor´rio, obt´m-se o n´ mero α0 + 4π a e u ⌢ que ´ a terceira determina¸˜o positiva do arco AP , e assim por diante. e ca P (α0 + 4π) A Terceira determina¸ao positiva c˜ Subtraindo da primeira determina¸˜o positiva o n´ mero 2π, que equi- ca u vale a percorrer uma volta no sentido hor´rio, obt´m-se α0 − 2π que ´ a a e e ⌢ primeira determina¸˜o negativa do arco AP . ca (α0 − 2π) P A Primeira determina¸ao negativa c˜ Subtraindo da primeira determina¸˜o positiva o n´ mero 2 · 2π = 4π, ca u que equivale a percorrer duas voltas no sentido hor´rio, obt´m-se α0 − 4π a e que ´ a segunda determina¸˜o negativa e assim por diante. e ca P A As infinitas determina¸˜es dos arcos de origem A e extremidade P s˜o: co a Determina¸˜es positivas co Determina¸˜es negativas co primeira α0 α0 − 1 · 2π segunda α0 + 1 · 2π α0 − 2 · 2π terceira α0 + 2 · 2π α0 − 3 · 2π quarta α0 + 3 · 2π α0 − 4 · 2π . . . . . . . . . Todas essas determina¸˜es s˜o do tipo αo +n·2π, com n ∈ Z, e portanto co a ⌢ o conjundo das determina¸˜es do arco trigonom´trico AP ´: co e e {α ∈ R | α = αo + n · 2π, n ∈ Z} 245 CEDERJ
- 248. Fun¸oes Trigonom´tricas c˜ e Observa¸˜es co a) Se a medida dos arcos for expressa em graus, devemos escrever α = αo + n · 360◦ , n ∈ Z. b) O n´ mero αo , utilizado no conjunto das determina¸˜es pode ser o valor u co co ´ de uma qualquer das determina¸˜es. E costume, por´m, escolher o e valor da 1a determina¸˜o positiva ou negativa. ca c) A cada ponto P est˜o associados infinitos n´ meros reais, mas a cada a u n´ mero real est´ associado um unico P . u a ´ Se a e b s˜o duas determina¸˜es quaisquer, do conjunto das deter- a co mina¸˜es, determinar a rela¸˜o entre a e b. co ca Solu¸˜o: ca a = α0 + n1 · 2π ⇒ a − b = 2π(n1 − n2 ), n1 ∈ Z, n2 ∈ Z b = α0 + n2 · 2π ⇒ a − b = 2πn ou a − b = 360◦ , n ∈ Z Def. Dois arcos a e b s˜o cˆngruos quando tem a mesma origem e a mesma a o extremidade, isto ´, diferem entre si por um n´ mero inteiro de voltas na e u circunferˆncia. e Se a e b s˜o cˆngruos ent˜o: a−b = 2kπ, k ∈ Z ou a−b = 360k, k ∈ Z. a o a Exerc´ ıcios resolvidos 1. Determinar o conjunto das determina¸˜es dos arcos de origem A e co extremidade B assinalados na figura. 7π 6 7π A x∈R|x= + n · 2π, n ∈ Z 6 P 2. Calcule a primeira determina¸˜o positiva (α0 ) dos seguintes arcos: ca 125π 97π a) 1620◦ b) c) −810◦ d) − 11 7 Solu¸˜o ca ◦ ◦ 125π 22π a) 1620 | 360 b) 11 11 180◦ 4 15π 5 11 15π α0 = 180◦ α0 = 11 97π 14π d) − 7 ◦ ◦ c) −810 | 360 7 −90◦ −2 − 13π −6 7 13π π α0 = 360◦ − 90◦ = 270◦ α0 = 2π − = 7 7 π α0 = 270◦ α0 = 7 CEDERJ 246
- 249. Fun¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 21 3. Calcular a 3a determina¸˜o positiva do arco 1910◦ . ca 1910◦ | 360◦ ⇒ 1a det. positiva α0 = 110◦ 110◦ 5 Como a 3a det. positiva ´ α0 + 2 · 360◦ vem 110◦ + 720◦ = 830◦ . e 4. Calcular a 4a determina¸˜o negativa do arco 810◦ . ca 810◦ | 360◦ ⇒ 1a det. positiva α0 = 90◦ 90◦ 2 A 4a det. negativa ´ α0 − 4 · 360◦ ⇒ 90◦ − 1440◦ = −1350◦ . e Exerc´ ıcios Propostos 1. Calcular a 1a determina¸˜o positiva dos arcos. ca a) 1630◦ b) −1430◦ c) 2300◦ 37π 2. Determine a 1a determina¸˜o negativa do arco ca . 3 ⌢ 3. Escrever o conjunto das determina¸˜es do arco AP . co P a) b) A=P A c) d) P A A P 4. Escrever em uma unica express˜o, o conjunto dos arcos assinalados, ´ a com extremidade P e Q, conforme o caso: a) b) P P π 30◦ A 4 A Q Q 5. Sabendo que π −x e 2x+π s˜o dois arcos cˆngruos. Determine o menor a o valor positivo de x. 247 CEDERJ
- 250. Fun¸oes Trigonom´tricas c˜ e Gabarito 1) a) 190◦ b) 10◦ c) 140◦ 5π 2) − 3 π 3) a) 2πn, n ∈ Z , n∈Z b) 2πn + 2 3π c) 2πn + π, n ∈ Z d) 2πn + , n∈Z 2 π 4) a) V = x ∈ R|x = kπ + , k ∈ Z 6 π b) V = x ∈ R|x = kπ + , k ∈ Z 4 2π 5) 3 Fun¸˜es Trigonom´tricas co e Introdu¸˜o ca Consideremos, no ciclo trigonom´trico de origem A, um sistema cartesi- e ano ortogonal XOY conforme mostra a figura (1). Os pontos A(1, 0), B(0, 1), A′ (−1, 0) e B ′ (0, −1) dividem o ciclo trigonom´trico em quatro quadrantes. e ⌢ Quando dizemos que um arco AP pertence ao 2◦ quadrante, por exemplo, queremos dizer que a extremidade P pertence ao segundo quadrante. y B A′ A x O B′ Figura 1 B B B B primeiro segundo terceiro quarto quadrante ′ quadrante quadrante quadrante A A A ′ A ′ A A A O O O O B′ B′ CEDERJ 248
- 251. Fun¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 21 Defini¸˜o da fun¸˜o seno ca ca ⌢ O seno de um arco trigonom´trico AP de extremidade P ´ a ordenada e e ⌢ do ponto P . Representa-se: sen AP = ON y N P ⌢ sen AP O A x A cada n´ mero real x corresponde um unico ponto P , extremidade do u ´ ⌢ arco AP de medida x. A cada ponto P , por sua vez, corresponde uma unica ´ ordenada chamada seno de x. A fun¸˜o de R em R que a cada n´ mero real ca u associa a ordenada do ponto P ´, por defini¸˜o, a fun¸˜o seno. e ca ca Em s´ ımbolo f : R → R tal que f (x) = sen(x) = ON N P sen x x A O M Observa¸˜o ca A defini¸˜o acima ´ coerente com aquela no triˆngulo retˆngulo. De ca e a a π fato, se 0 < x < ent˜o P ∈ I ◦ quadrante e al´m disso OP = 1 (raio) e a e 2 MP = ON. Assim no triˆngulo OMP retˆngulo em M, temos: a a cat. oposto MP MP sen x = ⇔ sen x = ⇔ sen x = ⇔ sen x = ON hipotenusa OP 1 N P x O M A 249 CEDERJ
- 252. Fun¸oes Trigonom´tricas c˜ e Varia¸˜o da fun¸˜o seno ca ca Enquanto o ponto P percorre a primeira volta, no sentido anti-hor´rio, a o n´ mero real x varia de 0 a 2π e o seno de x varia de −1 a 1. Observe, na u tabela a seguir, as v´rias situa¸˜es poss´ a co ıveis. Posi¸ao do c˜ Medida do arco Medida do ar- Seno de x Propriedade No ciclo tri- ponto P em graus co em radianos gonom´trico e P ≡A x = 0◦ x=0 sen x = 0 O=N A=P O seno ´ cres- e N P π cente no 1◦ P ∈ 1◦ Q 0◦ < x < 90◦ 0<x< 0 < sen x < 1 O A 2 quadrante P =N π P ≡B x = 90◦ x= sen x = 1 Valor m´ximo a O A 2 P N π 0 < sen x < 1 P ∈ 2◦ Q 90◦ < x < 180◦ <x<π O seno ´ de- e O A 2 crescente P = A′ x = 180◦ x=π sen x = 0 P O=N A 3π O seno ´ de- e O P ∈ 3◦ Q 180◦ < x < 270◦ π<x< −1 < sen x < 0 A 2 crescente P N 3π O A P = B′ x = 270◦ x= sen x = −1 Valor m´ ınimo 2 P =N 3π O seno ´ cres- e O P ∈ 4◦ Q 270◦ < x < 360◦ < x < 2π −1 < sen x < 0 A 2 cente N P CEDERJ 250
- 253. Fun¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 21 Gr´fico a Note que sen x = sen(x±2π), pois x e x±2π s˜o as medidas de arcos de a mesma extremidade e de acordo com a tabela do item anterior, concluimos que o gr´fico da fun¸˜o f : R → R tal que f (x) = sen x ´: a ca e 1 π π 3π 2π 4π 2 2 −1 e o conjunto imagem ´ {y ∈ R | − 1 ≤ y ≤ 1} e Note que 1 2 sen 30◦ = sen 390◦ 1 sen 30◦ = sen(30◦ + 360◦ ) = sen 390◦ = 2 Propriedades Do que foi apresentado anteriormente podemos concluir que a fun¸˜o ca seno ´: e a) positiva no 1◦ e 2◦ quadrantes; negativo no 3◦ e 4◦ quadrantes 100◦ 40◦ sen 40◦ > 0 sen 200◦ < 0 200◦ sen 100◦ > 0 sen 300◦ < 0 300◦ b) crescente nos 1◦ e 4◦ quadrantes e decrescente nos 2◦ e 3◦ quadrantes. c) ´ Impar pois sen(−x) = − sen x 60◦ −60◦ d) Peri´dica de per´ o ıodo 2π. 251 CEDERJ
- 254. Fun¸oes Trigonom´tricas c˜ e Exerc´ ıcios Propostos 1. Calcule: a) sen 0◦ b) sen 30◦ c) sen 45◦ d) sen 60◦ e) sen 90◦ f) sen 120◦ g) sen 150◦ h) sen 180◦ 2. Calcular o valor de: a) sen 420◦ b) sen 750◦ Gabarito √ √ √ 1 2 3 3 1 1. a) 0 b) c) d) e) 1 f) g) h) 0 2 2 2 2 2 √ 3 1 2. a) b) 2 2 Fun¸˜o Co-seno ca Defini¸˜o ca ⌢ O co-seno de um arco trigonom´trico AP de extremidade P , ´ a abscissa e e do ponto P . Representa-se ⌢ cos AP = OM P O A M A cada n´ mero real corresponde um unico ponto P , extremidade do u ´ ⌢ arco AP de medida x. A cada ponto P , por sua vez, corresponde uma unica ´ abscissa chamada co-seno de x. A fun¸˜o de R em R que a cada n´ mero real ca u x associa a abscissa do ponto P ´, por defini¸˜o, a fun¸˜o co-seno. e ca ca Em s´ ımbolo f : R → R tal que f (x) = cos(x) = OM P x O M A Obs. A defini¸˜o dada ´ coerente com aquela apresentada no triˆngulo ca e a π ◦ retˆngulo. De fato, se 0 < x < a ent˜o P pertence ao 1 quadrante e a 2 al´m disso OP = 1 (raio). e CEDERJ 252
- 255. Fun¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 21 Assim, no triˆngulo OMP retˆngulo em M, temos: a a cat. adjacente OM OM cos x = ⇔ cos x = ⇔ cos x = ⇔ cos x = OM hipotenusa OP 1 P x O M A Varia¸˜o da fun¸˜o co-seno ca ca Enquanto o ponto P percorre a primeira volta no sentido anti-hor´rio, a o n´ mero real x varia de 0 a 2π e o co-seno de x varia de −1 a 1. Observe, u na tabela a seguir as v´rias situa¸˜es poss´ a co ıveis. Posi¸ao do c˜ Medida do arco Medida do ar- Co-seno de x Propriedade No ciclo tri- ponto P em graus co em radianos gonom´trico e P ≡A x = 0◦ x=0 cos x = 1 Valor m´ximo a O A=P =M P O co-seno ´ e π 0 < cos x < 1 decrescente no P ∈ 1◦ Q 0◦ < x < 90◦ 0<x< O M A 2 1◦ quadrante P π P ≡B x = 90◦ x= cos x = 0 O=M A 2 P π O co-seno ´ e P ∈2 Q◦ ◦ 90 < x < 180 ◦ <x<π −1 < cos x < 0 A 2 decrescente no M O 2◦ Q P = A′ x = 180◦ x=π cos x = −1 Valor m´ ınimo M =P O A 3π O co-seno ´e P ∈ 3◦ Q 180◦ < x < 270◦ π<x< −1 < cos x < 0 M A 2 crescente no O 3◦ Q P 3π P = B′ x = 270◦ x= cos x = 0 O=M A 2 P 3π O co-seno ´e P ∈ 4◦ Q 270◦ < x < 360◦ < x < 2π 0 < cos x < 1 M A 2 crescente no O 4◦ Q P 253 CEDERJ
- 256. Fun¸oes Trigonom´tricas c˜ e Gr´fico a Note que cos x = cos(x ± 2π), pois x e x ± 2π s˜o as medidas de arcos a de mesma extremidade, e de acordo com a tabela anterior, concluimos que o gr´fico da fun¸˜o f : R → R tal que f (x) = cos(x) ´: a ca e 1 π 3π 5π 7π O 2 π 2 2π 3π 4π 2 2 −1 e o conjunto imagem ´ {y ∈ R | − 1 ≤ y ≤ 1} e Note que 120◦ 60◦ 1 cos 120◦ = cos(360◦ + 120◦ ) = cos 480◦ = − cos 60◦ = − 2 −1 2 1 2 Propriedades Do que foi apresentado, podemos concluir que a fun¸˜o co-seno ´: ca e a) Positiva no primeiro e quarto quadrantes. Negativa no segundo e ter- ceiro quadrantes. ◦ 110 50◦ cos 50◦ > 0 sen 110◦ < 0 cos 220◦ < 0 sen 310◦ > 0 220◦ 310◦ b) Crescente no terceiro e quarto quadrantes. Decrescente no primeiro e segundo quadrantes. 40◦ c) Par, pois cos(−x) = cos x O cos(−40◦ ) = cos 40◦ −40◦ d) Peri´dica de per´ o ıodo 2π CEDERJ 254
- 257. Fun¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 21 Exerc´ ıcios Propostos 1. Calcule a) cos 0◦ b) cos 30◦ c) cos 45◦ d) cos 90◦ e) cos 120◦ f) cos 150◦ g) cos 180◦ 2. Calcule o valor de: a) cos 780◦ b) cos 1200◦ Gabarito √ √ √ 3 2 1 3 1. a) 1 b) c) d) 0 e) − f) − g) −1 2 2 2 2 1 1 2. a) b) − 2 2 Fun¸˜o Tangente ca Defini¸˜o ca ⌢ Consideremos um arco AP com P = B e P = D e seja T a interse¸˜o ca da reta OP com o eixo das tangentes AT . ⌢ Por defini¸˜o tg AP = AT ca B P T C A O D A fun¸˜o tangente ´ tal que ca e π f : R − kπ + , k∈Z →R 2 y = tg x = AT Observe que o ponto P , numa volta completa no ciclo trigonom´trico, e faz o valor da tangente (AT ) tender a +∞ ( ou a −∞) quando o ponto P se aproxima de B ou D (onde a tangente n˜o existe). A cada meia volta a verificamos que todos os valores da tangente se repetem. 255 CEDERJ
- 258. Fun¸oes Trigonom´tricas c˜ e Conseq¨ˆncias ue Da defini¸˜o da fun¸˜o y = tg x decorre que: ca ca π Dom´ınio D(f ) = R − kπ + , k ∈ Z 2 Imagem Im(f ) = R Varia¸˜o da fun¸˜o tangente ca ca x = 90◦ x = 0◦ 0◦ < x < 90◦ P ≡B A≡P ≡T T A A O tg x = 0 tg x > 0 ∃ tg x 90◦ < x < 180◦ x = 180◦ 180◦ < x < 270◦ P T P A≡T A O P tg x < 0 tg x = 0 tg x > 0 270◦ < x < 360◦ x = 360◦ A≡P ≡T O A O A O P ≡A P T ∃ tg x tg x < 0 tg x = 0 Gr´fico a − 3π −π − π 2 2 π 2 π 3π 2 2π 5π 2 Propriedades O per´ ıodo da fun¸˜o tangente ´ π. ca e e ımpar tg(−x) = − tg x. A fun¸˜o y = tg x ´ ´ ca A fun¸˜o y = tg x ´ crescente no intervalo ca e π π kπ − < x < kπ + , k ∈ Z. CEDERJ 256 2 2
- 259. Fun¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 21 Sinais A tangente de um arco ´ positiva no 1◦ e 3◦ quadrantes e negativa no e ◦ ◦ 2 e 4 quadrantes. Exerc´ ıcios resolvidos 1. Completar o quadro abaixo: x tg x 0◦ 30◦ 45◦ 60◦ 90◦ 180◦ 270◦ 360◦ Solu¸˜o ca x tg x 0◦ 0 √ 3 30◦ 3 45◦ 1 √ 60◦ 3 90◦ ∃ 180◦ 0 270◦ ∃ 360◦ 0 √ 2. Determinar o conjunto verdade da equa¸˜o tg x = ca 3, no intervalo 0◦ ≤ x ≤ 360◦ Solu¸˜o: ca √ ◦ 3 60 240◦ √ tg x = 3 ⇒ x = 60◦ ou x = 240◦, 0◦ ≤ x ≤ 360◦ V = {60◦, 240◦ } 257 CEDERJ
- 260. Fun¸oes Trigonom´tricas c˜ e 3 3π 3. Se tg x = eπ<x< , determine o valor de cos x − sen x. 4 2 Solu¸˜o ca Seja o triˆngulo retˆngulo temos: a a 5 3 x 4 3 3 4 tg x = , sen x = e cos x = 4 5 5 3π 3 3 4 Tomando π < x < , teremos: tg x = , sen x = − e cos x = − . 2 4 5 5 4 3 1 Portanto cos x − sen x = − − − =− . 5 5 5 Exerc´ ıcios propostos 1. Determine o conjunto verdade da equa¸˜o | tg x| − 1 = 0 no intervalo ca 0 ≤ x ≤ 2π. 2. Determine o conjunto verdade da equa¸˜o sen x+cos x = 0, no intervalo ca [4, 3π]. π 3. Se 0 < α < e sen α = a. Determine tg(π − α). 2 4. Na esta¸˜o de trabalho de pintura de pe¸as de uma f´brica, a press˜o ca c a a em um tambor de ar comprimido varia com o tempo conforme a ex- π press˜o P (t) = 50 + 50 sen t − a , t > 0. Determine o instante t que 2 corresponde ao valor m´ ınimo da press˜o. a Gabarito π 3π 5π 7π 1. V = , , , 4 4 4 4 7π 11π 2. V = , 4 4 −a 3. √ 1 − a2 4. 2π CEDERJ 258
- 261. Fun¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 21 Fun¸˜es co-tangente, secante e co-secante co O estudo das fun¸˜es co-tangente, secante e co-secante pode ser feito a co partir das trˆs fun¸˜es j´ estudadas (seno, co-seno e tangente). e co a Fun¸˜o co-tangente ca 1 Sabemos que cotg x = . tg x Podemos concluir que a fun¸˜o y = cotg x = f (x), tem ca • D(f ) = R − {kπ, k ∈ Z} pois a fun¸˜o co-tangente n˜o existe quando ca a a fun¸˜o tangente ´ zero ca e (tg x = 0 ⇔ x = kπ, k ∈ Z) • Im(f ) = R, pois a fun¸˜o tangente tem imagem igual a R. ca • O per´ ıodo da fun¸˜o co-tangente ´ π. ca e • A fun¸˜o y = cotg x ´ ´ ca e ımpar, cotg(−x) = − cotg x. • Sinais A co-tangente de um arco ´ positiva no 1◦ e 3◦ quadrantes e negativa e ◦ ◦ no 2 e 4 quadrantes. Fun¸˜o secante ca 1 Sabemos que sec x = . cos x Podemos concluir que a fun¸˜o f (x) = y = sec x, tem ca π • D(f ) = R − kπ + , k ∈ Z pois a fun¸˜o secante n˜o existe quando ca a 2 a fun¸˜o co-seno ´ zero ca e π (cos x = 0 ⇔ x = + kπ, k ∈ Z) 2 • Im(f ) = {y ∈ R | y ≤ −1 ou y ≥ 1}, pois a fun¸˜o co-seno tem ca imagem com valores −1 ≤ y ≤ 1. • O per´ ıodo da fun¸˜o secante ´ 2π. ca e • A fun¸˜o y = sec x ´ par, sec(−x) = sec x. ca e • Sinais A secante de um arco ´ positiva no 1◦ e 4◦ quadrantes e negativa no 2◦ e ◦ e 3 quadrantes. 259 CEDERJ
- 262. Fun¸oes Trigonom´tricas c˜ e Fun¸˜o co-secante ca 1 Sabemos que csc x = . sen x Podemos concluir que a fun¸˜o f (x) = y = csc x, tem: ca • D(f ) = R − {kπ, k ∈ Z} pois a fun¸˜o co-secante n˜o existe quando a ca a fun¸˜o seno ´ zero ca e (sen x = 0 ⇔ x = kπ, k ∈ Z) • Im(f ) = {y ∈ R | y ≤ −1 ou y ≥ 1}, pois a fun¸˜o seno tem imagem ca com valores −1 ≤ y ≤ 1. • O per´ ıodo da fun¸˜o co-secante ´ 2π. ca e • A fun¸˜o y = csc x ´ ´ ca e ımpar, csc(−x) = − csc x. • Sinais A co-tangente de um arco ´ positiva no 1◦ e 2◦ quadrantes e negativa e ◦ ◦ no 3 e 4 quadrantes. Exerc´ ıcios resolvidos 1. Resolver a equa¸˜o sec x = 2, x ∈ [0, 2π]. ca Solu¸˜o ca sec x = 2 1 1 1 ⇒ = 2 ⇒ cos x = sec x = cos x 2 cos x π 3 5π 3 π 5π Para 0 ≤ x ≤ 2π, temos V = , . 3 3 π 2. Se x = , calcular o valor da express˜o a 6 E = sec x + cotg x + csc(3x) Solu¸˜o ca π 2π π π π π E = sec + cotg + csc 3 · = sec + cotg + csc 6 6 6 6 3 2 1 1 1 √ = + π + = 3+1 cos π 6 tg 3 sen π 2 CEDERJ 260
- 263. Fun¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 21 √ 7 3π 3. Se cos x = e < x < 2π. Determine o valor de cotg x. 3 2 Solu¸˜o ca √ 2 √ 2 2 7 7 2 2 sen x = 1 − cos x = 1 − = 1− = ⇒ sen x = ± , 3 9 9 3 √ 3π 2 cos x como < x < 2π ent˜o sen x = − a e, da´ cotg x = ı, = √ 2 3 sen x 7 3 7 √ = − . − 2 2 3 √ 4. Resolver a inequa¸˜o 2 sen x − 3 ≥ 0 para 0 ≤ x ≤ 2π. ca √ √ 3 Solu¸˜o 2 sen x − 3 ≥ 0 ⇒ sen x ≥ ca . 2 2π π 3 √ 3 3 2 π 2π Para 0 ≤ x ≤ 2π, temos: V = x∈R| ≤x≤ . 3 3 Exerc´ ıcios propostos √ π 2 6 1. Se < x < π e sen x = , determine o valor de sec x. 2 5 2. Resolver a inequa¸˜o 2 cos x + 1 < 0, para 0 ≤ x ≤ 2π. ca 1 3. Para que valores de x, 0 ≤ x ≤ 2π, a fun¸˜o f (x) = √ ca existe no sen x campo dos n´ meros reais? u 4. Resolver a inequa¸˜o tg x ≥ 1, para 0 ≤ x ≤ 2π. ca Gabarito 1. −5 2π 4π 2. V = x∈R <x< 3 3 3. 0 < x < π π π 5π 3π 4. ≤ x < ou ≤x< . 4 2 4 2 261 CEDERJ
- 265. Rela¸oes Fundamentais e Redu¸˜o ao 1◦ quadrante c˜ ca ´ MODULO 1 - AULA 22 Aula 22 – Rela¸˜es Fundamentais e Redu¸˜o co ca ao 1◦ quadrante Rela¸˜es Fundamentais co Introdu¸˜o ca As identidades trigonom´tricas estabelecem rela¸˜es de igualdade en- e co tre as fun¸˜es trigonom´tricas. Atrav´s destas identidades ´ poss´ co e e e ıvel, por exemplo, simplificar express˜es. J´ estudamos as rela¸oes fundamentais para o a c˜ triˆngulo retˆngulo. Vamos agora estudar as rela¸˜es fundamentais no c´ a a co ırculo trigonom´trico. e Rela¸˜es Fundamentais envolvendo seno,co-seno e tangente co Teorema 1 Para todo x ∈ R, vale a rela¸˜o ca sen2 x + cos2 x = 1 Prova y kπ a) Se x = , k ∈ Z temos o triˆngulo retˆngulo a a P 2 OP1 P , usando o teorema de Pit´goras vem: a x O P1 x 2 2 2 OP1 + P1 P = OP ⇒ cos2 x + sen2 x = 1 kπ b) Se x = , k ∈ Z, podemos verificar diretamente 2 Se x = 0 ⇒ sen2 x + cos2 x = 0 + 1 = 1 π Se x = ⇒ sen2 x + cos2 x = 1 + 0 = 1 2 Se x = π ⇒ sen2 x + cos2 x = 02 + (−1)2 = 1 3π Se x = ⇒ sen2 x + cos2 x = (−1)2 + 02 = 1 2 Logo vale a rela¸˜o sen2 x + cos2 x = 1. ca 263 CEDERJ
- 266. Rela¸oes Fundamentais e Redu¸˜o ao 1◦ quadrante c˜ ca Teorema 2 π Para todo x ∈ R, x = kπ + , k ∈ Z, vale a rela¸˜o ca 2 sen x tg x = cos x Prova a) Se x = kπ, k ∈ Z temos P T △OAT ∼ △OP1P x A O P1 AT P1 P tg x sen x sen x = ⇒ = ⇒ tg x = OA OP1 1 cos x cos x Vale a rela¸˜o em qualquer quadrante que estiver x. ca sen x b) Se x = kπ, k ∈ Z, temos tg x = 0 = cos x Rela¸˜es Fundamentais envolvendo cotangente, secante, cossecante co 1. Dado um n´ mero real x, x = kπ, k ∈ Z, seja M sua imagem no c´ u ırculo trigonom´trico. Consideremos a reta OM e seja C sua interse¸˜o com e ca o eixo d da figura. B C d M x A' A O Denominamos cotangente de x e indicamos por cotg x a medida alg´brica e do segmento BC. Denominamos cossecante de x e indicamos por csc x a medida alg´brica do segmento OC. e π 2. Dado um n´ mero real x, x = kπ + , k ∈ Z, seja M sua imagem no u 2 c´ ırculo trigonom´trico. Consideremos a reta l que passa pelos pontos e A e T da figura. T M x A O l Seja T a interse¸˜o da reta l com OM. Denominamos secante de x e ca indicamos por sec x a medida alg´brica de OT . e CEDERJ 264
- 267. Rela¸oes Fundamentais e Redu¸˜o ao 1◦ quadrante c˜ ca ´ MODULO 1 - AULA 22 Teorema 3 Para todo x ∈ R, x = kπ, k ∈ Z, vale a rela¸˜o ca y cos x B Cd cotg x = sen x M1 M x Prova O x π a) Se x = kπ + , k ∈ Z temos 2 △OBC ∼ △OM1M BC M1 M cotg x cos x ⇒ = ⇒ = OB OM1 1 sen x Vale a rela¸˜o em qualquer quadrante que estiver x. ca π cos x b) Se x = kπ + , k ∈ Z, temos cotg x = 0 = 2 sen x Teorema 4 π y Para todo x ∈ R, x = kπ + , k ∈ Z, vale a rela¸˜o ca 2 T M 1 sec x = cos x x O M1 A x Prova a) Se x = kπ, k ∈ Z temos △OM1 M ∼ △OAT OM OM1 1 cos x 1 ⇒ = ⇒ = ⇒ sec x = OT OA sec x 1 cos x Vale a rela¸˜o em qualquer quadrante que estiver x. ca b) Se x = kπ, k ∈ Z, temos que sec x = 1 = cos x (k par) ou sec x = −1 = cos x (k ´ ımpar). 1 Logo, sec x = . cos x Teorema 5 B C Para todo x ∈ R, x = kπ, k ∈ Z, vale a rela¸˜o ca M1 M x A 1 O csc x = sen x 265 CEDERJ
- 268. Rela¸oes Fundamentais e Redu¸˜o ao 1◦ quadrante c˜ ca Prova π a) Se x = kπ + , k ∈ Z temos 2 △OM1M ∼ △OBC OC OB csc x 1 1 ⇒ = ⇒ = ⇒ csc x = OM OM1 1 sen x sen x Vale a rela¸˜o em qualquer quadrante que estiver x. ca π 1 1 b) Se x = kπ+ , k ∈ Z temos csc x = = 1 (k par), csc x = = −1 2 sen x sen x (k ´ ımpar) kπ Corol´rio Para todo x ∈ R, x = a , valem as rela¸˜es: co 2 1 cotg x = tg x tg2 x + 1 = sec2 x 1 + cotg2 x = csc2 x 1 cos2 x = 1 + tg2 x tg2 x sen2 x = 1 + tg2 x Prova cos x 1 1 cotg x = = sen x = sen x cos x tg x sen2 x sen2 x + cos2 x 1 tg2 x + 1 = 2x +1= 2x = = sec2 x cos cos cos2 x cos2 x sen2 x + cos2 x 1 1 + cotg2 x = 1 + 2x = 2x = = csc2 x sen sen sen2 x 1 1 cos2 x = 2x = 2 sec tg x + 1 sen2 x 1 tg2 x sen2 x = cos2 x · = cos2 x tg2 x = · tg2 x = cos2 x 1 + tg2 x 1 + tg2 x Exerc´ ıcios resolvidos 3 π 1. Sabendo que sen x = e < x < π, calcular as demais fun¸˜es co 5 2 circulares de x. π Solu¸˜o ca < x < π ⇒ cos x < 0 2 CEDERJ 266
- 269. Rela¸oes Fundamentais e Redu¸˜o ao 1◦ quadrante c˜ ca ´ MODULO 1 - AULA 22 Temos √ 9 4 cos x = − 1 − sen2 x = − 1 − =− 25 5 3 sen x 3 tg x = = 54 = − cos x −5 4 cos x 4 cotg x = =− sen x 3 1 1 5 sec x = = 4 =− cos x −5 4 1 1 5 csc x = = 3 = sen x 5 3 3 3π 2. Sabendo que tg x = e π < x < , calcular as demais fun¸˜es co 4 2 circulares de x. 1 1 4 Solu¸˜o ca cotg x = = 3 = tg x 4 3 3π J´ que π < x < a ⇒ sec x < 0 2 9 5 sec x = − 1 + tg2 x = − 1 + =− 16 4 1 4 cos x = =− sec x 5 3 4 3 sen x = tg x · cos x = − =− 4 5 5 1 5 csc x = =− sen x 3 √ 3 2 3. Sabendo que csc x = , calcular o valor da express˜o y = sen2 x + a 2 2tg2 x 1 2 4 csc x = ⇒ sen x = √ ⇒ sen2 x = sen x 3 2 18 4 2 2 4 14 4 2 cos x = 1 − sen x = 1 − = ⇒ tg2 x = 18 14 = = 18 18 18 14 7 Ent˜o a 4 2 4 4 28 + 72 100 50 y= +2· = + = = = 18 7 18 7 126 126 53 4. Calcular m de modo que sen x = 2m + 1 e cos x = 4m + 1. Solu¸˜o ca sen2 x + cos2 x = 1 ⇒ (2m + 1)2 + (4m + 1)2 = 1 √ 2 −12 ± 144 − 80 ⇒ 20m + 12m + 1 = 0 ⇒ m = 40 1 1 ⇒ m = − ou m = − 2 10 267 CEDERJ
- 270. Rela¸oes Fundamentais e Redu¸˜o ao 1◦ quadrante c˜ ca 5. Dado que sen x · cos x = k, calcular o valor de y = sen4 x + cos4 x e z = sen6 x + cos6 x. Solu¸˜o ca Como a2 + b2 = (a + b)2 − 2ab temos: y = (sen2 x)2 + (cos2 x)2 = (sen2 x + cos2 x)2 − 2sen2 xcos2 x = 1 − 2k 2 Como a3 + b3 = (a + b)(a2 − ab + b2 ) temos z = (sen2 x)3 + (cos2 x)3 = (sen2 x + cos2 x)(sen4 x − sen2 xcos2 x + cos4 x) z = sen4 x + cos4 x − sen2 xcos2 x = y − k 2 = 1 − 2k 2 − k 2 Logo z = 1 − 3k 2 Exerc´ ıcios propostos 7 3π 1. Sabendo que sen x = − e π < x < , calcular o valor da express˜o a 25 2 tg x · cos x y= . (1 + cos x)(1 − cos x) √ 1 m+1 2. Sendo cos x = e sen x = , determinar m. m m 1 csc a − sen a 3. Sendo tg a = , calcular y = . 2 sen a − cos a 4. Se 5 sec x − 3tg2 x = 1, calcular cos x. 5. Se sen x + cos x = m e sen x · cosx = n, obter uma rela¸˜o entre m e n, ca independente de x. Gabarito 25 1. − 7 2. m = 2 ou m = −1 3. y = −4 1 4. cos x = 2 5. m2 = 1 + 2n CEDERJ 268
- 271. Rela¸oes Fundamentais e Redu¸˜o ao 1◦ quadrante c˜ ca ´ MODULO 1 - AULA 22 Identidades Defini¸˜o ca Sejam f e g duas fun¸˜es de dom´ co ınios D1 e D2 , respectivamente. Dize- mos que f ´ idˆntica a g, e indicamos f ≡ g, se e somente se f (x) = g(x), ∀x e e em que ambas as fun¸˜es est˜o definidas. co a f ≡ g ⇔ f (x) = g(x), ∀x ∈ D1 ∩ D2 . Existem basicamente trˆs processos para provar a identidade de f ≡ g. e Conforme a dificuldade da demonstra¸˜o escolhemos o m´todo mais ade- ca e quado entre os seguintes. 1◦ ) Partimos de um dos membros (geralmente o mais complicado) da iden- tidade e o transformamos no outro. 2◦ ) Transformamos o 1◦ membro (f ) e, separadamente, o 2◦ membro (g), chegando com ambos a mesma express˜o (h). a 3◦ ) Construimos a fun¸˜o h = f − g e provamos que h ≡ 0. ca Exerc´ ıcios resolvidos 1. Provar que tg x + cotg x = sec x · csc x. Solu¸˜o: ca Vamos aplicar o 1◦ m´todo. e sen x cos x sen2 x + cos2 x 1 1 tg x+cotg x = + = = · = sec x·csc x cos x sen x sen x · cos x sen x cos x ⇒ tg x + cotg x = sec x · csc x 2. Provar que (1 − cos2 x)(1 + tg2 x) = tg2 x. Solu¸˜o ca 1 (1 − cos2 x)(1 + tg2 x) = sen2 x · sec2 x = sen2 x · = tg2 x cos2 x 2 3. Provar que (sen x + cos x)2 = +1 sec x · csc x Solu¸˜o ca (sen x + cos x)2 = sen2 x + 2 sen x cos x + cos2 x = 1 + 2 sen x cos x 2 2 +1= 1 1 + 1 = 2 sen x cos x + 1 sec x csc x cos x · sen x 2 Logo, (sen x + cos x)2 = + 1. sec x csc x 269 CEDERJ
- 272. Rela¸oes Fundamentais e Redu¸˜o ao 1◦ quadrante c˜ ca Exerc´ ıcios propostos 1. Provar que a) (1 − sen2 x)(1 + cotg2 x) = cotg2 x (csc2 x − cotg2 x)(sec2 x − tg2 x) b) = tg x + cotg x cos x · sen x c) sen4 x − cos4 x = sen2 x − cos2 x Redu¸˜o ao 1◦ quadrante ca Introdu¸˜o ca Dado um ˆngulo no c´ a ırculo trigonom´trico ´ sempre poss´ fazˆ-lo cor- e e ıvel e π responder a outro no intervalo 0, . Desse modo, fun¸˜es trigonom´tricas co e 2 s˜o calculadas para qualquer valor, reduzindo o ˆngulo dado ao 1◦ quadrante. a a ˆ Angulo no 2◦ quadrante Vamos, por exemplo, calcular sen 150◦ . Inicialmente, marcamos o ˆngulo de 150◦ no c´ a ırculo trigonom´trico, e ⌢ determinando o arco AB. y B M C 150◦ α A O x Pela extremidade B do arco, tra¸amos uma paralela ao eixo x, obtendo c C. O ˆngulo α ´ o correspondente a 150◦ no 1◦ quadrante. Como o ˆngulo a e a α ´ o suplementar de 150◦ , ent˜o e a α = 180◦ − 150◦ ⇒ α = 30◦ 1 Logo, sen 30◦ = sen 150◦ = OM ⇒ = sen 150◦ . 2 Note que se o ˆngulo α ´ o correspondente ao ˆngulo no 1◦ quadrante a e a ent˜o a sen(180◦ − α) = sen α. CEDERJ 270
- 273. Rela¸oes Fundamentais e Redu¸˜o ao 1◦ quadrante c˜ ca ´ MODULO 1 - AULA 22 ˆ Angulo no 3◦ quadrante Vamos, agora, calcular cos 240◦ . Inicialmente, marcamos o ˆngulo α = 240◦ no c´ a ırculo trigonom´trico, e ⌢ determinando o arco AB. y 240◦ A O x B Prolongando o raio OB, encontramos C e determinamos o correspon- dente de 240◦ no 1◦ quadrante. y C β A x 240◦ O B Como o ˆngulo β ´ o explementar de 240◦, ent˜o β = 240◦ −180◦ = 60◦ . a e a y Considere a figura C Temos que △OMC ≡ △OM ′ B pois 240◦ 60◦ M′ OB = OC O M A x ˆngulo de 90◦ nos dois triˆngulos (caso especial) a a ′ M OB = M OC. B 1 Da´ cos 240◦ = − cos 60◦ = − . ı 2 Note que qualquer ˆngulo no 3◦ quadrante temos que a cos(180◦ + β) = − cos β onde β ´ o correspondente do ˆngulo dado no 1◦ quadrante. e a 271 CEDERJ
- 274. Rela¸oes Fundamentais e Redu¸˜o ao 1◦ quadrante c˜ ca ˆ Angulo no 4◦ quadrante Vamos calcular tg 330◦ . Inicialmente, marcamos o ˆngulo α = 330◦ no c´ a ırculo trigonom´trico, e ⌢ determinando o arco AB. y 330◦ A O x B Pela extremidade B do arco, tra¸amos uma paralela ao eixo y, obtendo c C. O ˆngulo β ´ o correspondente de 330◦ na igualdade. a e y C 330◦ β O x Como β ´ o replementar de 330◦ ent˜o β = 360◦ − 330◦ = 30◦ . e a y Considere a figura Temos que △OAT ≡ △OAT ′ pois CT 330◦ ˆngulo de 90◦ nos dois triˆngulos (ALA) 30◦ A x a a O T OA = AOT ′ BT ′ OA comum Ent˜o |AT | = |AT ′ |. a 1 Logo, tg 330◦ = − tg 30◦ = − . 2 Note que para qualquer ˆngulo no 4◦ quadrante temos que a tg α = − tg(360◦ − α), onde α ´ o correspondente do ˆngulo dado no 1◦ quadrante. e a CEDERJ 272
- 275. Rela¸oes Fundamentais e Redu¸˜o ao 1◦ quadrante c˜ ca ´ MODULO 1 - AULA 22 Resumindo: a ˆ Quadrante do ˆngulo x Angulo corresponde na 1a volta Procedimento 2◦ suplementar a x 180◦ − x 3◦ explementar a x x − 180◦ 4◦ replementar a x 360◦ − x Exerc´ ıcios resolvidos 1. Calcular a) sen 135◦ b) cos 135◦ c) tg 135◦ Solu¸˜o ca Como 135◦ ∈ 2◦ quadrante, vamos calcular o suplemento de 135◦ α = 180◦ − 135◦ = 45◦ No 2◦ quadrante o cosseno e a tangente s˜o negativos e o seno ´ positivo, a e ent˜o a √ ◦ ◦ 2 sen 135 = sen 45 = 2 √ ◦ ◦ 2 cos 135 = − cos 45 = − 2 tg 135◦ = − tg 45◦ = −1 cos 2x + tg2 4x 7π 2. Calcular o valor da express˜o y = a , sabendo que x = . 1 + sen 3x 3 7π 7 · 180◦ Solu¸˜o ca x= = = 420◦ 3 3 Como 420◦ ultrapassa a 1a volta, vamos reduz´ 420◦ − 360◦ = 60◦ . ı-lo Substituindo o ˆngulo (60◦ ) na express˜o, vem: a a cos 120◦ + tg2 240◦ y= (1) 1 + sen 180◦ Temos que cos 120◦ = − cos 60◦ , j´ que 120◦ ∈ 2◦ quadrante e o cosseno a ´ negativo. e tg 240◦ = tg(240◦ − 180◦ ) = tg 60◦ , j´ que 240◦ ∈ 3◦ quadrante e a a tangente ´ positiva. e sen 180◦ = 0 Substituindo em (1) os valores obtidos, temos 1 √ − 2 + ( 3)2 5 y= = 1+0 2 273 CEDERJ
- 276. Rela¸oes Fundamentais e Redu¸˜o ao 1◦ quadrante c˜ ca 3π 3. Mostre que sen −x = − cos x. 2 Solu¸˜o ca Considere um arco x ∈ 1◦ quadrante. y B x A x 3π A partir de x, marcamos − x. 2 y △ONB ≡ △OMC pois 3π 2 −x B x OC = OB caso especial N x O O NB = C MO = 90◦ M C x B ON = C OM 3π ent˜o sen a −x = − cos x j´ que OM = −ON. a 2 π sen 2 − x · cos(π − x) 4. Simplificar a express˜o a . tg(−x) Solu¸˜o ca Vamos simplificar cada uma das fun¸˜es trigonom´tricas da express˜o, co e a ◦ considerando x ∈ 1 quadrante. y C M π B ⌢ π sen −x AC= −x 2 x 2 O NA x Temos que △ONB ≡ △OMC. π Ent˜o ON = OM, da´ sen a ı − x = cos x. 2 cos(π − x) = − cos x, j´ que π − x ∈ 2◦ quadrante a tg(−x) = tg(360 − x) = − tg x, j´ que 360◦ − x ∈ 4◦ quadrante. ◦ a Substituindo esses valores na express˜o dada vem: a cos x · (− cos x) −cos2 x cos3 x = x = + . − tg x − sen x cos sen x CEDERJ 274
- 277. Rela¸oes Fundamentais e Redu¸˜o ao 1◦ quadrante c˜ ca ´ MODULO 1 - AULA 22 Exerc´ ıcios propostos 1. Calcule: a) cos 150◦ c) sen 240◦ b) tg 210◦ d) csc 300◦ 2. Calcule sen 1920◦ 3 π 3. Se cos x = , calcular sen +x . 5 2 4. Calcule x = cos 20◦ + cos 40◦ + cos 60◦ + . . . + cos 180◦ 5. Calcule o valor das express˜es: o sen 60◦ + tg 315◦ a) y = cotg(−45◦ ) + cos 210◦ sen 45◦ · tg 45◦ · cotg 45◦ b) y = cos 210◦ · sec 240◦ · csc 300◦ 6. Simplificar a express˜o: a sen(2π − x) · cos(π − x) a) y = tg(π − x) cotg(2π − x) 9π 15π b) sen − cos x + · sen(7π − x) 2 2 Gabarito √ √ √ √ 3 3 3 2 3 1. a) − b) c) − d) − 2 3 2 3 √ 3 2. 2 3 3. 5 4. x = −1 √ √ 2 5. a) 7 − 4 3 b) − 4 6. a) sen x · cos x b) cos2 x 275 CEDERJ
- 279. Transforma¸oes c˜ ´ MODULO 1 - AULA 23 Aula 23 – Transforma¸˜es co Fun¸˜es Trigonom´tricas de arcos: soma; diferen¸a; du- co e c plo; triplo; metade. Transforma¸˜o em produto ca F´rmula da Adi¸˜o o ca Cosseno da Soma Sejam C, D e E os pontos do ciclo associados aos n´ meros a, a + b e u −b, respectivamente. Em rela¸˜o ao eixo cartesiano XOY as coordenadas ca desses pontos s˜o: a y B a+b D C a C = (cos a, sen a) A′ A D = (cos(a + b), sen(a + b)) 0 x E = (cos b, − sen b) −b A = (1, 0) B E ′ ⌢ ⌢ Os arcos AD e EC tˆm a mesma medida, portanto, as cordas AD e e CE s˜o iguais, ent˜o: a a d2 2 2 2 AD = (xD − xA ) + (yD − yA ) = [cos(a + b) − 1] + [sen(a + b) − 0] 2 = 2 − 2 cos(a + b) dEC = (xC − xE )2 + (yC − yE )2 = [cos a − cos b]2 + [sen a + sen b]2 2 = 2 − 2 cos a · cos b + 2 · sen a · sen b Como dAD = dEC ⇒ 2 − 2 cos a cos b + 2 sen a sen b = 2 − 2 cos(a + b). Da´ cos(a + b) = cos a cos b − sen a sen b . ı Cosseno da Diferen¸a c cos(a − b) = cos(a + (−b)) = cos a · cos(−b) − sen a · sen(−b) = cos a cos b + sen a sen b ent˜o cos(a − b) = cos a cos b + sen a sen b a 277 CEDERJ
- 280. Transforma¸oes c˜ Seno da Soma π π sen(a + b) = cos − (a + b) = cos −a −b 2 2 π π = cos − a · cos b + sen − a · sen b 2 2 ent˜o sen(a + b) = sen a · cos b + sen b · cos a a Seno da Diferen¸a c sen(a − b) = sen(a + (−b)) = sen a cos(−b) + sen(−b) cos a Como cos(−b) = cos b e sen(−b) = − sen b ent˜o a sen(a − b) = sen a cos b − sen b cos a . Tangente da Soma sen(a + b) sen a cos b + sen b cos a tg(a + b) = = cos(a + b) cos a cos b − sen a sen b Dividindo o numerador e o denominador por cos a cos b = 0, vem tg a + tg b tg(a + b) = 1 − tg a tg b π Observa¸˜o: a, b e (a + b) devem ser diferentes de kπ + ca , k ∈ Z. 2 Tangente da Diferen¸a c tg a + tg(−b) tg(a − b) = tg(a + (−b)) = 1 − tg a · tg(−b) Como tg(−b) = − tg b temos tg a − tg b tg(a − b) = 1 + tg a tg b π Observa¸˜o: a, b e (a − b) devem ser diferentes de kπ + ca ,k∈Z 2 C´lculo de cotg(a + b) a cos(a + b) cos a cos b − sen a sen b cotg(a + b) = = sen(a + b) sen a cos b + sen b cos a Dividindo o numerador e o denominador por sen a sen b = 0, vem: cotg a cotg b − 1 cotg(a + b) = cotg a + cotg b Observa¸˜o: a, b e (a + b) devem ser diferentes de kπ, k ∈ Z. ca CEDERJ 278
- 281. Transforma¸oes c˜ ´ MODULO 1 - AULA 23 Cotangente da Diferen¸a c cotg a · cotg(−b) − 1 cotg(a − b) = cotg(a + (−b)) = cotg a + cotg(−b) Como cotg(−b) = − cotg b temos cotg a · cotg b + 1 cotg(a − b) = cotg b − cotg a Observa¸˜o: a, b e (a − b) devem ser diferentes de kπ, k ∈ Z. ca Exerc´ ıcios Resolvidos 1. Calcular a) cos 75◦ b) sen 15◦ Solu¸˜o ca ◦ ◦ ◦ ◦ ◦ ◦ ◦ a) cos 75 = cos(45 + 30√ = cos 45 cos 30 − sen 45 sen 30 = √ √ √ ) √ √ √ 2 3 2 1 6 2 6− 2 = · − · = − ⇒ cos 75◦ = 2 2 2 2 4 4 4 ◦ ◦ ◦ ◦ 30◦ ◦ b) sen 15 = sen(45 − 30 ) = sen 45 cos √ − sen 30 cos 45 ◦ √ √ √ √ 2 3 1 2 6− 2 = · − · = 2 2 2 2 4 3 1 2. Calcular cos(a + b), sendo dado sen a = − e cos b = − , sendo que 5 3 a ∈ 3◦ quadrante e b ∈ 3◦ quadrante. Solu¸˜o ca 1◦ ) C´lculo de cos a a √ 4 cos a = − 1 − sen2 a = − 5 2◦ ) C´lculo de sen b a √ √ 2 2 sen b = − 1 − cos2b = − 3 3◦ ) C´lculo de cos(a + b) a √ 4 1 3 2 2 cos(a + b) = cos a cos b − sen a sen b = − · − − − − 5 3 5 3 √ √ 4 6 2 4−6 2 =+ − = 15 15 15 279 CEDERJ
- 282. Transforma¸oes c˜ 2 4 3. Sabendo que tg a = e sen b = − com b ∈ 4◦ quadrante. Calcular 3 5 tg(a + b). Solu¸˜o ca √ 3 1◦ ) cos b = + 1 − sen2 b = + 5 4 −5 4 2◦ ) tg b = 3 = − +5 3 2 ◦ tg a + tg b 3 −43 6 3 ) tg(a + b) = = 2 4 =− 1 − tg a tg b 1 − 3 · −3 17 Exerc´ ıcios Propostos 1. Determine o valor de: a) sen 75◦ b) cos 15◦ c) tg 15◦ 2. Calcular y = sen 105◦ − cos 75◦ π 3 3. Calcular sen x, sabendo-se que x+y = e sen y = , x ∈ 1◦ quadrante. 4 5 4. Se tg(x + y) = 33 e tg x = 3, determine tg y. 15 3 π 3π 5. Sabendo que sen x = , sen y = − , 0 < x < e π < y < . 17 5 2 2 Calcular sen(x + y), cos(x + y) e tg(x + y) 6. Se a e b s˜o ˆngulos agudos e positivos, provar que: a a sen(a + b) < sen a + sen b. Gabarito √ √ √ √ 6+ 2 6+ 2 √ 1. a) b) c) 2 − 3 4 4 √ 2 2. y = 2 √ 2 3. 10 4. 0,3 84 13 84 5. sen(x + y) = − , cos(x + y) = , tg(x + y) = − 85 85 13 6. Demonstra¸˜o ca CEDERJ 280
- 283. Transforma¸oes c˜ ´ MODULO 1 - AULA 23 Arco Duplo Trata-se de obter as express˜es das fun¸˜es trigonom´tricas dos arcos o co e ´ da forma 2a. E um caso particular das f´rmulas de adi¸˜o, ´ suficiente fazer o ca e a = b. C´lculo de cos 2a a cos 2a = cos(a + a) = cos a cos a − sen a sen b ⇒ cos 2a = cos2 a − sen2 a cos 2a = cos2 a − sen2 a C´lculo de sen 2a a sen 2a = sen(a + a) = sen a cos a + sen a cos a ⇒ sen 2a = 2 sen a cos a sen 2a = 2 sen a cos a C´lculo tg 2a a tg a + tg a 2 tg a tg 2a = tg(a + a) = = 1 − tg a · tg a 1 − tg2 a π a = kπ + , k ∈ Z 2 tg a 2 tg 2a = 2 , e 1 − tg a a = kπ + π , k ∈ Z 4 Arco Triplo Trata-se de obter as express˜es das fun¸˜es trigonom´tricas dos arcos o co e da forma 3a. C´lculo de cos 3a a Sabemos que: cos2 a − sen2 a = cos 2a ⇒ cos 2a = 2 cos2 a − 1 e sen 2a = 2 sen a cos a Logo, cos 3a = cos(2a + a) = cos 2a cos a − sen 2a sen a = (2 cos2 a − 1) cos a − 2 sen2 a cos a = 2 cos3 a − cos a − 2(1 − cos2 a) cos a = 4cos3 a − 3 cos a Temos que cos 3a = 4 cos3 a − 3 cos a 281 CEDERJ
- 284. Transforma¸oes c˜ C´lculo de sen 3a a Sabemos que cos 2a = 1 − 2 sen2 a pois cos 2a = cos2 a − sen2 a e cos2 a = 1 − sen2 a. Logo, sen 3a = sen(2a + a) = sen 2a cos a + sen a cos 2a = 2 sen a cos2 a + (1 − 2 sen2 a) sen a = 2 sen a(1 − sen2 a) + (1 − 2 sen2 a) sen a = 3 sen a − 4 sen3 a Temos que: sen 3a = 3 sen a − 4 sen3 a C´lculo de tg 3a a 2 tg a tg 2a + tg a 1−tg2 a + tg a tg 3a = tg(2a + a) = = 2 tg a 1 − tg 2a tg a 1 − 1−tg2 a tg a 3 3 tg a − tg a = 1 − 3 tg2 a π a = kπ + 3 3 tg a − tg a 2 Da´ tg 3a = ı , e 1 − 3 tg2 a a = kπ + π 6 Arco Metade Consiste em relacionar as fun¸˜es de um arco b com as fun¸˜es do arco co co b . 2 Destacam-se os seguintes casos: b b b Dado cos b, obter cos , sen e tg . 2 2 2 b C´lculo de cos a 2 b Sendo cos 2a = 2 cos2 a − 1, fazendo 2a = b e da´ a = ı temos: 2 b b 1 + cos b cos b = 2cos2 − 1 ⇒ cos = ± 2 2 2 b C´lculo de sen a 2 b Sendo cos 2a = 1 − 2 sen2 a, fazendo 2a = b e da´ a = ı temos: 2 b b 1 − cos b cos b = 1 − 2 sen2 ⇒ sen = ± 2 2 2 CEDERJ 282
- 285. Transforma¸oes c˜ ´ MODULO 1 - AULA 23 b C´lculo de tg a 2 b b sen 2 tg = b 2 cos 2 b 1 − cos b Da´ tg ı 2 =± , b = 2kπ + π, k ∈ Z. 1 + cos b Observa¸˜o: ca Os sinais ± das express˜es s´ tem sentido quando se conhece cos b, sem o o conhecer b. b Dado tg = t, obter sen b, cos b e tg b 2 C´lculo de tg b a 2 tg a b tg 2a = 2 , fazendo 2a = b ⇒ a = . 1 − tg a 2 b = kπ + π b 2 tg 2 2t 2t 2 Logo, tg b = b = ⇒ tg b = ; e (k ∈ Z) 1 − tg2 2 1 − t2 1 − t2 b = 2kπ + π C´lculo de sen b a b Sendo sen 2a = 2 sen a cos a, fazendo 2a = b e portanto a = , con- 2 b b ımos que sen b = 2 sen cos ; clu´ 2 2 b b 2 sen 2 cos2 2 sen b = b ; (b = 2kπ + π, k ∈ Z) cos 2 b b 2 tg 2 2 tg 2 sen b = b = b sec2 2 1 + tg2 2 2t Portanto, sen b = ; (b = 2kπ + π, k ∈ Z) 1 + t2 C´lculo de cos b a 2t 1+t2 1 − t2 kπ cos b = 2t = ; b= , k∈Z 1−t2 1 + t2 2 283 CEDERJ
- 286. Transforma¸oes c˜ Exerc´ ıcios Resolvidos √ 5 1. Calcular sen 2a e cos 2a, sendo dado cos a = , a ∈ 1◦ quadrante. 3 Solu¸˜o ca 1◦ ) C´lculo de sen a a √ 2 sen a = + 1 − cos2 a = 3 ◦ 2 ) C´lculo de sen 2a a √ √ 2 5 4 5 sen 2a = 2 sen a cos a = 2 · · = 3 3 9 ◦ 3 ) C´lculo de cos 2a a 4 8 1 cos 2a = 1 − 2 sen2 a = 1 − 2 · = 1 − = 9 9 9 sen 3x + sen3 x kπ 2. Simplificar a express˜o y = a 3 x + cos 3x ,x= , k ∈ Z. cos 2 Solu¸˜o ca 3 sen x − 4 sen3 x + sen3 x 3 sen x − 3 sen3 x y = = cos3 x − (4 cos3 x − 3 cos x) 3 cos x − 3 cos3 x 3 sen x(1 − sen2 x) sen x cos2 x cos x y = 2 x) = 2x = ⇒ y = cotg x 3 cos x(1 − cos cos x sen sen x x 1 3. Calcular cos 2x, sabendo que tg = e x ∈ 4◦ quadrante. 2 3 Solu¸˜o ca tg x = ± 1 − cos x Temos 2 1 + cos x tg x = 1 2 3 2 1 1 − cos x 1 1 − cos x 4 ent˜o = ± a ⇒ = ⇒ cos x = , j´ que a 3 1 + cos x 3 1 + cos x 5 x ∈ 4◦ quadrante. 2 2 4 7 7 Mas cos 2x = 2 cos x − 1 = 2 −1 = ⇒ cos 2x = . 5 25 25 4. Calcular cos 22◦ 30′ Solu¸˜o ca x 1 + cos x Temos que cos =± 2 2 x Fa¸amos c = 22◦ 30′ ⇒ x = 45◦ . 2 √ 1 + cos 45◦ 2+ 2 Ent˜o cos 22◦ 30′ = + a = 2 2 CEDERJ 284
- 287. Transforma¸oes c˜ ´ MODULO 1 - AULA 23 2 sen x 5. Provar que = sec 2x · tg x cos 3x + cos x Solu¸˜o ca De fato, 2 sen x 2 sen x 2 sen x = = cos 3x + cos x 4 cos3 x − 3 cos x + cos x 4 cos3 x − 2 cos x sen x sen x = = 2 cos3 x − cos x cos x(2 cos2 x − 1) sen x = = sec 2x · tg x cos x · cos 2x x 6. Calcular tg , sabendo-se que sen2 x + cos2 x = 1 2 Solu¸˜o ca 2 2 2t 1 − t2 x Sabemos que sen x + cos x = 1 ⇒ 2 + 2 = 1, t = tg . 1+t 1+t 2 Vem: 2t + 1 − t2 = 1 + t2 ⇒ 2t2 − 2t = 0 ⇒ t = 0 ou t = 1. x x Da´ tg = 0 ou tg = 1 ı 2 2 Exerc´ ıcios Propostos 4 1. Se sen a = , calcular: a) sen 2a b) cos 2a 5 1 2. Se sen a − cos a = , calcule sen 2a 5 π 3. Se y = 3 + sen x cos x, 0 ≤ x ≤ . Determine o maior valor que y pode 2 assumir. π π π 14π 4. Calcular y = sen2 − cos2 + tg + tg . 12 12 3 3 5. Se tg x = m e tg 2x = 3m, m > 0. Determine o ˆngulo x. a 1 1 6. Se tg a = e sen b = √ , calcular tg(a + 2b). 7 10 √ ◦ 1+ 5 7. Sabendo que cos 36 = , determine cos 72◦ . 4 8. Se sen x · cos x = 0, 04, determine cotg2 2x. 3 π 9. Sabendo que sen θ = e < θ < π, calcule 5 2 θ A = 25 sen θ + 10 sen 2 6 + 2 cos 4x 10. Simplificar y = em fun¸˜o de tg x = t. ca 1 − cos 4x 285 CEDERJ
- 288. Transforma¸oes c˜ Gabarito 24 7 1. a) sen 2a = ± b) cos 2a = − 25 25 24 2. 25 7 3. 2 √ 3 4. − 2 5. 180◦ k + 30◦ , k ∈ Z 6. 1 √ 5−1 7. 4 9 8. 16 √ 9. 15 + 3 10 1 + t4 10. y = t2 Transforma¸˜o em Produto ca O problema consiste em transformar certas express˜es, que aparecem o soma de fun¸˜es trigonom´tricas de um ou mais arcos, em express˜es onde co e o aparecem apenas produto de fun¸˜es trigonom´tricas dos mesmos arcos de co e outros arcos com eles relacionados. J´ sabemos que a cos(a + b) = cos a cos b − sen a sen b (i) cos(a − b) = cos a cos b + sen a sen b (ii) sen(a + b) = sen a cos b + sen b cos a (iii) sen(a − b) = sen a cos b − sen b cos a (iv) (i)+(ii) cos(a + b) + cos(a − b) = 2 cos a cos b (v) (i)−(ii) cos(a + b) − cos(a − b) = −2 sen a sen b (vi) (iii)+(iv) sen(a + b) + sen(a − b) = 2 sen a cos b (vii) (iii)−(iv) sen(a + b) − sen(a − b) = 2 sen b cos a (viii) As express˜es assim obtidas chamam-se F´rmulas de Revers˜o ou F´rmulas o o a o de Werner. CEDERJ 286
- 289. Transforma¸oes c˜ ´ MODULO 1 - AULA 23 p+q a+b=p a= Fazendo e resolvendo este sistema vem 2 a−b=q p−q b= 2 Das f´rmulas de revers˜o vem: o a p+q p−q cos p + cos q = 2 cos cos (ix) 2 2 p+q p−q cos p − cos q = −2 sen sen (x) 2 2 p+q p−q sen p + sen q = 2 sen cos (xi) 2 2 p+q p−q sen p − sen q = 2 cos sen (xii) 2 2 Temos que sen p sen q sen p cos q ± cos p sen q tg p ± tg q = ± = cos p cos q cos p · cos q Da´ ı sen(p + q) tg p + tg q = (xiii) cos p cos q sen(p − q) tg p − tg q = (xiv) cos p cos q De forma similar temos: sen(p + q) cotg p + cotg q = (xv) sen p · sen q sen(p − q) cotg p − cotg q = − (xvi) sen p · sen q As f´rmulas de (ix) a (xvi) chamam-se F´rmulas de Transforma¸˜es em o o co Produto ou F´rmulas de Prostaf´rese. o e Exerc´ ıcios Resolvidos 1. Transformar em produto: sen p − cos p Solu¸˜o ca π p+ π −p 2 p− π −p 2 sen p − cos p = sen p − sen − p = 2 cos sen 2 2 2 √ π 2p − π 2 2 π √ π = 2 cos · sen =2 · sen p − = 2 sen p − 4 2 2 4 4 287 CEDERJ
- 290. Transforma¸oes c˜ 2. Transformar em produto: 1 + tg a Solu¸˜o ca √ π sen π + a 4 2 sen π + a 2 sen π + a 1+tg a = tg +tg a = = √ 4 = 4 4 cos π cos a 4 2 cos a cos a 7π 5π 3. Calcular o valor da express˜o y = 2 sen a · cos . 12 12 Solu¸˜o ca Como 2 sen a sen b = sen(a + b) + sen(a − b) 7π 5π 7π 5π 7π 5π y = 2 sen cos = sen + + sen − 12 12 12 12 12 12 π 1 1 = sen π + sen = 0 + = 6 2 2 1 Logo, y = 2 sen 2x + sen 4x 4. Simplificar y = cos 2x − cos 4x Solu¸˜o ca sen 2x + sen 4x 2 sen 2x+4x cos 2x−4x 2 2 y= = cos 2x − cos 4x −2 sen 2x+4x sen 2x−4x 2 2 2 sen 3x cos(−x) 2 sen 3x cos x y= = = cotg x −2 sen 3x sen(−x) 2 sen 3x sen x ⇒ y = cotg x 5. Determine a soma sen 75◦ − cos 75◦ Solu¸˜o ca 75◦ + 15◦ 75◦ − 15◦ sen 75◦ − cos 75◦ = sen 75◦ − sen 15◦ = 2 cos sen √ √ 2 2 ◦ ◦ 2 1 2 = 2 cos 45 · sen 30 = 2 · · = 2 2 2 Exerc´ ıcios Propostos cos 6x + cos 4x 1. Simplificar y = sen 6x − sen 4x 2. Calcular y = cos 20◦ · cos 40◦ · cos 80◦ cos(a − 3b) − cos(3a − b) 3. Simplificar sen 2a + sen 2b 4. Transformar em produto: y = sen 3x + sen x π 8π 5. Calcular y = cos · cos 12 12 CEDERJ 288
- 291. Transforma¸oes c˜ ´ MODULO 1 - AULA 23 π π 6. Se a e b s˜o ˆngulos complementares, 0 < a < , 0 < b < a a e 2 2 sen a + sen b √ 3a = 3, determine sen + cos 3b sen a − sen b 5 7. Transformar em produto: y = sen2 x − sen2 3x 8. Calcular y = tg 9◦ − tg 27◦ − tg 63◦ + tg 81◦ Gabarito 1. y = cotg x 1 2. y = 8 3. 2 sen(a − b) 4. y = 2 sen 2x · cos x √ √ 2+ 6 5. − 8 √ 6. 2 7. y = − sen 2x · sen 4x 8. y = 4 289 CEDERJ
- 293. Equa¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 24 Aula 24 – Equa¸˜es Trigonom´tricas co e Equa¸˜es Fundamentais co Considere f e g duas fun¸˜es trigonom´tricas. Resolver a equa¸˜o tri- co e ca gonom´trica f (x) = g(x) significa determinar o conjunto S, denominado e conjunto solu¸˜o dos n´ meros r para os quais f (r) = g(r) ´ uma senten¸a ca u e c verdadeira. Quase todas as equa¸˜es trigonom´tricas reduzem-se a uma das trˆs co e e equa¸˜es seguintes: co 1a ) sen a = sen b 2a ) cos a = cos b 3a ) tg a = tg b denominadas, por este motivo, equa¸˜es fundamentais. co Equa¸˜o do tipo sen α = sen β ca Se sen α = sen β = OP1 , ent˜o as imagens de α e β no ciclo est˜o sobre a a a reta r que ´ perpendicular ao eixo dos senos no ponto P1 , isto ´, est˜o em e e a ′ P ou P . P′ P1 P r ou O O P1 r P P′ H´, portanto, duas possibilidades: a 1a ) α e β tˆm a mesma imagem, isto ´, s˜o cˆngruos. e e a o 2a ) α e β tˆm imagens sim´tricas em rela¸˜o ao eixo dos senos, isto ´, e e ca e s˜o suplementares. a Portanto α = β + 2kπ sen α = sen β ⇔ ou , k∈Z α = π − β + 2kπ 291 CEDERJ
- 294. Equa¸oes Trigonom´tricas c˜ e Exerc´ ıcios Resolvidos 1. Resolver as seguintes equa¸˜es em R. co π a) sen x = sen 10 b) csc x = −2 c) sen 3x = 1 Solu¸˜o ca π x= + 2kπ π 10 a) sen x = sen ⇒ ou 10 x = π − π + 2kπ 10 Temos a solu¸˜o ca π 9π S= x∈R|x= + 2kπ ou x = + 2kπ, k ∈ Z 10 10 b) csc x = −2 x = 7π + 2kπ 6 1 1 7π = −2 ⇒ sen x = − = sen ⇒ ou sen x 2 6 x = π − 7π + 2kπ 6 Da´ a solu¸˜o ı ca 7π π S= x∈R|x= + 2kπ ou x = − + 2kπ, k ∈ Z 6 6 π π π 2kπ c) sen 3x = 1 = sen ⇒ 3x = + 2kπ ⇒ x = + 2 2 6 3 A solu¸˜o ´ ca e π 2kπ S= x∈R|x= + , k∈Z 6 3 2. Determine os valores de x ∈ R, que satisfazem a equa¸˜o 4 sen4 x − ca 2 11 sen x + 6 = 0. Solu¸˜o ca 4 sen4 x − 11 sen2 x + 6 = 0 Considere sen2 x = y, temos: 4y 2 − 11y + 6 = 0 √ 11 ± 121 − 96 2 y= ⇒y= 3 8 4 √ Se y = sen2 x = 2 ⇒ y = ± 2 (Falso, j´ que −1 ≤ sen x ≤ 1) a √ 3 3 y = sen2 x = ⇒ sen x = ± 4 2 CEDERJ 292
- 295. Equa¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 24 √ 3 Resolvendo sen x = ± , vem: 2 x = 2kπ + π √ 3 3 π sen x = ⇒ sen x = sen ⇒ ou 2 3 x = 2kπ + π − π = 2kπ − 2π 3 3 x = 2kπ + 4π √ 3 4π 3 sen x = − ⇒ sen x = sen ⇒ ou 2 3 x = 2kπ + π − 4π = 2kπ − π 3 3 Podemos escrever ent˜o que a solu¸˜o S ´: a ca e π S = x ∈ R | x = kπ ± , k ∈ Z 3 Equa¸˜o do Tipo cos a = cos b ca Se cos α = cos β = OP2 , ent˜o as imagens de α e β no ciclo est˜o sobre a a a reta r que ´ perpendicular ao eixo dos cossenos no ponto P2 , isto ´, est˜o e e a ′ em P ou P . r r P P A A A′ P2 ou A′ O P2 O P′ P′ H´ portanto duas possibilidades: a 1a ) α e β tˆm a mesma imagem, isto ´, s˜o cˆngruos. e e a o 2a ) α e β tˆm imagens sim´tricas em rela¸˜o ao eixo dos cossenos, isto e e ca ´, s˜o replementares. e a Portanto α = β + 2kπ cos α = cos β ⇔ ou , k∈Z α = −β + 2kπ 293 CEDERJ
- 296. Equa¸oes Trigonom´tricas c˜ e Exerc´ ıcios Resolvidos 1. Resolver as seguintes equa¸˜es em R co π a) cos x = cos 20 2π b) sec x = sec 3 c) cos 4x = −1 Solu¸˜o ca π π a) cos x = cos ⇒ x = 2kπ ± 20 20 π S = x ∈ R | x = 2kπ ± , k∈Z 20 2π 1 1 2π b) sec x = sec ⇒ = 2π ⇒ cos x = cos 3 cos x cos 3 3 2π S= x ∈ R | x = 2kπ ± , k∈Z 3 kπ π c) cos 4x = −1 ⇒ 4x = 2kπ + π ⇒ x = + 2 4 kπ π S= x∈R|x= + , k∈Z 2 4 2. Resolver a equa¸˜o 2 − 2 cos x = sen x · tg x em R ca Solu¸˜o ca 2 − 2 cos x = sen x · tg x sen x 2 − 2 cos x = sen x · ⇒ 2 cos x − 2 cos2 x = sen2 x cos x ⇒ 2 cos x − 2 cos2 x = 1 − cos2 x ⇒ cos2 x − 2 cos x + 1 = 0 √ 2± 4−4 1 cos x = ⇒ cos x = Logo, x = 2kπ. 2 1 S = {x ∈ R | x = 2kπ, k ∈ Z} CEDERJ 294
- 297. Equa¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 24 Equa¸˜o do tipo tg α = tg β ca Se tg α = tg β = AT , ent˜o as imagens de α e β est˜o sobre a reta r a a determinada por O e T , isto ´, est˜o em P ou P ′ . e a T P P A ou O A O P′ P′ r T r H´, portanto, duas possibilidades: a 1a ) α e β tˆm a mesma imagem, isto ´, s˜o cˆngruos. e e a o 2a ) α e β tˆm imagens sim´tricas em rela¸˜o ao centro do ciclo, isto ´, e e ca e s˜o explementares. a Portanto α = β + 2kπ tg α = tg β ⇔ ou ⇔ α = β + kπ, k ∈ Z α = π + β + 2kπ Exerc´ ıcios Resolvidos 1. Resolver as seguintes equa¸˜es: co a) tg 5x = tg 4x b) tg 3x = 1 √ c) tg 4x = − 3 Solu¸˜o ca a) tg 5x = tg 4x ⇒ 5x = 4x + kπ ⇒ x = kπ S = {x ∈ R | x = kπ, k ∈ Z} π π π kπ b) tg 3x = 1 = tg ⇒ 3x = + kπ ⇒ x = + 4 4 12 3 kπ π S= x∈R|x= + , k∈Z 3 12 √ 2π 2π π kπ c) tg 4x = − 3 ⇒ tg 4x = tg ⇒ 4x = + kπ ⇒ x = + 3 3 6 4 kπ π S= x∈R|x= + , k∈Z 4 6 295 CEDERJ
- 298. Equa¸oes Trigonom´tricas c˜ e 2. Resolver a equa¸˜o sec2 x = 1 + tg x. ca Solu¸˜o ca sec2 x = 1 + tg x ⇒ 1 + tg2 x = 1 + tg x ⇒ tg2 x − tg x = 0 ⇒ tg x(tg x − 1) = 0 ⇒ tg x = 0 ou tg x = 1 π S = x ∈ R | x = kπ ou x = kπ + , k∈Z 4 Solu¸˜es de uma equa¸˜o dentro de um certo intervalo co ca Quando tivermos resolvendo uma equa¸˜o pertencente a um determi- ca nado intervalo I devemos fazer o seguinte procedimento: 1◦ ) Resolvemos normalmente a equa¸˜o, n˜o tomando conhecimento do ca a intervalo I at´ obtermos a solu¸˜o geral. e ca 2◦ ) Obtida a solu¸˜o geral, atribu´ ca ımos a k ∈ Z todos os valores inteiros que acarretem as solu¸˜es estarem em I. co Exerc´ ıcios Resolvidos 1 1. Determinar x ∈ [0, 2π] tal que sen 4x = 2 Solu¸˜o ca 1 sen 4x = , x ∈ [0, 2π] 2 π x = π + 2kπ 4x = + 2kπ π 6 24 4 sen 4x = sen ⇒ ou ⇒ ou 6 4x = π − π + 2kπ x = 5π + 2kπ 6 24 4 Vamos calcular as solu¸˜es que pertencem ao intervalo [0, 2π] co π 5π 37π 41π k = 0 ⇒ x1 = , x2 = k = 3 ⇒ x7 = , x8 = 24 24 24 24 13π 17π 49π 53π k = 1 ⇒ x3 = , x4 = k = 4 vamos achar e 24 24 24 24 25π 29π k = 2 ⇒ x5 = , x6 = Estas solu¸˜es n˜o pertencem ao co a 24 24 intervalo fechado de 0 a π. π 5π 13π 17π 25π 29π 37π 41π S= , , , , , , , 24 24 24 24 24 24 24 24 CEDERJ 296
- 299. Equa¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 24 2. Achar as solu¸˜es de tg 6x = tg 2x para 0 ≤ x ≤ 2π. co Solu¸˜o ca tg 6x = tg 2x, x ∈ [0, 2π] kπ ⇒ 6x = 2x + kπ ⇒ 4x = kπ ⇒ x = 4 3π 3π k=0⇒x=0 k=3⇒x= k=6⇒x= 4 2 π 7π k=1⇒x= k=4⇒x=π k=7⇒x= 4 4 π 5π k=2⇒x= k=5⇒x= k = 8 ⇒ x = 2π 2 4 π 3π 5π 7π Excluindo os valores , , , para os quais n˜o existem as a 4 4 4 4 tangentes de 6x e 2x, vem: π 3π S= 0, , π, , 2π 2 2 3. Encontre a soma das ra´ da equa¸˜o cos 2x = 0 no intervalo [0, π]. ızes ca Solu¸˜o ca cos 2x = 0 Temos que cos 2x = cos2 x − sen2 x. Da´ cos2 x − sen2 x = 0 ⇒ cos 2x = 0 ı π π Portanto, 2x = 2kπ ± ⇒ x = kπ ± (Solu¸˜o Geral). ca 2 4 No intervalo [0, π] temos as solu¸˜es: co π π k = 0 ⇒ x = 0π + = 4 4 π 3π k=1⇒x=π− = 4 4 π 3π Assim, a soma das ra´ ´ + ızes e =π 4 4 Equa¸˜es Cl´ssicas co a Sugest˜es para resolver a equa¸˜o: a sen x + b cos x = c (a, b, c ∈ R∗ ) o ca M´todo 1 e Fazer mudan¸a de vari´vel c a au + bv = c sen x = u e cos x = v e resolvemos o sistema u2 + v 2 = 1 Calculando u e v, determinamos os poss´ ıveis valores de x. 297 CEDERJ
- 300. Equa¸oes Trigonom´tricas c˜ e M´todo 2 e b Fazendo = tg θ, temos: a b c c a sen x + b cos x = c ⇒ sen x + cos x = ⇒ sen x + tg θ cos x = a a a sen θ c c ⇒ sen x + · cos x = ⇒ sen x cos θ + sen θ cos x = cos θ cos θ a a c ⇒ sen(x + θ) = cos θ, e da´ calculamos x + θ. ı a M´todo 3 e x 2t 1 − t2 Fazendo tg = t, temos sen x = e cos x = , ent˜o: a 2 1 + t2 1 + t2 2t 1 − t2 a sen x+b cos x = c ⇒ a· +b = c ⇒ 2at+b−bt2 = c+ct2 1 + t2 1 + t2 ⇒ (c + b)t2 − 2at + c − b = 0 e reca´ ımos em uma equa¸˜o de 2o grau ca em t. Observe que este m´todo falha se π + 2kπ for solu¸˜o da equa¸˜o, caso e ca ca π em que a substitui¸˜o tg = t n˜o tem sentido. ca a 2 Exerc´ ıcio Resolvido √ 1. Resolver a equa¸˜o 3 cos x + ca 3 sen x = 3. Solu¸˜o ca Vamos resolver esse exerc´ pelos trˆs m´todos. ıcio e e M´todo 1 e Fazendo sen x = u e cos x = v, temos: √ 3v + 3u = 3 (1) u2 + v 2 = 1 (2) 3 − 3v √ √ De (1) vem: u = √ = 3 − 3v (3) 3 √ √ Substituindo (3) em (2) vem: ( 3 − 3v)2 + v 2 = 1 3 − 6v + 3v 2 + v 2 = 1 ⇒ 4v 2 − 6v + 2 = 0 ⇒ 2v 2 − 3v + 1 = 0 √ 3± 9−8 1 v= ⇒v= 1 4 2 √ 3 Portanto, u = 0 ou u = 2 Existem, assim, duas possibilidades: cos x = 1, sen x = 0 ⇒ x = 2kπ ou √ 1 3 π cos x = , sen x = ⇒ x = 2kπ + 2 2 3 π S = x ∈ R | x = 2kπ ou x = 2kπ + , k ∈ Z 298 3 CEDERJ
- 301. Equa¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 24 M´todo 2 e √ √ 3 3 cos x+ 3 sen x = 3 ⇒ cos x+ sen x = 1 ⇒ cos x+tg 30o sen x = 1 3 sen 30o ⇒ cos x + sen x = 1 ⇒ cos 30o cos x + sen 30o sen x = cos 30o cos 30o √ √ o 3 o 3 ⇒ cos(30 − x) = ⇒ cos(x − 30 ) = 2 2 ⇒ x − 30o = 360o k ± 30o x − 30o = 360ok + 30o ⇒ x = 360o k + 60o ou x − 30o = 360ok − 30o ⇒ x = 360ok π S = x ∈ R | x = 2kπ ou x = 2kπ + , k∈Z 3 M´todo 3 e x 2t 1 − t2 Fazendo tg = t, sabemos que sen x = e cos x = , ent˜o: a 2 1 + t2 1 + t2 √ 1 − t2 √ 2t 3 cos x + 3 sen x = 3 ⇒ 3 2 + 3· =3 1+t 1 + t2 √ √ ⇒ 3(1 − t2 ) + 2 3t = 3 + 3t2 ⇒ 3 − 3t2 + 2 3t = 3 + 3t2 √ √ 3 6t2 − 2 3t = 0 ⇒ t = 0 ou t = 3 x x Se tg = 0 ⇒ = kπ ⇒ x = 2kπ 2 2 √ x 3 x π π Se tg = ⇒ = kπ + ⇒ x = 2kπ + 2 3 2 6 3 x S = x ∈ R | x = 2kπ ou x = 2kπ + , k ∈ Z 3 Sugest˜o para resolver as equa¸˜es a co m m sen fi (x) = 0 ou cos fi (x) = 0 i=1 i=1 O m´todo de resolu¸˜o consiste em transformar a soma em produto e e ca estudar as possibilidades do anulamento de cada fator. 1. Resolver as equa¸˜es em R co a) sen 7x + sen 5x = 0 b) cos 6x + cos 4x = 0 299 CEDERJ
- 302. Equa¸oes Trigonom´tricas c˜ e Solu¸˜o ca a) sen 7x + sen 5x = 0 ⇒ 2 sen 6x · cos x = 0 ⇒ sen 6x = 0 ou cos x = 0. kπ Se sen 6x = 0 ⇒ 6x = kπ ⇒ x = 6 π Se cos x = 0 ⇒ x = kπ + 2 kπ π S= x∈R|x= ou x = kπ + , k ∈ Z 6 2 b) cos 6x + cos 4x = 0 ⇒ 2 cos 5x · cos x = 0 ⇒ cos 5x = 0 ou cos x = 0. π kπ π Se cos 5x = 0 ⇒ 5x = kπ + ⇒ x = + 2 5 10 π Se cos x = 0 ⇒ x = kπ + 2 kπ π π S= x∈R|x= + ou x = kπ + , k ∈ Z 5 10 2 2. Calcular x ∈ R tal que sen x + sen 3x + sen 5x = 0. Solu¸˜o ca Vamos transformar sen x + sen 5x em produto sen x + sen 5x = 2 sen 3x cos 2x Da´ sen x + sen 3x + sen 5x = 0 ⇒ 2 sen 3x cos 2x + sen 3x = 0 ı ⇒ sen 3x(2 cos 2x + 1) = 0 ⇒ sen 3x = 0 ou 2 cos 2x + 1 = 0 kπ Se sen 3x = 0 ⇒ 3x = kπ ⇒ x = 3 1 π (2k + 1)π π Se cos 2x = − ⇒ 2x = (2k + 1)π ± ⇒ x = ± 2 6 2 12 kπ (2k + 1)π π S= x∈R|x= ou x = ± , k∈Z 3 2 12 Sugest˜o para resolver a equa¸˜o do tipo sen4 x + cos4 x = a (a ∈ R) a ca sen2 2x Vamos usar a identidade sen4 x + cos4 x = 1 − (∗) 2 Vamos provar (∗) sen4 x + cos4 x = (sen2 x + cos2 x)2 − 2 sen2 x cos2 x 2 sen 2x sen2 2x =1−2 =1− 2 2 CEDERJ 300
- 303. Equa¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 24 Temos ent˜o: a sen2 (2x) sen4 x + cos4 x = a ⇒ 1 − = a ⇒ sen2 2x = 2 − 2a = 2(1 − a) 2 1 S´ existe solu¸˜o se 0 ≤ 2(1 − a) ≤ 1, ou seja, o ca ≤ a ≤ 1. 2 Exerc´ ıcio Resolvido 1 1. Resolver a equa¸˜o sen4 x + cos4 x = ca 2 Solu¸˜o ca 1 Temos que sen2 2x = 2 1 − = 1. Portanto, sen 2x = ±1. Ent˜o a 2 π π 2x = 2kπ ± ⇒ x = kπ ± 2 4 π S = x ∈ R | x = kπ ± , k∈Z 4 Sugest˜o para resolver a equa¸˜o do tipo sen6 x + cos6 x = a (a ∈ R) a ca 3 sen2 2x Vamos usar a identidade sen6 x + cos6 x = 1 − (∗∗) 4 Vamos provar (∗∗) sen6 x + cos6 x = (sen2 x + cos2 x)(sen4 x − sen2 x cos2 x + cos4 x) = sen2 2x sen2 2x 3 sen2 2x = sen4 x + cos4 x − sen2 x cos2 x = 1 − − =1− 2 4 4 Temos ent˜o a 6 6 3 sen2 2x 4 − 4a sen x + cos x = a ⇒ 1 − = a ⇒ sen2 2x = 4 3 4 − 4a 1 Note que s´ existe rela¸˜o se 0 ≤ o ca ≤ 1, ou seja, ≤ a ≤ 1. 3 4 Exerc´ ıcio Resolvido 5 1. Resolver a equa¸˜o sen6 x + cos6 x = ca 8 Solu¸˜o ca 4 4 5 4 3 1 Temos que sen2 2x = (1 − a) = 1− = · = . 3 3 8 3 8 2 √ 2 π Portanto, sen 2x = ± . Ent˜o 2x = kπ ± a 2 4 kπ π S= x∈R|x= ± , k∈Z 2 8 301 CEDERJ
- 304. Equa¸oes Trigonom´tricas c˜ e Exerc´ ıcios Propostos 1. Resolva as seguintes equa¸˜es trigonom´tricas: co e a) sec x = 2 c) sen(π − x) = 0 √ 1 π 3 b) sen x = − d) tg 2x + = 2 6 3 2. Calcule x ∈ R nas equa¸˜es trigonom´tricas: co e a) sec x = cos x √ b) cos x = 3 sen x 3. Resolva as seguintes equa¸˜es: co a) sen x + sen 2x = 0 b) cos2 x · tg x = sen x c) cos 2x − cos2 x = −1 d) cotg x + tg x = sec x · csc x e) tg4 x − 4 tg2 x + 3 = 0 f) cos 2x = 3 sen x + 2 4. Achar as solu¸˜es de sen x − cos x = 1 para 0 ≤ x ≤ 2π. co 5. Resolva a equa¸˜o 2sen x = (4sen x )cos x , sabendo que 0o < x < 360o . ca 6. Determine as solu¸˜es da equa¸˜o sen4 x + cos4 x = 1, satisfazendo a co ca condi¸˜o 0 ≤ x ≤ 2π. ca ızes da equa¸˜o sen2 x + 7. Sendo 0 ≤ x ≤ 2π, determine a soma das ra´ ca sen(−x) = 0. 8. Resolva as seguintes equa¸˜es em R: co a) sen x + sen 3x + sen 4x + sen 6x = 0 b) sen 7x + cos 3x = cos 5x − sen x π π 9. Resolva a equa¸˜o sen x + ca − sen x − = 2 em R. 4 4 10. Resolva as seguintes equa¸˜es: co 3 a) cos x + cos2 x = , −π < x < π 4 π b) sen x + sen2 x + sen3 x + · · · = 1, 0 < x < 2 CEDERJ 302
- 305. Equa¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 24 Gabarito π 1. a) S = x ∈ R | x = 2kπ ± , k∈Z 3 4π π b) S = x ∈ R | x = 2kπ + ou x = 2kπ − , k ∈ Z 3 3 c) S = {x ∈ R | x = π(1 − k), k ∈ Z} kπ d) S = x∈R|x= , k∈Z 2 2. a) S = {x ∈ R | x = kπ, k ∈ Z} π b) S = x ∈ R | x = kπ + , k ∈ Z 6 π 3. a) S = x ∈ R | x = kπ ou x = (2k + 1)π ± , k∈Z 3 b) S = {x ∈ R | x = 2kπ, k ∈ Z} π c) S = x ∈ R | x = kπ + , k ∈ Z 2 kπ d) S = x ∈ R | x = , k∈Z 2 π e) S = x ∈ R | x = kπ ± , k ∈ Z 6 π π f) S = x ∈ R | x = 2kπ − ou x = kπ − (−1)k , k ∈ Z 2 6 π 3π 4. S = , π, 2 2 5. S = {60o , 180o , 300o } 6. S = {0, π, 2π} 7π 7. 2 π (2k + 1) 8. a) S = x ∈ R | x = 2kπ ± ou x = − π, k ∈ Z 2 3 kπ kπ π b) S = x∈R|x= ou x = − , k∈Z 4 2 8 9. ∅ π π 10. a) S = − , 3 3 π b) 6 303 CEDERJ
- 307. Fun¸oes Circulares Inversas c˜ ´ MODULO 1 - AULA 25 Aula 25 – Fun¸˜es Circulares Inversas co Fun¸˜o Arco-Seno ca A fun¸˜o seno, isto ´, f : R → R tal que f (x) = sen x n˜o ´ sobrejetora, ca e a e pois n˜o existe x ∈ R tal que sen x = 2, ou seja f (x) = 2. a π 3π π 3π A fun¸˜o seno n˜o ´ injetora, pois = ca a e e sen = sen , ou seja, 4 4 4 4 π 3π π 3π f =f e = . 4 4 4 4 Para acharmos a fun¸˜o inversa da fun¸˜o seno, esta deve ser bijetora. ca ca π π Consideremos ent˜o a fun¸˜o seno restrita ao intervalo − , a ca e com 2 2 π π contradom´ [−1, 1], ou seja, g : − , ınio → [−1, 1] tal que g(x) = sen x. 2 2 sen x 1 −π −π 2 π 2 π x −1 Note que : π π (1) g ´ sobrejetora, j´ que ∀y, y ∈ [−1, 1], existe x ∈ − , e a tal que 2 2 sen x = y π π (2) g ´ injetora, j´ que no intervalo − , e a se x1 = x2 ⇒ sen x1 = sen x2 . 2 2 Logo de (1) e (2) g ´ bijetora, da´ g admite inversa que vamos denotar e ı −1 por g e vamos denominar de arco-seno. π π g −1 tem dom´ ınio [−1, 1], contradom´ ınio − , e associa a cada 2 2 π π x ∈ [−1, 1], ∃y ∈ − , tal que y = arcsen x. 2 2 π π Portanto y = arcsen x ⇔ sen y = x e − ≤ y ≤ 2 2 Gr´fico da fun¸˜o arco-seno a ca Temos que os gr´ficos de duas fun¸˜es inversas entre si s˜o sim´tricas a co a e ◦ ◦ em rela¸˜o ` reta que cont´m as bissetrizes do 1 e 3 quadrantes. ca a e 305 CEDERJ
- 308. Fun¸oes Circulares Inversas c˜ Gr´fico de g(x) = sen x a Gr´fico de g −1(x) = arcsen x a sen x arcsen x π 1 2 −π 2 −1 O π x O 1 x 2 −1 −π 2 Exerc´ ıcios Resolvidos √ 3 1. Calcular α tal que α = arcsen 2 Solu¸˜o ca √ √ 3 3 π π π Temos α = arcsen ⇔ sen α = e− ≤α≤ ⇒α= 2 2 2 2 3 1 2. Calcular cos arcsen 4 Solu¸˜o ca 1 1 π π Fazendo arcsen = α ⇒ sen α = e − ≤ α ≤ 4 4 2 2 √ √ 1 15 Da´ cos α = 1 − sen2 α = 1 − ı = 16 4 2 12 3. Calcular cos arcsen + arcsen 5 13 Solu¸˜o ca 2 2 π π Considere arcsen = α ⇒ sen α = e − ≤ α ≤ 5 5 2 2 2 √ 2 21 ⇒ cos α = 1− = 5 5 12 12 π π Considere arcsen = β ⇒ sen β = e − ≤ β ≤ ent˜o a 13 13 2 2 144 5 cos β = 1− = 169 13 2 12 Temos que cos arcsen + arcsen = cos(α + β) = cos α cos β − √ 5 13 √ √ 21 5 2 12 21 24 5 21 − 24 sen α sen β = · − · = − = 5 13 5 13 13 65 65 CEDERJ 306
- 309. Fun¸oes Circulares Inversas c˜ ´ MODULO 1 - AULA 25 Fun¸˜o arco-cosseno ca A fun¸˜o cosseno, isto ´, f : R → R tal que f (x) = cos x n˜o ´ ca e a e sobrejetora, pois n˜o existe x ∈ R tal que cos x = 4, ou seja, f (x) = 4. a π 5π π 5π A fun¸˜o cosseno n˜o ´ injetora, pois ca a e = e cos = cos , ou 3 3 3 3 π 5π π 5π seja, f =f e = . 3 3 3 3 Para acharmos a fun¸˜o inversa da fun¸˜o cosseno, esta deve ser bije- ca ca tora. Consideremos ent˜o a fun¸˜o cosseno restrita ao intervalo [0, π] e com a ca ınio [−1, 1], ou seja, g : [0, π] → [−1, 1] tal que g(x) = cos x. contradom´ cos x 1 O π x −1 Note que: (1) g ´ sobrejetora, j´ que ∀y, y ∈ [−1, 1], existe x ∈ [0, π] tal que cos x = y. e a (2) g ´ injetora, j´ que no intervalo [0, π] se x1 = x2 ⇒ cos x1 = cos x2 . e a Logo de (1) e (2) temos que g ´ bijetora, da´ g admite inversa que vamos e ı denotar por g −1 e vamos denominar de arco-cosseno. g −1 tem dom´ ınio [−1, 1], contradom´ ınio [0, π] e associa a cada x ∈ [−1, 1], ∃y ∈ [0, π] tal que y = arccos x. Portanto y = arccos x ⇔ cos y = x e 0 ≤ y ≤ π Gr´fico da fun¸˜o arco-cosseno a ca Temos que os gr´ficos de duas fun¸˜es inversas entre si s˜o sim´tricas a co a e em rela¸˜o ` reta que cont´m as bissetrizes do 1◦ e 3◦ quadrantes. ca a e Gr´fico de g(x) = cos x a Gr´fico de g −1(x) = arccos x a cos x arccos x 1 π O π x −1 −1 1 x 307 CEDERJ
- 310. Fun¸oes Circulares Inversas c˜ Exerc´ ıcios Resolvidos √ 2 1. Calcular α tal que α = arccos . 2 Solu¸˜o ca √ √ 2 2 π Temos que α = arccos ⇒ cos α = e 0 ≤ α ≤ π ent˜o α = a 2 2 4 3 2. Calcular tg arccos . 4 Solu¸˜o ca 3 3 Fazendo arccos = α ⇒ cos α = e 0 ≤ α ≤ π. 4 4 √ 9 7 Da´ sen α = + 1 − ı =+ 16 4 √ 7 √ sen α 7 tg α = = 4 = 3 . cos α 4 3 √ 3 7 Logo tg arccos = tg α = 4 3 7 12 3. Calcular cos arcsen − arccos 25 13 Solu¸˜o ca 7 7 π π Considere arcsen = α ⇒ sen α = e− ≤α≤ . 25 25 2 2 12 12 Considere arccos = β ⇒ cos β = e 0 ≤ β ≤ π. 13 13 49 24 144 5 Temos que cos α = + 1 − =+ e sen β = 1 − = 625 25 169 13 24 12 7 5 323 Da´ cos(α − β) = cos α cos β + sen α sen β = ı · + · = 25 13 25 13 325 7 12 323 Logo cos arcsen − arccos = 25 13 325 Fun¸˜o arco-tangente ca π A fun¸˜o tangente, isto ´, f : ca e x ∈ R | x = kπ + → R tal que 2 π f (x) = tg x ´ sobrejetora, pois ∀y ∈ R, ∃x ∈ R e x = kπ + , k ∈ Z tal que e 2 tg x = y. A fun¸˜o f n˜o ´ injetora, pois 0 = π e tg 0 = tg π. ca a e Para acharmos a fun¸˜o inversa da fun¸˜o tangente, esta deve ser bije- ca ca tora. CEDERJ 308
- 311. Fun¸oes Circulares Inversas c˜ ´ MODULO 1 - AULA 25 π π Consideremos ent˜o a fun¸˜o tangente restrita ao intervalo − , a ca e 2 2 π π com contradom´ ınio R, isto ´, g : − , e → R tal que g(x) = tg x. 2 2 Note que: (1) g ´ sobrejetora e π π (2) g ´ injetora, pois no intervalo − , , a fun¸˜o tangente se x1 , x2 ∈ e ca 2 2 π π − , , x1 = x2 ⇒ tg x1 = tg x2 . 2 2 tg x π −π 2 O 2 π 3π 2 x Logo de (1) e (2) g ´ bijetora, da´ g admite inversa que vamos denotar e ı −1 por g e vamos denominar de arco-tangente. π π g −1 tem dom´ ınio R, contradom´ ınio − , e associa a cada 2 2 π π x ∈ R, ∃y ∈ − , tal que y = arctg x. 2 2 π π Portanto y = arctg x ⇔ tg y = x e − < y < 2 2 Gr´fico da fun¸˜o arco-tangente a ca Temos que os gr´ficos de duas fun¸˜es inversas entre si s˜o sim´tricas a co a e em rela¸˜o ` reta que cont´m as bissetrizes do 1◦ e 3◦ qaudrantes. ca a e Gr´fico de g(x) = tg x a Gr´fico de g −1(x) = arctg x a tg x arctg x π 2 −π 2 O π 2 x O x −π 2 Exerc´ ıcios Resolvidos √ 3 1. Determine α tal que α = arctg 3 Solu¸˜o ca √ √ 3 3 π π Temos que α = arctg ⇔ tg α = e− <α< . 3 3 2 2 π Ent˜o α = a 6 309 CEDERJ
- 312. Fun¸oes Circulares Inversas c˜ 4 1 2. Calcular tg arcsen − arctg 5 4 Solu¸˜o ca 4 4 π π Fazendo arcsen = α ⇒ sen α = e − ≤ α ≤ . 5 5 2 2 √ 4 2α = 16 3 sen α 5 4 Ent˜o cos α = 1 − sen a 1− = e tg α = = 3 = 25 5 cos α 5 3 1 1 π π Fazendo arctg = β ⇒ tg β = e β ∈ − , 4 4 2 2 4 1 tg α − tg β Temos que tg arcsen − arctg = tg(α − β) = = 5 4 1 + tg α tg β 4 3 −14 13 4 1 = 1+ 3 · 4 16 1 1 π 3. Provar a igualdade arctg + arctg = 2 3 4 Solu¸˜o ca 1 1 Consideremos α = arctg , β = arctg 2 3 1 π π Ent˜o tg α = , α ∈ − , a 2 2 2 1 π π tg β = , β ∈ − , 3 2 2 1 1 3+2 tg α + tg β 2 +3 6 5 6 Temos que tg(α + β) = = 1 1 = 1 = · =1 1 − tg α tg β 1− 2 · 3 1− 6 6 5 π Logo α + β = 4 1 1 π Ent˜o, arctg + arctg = a 2 3 4 Exerc´ ıcios Propostos 1 1. Determinar y tal que y = arcsen − 2 √ 1 3 2. Calcular y = sen arcsen + arcsen 2 2 1 3. Encontre a solu¸˜o da equa¸˜o arcsen x = 2 arcsen ca ca 2 √ 2 4. Resolver a equa¸˜o: arcsen x = arccos ca x 4 33π 5. Determine o valor de arcsen cos 5 CEDERJ 310
- 313. Fun¸oes Circulares Inversas c˜ ´ MODULO 1 - AULA 25 12 6. Calcular cos 3 · arcsen 13 1 7 7. Calcular cos · arccos 2 25 1 8. Calcular tg 2 · arctg 5 √ √ π 9. Detemine o n´ mero de solu¸˜es da equa¸˜o arcsen x + arccos x = u co ca 2 10. Calcular y = tg[arcsen(−0, 6)] Gabarito π 1. − 6 2. y = 1 √ 3 3. x = 2 √ 2 3 4. x = 3 π 5. − 10 2035 6. − 2197 4 7. 5 5 8. 12 9. infinitas solu¸˜es co 3 10. − 4 311 CEDERJ
- 315. Inequa¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 26 Aula 26 – Inequa¸˜es Trigonom´tricas co e Os casos mais comuns de inequa¸˜es trigonom´tricas s˜o: co e a 1◦ ) sen x > m 3◦ ) cos x > m 5◦ ) tg x > m , m∈R 2◦ ) sen x < m 4◦ ) cos x < m 6◦ ) tg x < m Esses 6 tipos s˜o denominados inequa¸˜es fundamentais. a co Inequa¸˜o do tipo sen x > m, m ∈ R ca Para resolver inequa¸˜o do tipo sen x > m, procedemos da seguinte ca maneira: marcamos sobre o eixo dos senos o ponto P1 tal que OP1 = m. Tra¸amos por P1 a reta r perpendicular ao eixo dos senos. As imagens dos c n´ meros reais x tais que sen x > m est˜o na interse¸˜o do ciclo com o semi u a ca plano situado acima de r. r P1 x A 0 Determinamos ent˜o os intervalos que x pode pertencer, tomando o cui- a dado de partir de A e percorrer o ciclo no sentido anti-hor´rio at´ completar a e uma volta, descrevendo assim os intervalos que satisfazem o problema. Exerc´ ıcios resolvidos 1 1. Resolver a inequa¸˜o sen x > − ca 2 Solu¸˜o ca Temos que 0 + 2kπ < x < 2kπ + 7π 6 O ≡ 2π ou , k∈Z 11π + 2kπ < x < 2π + 2kπ 7π 1 2 { O 11π 6 6 4 313 CEDERJ
- 316. Inequa¸oes Trigonom´tricas c˜ e Inequa¸˜o do tipo sen x < m, m ∈ R ca Para resolver inequa¸˜o do tipo sen x < m , procedemos da seguinte ca maneira: marcamos sobre o eixo dos senos o ponto P1 , tal que OP1 = m. Tra¸amos por P1 a reta r perpendicular ao eixo dos senos. As imagens dos c n´ meros reais x tais que sen x < m est˜o na interse¸˜o do ciclo com o semi- u a ca plano situado abaixo de r. r P1 x A 0 Determinamos assim os intervalos que x pode pertencer, a partir de A e percorrendo o ciclo no sentido anti-hor´rio at´ completar uma volta. a e Exerc´ ıcios resolvidos √ 2 1. Resolver a inequa¸˜o sen x < ca 2 Solu¸˜o ca Temos que 0 + 2kπ < x < 2kπ + π 3π π 4 4 √ 4 r 3π ou , k∈Z 2{ 2 O ≡ 2π + 2kπ < x < 2π + 2kπ 4 1 2. Resolver a inequa¸˜o | sen x| ≤ ca 2 Solu¸˜o ca 1 1 1 | sen x| ≤ ⇔ − ≤ sen x ≤ 2 2 2 5π π 6 6 1 2 { { O −1 7π 2 11π 6 6 5π 7π 11π S = x ∈ R | 2kπ+ ≤ x ≤ 2kπ+ ou +2kπ ≤ x ≤ 2kπ+2π ou 6 6 6 π 0+2kπ ≤ x ≤ 2kπ+ , k ∈ Z 314 6 CEDERJ
- 317. Inequa¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 26 3. Determinar os valores de x ∈ [0, 2π] tal que sen 3x > 0 Solu¸˜o ca Fazendo 3x = y, temos sen y > 0 ⇒ 2kπ < y < 2kπ + π, k ∈ Z y Como x = , resulta: A 3 2kπ 2kπ π <x< + 3 3 3 Mas x ∈ [0, 2π] ent˜o temos que k = 0 ou k = 1 ou k = 2 a π k=0⇒0<x< 3 ou 2π k=1⇒ <x<π 3 ou 4π 5π k=2⇒ <x< 3 3 π 2π 4π 5π S= x∈R|0<x< ou < x < π ou <x< 3 3 3 3 Inequa¸˜o do tipo cos x > m, m ∈ R ca Este tipo de inequa¸˜o se resolve da seguinte maneira: marcamos sobre ca o eixo dos cossenos o ponto P2 tal que OP2 = m. Tra¸amos por P2 a reta r c perpendicular ao eixo dos cossenos. As imagens dos reais x tais que cos x > m est˜o na interse¸˜o do ciclo com o semi-plano situado ` direita de r. a ca a x A O P2 Para finalizar, descreveremos os intervalos que conv´m ao problema. e 315 CEDERJ
- 318. Inequa¸oes Trigonom´tricas c˜ e Inequa¸˜o do tipo cos x < m, m ∈ R ca Este tipo de inequa¸˜o se resolve da seguinte maneira: marcamos sobre ca o eixo dos cossenos o ponto P2 tal que OP2 tal que OP2 = m. Tra¸amos c por P2 a reta r perpendicular ao eixo dos cossenos. As imagens dos reais x tais que cos x < m est˜o na interse¸˜o do ciclo com o semi-plano situado ` a ca a esquerda de r. x O P2 Para finalizar, descreveremos os intervalos que conv´m ao problema. e Exerc´ ıcios Resolvidos 1 1. Resolver a inequa¸˜o: cos x > ca 2 Solu¸˜o ca O A { 1 O ≡ 2π 2 π 5π Temos que 2kπ ≤ x < 2kπ + ou + 2kπ < x < 2kπ + 2π, k ∈ Z 3 3 √ 2 2. Resolver a inequa¸˜o cos x < − ca 2 Solu¸˜o ca 3π 4 Temos que − √ 2 2 { 3π 5π O 2kπ + < x < 2kπ + , k∈Z 4 4 5π 4 CEDERJ 316
- 319. Inequa¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 26 3. Resolver cos 2x + cos x ≤ 0 Solu¸˜o ca cos 2x + cos x ≤ 0 ⇒ cos2 x − sen2 x + cos x ≤ 0 ⇔ ⇔ 2cos2 x − 1 + cos x ≤ 0 ⇔ 2cos2 x + cos x − 1 ≤ 0 √ −1+3 −1 ± 1+8 2 = −1 cos x = π 4 −1−3 = 1 3 2 2 1 2 π 5π −1 S= x∈R| ≤x≤ O 3 3 5π 3 1 4. Determinar x ∈ [0, 2π] tal que cos 4x ≤ 2 Solu¸˜o ca 1 Considere 4x = y ⇒ cos y ≤ 2 Temos que: π 3 π 5π + 2kπ ≤ y ≤ + 2kπ, k ∈ Z 3 3 y O Como x = , resulta: 4 5π π kπ 5π kπ 3 + ≤x≤ + , k∈Z 12 2 12 2 Mas x ∈ [0, 2π] ent˜o s´ interessam as solu¸˜es em que k = 0 ou k = 1 a o co ou k = 2 ou k = 3 k = 0 ⇒ π ≤ x ≤ 5π 12 12 ou k = 1 ⇒ 7π ≤ x ≤ 11π 12 12 ou k = 2 ⇒ 13π ≤ x ≤ 17π 12 12 ou k = 3 ⇒ 19π ≤ x ≤ 23π 12 12 317 CEDERJ
- 320. Inequa¸oes Trigonom´tricas c˜ e √ 5. Resolver a inequa¸˜o: 2cos x ≤ ca 2 se x ∈ [0, π] π 3 Solu¸˜o ca 1 1 2cos x ≤ 2 2 , como 2 > 1 ⇒ cos x ≤ O 2 π 5π Da´ ı + 2kπ ≤ x ≤ 2kπ + , k ∈ Z 5π 3 3 3 π 5π Como x ∈ [0, π], temos que k = 0 e ser´ ≤ x ≤ π. Note que a > π. 3 3 π S= x∈R| ≤x≤π 3 2cos2 x + cos x − 1 6. Resolver a inequa¸˜o ca > 0 se x ∈ [0, π] cos x − 1 Solu¸˜o ca 2cos2 x + cos x − 1 Considere a inequa¸˜o dada ca > 0 se x ∈ [0, π]. cos x − 1 Seja cos x = a. 2a2 + a − 1 Temos: >0 a−1 √ −1+3 1 2 −1 ± 1+8 4 =2 Resolvendo vem: 2a + a − 1 = 0 ⇒ a = −1−3 4 4 = −1 a−1=0⇒a=1 1 1 Temos ent˜o −1 < a < + ou a > 1, ou seja, −1 < cos x < a ou 2 2 cos x > 1 Mas n˜o existe x ∈ R | cos x > 1 a / 1 Vamos ent˜o resolver a inequa¸˜o: −1 < cos x < a ca 2 π 3 1 2 5π 3 Mas x ∈ [0, π] ent˜o a solu¸˜o no gr´fico ´: a ca a e 1 2 Temos ent˜o que a solu¸˜o ´: a ca e π S= x∈R| <x<π 3 CEDERJ 318
- 321. Inequa¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 26 Inequa¸˜o do tipo tg x > m, m ∈ R ca Este tipo de inequa¸˜o se resolve da seguinte maneira: marcamos sobre ca o eixo das tangentes o ponto T , tal que AT = m. Tra¸amos a reta r = OT . c As imagens das reais x tais que tg x > m est˜o na interse¸˜o do ciclo com o a ca ˆ ˆngulo r Oy. a y T x A O x r Para finalizar, descreveremos os intervalos que conv´m ao problema. e Inequa¸˜o do tipo tg x < m, m ∈ R ca Este tipo de inequa¸˜o se resolve da seguinte maneira: marcams sobre ca o eixo das tangentes o ponto T tal que AT = m. Tra¸amos a reta r = OT . c As imagens das reais x , tais que tg x < m , est˜o na interse¸˜o do ciclo com a ca ˆ o ˆngulo y Or. a y B M T A′ A O M′ r B′ Para finalizar descreveremos os intervalos que conv´m ao problema. e Exerc´ ıcios Resolvidos √ 3 1. Resolver a inequa¸˜o tg x > ca π 3 Solu¸˜o ca 2kπ + π < x < 2kπ + π 2 π 6 T Temos que 6 2 ou , k∈Z A 7π 3π O 2kπ + < x < 2kπ + 6 2 7π 6 que podem ser escritas: 3π 2 π π S = x | kπ + < x < kπ + , k ∈ Z 6 2 319 CEDERJ
- 322. Inequa¸oes Trigonom´tricas c˜ e 2. Resolver a inequa¸˜o tg x < 1 ca Solu¸˜o ca Temos que y r π 4 T A 5π 4 π π 5π S = x ∈ R | 2kπ + 0 ≤ x < 2kπ + ou 2kπ + < x < 2kπ + ou 4 2 4 3π 2kπ + < x < 2kπ + 2π, k ∈ Z 2 √ 3. Resolver a inequa¸˜o | tg x| ≤ 3 ca Solu¸˜o ca √ √ √ | tg x| ≤ 3 ⇒ − 3 ≤ tg x ≤ 3 r Temos ent˜o que: a y π T1 2π 3 3 √ 3 A x √ 4π − 3 5π 3 3 T2 π 2π 4π x ∈ R | 2kπ + 0 ≤ x ≤ 2kπ + ou 2kπ + ≤ x ≤ 2kπ + ou 3 3 3 5π 2kπ + ≤ x < 2kπ + 2π, k ∈ Z 3 √ 4. Determinar x ∈ [0, 2π] tal que 1 ≤ tg 3x < 3 Solu¸˜o ca √ T2 } Considere 3x = y ⇒ 1 ≤ tg y < 3 π √ Temos que: 3 π T1 3 4 } A 1 π π y 5π kπ + ≤ y < kπ + , como x = , vem 4 4π 4 3 3 3 kπ π kπ π + ≤x< + , k∈Z 3 12 3 9 CEDERJ 320
- 323. Inequa¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 26 Mas x ∈ [0, 2π], ent˜o s´ interessam as solu¸˜es em que: k = 0 ou a o co k = 1 ou k = 2 ou k = 3 ou k = 4 ou k = 5. π π k=0⇒ ≤x< 12 9 5π 4π k=1⇒ ≤x< 12 9 9π 7π k=2⇒ ≤x< 12 9 13π 10π k=3⇒ ≤x< 12 9 17π 13π k=4⇒ ≤x< 12 9 21π 16π k=5⇒ ≤x< 12 9 5. Determinar x ∈ [0, π] tal que tg x ≥ −1 Solu¸˜o ca Considere a inequa¸˜o: tg x > −1, x ∈ [0, π] ca 3π 4 A 3π 5π 4 } 1 −1 2 π 3π Note que x ∈ [0, π] ⇒ x∈R|0≤x< ou ≤x≤π 2 4 Exerc´ ıcios Propostos 1. Resolver as inequa¸˜es abaixo: co a) senx ≥ 0 √ 2 b) | sen x| > 2 √ 3 1 c) − ≤ cos x ≤ 2 2 5 d) | cos x| > 3 √ 3 2. Resolver a inequa¸˜o sen 3x ≤ ca se x ∈ [0, 2π]. 2 3. Para que valores de x ∈ R existe log2 (2 sen x − 1)? 321 CEDERJ
- 324. Inequa¸oes Trigonom´tricas c˜ e 4. Resolver a inequa¸˜o em R, sen x + cos x < 1. ca cos x 5. Determinar x ∈ [0, 2π] tal que ≤ 1. cos 2x 4sen2 x − 1 6. Determinar no conjunto dos n´ meros reais o dom´ de y = u ınio , cos x 0 ≤ x ≤ 2π. √ √ 3 7. Resolver a inequa¸˜o em R, − 3 < tg x ≤ ca . 3 8. Resolver a inequa¸˜o tg2 2x ≤ tg 2x, x ∈ [0, 2π]. ca 9. Resolver a inequa¸˜o sen x > cos x, x ∈ [0, 2π]. ca √ √ 10. Resolver a inequa¸˜o em R, tg2 x − ( 3 − 1) tg x − 3 < 0. ca 11. Resolver a inequa¸˜o sen2 x < 2 sen x, x ∈ [0, 2π]. ca 1 12. Resolver a inequa¸˜o em R, ca < 2 tg x. cos2 x 13. Resolver a inequa¸˜o | cos x| ≥ sen x, x ∈ [0, 2π]. ca 1 1 14. Para que valores de x ∈ R, sen x > e cos x ≥ . 2 2 15. Resolver a inequa¸˜o | sen x| > | cos x|, x ∈ [0, π]. ca 16. Resolver a inequa¸˜o (sen x + cos x)2 > 1, x ∈ [0, 2π] ca 1 17. Resolver a inequa¸˜o sen 2x · sec2 x − ca ≤ 0, x ∈ [0, 2π]. 3 3 18. Se 0 ≤ α ≤ π , para todo x real, x2 + x + tg α > ent˜o a 4 π a) 0 < α < 4 π π b) < α < 4 2 π 3π c) < α < 2 4 3π d) α = 4 e) n˜o existe α nestas condi¸˜es a co CEDERJ 322
- 325. Inequa¸oes Trigonom´tricas c˜ e ´ MODULO 1 - AULA 26 Gabarito 1. a) {x ∈ R | 2kπ ≤ x ≤ 2kπ + π} π 3π 5π 7π b) x ∈ R | 2kπ + < x < 2kπ + ou 2kπ + < x < 2kπ + 4 4 4 4 π 5π 7π 5π c) x ∈ R | 2kπ + ≤ x ≤ 2kπ + ou 2kπ + ≤ x ≤ 2kπ + 3 6 6 3 d) S = ∅ 2π 7π 8π 12π 14π 2. x ∈ R | ≤ x ≤ ou ≤ x ≤ ou ≤ x ≤ 2π ou 9 9 9 9 9 π 0≤x≤ 9 π 5π 3. x ∈ R | 2kπ + < x < 2kπ + 6 6 π 4. x ∈ R | 2kπ + < x < 2kπ + 2π 2 π 2π 3π 5π 4π 7π 5. x | x = 0 ou <x≤ ou < x< ou ≤x< ou 4 3 4 4 3 4 x = 2π π π 5π 7π 3π 11π 6. x∈R| ≤ x < ou ≤x≤ ou <x≤ 6 2 6 6 2 6 π 2π 7π 7. x ∈ R | 2kπ ≤ x ≤ 2kπ + ou 2kπ + < x ≤ 2kπ + ou 6 3 6 5π + 2kπ < x < 2kπ + π 3 π 9π 3π 13π π 5π 8. x|0≤x≤ ou π ≤ x ≤ ou ≤x≤ ou ≤ x ≤ 8 8 2 8 2 8 π 5π 9. x∈R| <x< 4 4 π π 10. x ∈ R | kπ − < x < kπ + , k ∈ Z 4 3 11. {x ∈ R | 0 < x < π} 12. ∅ π 3π 13. x∈R|0≤x≤ ou ≤ x ≤ 2π 4 4 π π 14. x ∈ R | 2kπ + < x ≤ 2kπ + , k ∈ Z 6 3 323 CEDERJ
- 326. Inequa¸oes Trigonom´tricas c˜ e π 3π 15. x∈R| <x< 4 4 π 16. x∈R|0<x< 2 π 3π 17. x∈R|0≤x< ou π ≤ x < 2 2 18. b CEDERJ 324



































![Fra¸oes
c˜
´
MODULO 1 - AULA 1
Sugest˜es e Solu¸˜es das Atividades Propostas
o co
Atividade 01
Explique de maneira convincente o porque dos n´ meros 1134 e 53172
u
s˜o divis´
a ıveis por 9.
Solu¸˜o:
ca
Vocˆ deve ter se lembrado do crit´rio de divisibilidade por 9, que ´ sim-
e e e
ples: um n´ mero ´ divis´ por 9 se, e somente se, a soma de seus algarismos
u e ıvel
for divis´ por 9. Assim, como 1 + 1 + 3 + 4 = 9, 1134 ´ divis´ por 9.
ıvel e ıvel
Mas, isso ´ convincente? Bem, se vocˆ simplesmente acredita nas regras, n˜o
e e a
h´ mais nada a discutir. No entanto, essa n˜o ´ uma atitude matem´tica
a a e a
muito positiva. Regras s˜o importantes pois s˜o muito uteis em situa¸˜es
a a ´ co
pr´ticas, fazem parte da cultura matem´tica. Mas, ´ fundamental entender
a a e
o porque da regra funcionar. Neste caso, a explica¸˜o ´ simples. Devido ao
ca e
nosso sistema num´rico decimal, 1134 = 1 × 1000 + 1 × 100 + 3 × 10 + 4.
e
Agora, como 1000 = 999 + 1, 100 = 99 + 1 e 10 = 9 + 1, podemos escrever
1134 = 1 × (999 + 1) + 1 × (99 + 1) + 3 × (9 + 1) + 4 =
= [1 × 999 + 1 × 99 + 3 × 9] + [1 + 1 + 3 + 4].
Como o n´ mero [1 × 999 + 1 × 99 + 3 × 9] ´ divis´ por 9, claramente
u e ıvel
1134 ´ divis´ por 9 se, e somente se, 1+1+3+4 ´ divis´ por 9. Repita
e ıvel e ıvel
o racioc´
ınio com o outro n´ mero. Observe que essa explica¸˜o ´ ilustrativa
u ca e
mas n˜o ´ uma demonstra¸˜o do crit´rio de divisibilidade por 9, uma vez que
a e ca e
usamos apenas um exemplo.
Atividade 02
Por que ´ dif´ decompor o n´ mero 97343 em fatores primos?
e ıcil u
Solu¸˜o:
ca
Quanto tempo vocˆ gastou com esse exerc´
e ıcio? Bem, a id´ia aqui ´
e e
colocar a teoria e a pr´tica em contato. A teoria ´ o maravilhoso Teorema
a e
Fundamental da Aritm´tica que afirma que todo natural admite uma unica
e ´
decomposi¸˜o em fatores primos. A pr´tica ´ o ganha-p˜o de muitos ma-
ca a e a
tem´ticos: pode ser muito, muito dif´ decompor um n´ mero em fatores
a ıcil u
primos. Determinar se um dado n´ mero ´ primo ou n˜o j´ ´ uma tarefa
u e a a e
titˆnica. Procure saber sobre os chamados primos de Mersenne e vocˆ ter´
a e a
uma id´ia melhor do que isso quer dizer. Mas, voltemos ` nossa vaca fria:
e a
por que ´ dif´ decompor o n´ mero 97343 em fatores primos?
e ıcil u
33 CEDERJ](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-35-320.jpg)













































![Equa¸˜o do 1o Grau
ca
´
MODULO 1 - AULA 6
Exemplo 3
A idade de uma pessoa ´ o dobro da de outra. H´ cinco anos a soma das
e a
idades das duas pessoas era igual ` idade atual da mais velha. Quais s˜o as
a a
idades atuais das duas pessoas?
Solu¸˜o:
ca
Sejam x a idade da pessoa mais nova. Portanto, 2x a idade da mais
velha. Usando dados de cinco anos atr´s encontramos que
a
x − 5 + 2x − 5 = 2x ⇔ x = 10 e 2x = 20 .
Logo, as idades atuais s˜o 10 anos e 20 anos.
a
Exerc´
ıcios Propostos
1. Resolva em R, a equa¸˜o 3x − 27 = 0.
ca
2. Resolva em R, a equa¸˜o 12 + 4x = 0.
ca
3. Resolva em R, a equa¸˜o x[2x − (3 − x)] − 3 x2 − 1 = 0.
ca
4. Resolva em R, a equa¸˜o 3x + 1 = 3x + 4.
ca
5. Resolva em R, a equa¸˜o 5(x − 1) = 5x − 5.
ca
5x − 1 x 142
6. Resolva em R, a equa¸˜o
ca − = .
2 3 15
4x − 2 1 1 − 4x
7. Resolva em R, a equa¸˜o
ca − =2− .
5 10 2
8. A soma de cinco n´ meros ´
u ımpares e consecutivos ´ 905. Quais s˜o esses
e a
n´ meros?
u
9. A soma de dois n´ meros ´ 200. Ache-os sabendo que a metade de um
u e
3
´ igual a 4 do outro.
e
10. A diferen¸a entre dois n´ meros ´ 18. Somando 4 a ambos, o maior
c u e
torna-se o qu´druplo do menor. Determine os dois n´ meros.
a u
Gabarito
1. V = {9} 6. V = { 23 }
5
2. V = {−3} 7. V = {− 5 }
3
3. V = {1} 8. 177, 179, 181, 183 e 185
4. V =∅ 9. 120 e 80
5. V =R 10. 20 e 2
79 CEDERJ](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-81-320.jpg)



















![Inequa¸˜o do 1o Grau
ca
´
MODULO 1 - AULA 9
Assim, podemos representar graficamente os sinais.
_ 1/2 + +
_ _ 3 +
+ _ +
1
01111111
0000000
1
0
1/2 3
1 1
Note que 2
´ solu¸˜o. Logo, S = {x ∈ R |
e ca 2
≤ x < 3}.
Exerc´
ıcios
1. Resolva as seguintes inequa¸˜es:
co
x+3
a) <0
x+5
x
b) ≤0
−x + 3
x+3
c) <1
x−1
x+5
d) <2
3x − 4
Gabarito
a) {x ∈ R | −5 < x < −3} b) {x ∈ R | x ≤ 0 ou x > 3}
4 13
c) {x ∈ R | x < 1} d) {x ∈ R | x < 3
ou x > 5
}
Inequa¸˜o Potˆncia
ca e
Encerrando nosso breve estudo de inequa¸˜es vamos colocar em desta-
co
que inequa¸˜es do tipo
co
[f (x)]n ≥ 0 , [f (x)]n > 0 , [f (x)]n ≤ 0 ou [f (x)]n < 0 ,
onde f (x) = ax + b, a = 0 e n > 1 ´ um n´ mero natural.
e u
Exemplo 9
Resolver as inequa¸˜es (3x − 6)6 ≥ 0, (3x − 6)6 > 0, (3x − 6)6 < 0
co
6
e (3x − 6) ≤ 0
99 CEDERJ](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-101-320.jpg)

































![Conjuntos
´
MODULO 1 - AULA 12
Representa¸˜o de Conjuntos Num´ricos
ca e
Podemos representar geometricamente os n´ meros reais em uma reta.
u
A cada ponto da reta est´ associado um n´ mero real e a cada n´mero real
a u u
est´ associado um ponto da reta.
a
B O I A IR
-1 0 1 2 2 3
Para fazer a representa¸˜o escolhemos dois pontos O e I da reta e
ca
associamos a eles os n´ meros reais 0 e 1, respectivamente. O segmento de
u
reta OI ´ muito especial. Foi escolhido para ter comprimento 1. Veja a
e
Figura acima. Os n´ meros reais negativos s˜o colocados na reta ` esquerda
u a a
do ponto O e os n´ meros positivos ` direita do ponto zero.
u a
Nesta representa¸˜o, a distˆncia entre os n´ meros inteiros n e n + 1 ´
ca a u e
a mesma distˆncia que entre os n´ meros 0 e 1.
a u
√
Tamb´m, por exemplo, 2 e −π ganharam as posi¸˜es indicadas na
e co
figura acima, em fun¸˜o de que os segmentos de reta OA e OB medem
ca
√
respectivamente, 2 e π.
Na continua¸˜o de nosso estudo vamos usar (na verdade, j´ estamos
ca a
usando) os seguintes s´
ımbolos:
| significa “tal que” ∃ significa “existe”
∧ significa “e” ∨ significa “ou”
⇔ significa “equivalente” ⇒ significa “implica que”
(i) Intervalos de n´ meros reais.
u
Intervalos s˜o subconjuntos dos n´ meros reais determindos por desigualda-
a u
des.
Sendo a ∈ R, b ∈ R e a < b, temos:
Intervalo fechado
{x ∈ R | a ≤ x ≤ b} = [a, b]. Lˆ-se: x pertence a R, tal que x seja igual
e
ou maior que a e igual ou menor que b. [a, b] ´ o conjunto dos n´ meros reais
e u
compreendidos entre a e b, incluindo a e b.
Representamos na reta [a, b] por:
a b
133 CEDERJ](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-135-320.jpg)
![Conjuntos
Exemplo: [5, 8] = {x ∈ R | 5 ≤ x ≤ 8}. x pode ser igual ou maior que 5 e
igual ou menor que 8.
5 8
Note que na figura acima os pontos a e b s˜o representados por um ponto
a
´ uma conven¸˜o que adotamos para significar que a e b pertencem
cheio. E ca
ao intervalo [a, b].
Intervalo aberto
{x ∈ R | a < x < b} = (a, b)
´ o conjunto dos n´ meros reais compreendidos entre a e b, n˜o incluindo a e
e u a
b. Veja a representa¸˜o geom´trica abaixo.
ca e
a b
Note que na figura acima os pontos a e b s˜o representados por pon-
a
´
tos vazados. E uma conven¸˜o para significar que a e b n˜o pertencem ao
ca a
intervalo (a, b).
Exemplo: (5, 8) = {x ∈ R | 5 < x < 8} ´ o conjunto dos n´ meros maiores
e u
que 5 e menores que 8.
5 8
Intervalo aberto ` esquerda e fechado ` direita
a a
{x ∈ R | a < x ≤ b} = (a, b]
´ o conjunto dos n´ meros reais compreendidos entre a e b, n˜o incluindo a e
e u a
incluindo b. Veja a representa¸˜o geom´trica abaixo.
ca e
a b
Exemplo: (5, 8] = {x ∈ R | 5 < x ≤ 8} ´ o conjunto formado pelos n´ meros
e u
maiores que 5 e iguais ou menores que 8.
Intervalo fechado ` esquerda e aberto ` direita
a a
{x ∈ R | a ≤ x < b} = [a, b)
´ o conjunto dos n´ meros reais compreendidos entre a e b incluindo a e n˜o
e u a
incluindo b. Veja a interpreta¸˜o geom´trica abaixo.
ca e
a b
CEDERJ 134](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-136-320.jpg)



![Conjuntos
7. (CONCITEC-72) Seja A um conjunto de 11 elementos. O conjunto Y
de todos os subconjuntos de A tem n elementos. Pode-se concluir que:
a) n = 2.048 b) n = 2.047 c) n = 2.049 d) n = 2.046 e) 2.050
8. (MACK-SP-79) Se A e B s˜o dois conjuntos tais que A ⊂ B e A = ∅,
a
ent˜o
a
a) sempre existe x ∈ A tal que x ∈ B.
/
b) sempre exite x ∈ B tal que x ∈ A.
/
c) se x ∈ B ent˜o x ∈ A.
a
d) se x ∈ B ent˜o x ∈ A.
/ a /
e) A ∩ B = ∅
9. (CESGRANRIO-79) O n´ mero de conjuntos X que satisfazem: {1, 2} ⊂
u
X ⊂ {1, 2, 3, 4} ´:
e
a) 3 b) 4 c) 9 d) 6 e) 7
10. (PUC-RJ-79) O n´ mero de elementos do conjunto A ´ 2m e o n´ mero
u e u
n
de elementos do conjunto B ´ 2 . O n´ mero de elementos de (A × B)
e u
´:
e
a) 2m + 2n b) 2m×n c) 2m+n d) m × n e) m + n
11. (FGV-SP-80) Considere as afirma¸˜es a respeito da parte hachurada
co
do diagrama seguinte:
OBS.: U = A ∪ B ∪ C ´ o conjunto universo e B e C s˜o os comple-
e a
mentares de B e C, respectivamente.
I) A ∩ (B ∪ C) B
A
II) A ∩ (B ∩ C)
III) A ∩ (B ∩ C)
IV) A ∩ (B ∩ C) C
A(s) afirma¸˜o(¸˜es) correta(s) ´ (s˜o):
ca co e a
a) I b) III c) I e IV d) II e III e) II e IV
12. (UFRS-80) Sendo A = {0, 1} e B = {2, 3}, o n´ mero de elementos
u
[P (A) ∩ P (B)] ´:
e
a) 0 b) 1 c) 2 d) 4 e) 8
CEDERJ 138](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-140-320.jpg)
![Conjuntos
´
MODULO 1 - AULA 12
13. Dados A = [1, ∞), B = (−∞, −2) ∪ (1, ∞) e C = [−3, 4], assinale
falso ou verdadeiro
( ) A−B =∅
( ) (A ∪ B) ∩ C = [1, 4]
( ) CR B = [−2, 1]
( ) A ∩ B ∩ C = (1, 4]
14. (ITA) Depois de N dias de f´rias, um estudante observa que:
e
I - Choveu 7 vezes, de manh˜ ou ` tarde.
a a
II - Quando chove de manh˜, n˜o chove ` tarde.
a a a
III - Houve 5 tardes sem chuva.
IV - Houve 6 manh˜s sem chuva.
a
O n´ mero N de dias de f´rias foi:
u e
a) 7 b) 9 c) 10 d) 11 e) 8
Gabarito
1. a) F , b) F , c) V , d) V , e) F , f) F . 2. a) 2 ∈ A, b) 1 ∈ B, c) 3 ⊂ B,
d) A = B. 3. a), c), d), g), h) s˜o verdadeiras. 4. b) 5. c) 6. d) 7. a)
a
8. d) 9. b) 10. c) 11. d) 12. b) 13. F, V, V, V 14 b)
139 CEDERJ](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-141-320.jpg)





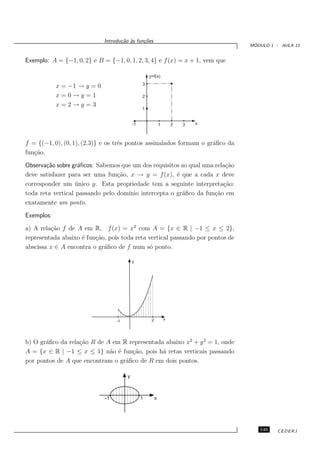






![Introdu¸˜o `s fun¸oes
ca a c˜
9. (PUC-95) Dentre os 4 desenhos a seguir:
y y
x x
I II
y y
x x
III IV
a) Somente I pode ser gr´fico de fun¸˜o da forma y = f (x).
a ca
b) I, III e IV podem ser gr´ficos de fun¸˜es da forma y = f (x).
a co
c) Nenhum deles pode ser gr´fico de fun¸˜es da forma y = f (x).
a co
d) II e IV n˜o podem ser gr´ficos de fun¸˜es da forma y = f (x).
a a co
e) Nenhuma das respostas acima.
10. (UFF-94-1a fase) O gr´fico que melhor representa a fun¸˜o polinomial
¯ a ca
2 4
p(x) = (x − 1) (x − 4)(x + 9 ) ´:
e
A) B)
y y
0 x 0 x
C) D)
y y E)
y
0 x 0 x
x
0
11. Esboce o gr´fico de:
a
a) y = x2 − 1, D = R
b) f (x) = x − 2, sendo D = [−2, 2]
CEDERJ 152](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-154-320.jpg)

![Introdu¸˜o `s fun¸oes
ca a c˜
17. (UERJ/93) A fun¸˜o f definida no conjunto dos inteiros positivos por:
ca
n , se n for par
f (n) = 2
3n + 1, se n for ´ımpar
O n´ mero de solu¸˜es da equa¸˜o f (n) = 25 ´:
u co ca e
a) zero b) um c) dois d) quatro e) infinito
18. (UFC-CE) Qual dos gr´ficos a seguir n˜o pode representar uma fun¸˜o?
a a ca
a) y b) y c) y d) y e) y
19. (FGV-SP) Considere a seguinte fun¸˜o de vari´vel real
ca a
1 se x ´ racional
e
f (x) =
0 se x ´ irracional
e
Podemos afirmar que:
a) f (2, 3) = 0
b) f (3, 1415) = 0
c) 0 ≤ f (a) + f (b) + f (c) ≤ 3
d) f [f (a)] = 0
e) f (0) + f (1) = 1
20. (SANTA CASA-82) Seja f uma fun¸˜o de Z em Z, definida por
ca
0, se x ´ par
e
f (x) =
1, se x ´ ´
e ımpar
Nestas condi¸˜es, pode-se afirmar que:
co
a) f ´ injetora e n˜o sobrejetora
e a
b) f ´ sobrejetora e n˜o injetora
e a
c) f (−5) · f (2) = 1
d) f (f (x)) = 0, ∀ x ∈ R
e) O conjunto-imagem de f ´ {0, 1}
e
CEDERJ 154](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-156-320.jpg)
![Introdu¸˜o `s fun¸oes
ca a c˜
´
MODULO 1 - AULA 13
21. (FUVEST-82) O n´ mero real α ´ solu¸˜o simultˆnea das equa¸˜es
u e ca a co
f (x) = 0 e g(x) = 0 se e somente se α ´ raiz da equa¸˜o:
e ca
a) f (x) + f (x) = 0
b) [f (x)]2 + [g(x)]2 = 0
c) f (x) · g(x) = 0
d) [f (x)]2 − [g(x)]2 = 0
e) f (x) − g(x) = 0
˜ e
22. (PUC-93) Entre as fun¸˜es T : R2 → R2 abaixo, NAO ´ injetora a
co
definida por:
a) T (x, y) = (x, 0)
b) T (x, y) = (y, x)
c) T (x, y) = (2x, 2y)
d) T (x, y) = (−y, x)
e) T (x, y) = (x + 1, y + 1)
Exerc´
ıcios - S´rie B
e
1. (UNIFICADO-92) Qual dos gr´ficos abaixo representa, em R2 as solu¸˜es
a co
2 2
da equa¸˜o y = x(x − 1).
ca
A) B)
C) D) E)
y y
y y y
x x x x x
2. (IBEMEC 98) Considere a fun¸˜o f , de R em R, tal que f (x + 1) =
ca
f (x) + 2 e f (2) = 3. Ent˜o, f (50) ´ igual a:
a e
a) 105 b) 103 c) 101 d) 99 e) 97
3. (FUVEST-SP) Seja f uma fun¸˜o tal que f (x + 3) = x2 + 1 para todo
ca
x real. Ent˜o f (x) ´ igual a:
a e
a) x2 − 2 b) 10 − 3x c) −3x2 + 16x − 20 d) x2 − 6x + 10 e) x2 + 6x − 16
155 CEDERJ](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-157-320.jpg)




![Fun¸oes composta e inversa
c˜
(ii) Suponha Z o conjunto dos n´ meros inteiros, f : Z → Z f (x) = x − 2
u
g: Z → Z g(x) = x3
ent˜o a fun¸˜o composta h : Z → Z pode ser calculada por
a ca
h(x) = g(f (x))
h(x) = g(x − 2)
h(x) = (x − 2)3
Exerc´
ıcios resolvidos
(i) Sejam as fun¸˜es f : R → R e g : R → R definidas por f (x) = x2 − 1 e
co
g(x) = x + 3.
a) obter a fun¸˜o composta h = g ◦ f e m = f ◦ g
ca
b) calcule h(2) e m(−3)
c) existem valores x ∈ R tais que h(x)=0?
Solu¸˜o:
ca
a) h(x) = g(f (x)) = g(x2 − 1) = x2 − 1 + 3
h(x) = x2 + 2
m(x) = f (g(x)) = f (x + 3) = (x + 3)2 − 1
m(x) = x2 + 6x + 9 − 1 = x2 + 6x + 8
b) h(2) = 22 + 2 = 4
m(−3) = (−3)2 + 6(−3) + 8
m(−3) = 9 − 18 + 8 = −1
c) h(x) = 0 ⇔ x2 +2 = 0 (esta equa¸˜o n˜o tem solu¸˜o x ∈ R). Resposta:
ca a ca
N˜o.
a
√
(ii) Sejam f : R → R e g : R → R. Sabendo-se que f (x) = 5 + x2 e que a
√
imagem da fun¸˜o f ◦ g ´ o intervalo real [+ 5, +3], a alternativa que
ca e
representa a imagem da fun¸˜o g ´:
ca e
√
a) [+ 5, +3] b) [−2. + 2]
√ √
c) [−2, + 5] d) [− 5, +2]
√ √
e) [− 5, + 5]
CEDERJ 160](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-162-320.jpg)
![Fun¸oes composta e inversa
c˜
´
MODULO 1 - AULA 14
Solu¸˜o:
ca
g f
Im(fog)
R R V5 3.
R
√
f ◦ g(x) = f (g(x)) = 5 + g 2(x). Logo 5 ≤ 5 + g 2 (x) ≤ 3 ⇒
5 ≤ 5 + g 2(x) ≤ 9
Ent˜o 0 ≤ g 2(x) ≤ 4. Os valores de g(x) que verificam a desigualdade
a
acima s˜o −2 ≤ g(x) ≤ 2.
a
Logo, Im g(x) = [−2, 2]. Resposta b).
(iii) Sejam as fun¸˜es f : R → R e g : R → R definidas por
co
x2 se x ≥ 0
f (x) = g(x) = x − 3.
x se x < 0
Encontre a express˜o que define f ◦ g = h.
a
Solu¸˜o: h(x) = f (g(x)) = f (x − 3).
ca
Em virtude da defini¸˜o de f precisamos saber quando x − 3 ≥ 0 e
ca
quando x − 3 < 0.
Ora x − 3 ≥ 0 ⇔ x ≥ 3 e x − 3 < 0 ⇔ x < 3.
(x − 3)2 se x ≥ 3
Logo h(x) =
x − 3 se x < 3
(iv) Sejam as fun¸˜es reais g(x) = 3x+2 e (f ◦g)(x) = x2 −x+1. Determine
co
a express˜o de f .
a
Solu¸˜o:
ca (f ◦ g)(x) = f (g(x)) = f (3x + 2) = x2 − x + 1
y−2
Fa¸amos agora 3x + 2 = y ⇒ x =
c
3
Logo,
2
y−2 y−2
f (y) = − +1
3 3
y 2 − 4y + 4 y − 2
f (y) = − +1
9 3
1
f (y) = [y 2 − 4y + 4 − 3(y − 2) + 9]
9
1
f (y) = [y 2 − 7y + 19]
9
161 CEDERJ](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-163-320.jpg)





![Fun¸oes composta e inversa
c˜
´
MODULO 1 - AULA 14
Exerc´
ıcios - S´rie A
e
1. Dados f (x) = x2 − 1, g(x) = 2x. Determine:
a) f ◦ g(x) b) f ◦ f (x) c) g ◦ f (x) d) g ◦ g(x).
2. (UFF 96 - 2a fase) Sendo f a fun¸˜o real definida por f (x) = x2 −6x+8,
¯ ca
para todos os valores x > 3. Determine o valor de f −1 (3).
3. (UNI-RIO 97 - 1a fase) A fun¸˜o inversa da fun¸˜o bijetora f : R −
¯ ca ca
2x − 3
{−4} → R − {2} definida por f (x) = ´:
e
x+4
x+4 x−4 4x + 3
a) f −1 (x) = b) f −1 (x) = c) f −1 (x) =
2x + 3 2x − 3 2−x
−1 4x + 3 −1 4x + 3
d) f (x) = e) f (x) =
x−2 x+2
4. (UFF 2001) Dada a fun¸˜o real de vari´vel real f , definida por
ca a
x+1
f (x) = , x = 1:
x−1
a) determine (f ◦ f )(x) b) escreva uma express˜o para f −1 (x).
a
5. (UFRS - 81) Se P (x) = x3 − 3x2 + 2x, ent˜o {x ∈ R | P (x) > 0} ´:
a e
a) (0,1) b) (1,2) c) (−∞, 2) ∪(2, ∞) d) (0, 1) ∪(2, ∞) e) (−∞, 0) ∪(1, 2).
6. Se f (x) = 3x , ent˜o f (x + 1) − f (x) ´:
a e
a) 3 b) f (x) c) 2f (x) d) 3f (x) e) 4f (x)
7. (FUVEST SP) Se f : R → R ´ da forma f (x) = ax + b e verifica
e
f [f (x)] = x + 1, para todo real, ent˜o a e b valem, respectivamente:
a
1 1
a) 1 e b) −1 e c) 1 e 2 d) 1 e −2 e) 1 e 1
2 2
8. (FATEC SP) Seja a fun¸˜o f tal que f : (R − {−2}) → R, onde
ca
x−2
f (x) = · O n´ mero real x que satisfaz f (f (x)) = −1 ´:
u e
x+2
a) −4 b) −2 c) 2 d) 4 e) n.d.a.
9. Determine o dom´ ınio de cada fun¸˜o:
ca
√ √
I) f (x) = |x| II) f (x) = x2 − 4 III) f (x) = 1/x IV) f (x) = x/x
167 CEDERJ](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-169-320.jpg)


![9. (CESGRANRIO-79) Seja f : (0; +∞) → (0; +∞) a fun¸˜o dada por
ca
1
f (x) = 2 e f −1 a fun¸˜o inversa de f . O valor de f −1 (4) ´:
ca e
x
a) 1/4 b) 1/2 c) 1 d) 2 e) 4
1
10. (UFMG-80) Seja f (x) = · Se x = 0, uma express˜o para f (1/x)
a
x2 +1
´:
e
x2 + 1 x2 1 1
a) x2 + 1 b) c) d) +x e)
x2 x2 + 1 x2 x2 + 1
11. Considere a fun¸˜o F (x) = |x2 − 1| definida em R. Se F ◦ F representa
ca
a fun¸˜o composta de F com F , ent˜o:
ca a
a) (F ◦ F )(x) = x|x2 − 1|, ∀ x ∈ R
b) ∃ y ∈ R | (F ◦ F )y = y
c) F ◦ F ´ injetora
e
d) (F ◦ F )(x) = 0 apenas para 2 valores reais de x
e) todas as anteriores s˜o falsas.
a
Gabarito
S´rie A
e
1. a) f ◦ g(x) = 4x2 − 1 b) f ◦ f (x) = x4 − 2x2
c) g ◦ f (x) = 2x2 − 2
x+1
d) g ◦ g(x) = 4x 2. 5 3. c) 4. a) (f ◦ f )(x) = x b) f −1 (x) =
x−1
5. d) 6. c) 7. a) 8. c) 9. I) R, II) {x ∈ R | x ≤ −2 e x ≥ 2},
III) R∗ , IV) R∗ 10. I) D(f ) = [−5, 1], Im(f ) = [0, 12] II) D(f ) = [0, 3],
+
Im(f ) = [−1, 2] 11. a)
S´rie B
e
1
1. f (x) = x2 − 1 2. a) (g ◦ f )(x) = x b) 13 3. d) 4. a) 5. b)
4
6. a) 7. e) 8. a) 9. b) 10. c) 11. e)
Auto-avalia¸˜o
ca
Antes de passar ` aula seguinte, vocˆ deve resolver todos os exerc´
a e ıcios
da S´rie A. A S´rie B fica como exerc´ de aprofundamento.
e e ıcio](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-172-320.jpg)


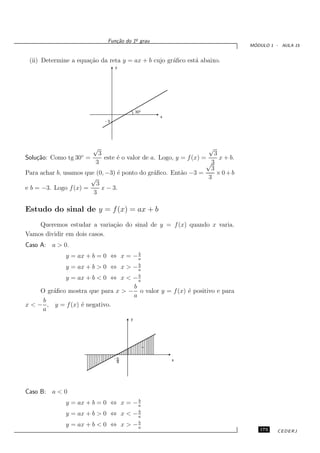


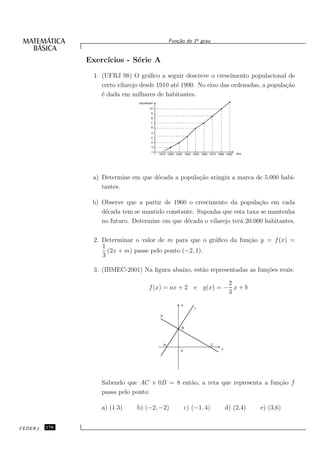




![o
Fun¸˜o do 1¯ grau
ca
´
MODULO 1 - AULA 15
1+x
7. (PUC-SP) O dom´
ınio da fun¸˜o real dada por f (x) =
ca ´:
e
x−4
a) {x ∈ R | x > −1 e x < 4}
b) {x ∈ R | x < −1 ou x > 4}
c) {x ∈ R | x ≥ −1 e x ≥ 4}
d) {x ∈ R | x ≤ −1 ou x > 4}
e) n.r.a.
8. (UNICAMP) Duas torneiras s˜o abertas juntas; a 1a enchendo um
a ¯
a
tanque em 5 horas, a 2¯ enchendo outro tanque de igual volume em
4 horas. No fim de quanto tempo, a partir do momento em que as
torneiras s˜o abertas, o volume que falta para encher o 2o tanque ´ 1/4
a ¯ e
do volume que falta para encher o 1o tanque?
¯
9. (ESPM/SP) Uma empresa de bicicletas possui um custo unit´rio de a
produ¸˜o de US$ 28,00 e pretende que este valor represente 80% do
ca
pre¸o de venda ao lojista. Esta, por sua vez, deseja que o valor pago ao
c
fabricante seja apenas 70% do total que custar´ ao consumidor final.
a
Quanto o consumidor final dever´ pagar por uma bicicleta?
a
2x − 3
10. (PUC/MG) Seja f : R → R uma fun¸˜o definida por f (x) =
ca ·
5
7
O valor de x na equa¸˜o f −1 (x) = ´:
ca e
2
a) 3/8 b) 4/5 c) 2/7 d) −4/5 e) −3/8
Gabarito
S´rie A
e
1. a) a d´cada de 40 b) 2040 < A < 2050 2. m = 7 3. b)
e
3 √
4. a) f (x) = y = x − 3 b) y = −2x + 6 c) y = 3x + 12 d)
5
y = −x − 10 5. a) S = {x ∈ R | x > −10} = (−10, ∞) b) {x ∈ R | x ≤
2} =) − ∞, 2] c) {x ∈ R | x < 5} = (−∞, 5) d) {x ∈ R | x > 1} = (1, ∞)
e) {x ∈ R | x < 0} = (−∞, 0) f) {x ∈ R | x ≤ 0} = (−∞, 0] 6. c) 7. e)
8. b) 9. e) 10. c) 11. e) 12. a) 13. c) 14. c) 15. b) 16. d)
181 CEDERJ](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-183-320.jpg)



![Fun¸˜o quadr´tica
ca a
´
MODULO 1 - AULA 16
Determina¸˜o das ra´
ca ızes
√
−b ± ∆
Para ax2 + bx + c = 0, x = .
2a
Ou seja √ √
−b + ∆ −b − ∆
x1 = e x2 = ,
2a 2a
s˜o as ra´
a ızes.
(I) Soma e produto das ra´
ızes
√ √
−b + ∆ −b − ∆
x1 + x2 = + =
2a 2a
−b b b
= − =−
2a √ 2a a √
−b + ∆ −b − ∆
x1 · x2 = · =
2a √ 2a √
(−b + ∆)(−b − ∆)
= =
4a2
b2 − ∆ b2 − (b2 − 4ac)
= = =
4a2 4a2
4ac c
= 2 =
4a a
b c
x1 + x2 = − , x1 · x2 =
a a
Nota: Se f (x) = y = ax2 + bx + c
b c
y = a x2 + x+ .
a a
Ent˜o chamando de S a soma das ra´ e de P o produto das ra´
a ızes ızes, encon-
tramos
y = a(x2 − Sx + P ).
(II) Fatora¸˜o da fun¸˜o quadr´tica
ca ca a
Afirmamos que
y = f (x) = ax2 + bx + c = a(x − x1 )(x − x2 ).
De fato,
a(x − x1 )(x − x2 ) =
a(x2 − x1 x − x2 x + x1 x2 ) =
a[x2 − (x1 + x2 )x + x1 x2 ] =
b c
a x2 + x+ = ax2 + bx + c
a a
185 CEDERJ](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-187-320.jpg)



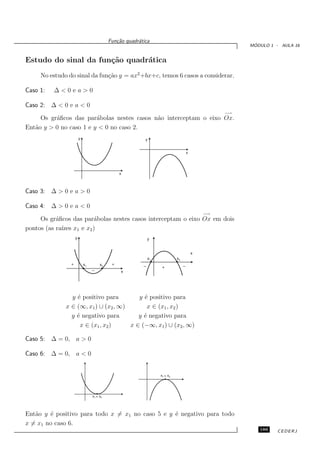

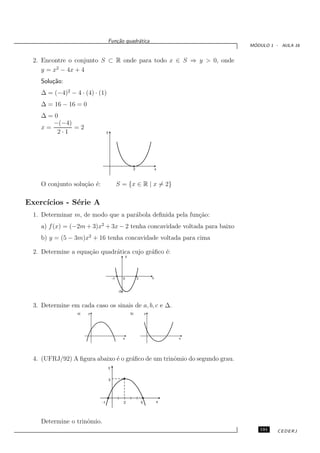







![Fun¸˜o Modular
ca
´
MODULO 1 - AULA 17
3. Resolva a inequa¸˜o |2x − 1| ≤ 4
ca
Solu¸˜o: (Veja a propriedade 5)
ca
|2x − 1| ≤ 4 ⇒ −4 ≤ 2x − 1 ≤ 4
3
−4 ≤ 2x − 1 ⇒ − 2 ≤ x
5
2x + 3 ≤ 4 ⇒ x ≤ 2
O conjunto solu¸˜o S da inequa¸˜o ´ o conjunto:
ca ca e
3 5
S= − , .
2 2
4. Resolva a inequa¸˜o |x2 − 4| ≥ 4
ca
Solu¸˜o: (Veja a propriedade 4)
ca
|x2 − 4| ≥ 4 ⇒ x2 − 4 ≥ 4 ou x2 − 4 ≤ −4
√ √ √
x2 − 4 ≥ 4 ⇒ x2 ≥ 8 ⇒ x ≥ 8 = 2 2 ou x ≤ −2 2
x2 − 4 ≤ −4 ⇒ x2 ≤ 0 ⇒ x = 0
Portanto o conjunto solu¸˜o S ´ composto de todos os valores x tais
ca e
√ √
que x = 0 ou x ≤ −2 2 ou x ≥ 2 2.
√ √
Ent˜o
a S = {0} ∪ (−∞, −2 2] ∪ [2 2, ∞).
Exerc´
ıcios - S´rie A
e
1. O gr´fico que melhor representa a fun¸˜o f (x) = |x + 1| − |x − 1| ´:
a ca e
a) b) y c) y
y
-1 1 2
x
2
-1 1 x
-2
-1 1 x -2
d) y e)
2 y
2
-1 1 x
-2 -1 1 2 x
-2
2. (Uni-Rio - 99) Sejam as fun¸˜es
co
f :R → R g:R → R
e
x → y = |x| x → x2 − 2x − 8
Fa¸a um esbo¸o do gr´fico da fun¸˜o f og.
c c a ca
199 CEDERJ](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-201-320.jpg)
![Fun¸˜o Modular
ca
3. (UFRJ - 99) Durante o ano de 1997 uma empresa teve seu lucro di´rio
a
L dado pela fun¸˜o
ca
L(x) = 50(|x − 100| + |x − 200|)
onde x = 1, 2, ..., 365 corresponde a cada dia do ano e L ´ dado em
e
reais. Determine em que dias (x) do ano o lucro foi de R$ 10.000, 00.
4. (FUVEST) Determine as ra´ das seguintes equa¸˜es:
ızes co
a) |2x − 3| = 5 b) |2x2 − 1| + x = 0
5. (Osec-SP) O conjunto solu¸˜o da inequa¸˜o |x + 1| > 3 ´ o conjunto
ca ca e
dos n´ meros reais x tais que:
u
a) 2 < x < 4 b) x < −4 ou x > 2 c) x ≤ −4 ou x > 2
d) x < −4 e x > 2 e) x > 2
6. (MACKENZIE-SP) A solu¸˜o da inequa¸˜o |x| ≤ −1 ´ dada pelo con-
ca ca e
junto:
a) ∅ b) ] − 1; 1[ c) [−1; ∞[ d) [−1; 1] e) ] − ∞; −1]
7. (PUC/CAMPINAS-SP) Na figura abaixo tem-se o gr´fico da fun¸˜o f,
a ca
de R em R, definida por:
a) f(x)=|x + 1|
b) f(x)=|x − 1|
c) f(x)=|x| − 1
1
d) f(x)=|x2 − 1|
e) f(x)=|1 − x| 1
8. (UECE) Sejam Z o conjunto dos n´ meros inteiros, S = {x ∈ Z;
u
2
x − 3x + 2 = 0} e T = {x ∈ Z; |x − 1| < 3}. O n´ mero de ele-
u
mentos do conjunto T − S ´:
e
a) 1 b) 2 c) 3 d) 4 e) 5
9. (Cesgranrio) A soma das solu¸˜es reais de |x + 2| = 2|x − 2| ´:
co e
1 2 19 20
a) b) c) 6 d) e)
3 3 3 3
10. (CESGRANRIO) Trace o gr´fico da fun¸˜o f de R em R, definida por
a ca
f (x) = (x2 − 1) + |x2 − 1| + 1.
CEDERJ 200](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-202-320.jpg)

![Fun¸˜o Modular
ca
4. (UFMG) Se f (x) = |x| + 1 e g(x) = −x2 + 6x − 10 para todo x real,
ent˜o pode-se afirmar que f (g(x)) ´ igual a:
a e
a) x2 + 6x − 11
b)x2 + 6x − 9
c) x2 − 6x + 11
d) x2 − 6x + 9
e) x2 − 6x − 11
5. (UFF - 99) Considere o sistema
y > |x|
y≤ 2
A regi˜o do plano que melhor representa a solu¸˜o ´:
a ca e
y y
a) b) y
c)
2
2 2
0 x
0 x 0 x
y y
d) e)
2 2
0 x 0 x
1
6. (FEI-SP) A solu¸˜o da inequa¸˜o
ca ca < 1 ´:
e
|1 − 2x|
a) 0 < x < 1
b) x < −1 ou x > 0
c) −1 < x < 0
d) x < 0 ou x > 1
e) x < −1 ou x > 1
7. (F.C. Chagas-BA) O maior valor assumido pela fun¸˜o y = 2−|x−2| ´:
ca e
a) 1 b) 2 c) 3 d) 4 e) ∞
8. (CESGRANRIO) Seja a fun¸˜o definida no intervalo aberto ] − 1, 1[
ca
x −1
por f (x) = . Ent˜o, f
a vale:
1 − |x| 2
1 1 −1
a) b) c) d) −1 e) −2
2 4 2
CEDERJ 202](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-204-320.jpg)

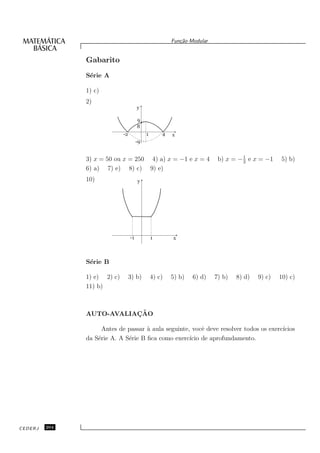

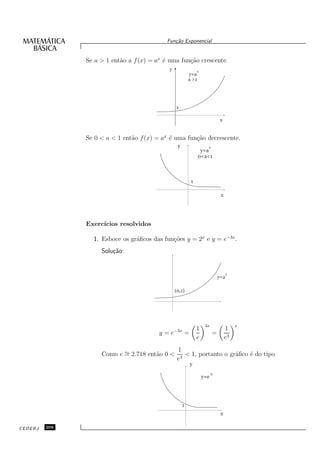



![Fun¸˜o Exponencial
ca
√
2 16 − 12 4±
A equa¸˜o 3y − 4y + 1 = 0 tem solu¸˜es y =
ca co ⇒ y=1
6
1 1
ou y = · Logo, 3y 2 − 4y + 1 ≤ 0 ⇒ ≤ y ≤ 1. Portanto, devemos
3 3
resolver as inequa¸˜es.
co
1
≤ 3x ≤ 1 .
3
1
≤ 3x ⇒ 3−1 ≤ 3x ⇒ −1 ≤ x
3
3x ≤ 1 ⇒ 3x ≤ 30 ⇒ x ≤ 0.
O conjunto solu¸˜o da inequa¸˜o ´ o intervalo fechado [−1, 0].
ca ca e
3. Determine o dom´
ınio da fun¸˜o
ca
√
f (x) = 3x − 1
Solu¸˜o: Como s´ tem sentido ra´
ca o ızes quadradas de n´ meros positivos
u
x
ou nulos, devemos ter 3 − 1 ≥ 0. Assim,
3x ≥ 1 ⇒ 3x ≥ 30 ⇒ x ≥ 0
Portanto, Dom(f ) = [0, ∞).
Exerc´
ıcios - S´rie A
e
1. (CESGRANRIO-RJ) O gr´fico que melhor representa a fun¸ao
a c˜
2x
f (x) = e ´:e
y
a) b) c)
y
y
1
1
1
x
x
x
y
d) y e)
1
x
x
CEDERJ 210](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-212-320.jpg)
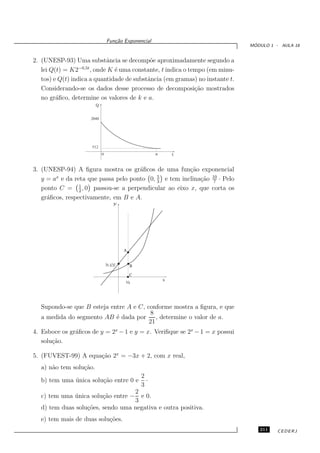
![Fun¸˜o Exponencial
ca
6. (UFF 95) Em uma cidade, a popula¸˜o de pessoas ´ dada por
ca e
P (t) = P o2t e a popula¸˜o de ratos ´ dada por R(t) = Ro4t , sendo
ca e
o tempo medido em anos. Se em 1992 havia 112.000 pessoas e 7.000
ratos, em que ano o n´ mero de ratos ser´ igual ao de pessoas?
u a
7. (UNI-RIO) O qu´druplo da solu¸˜o da equa¸˜o 54x+3 = 25 ´:
a ca ca e
1
a) 1 b) −1 c) −16 d) 5 e) −
4
16
8. (UNI-RIO) O valor de x na equa¸˜o: 3x−1 + 2 · 3x+1 − 3x =
ca ´:
e
27
a) 2 b) 2/3 c) 1/2 d) −1/2 e) −2
9. (PUC) A raiz da equa¸˜o 22x − 15 · 2x − 16 = 0 ´:
ca e
a) 16 b) 12 c) 10 d) 8 e) 4
2 −7x+5
10. (CESGRANRIO) O n´ mero de ra´ reais de 32x
u ızes = 1 ´:
e
a) 0 b) 1 c)2 d) 3 e) maior que 3
11. Determine o dom´ ınio das fun¸˜es reais:
co
√
a) f (x) = 2x2 −1 − 1
1
b) f (x) = x
4 − 2x
x−3
1 1
12. (UNI-RIO-96) Assinale o conjunto-solu¸˜o da inequa¸˜o
ca ca ≤ ·
2 4
a) ] − ∞, 5]
b) [4, +∞[
c) [5, +∞[
d) {x ∈ R | x ≤ −5}
e) {x ∈ R | x ≥ −5}
2 +5x−3
13. (UNI-RIO-99) Seja uma fun¸˜o f definida por f (x) = 2x
ca . Deter-
mine os valores de x tais que f (x) seja menor do que 8.
14. (PUC-SP) O valor de x, x ∈ R, que ´ solu¸˜o da equa¸˜o 4x+2 = 8−x+3 ,
e ca ca
´:
e
1 1 4
a) 0 b) c) d) 1 e)
5 2 3
CEDERJ 212](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-214-320.jpg)
![Fun¸˜o Exponencial
ca
´
MODULO 1 - AULA 18
Exerc´
ıcios - S´rie B
e
1. Esboce o gr´fico de cada fun¸˜o abaixo e determine o conjunto imagem
a ca
a) y = 3x − 1 b) y = |2x − 2|
√
2. (FESP SP) Se x 2 = 16x , ent˜o os valores de x s˜o:
a a
1 1 1 1 1 1 1
a) 0 e b) e − c) e − d) e − e) 0 e 1
2 4 2 2 2 8 8
3. (UNI-RIO - 2000) O conjunto-solu¸˜o da inequa¸˜o x2x ≥ xx+3 , onde
ca ca
x > 0 e x = 1, ´:
e
a) ]0, 1[∪[3, +∞[ b) {x ∈ R | 0 < x < 1} c) [3, +∞[ d) R e) ∅
x(x+1) x+1
1 1
4. (FESP-SP) A solu¸˜o da inequa¸˜o
ca ca ≥ ´:
e
3 3
1
a) x ≤ 0 b) x ≥ 0 c) x ≤ −1 ou x ≥ 1 d) −1 ≤ x ≤ 1 e) x ≥
3
5. (PUC-RS) A solu¸˜o da equa¸˜o 2x+1 − 23−x − 6 = 0 pertence ao
ca ca
intervalo:
a) −1 ≤ x < 2 d) 2 < x ≤ 4
b) −1 < x ≤ 2 e) 3 ≤ x < 4
c) 2 < x < 4
6. (MACKENZIE-SP) O valor de m, m ∈ R, que satisfaz a equa¸˜o
ca
10
(2m+2 )3 = 2 3 ´:
e
8 4 8
a) − b) 6 c) − d) − e) −6
9 3 9
7. (FEI-SP) Para que valor real de x temos 8x − 8−x = 3 · (1 + 8−x ):
1 2
a) 4 b) c) 2 d)1 e)
2 3
8. (PUC-MG) Se 3x+1 + 3x−1 − 3x−2 = 87, ent˜o 2x − 1 ´ igual a:
a e
a) 5 b) 6 c) 7 d) 8 e) 9
9. (UECE) Se 64|x| − 2 · 8|x| + 1 = 0, ent˜o x2 ´ igual a:
a e
1 1
a) 0 b) c) d) 1 e) 4
9 4
2x + 3y = 11
10. (CESGRANRIO) Se (x, y) ´ solu¸˜o do sistema
e ca a
2x − 3y = 5
soma (x + y) ´ igual a:
e
a) 11 b) 3 d) 6 d) 4 e) 5
213 CEDERJ](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-215-320.jpg)
![Fun¸˜o Exponencial
ca
Gabarito
S´rie A
e
1) c) 2) K = 2048 a = 4 min 3) a = 4
4)
y
1
1 x
possui duas solu¸˜es: x = 0 e x = 1
co
5) b) 6) Em 1996 7) b) 8) e) 9) e) 10) c) 11) a) D(f ) =
(−∞, −1] ∪ [1, ∞) b) D(f ) = R − {0} 12) c) 13) (−6, 1) 14) d)
S´rie B
e
1)
a) y
x
b) y
2
1
x
2) c) 3) a) 4) d) 5) b) 6) a) 7) e) 8) a) 9) a) 10) d)
Auto-avalia¸˜o
ca
Antes de passar ` aula seguinte, vocˆ deve resolver todos os exerc´
a e ıcios
da S´rie A. A S´rie B fica como exerc´ de aprofundamento.
e e ıcio
CEDERJ 214](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-216-320.jpg)
















![Trigonometria
´
MODULO 1 - AULA 20
Aula 20 – Trigonometria
Introdu¸˜o
ca
O termo trigonometria significa, em uma tradu¸˜o literal, medidas de
ca
um triˆngulo. Mais especificamente, a trigonometria estuda rela¸˜es envol-
a co
vendo ˆngulos e raz˜es dos lados de triˆngulos semelhantes.
a o a
Historicamente as primeiras rela¸˜es trigonom´tricas j´ eram conheci-
co e a
das pelos eg´
ıpcios e babilˆnicos em 1600 A.C., aproximadamente. Na antigui-
o
dade, muitos avan¸os na trigonometria se devem principalmente as aplica¸˜es
c co
em astronomia (ver [1], [2], [3] e [4]):
• Aristarco (310-230 A.C.), desenvolveu um consistente m´todo para es-
e
timar o raio da lua e do sol bem como de suas distˆncias relativas a
a
terra.
• Erat´stenes (276-194 A.C.), por sua vez, calculou uma das mais famosas
o
estimativas para o per´
ımetro da circunferˆncia da terra e seu raio. Para
e
isso, comparou posi¸˜es relativas de sombras exatamente ao meio dia do
co
solst´ de ver˜o em duas cidades: Siene e Alexandria. Assim, obteve
ıcio a
que o ˆngulo α da figura abaixo era cerca de 1/50 do circulo.
a
a
dri
an
ex
Al α
R
α Siene
O
Sabendo que a distˆncia entre as duas cidades era cerca de 925 Km,
a
estimou que o per´
ımetro da terra seria de cerca de 925 x 50 = 46.250
km, sendo que o valor correto ´ de 40.075 km.
e
• O astrˆnomo grego Hiparco (180-125 A.C.) ´ considerado o pai da tri-
o e
gonometria devido as suas importantes contribui¸˜es. A ele ´ atribu´
co e ıdo
a constru¸˜o da primeira tabela trigonom´trica e tamb´m uma das pri-
ca e e
meiras referˆncias a utilizar a medida do ˆngulo em graus (sistema
e a
sexagesimal).
231 CEDERJ](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-233-320.jpg)


















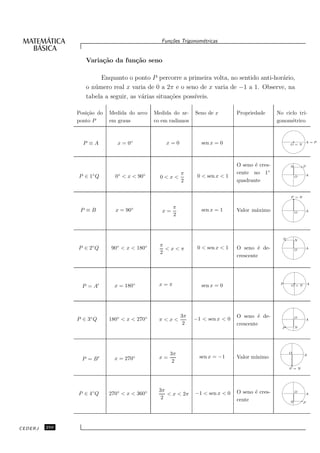
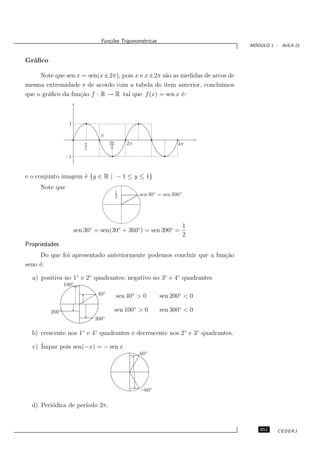


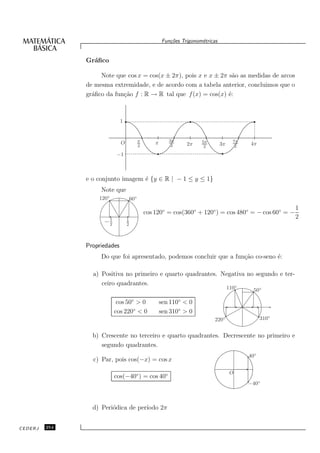

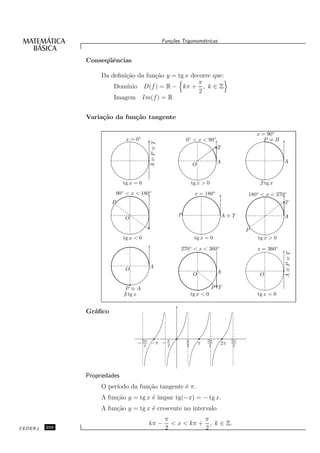

![Fun¸oes Trigonom´tricas
c˜ e
3 3π
3. Se tg x = eπ<x< , determine o valor de cos x − sen x.
4 2
Solu¸˜o
ca
Seja o triˆngulo retˆngulo temos:
a a
5
3
x
4
3 3 4
tg x = , sen x = e cos x =
4 5 5
3π 3 3 4
Tomando π < x < , teremos: tg x = , sen x = − e cos x = − .
2 4 5 5
4 3 1
Portanto cos x − sen x = − − − =− .
5 5 5
Exerc´
ıcios propostos
1. Determine o conjunto verdade da equa¸˜o | tg x| − 1 = 0 no intervalo
ca
0 ≤ x ≤ 2π.
2. Determine o conjunto verdade da equa¸˜o sen x+cos x = 0, no intervalo
ca
[4, 3π].
π
3. Se 0 < α < e sen α = a. Determine tg(π − α).
2
4. Na esta¸˜o de trabalho de pintura de pe¸as de uma f´brica, a press˜o
ca c a a
em um tambor de ar comprimido varia com o tempo conforme a ex-
π
press˜o P (t) = 50 + 50 sen t −
a , t > 0. Determine o instante t que
2
corresponde ao valor m´ ınimo da press˜o.
a
Gabarito
π 3π 5π 7π
1. V = , , ,
4 4 4 4
7π 11π
2. V = ,
4 4
−a
3. √
1 − a2
4. 2π
CEDERJ 258](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-260-320.jpg)

![Fun¸oes Trigonom´tricas
c˜ e
Fun¸˜o co-secante
ca
1
Sabemos que csc x = .
sen x
Podemos concluir que a fun¸˜o f (x) = y = csc x, tem:
ca
• D(f ) = R − {kπ, k ∈ Z} pois a fun¸˜o co-secante n˜o existe quando a
ca a
fun¸˜o seno ´ zero
ca e
(sen x = 0 ⇔ x = kπ, k ∈ Z)
• Im(f ) = {y ∈ R | y ≤ −1 ou y ≥ 1}, pois a fun¸˜o seno tem imagem
ca
com valores −1 ≤ y ≤ 1.
• O per´
ıodo da fun¸˜o co-secante ´ 2π.
ca e
• A fun¸˜o y = csc x ´ ´
ca e ımpar, csc(−x) = − csc x.
• Sinais
A co-tangente de um arco ´ positiva no 1◦ e 2◦ quadrantes e negativa
e
◦ ◦
no 3 e 4 quadrantes.
Exerc´
ıcios resolvidos
1. Resolver a equa¸˜o sec x = 2, x ∈ [0, 2π].
ca
Solu¸˜o
ca
sec x = 2 1 1
1 ⇒ = 2 ⇒ cos x =
sec x = cos x 2
cos x
π
3
5π
3
π 5π
Para 0 ≤ x ≤ 2π, temos V = , .
3 3
π
2. Se x = , calcular o valor da express˜o
a
6
E = sec x + cotg x + csc(3x)
Solu¸˜o
ca
π 2π π π π π
E = sec + cotg + csc 3 · = sec + cotg + csc
6 6 6 6 3 2
1 1 1 √
= + π + = 3+1
cos π
6
tg 3 sen π
2
CEDERJ 260](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-262-320.jpg)
















![Transforma¸oes
c˜
´
MODULO 1 - AULA 23
Aula 23 – Transforma¸˜es
co
Fun¸˜es Trigonom´tricas de arcos: soma; diferen¸a; du-
co e c
plo; triplo; metade. Transforma¸˜o em produto
ca
F´rmula da Adi¸˜o
o ca
Cosseno da Soma
Sejam C, D e E os pontos do ciclo associados aos n´ meros a, a + b e
u
−b, respectivamente. Em rela¸˜o ao eixo cartesiano XOY as coordenadas
ca
desses pontos s˜o:
a
y
B a+b
D C
a
C = (cos a, sen a)
A′ A D = (cos(a + b), sen(a + b))
0 x
E = (cos b, − sen b)
−b A = (1, 0)
B E ′
⌢ ⌢
Os arcos AD e EC tˆm a mesma medida, portanto, as cordas AD e
e
CE s˜o iguais, ent˜o:
a a
d2 2 2 2
AD = (xD − xA ) + (yD − yA ) = [cos(a + b) − 1] + [sen(a + b) − 0]
2
= 2 − 2 cos(a + b)
dEC = (xC − xE )2 + (yC − yE )2 = [cos a − cos b]2 + [sen a + sen b]2
2
= 2 − 2 cos a · cos b + 2 · sen a · sen b
Como dAD = dEC ⇒ 2 − 2 cos a cos b + 2 sen a sen b = 2 − 2 cos(a + b).
Da´ cos(a + b) = cos a cos b − sen a sen b .
ı
Cosseno da Diferen¸a
c
cos(a − b) = cos(a + (−b)) = cos a · cos(−b) − sen a · sen(−b)
= cos a cos b + sen a sen b
ent˜o cos(a − b) = cos a cos b + sen a sen b
a
277 CEDERJ](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-279-320.jpg)


















![Equa¸oes Trigonom´tricas
c˜ e
2. Resolver a equa¸˜o sec2 x = 1 + tg x.
ca
Solu¸˜o
ca
sec2 x = 1 + tg x ⇒ 1 + tg2 x = 1 + tg x ⇒ tg2 x − tg x = 0
⇒ tg x(tg x − 1) = 0 ⇒ tg x = 0 ou tg x = 1
π
S = x ∈ R | x = kπ ou x = kπ + , k∈Z
4
Solu¸˜es de uma equa¸˜o dentro de um certo intervalo
co ca
Quando tivermos resolvendo uma equa¸˜o pertencente a um determi-
ca
nado intervalo I devemos fazer o seguinte procedimento:
1◦ ) Resolvemos normalmente a equa¸˜o, n˜o tomando conhecimento do
ca a
intervalo I at´ obtermos a solu¸˜o geral.
e ca
2◦ ) Obtida a solu¸˜o geral, atribu´
ca ımos a k ∈ Z todos os valores inteiros
que acarretem as solu¸˜es estarem em I.
co
Exerc´
ıcios Resolvidos
1
1. Determinar x ∈ [0, 2π] tal que sen 4x =
2
Solu¸˜o
ca
1
sen 4x = , x ∈ [0, 2π]
2
π x = π + 2kπ
4x = + 2kπ
π 6 24 4
sen 4x = sen ⇒ ou ⇒ ou
6
4x = π − π + 2kπ
x = 5π + 2kπ
6 24 4
Vamos calcular as solu¸˜es que pertencem ao intervalo [0, 2π]
co
π 5π 37π 41π
k = 0 ⇒ x1 = , x2 = k = 3 ⇒ x7 = , x8 =
24 24 24 24
13π 17π 49π 53π
k = 1 ⇒ x3 = , x4 = k = 4 vamos achar e
24 24 24 24
25π 29π
k = 2 ⇒ x5 = , x6 = Estas solu¸˜es n˜o pertencem ao
co a
24 24
intervalo fechado de 0 a π.
π 5π 13π 17π 25π 29π 37π 41π
S= , , , , , , ,
24 24 24 24 24 24 24 24
CEDERJ 296](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-298-320.jpg)
![Equa¸oes Trigonom´tricas
c˜ e
´
MODULO 1 - AULA 24
2. Achar as solu¸˜es de tg 6x = tg 2x para 0 ≤ x ≤ 2π.
co
Solu¸˜o
ca
tg 6x = tg 2x, x ∈ [0, 2π]
kπ
⇒ 6x = 2x + kπ ⇒ 4x = kπ ⇒ x =
4
3π 3π
k=0⇒x=0 k=3⇒x= k=6⇒x=
4 2
π 7π
k=1⇒x= k=4⇒x=π k=7⇒x=
4 4
π 5π
k=2⇒x= k=5⇒x= k = 8 ⇒ x = 2π
2 4
π 3π 5π 7π
Excluindo os valores , , , para os quais n˜o existem as
a
4 4 4 4
tangentes de 6x e 2x, vem:
π 3π
S= 0, , π, , 2π
2 2
3. Encontre a soma das ra´ da equa¸˜o cos 2x = 0 no intervalo [0, π].
ızes ca
Solu¸˜o
ca
cos 2x = 0
Temos que cos 2x = cos2 x − sen2 x.
Da´ cos2 x − sen2 x = 0 ⇒ cos 2x = 0
ı
π π
Portanto, 2x = 2kπ ± ⇒ x = kπ ± (Solu¸˜o Geral).
ca
2 4
No intervalo [0, π] temos as solu¸˜es:
co
π π
k = 0 ⇒ x = 0π + =
4 4
π 3π
k=1⇒x=π− =
4 4
π 3π
Assim, a soma das ra´ ´ +
ızes e =π
4 4
Equa¸˜es Cl´ssicas
co a
Sugest˜es para resolver a equa¸˜o: a sen x + b cos x = c (a, b, c ∈ R∗ )
o ca
M´todo 1
e
Fazer mudan¸a de vari´vel
c a
au + bv = c
sen x = u e cos x = v e resolvemos o sistema
u2 + v 2 = 1
Calculando u e v, determinamos os poss´
ıveis valores de x.
297 CEDERJ](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-299-320.jpg)






![Fun¸oes Circulares Inversas
c˜
´
MODULO 1 - AULA 25
Aula 25 – Fun¸˜es Circulares Inversas
co
Fun¸˜o Arco-Seno
ca
A fun¸˜o seno, isto ´, f : R → R tal que f (x) = sen x n˜o ´ sobrejetora,
ca e a e
pois n˜o existe x ∈ R tal que sen x = 2, ou seja f (x) = 2.
a
π 3π π 3π
A fun¸˜o seno n˜o ´ injetora, pois =
ca a e e sen = sen , ou seja,
4 4 4 4
π 3π π 3π
f =f e = .
4 4 4 4
Para acharmos a fun¸˜o inversa da fun¸˜o seno, esta deve ser bijetora.
ca ca
π π
Consideremos ent˜o a fun¸˜o seno restrita ao intervalo − ,
a ca e com
2 2
π π
contradom´ [−1, 1], ou seja, g : − ,
ınio → [−1, 1] tal que g(x) = sen x.
2 2
sen x
1
−π
−π
2
π
2
π x
−1
Note que :
π π
(1) g ´ sobrejetora, j´ que ∀y, y ∈ [−1, 1], existe x ∈ − ,
e a tal que
2 2
sen x = y
π π
(2) g ´ injetora, j´ que no intervalo − ,
e a se x1 = x2 ⇒ sen x1 = sen x2 .
2 2
Logo de (1) e (2) g ´ bijetora, da´ g admite inversa que vamos denotar
e ı
−1
por g e vamos denominar de arco-seno.
π π
g −1 tem dom´ ınio [−1, 1], contradom´ ınio − , e associa a cada
2 2
π π
x ∈ [−1, 1], ∃y ∈ − , tal que y = arcsen x.
2 2
π π
Portanto y = arcsen x ⇔ sen y = x e − ≤ y ≤
2 2
Gr´fico da fun¸˜o arco-seno
a ca
Temos que os gr´ficos de duas fun¸˜es inversas entre si s˜o sim´tricas
a co a e
◦ ◦
em rela¸˜o ` reta que cont´m as bissetrizes do 1 e 3 quadrantes.
ca a e
305 CEDERJ](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-307-320.jpg)

![Fun¸oes Circulares Inversas
c˜
´
MODULO 1 - AULA 25
Fun¸˜o arco-cosseno
ca
A fun¸˜o cosseno, isto ´, f : R → R tal que f (x) = cos x n˜o ´
ca e a e
sobrejetora, pois n˜o existe x ∈ R tal que cos x = 4, ou seja, f (x) = 4.
a
π 5π π 5π
A fun¸˜o cosseno n˜o ´ injetora, pois
ca a e = e cos = cos , ou
3 3 3 3
π 5π π 5π
seja, f =f e = .
3 3 3 3
Para acharmos a fun¸˜o inversa da fun¸˜o cosseno, esta deve ser bije-
ca ca
tora.
Consideremos ent˜o a fun¸˜o cosseno restrita ao intervalo [0, π] e com
a ca
ınio [−1, 1], ou seja, g : [0, π] → [−1, 1] tal que g(x) = cos x.
contradom´
cos x
1
O π x
−1
Note que:
(1) g ´ sobrejetora, j´ que ∀y, y ∈ [−1, 1], existe x ∈ [0, π] tal que cos x = y.
e a
(2) g ´ injetora, j´ que no intervalo [0, π] se x1 = x2 ⇒ cos x1 = cos x2 .
e a
Logo de (1) e (2) temos que g ´ bijetora, da´ g admite inversa que vamos
e ı
denotar por g −1 e vamos denominar de arco-cosseno.
g −1 tem dom´ ınio [−1, 1], contradom´ ınio [0, π] e associa a cada
x ∈ [−1, 1], ∃y ∈ [0, π] tal que y = arccos x.
Portanto y = arccos x ⇔ cos y = x e 0 ≤ y ≤ π
Gr´fico da fun¸˜o arco-cosseno
a ca
Temos que os gr´ficos de duas fun¸˜es inversas entre si s˜o sim´tricas
a co a e
em rela¸˜o ` reta que cont´m as bissetrizes do 1◦ e 3◦ quadrantes.
ca a e
Gr´fico de g(x) = cos x
a Gr´fico de g −1(x) = arccos x
a
cos x arccos x
1 π
O π x
−1
−1 1 x
307 CEDERJ](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-309-320.jpg)



![Fun¸oes Circulares Inversas
c˜
´
MODULO 1 - AULA 25
12
6. Calcular cos 3 · arcsen
13
1 7
7. Calcular cos · arccos
2 25
1
8. Calcular tg 2 · arctg
5
√ √ π
9. Detemine o n´ mero de solu¸˜es da equa¸˜o arcsen x + arccos x =
u co ca
2
10. Calcular y = tg[arcsen(−0, 6)]
Gabarito
π
1. −
6
2. y = 1
√
3
3. x =
2
√
2 3
4. x =
3
π
5. −
10
2035
6. −
2197
4
7.
5
5
8.
12
9. infinitas solu¸˜es
co
3
10. −
4
311 CEDERJ](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-313-320.jpg)



![Inequa¸oes Trigonom´tricas
c˜ e
´
MODULO 1 - AULA 26
3. Determinar os valores de x ∈ [0, 2π] tal que sen 3x > 0
Solu¸˜o
ca
Fazendo 3x = y, temos sen y > 0
⇒ 2kπ < y < 2kπ + π, k ∈ Z
y
Como x = , resulta: A
3
2kπ 2kπ π
<x< +
3 3 3
Mas x ∈ [0, 2π] ent˜o temos que k = 0 ou k = 1 ou k = 2
a
π
k=0⇒0<x<
3
ou
2π
k=1⇒ <x<π
3
ou
4π 5π
k=2⇒ <x<
3 3
π 2π 4π 5π
S= x∈R|0<x< ou < x < π ou <x<
3 3 3 3
Inequa¸˜o do tipo cos x > m, m ∈ R
ca
Este tipo de inequa¸˜o se resolve da seguinte maneira: marcamos sobre
ca
o eixo dos cossenos o ponto P2 tal que OP2 = m. Tra¸amos por P2 a reta r
c
perpendicular ao eixo dos cossenos. As imagens dos reais x tais que cos x > m
est˜o na interse¸˜o do ciclo com o semi-plano situado ` direita de r.
a ca a
x A
O P2
Para finalizar, descreveremos os intervalos que conv´m ao problema.
e
315 CEDERJ](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-317-320.jpg)

![Inequa¸oes Trigonom´tricas
c˜ e
´
MODULO 1 - AULA 26
3. Resolver cos 2x + cos x ≤ 0
Solu¸˜o
ca
cos 2x + cos x ≤ 0 ⇒ cos2 x − sen2 x + cos x ≤ 0 ⇔
⇔ 2cos2 x − 1 + cos x ≤ 0 ⇔ 2cos2 x + cos x − 1 ≤ 0
√ −1+3
−1 ± 1+8 2
= −1
cos x = π
4 −1−3
= 1 3
2 2
1
2
π 5π −1
S= x∈R| ≤x≤ O
3 3
5π
3
1
4. Determinar x ∈ [0, 2π] tal que cos 4x ≤
2
Solu¸˜o
ca
1
Considere 4x = y ⇒ cos y ≤
2
Temos que: π
3
π 5π
+ 2kπ ≤ y ≤ + 2kπ, k ∈ Z
3 3
y O
Como x = , resulta:
4
5π
π kπ 5π kπ 3
+ ≤x≤ + , k∈Z
12 2 12 2
Mas x ∈ [0, 2π] ent˜o s´ interessam as solu¸˜es em que k = 0 ou k = 1
a o co
ou k = 2 ou k = 3
k = 0 ⇒ π ≤ x ≤ 5π
12 12
ou
k = 1 ⇒ 7π ≤ x ≤ 11π
12 12
ou
k = 2 ⇒ 13π ≤ x ≤ 17π
12 12
ou
k = 3 ⇒ 19π ≤ x ≤ 23π
12 12
317 CEDERJ](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-319-320.jpg)
![Inequa¸oes Trigonom´tricas
c˜ e
√
5. Resolver a inequa¸˜o: 2cos x ≤
ca 2 se x ∈ [0, π] π
3
Solu¸˜o
ca
1 1
2cos x ≤ 2 2 , como 2 > 1 ⇒ cos x ≤ O
2
π 5π
Da´
ı + 2kπ ≤ x ≤ 2kπ + , k ∈ Z 5π
3 3 3
π 5π
Como x ∈ [0, π], temos que k = 0 e ser´ ≤ x ≤ π. Note que
a > π.
3 3
π
S= x∈R| ≤x≤π
3
2cos2 x + cos x − 1
6. Resolver a inequa¸˜o
ca > 0 se x ∈ [0, π]
cos x − 1
Solu¸˜o
ca
2cos2 x + cos x − 1
Considere a inequa¸˜o dada
ca > 0 se x ∈ [0, π].
cos x − 1
Seja cos x = a.
2a2 + a − 1
Temos: >0
a−1
√ −1+3 1
2 −1 ± 1+8 4
=2
Resolvendo vem: 2a + a − 1 = 0 ⇒ a = −1−3
4 4
= −1
a−1=0⇒a=1
1 1
Temos ent˜o −1 < a < + ou a > 1, ou seja, −1 < cos x <
a ou
2 2
cos x > 1
Mas n˜o existe x ∈ R | cos x > 1
a /
1
Vamos ent˜o resolver a inequa¸˜o: −1 < cos x <
a ca
2
π
3
1
2
5π
3
Mas x ∈ [0, π] ent˜o a solu¸˜o no gr´fico ´:
a ca a e
1
2
Temos ent˜o que a solu¸˜o ´:
a ca e
π
S= x∈R| <x<π
3
CEDERJ 318](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-320-320.jpg)

![Inequa¸oes Trigonom´tricas
c˜ e
2. Resolver a inequa¸˜o tg x < 1
ca
Solu¸˜o
ca
Temos que
y r
π
4 T
A
5π
4
π π 5π
S = x ∈ R | 2kπ + 0 ≤ x < 2kπ + ou 2kπ + < x < 2kπ + ou
4 2 4
3π
2kπ + < x < 2kπ + 2π, k ∈ Z
2
√
3. Resolver a inequa¸˜o | tg x| ≤ 3
ca
Solu¸˜o
ca
√ √ √
| tg x| ≤ 3 ⇒ − 3 ≤ tg x ≤ 3 r
Temos ent˜o que:
a y π
T1
2π
3
3 √
3
A x
√
4π
− 3
5π
3 3
T2
π 2π 4π
x ∈ R | 2kπ + 0 ≤ x ≤ 2kπ + ou 2kπ + ≤ x ≤ 2kπ + ou
3 3 3
5π
2kπ + ≤ x < 2kπ + 2π, k ∈ Z
3
√
4. Determinar x ∈ [0, 2π] tal que 1 ≤ tg 3x < 3
Solu¸˜o
ca
√ T2
}
Considere 3x = y ⇒ 1 ≤ tg y < 3
π √
Temos que: 3 π
T1 3
4
}
A
1
π π y 5π
kπ + ≤ y < kπ + , como x = , vem 4 4π
4 3 3
3
kπ π kπ π
+ ≤x< + , k∈Z
3 12 3 9
CEDERJ 320](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-322-320.jpg)
![Inequa¸oes Trigonom´tricas
c˜ e
´
MODULO 1 - AULA 26
Mas x ∈ [0, 2π], ent˜o s´ interessam as solu¸˜es em que: k = 0 ou
a o co
k = 1 ou k = 2 ou k = 3 ou k = 4 ou k = 5.
π π
k=0⇒ ≤x<
12 9
5π 4π
k=1⇒ ≤x<
12 9
9π 7π
k=2⇒ ≤x<
12 9
13π 10π
k=3⇒ ≤x<
12 9
17π 13π
k=4⇒ ≤x<
12 9
21π 16π
k=5⇒ ≤x<
12 9
5. Determinar x ∈ [0, π] tal que tg x ≥ −1
Solu¸˜o
ca
Considere a inequa¸˜o: tg x > −1, x ∈ [0, π]
ca
3π
4
A
3π
5π
4
}
1
−1
2
π 3π
Note que x ∈ [0, π] ⇒ x∈R|0≤x< ou ≤x≤π
2 4
Exerc´
ıcios Propostos
1. Resolver as inequa¸˜es abaixo:
co
a) senx ≥ 0
√
2
b) | sen x| >
2
√
3 1
c) − ≤ cos x ≤
2 2
5
d) | cos x| >
3
√
3
2. Resolver a inequa¸˜o sen 3x ≤
ca se x ∈ [0, 2π].
2
3. Para que valores de x ∈ R existe log2 (2 sen x − 1)?
321 CEDERJ](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-323-320.jpg)
![Inequa¸oes Trigonom´tricas
c˜ e
4. Resolver a inequa¸˜o em R, sen x + cos x < 1.
ca
cos x
5. Determinar x ∈ [0, 2π] tal que ≤ 1.
cos 2x
4sen2 x − 1
6. Determinar no conjunto dos n´ meros reais o dom´ de y =
u ınio ,
cos x
0 ≤ x ≤ 2π.
√
√ 3
7. Resolver a inequa¸˜o em R, − 3 < tg x ≤
ca .
3
8. Resolver a inequa¸˜o tg2 2x ≤ tg 2x, x ∈ [0, 2π].
ca
9. Resolver a inequa¸˜o sen x > cos x, x ∈ [0, 2π].
ca
√ √
10. Resolver a inequa¸˜o em R, tg2 x − ( 3 − 1) tg x − 3 < 0.
ca
11. Resolver a inequa¸˜o sen2 x < 2 sen x, x ∈ [0, 2π].
ca
1
12. Resolver a inequa¸˜o em R,
ca < 2 tg x.
cos2 x
13. Resolver a inequa¸˜o | cos x| ≥ sen x, x ∈ [0, 2π].
ca
1 1
14. Para que valores de x ∈ R, sen x > e cos x ≥ .
2 2
15. Resolver a inequa¸˜o | sen x| > | cos x|, x ∈ [0, π].
ca
16. Resolver a inequa¸˜o (sen x + cos x)2 > 1, x ∈ [0, 2π]
ca
1
17. Resolver a inequa¸˜o sen 2x · sec2 x −
ca ≤ 0, x ∈ [0, 2π].
3
3
18. Se 0 ≤ α ≤ π , para todo x real, x2 + x + tg α > ent˜o
a
4
π
a) 0 < α <
4
π π
b) < α <
4 2
π 3π
c) < α <
2 4
3π
d) α =
4
e) n˜o existe α nestas condi¸˜es
a co
CEDERJ 322](https://image.slidesharecdn.com/apostilamatematicabasicavolunico-111208094313-phpapp01/85/Apostila-matematica-basica-vol-unico-324-320.jpg)