Alguns tópicos de geometria

ALGUNS TÓPICOS DE GEOMETRIA
Ângulos
1- ÂNGULOS SUPLEMENTARES  Dois ângulos são suplementares quando a sua soma for igual a
180º.
RST e UST são suplementares, pois 120º + 60º = 180º.
Observem na ilustração ao lado os ângulos formados pela Avenida das Flores e a Rua das Margaridas.
Agora responda:
1- Eles são suplementares? Por que?
2- Você sabe dizer qual deve ser a medida do ângulo
assinalado em vermelho formado pela Avenida das Flores e a Rua dos Lírios?
Através do uso das equações descubra o valor de x na figura abaixo:
1

2- ÂNGULOS COMPLEMENTARES  dois ângulos são complementares quando a sua soma for igual
a 90º .
AÔC e CÔB são ângulos complementares.
Se AÔC mede 30º , CÔB mede 60º, pois 30º + 60º = 90º.
Da mesma forma, na figura abaixo, RST e TSU são complementares, pois a soma de suas medidas é 90º.
Se RST mede 25º, então TSU mede 65º, que é o que falta para completar 90º.
 90º - 25º = 65º
Exercícios
1- Usando apenas cálculo mental, responda:
a) Um ângulo de 35º e um de 65º são complementares?______________
b) Um ângulo de 58º e um de 32º são complementares?______________
c) Um ângulo de 70º e um de 110º são complementares?_____________
d) Um ângulo de 86º e um de 104º suplementares?___________
2- Observe a figura e responda:
a) Qual é o valor de x?
b) Qual a medida do ângulo AÔB?
c) Qual é a medida do ângulo BÔC?
2

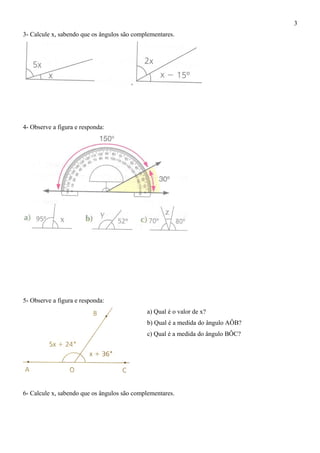
3- Calcule x, sabendo que os ângulos são complementares.
a) Qual é o valor de x?
b) Qual é a medida do ângulo AÔB?
c) Qual é a medida do ângulo BÔC?
6- Calcule x, sabendo que os ângulos são complementares.
3

7- Considere a figura abaixo, em que a, b, c, x, y e z são medidas dos ângulos assinalados.
a) Qual o valor, em graus, de a + b + c?________________
b) Qual o valor, em graus, de x + y + z?________________
c) Qual o valor, em graus, de a + b + c + x + y + z?________
8- Determine o valor de x:
3- BISSETRIZ DE UM ÂNGULO
Na figura ao lado o ângulo AÔB mede 60º.
A semi-reta OM dividiu esse ângulo em dois ângulos congruentes AÔM e BÔM.
• med (AÔM) = 30º
• méd (BÔM) = 30º
A Semi-reta OM é a bissetriz de AÔB.
Portanto a bissetriz de um ângulo:
• é uma semi-reta de origem do vértice;
• divide esse ângulo em dois ângulos congruentes.
4

1- Na figura, OM é a bissetriz de AÔB, que é um ângulo reto. Responda:
a) Qual é a medida de AÔM?
b) Qual é, em graus, o valor de x?
2- Calcule x, em cada caso, sabendo-se que OC é bissetriz do ângulo dado.
4- ÂNGULOS NOS TRIÂNGULOS
Já sabemos que a soma dos ângulos internos de qualquer triângulo é sempre 180º.
Vamos utilizar os princípios da resolução de problemas através da equação e calcular os ângulos internos
dos triângulos.
Vejamos:
Descubra quanto vale cada ângulo interno desse triângulo.
1- Calcule as medidas de x, y e z.
5

2- Calcule os ângulos desconhecidos.
5- ANGULOS NOS QUADRILÁTEROS
Em cada quadrilátero, ao dividi-lo no meio, podemos formar dois triângulos. Sabemos que a soma dos
ângulos internos de todo triângulo é sempre 180º. Por conseqüência, tendo dois triângulos, teremos duas
vezes o 180º, perfazendo um total de 360º. Assim sendo, a soma dos ângulos internos de qualquer
quadrilátero e sempre 360º.
Usando essa informação podemos descobrir a medida do ângulo
desconhecido no quadrilátero à esquerda. Para tanto devemos saber
que a medida do ângulo desconhecido é o que falta para completar
360º.
Sendo assim, calcule.
1- O polígono desenhado na figura é um
pentágono e está dividido em 3
triângulos. Qual é a soma das medidas
dos ângulos internos do pentágono?
2- Calcule o valor de x nos quadriláteros.
3- Calcule o valor de x na figura.
6

EXERCÍCIOS COMPLEMENTARES
1- Um triângulo pode ter os ângulos medindo:
a) 70º, 70º e 70º b) 75º, 85º e 20º c) 75º, 85º e 25º d) 70º, 90º e 25º
2- 72º é a medida do:
a) suplemento de um ângulo de 98º. b) complemento de um ângulo de 98º.
c) suplemento de um ângulo de 108º. d) complemento de um ângulo de 108º.
3- O complemento e o suplemento do ângulo de 57º30’ medem, respectivamente:
a) 90º e 180º b) 180º e 90º c) 32º30’ d) 122º30’ e 32º30’
4- O complemento de um ângulo x mede 12º. O suplemento de x mede:
a) 12º b) 22º c) 102º d) 122º
5- A diferença entre os ângulos dos ponteiros de um relógio que marca 2h30min e de outro que marca 1h é de:
6- Quanto mede o ângulo y?
a) 50º
b) 80º
c) 70º
d) 130º
7

7- (Saresp – SP) Na figura abaixo o triângulo AMN é
eqüilátero.
Então podemos dizer que a medida x do ângulo DCN é:
a) 30º b) 45º
c) 60º d) 70º
8- (UF – MA) Dois ângulos opostos pelo vértice medem 3x + 10º e x + 50º. Um deles mede:
a) 20º b) 30º c) 70º d) 80º
8- O valor de x na figura é:
a) 27º30’ b) 28º45’ c) 30º30’ d)33º45’
9- A medida x do ângulo assinalado na figura abaixo é igual a:
a) 133º b) 132º c) 118º d) 125º
10- Na figura, DE é paralelo a BC. O valor de x é:
a) 90º b) 80º c) 70º d) 60º
8

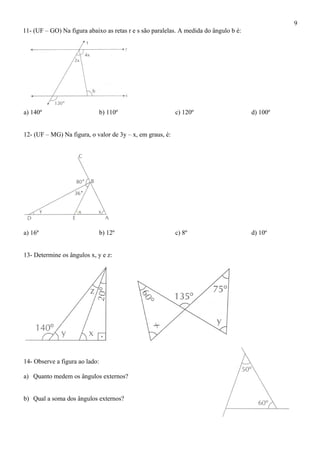
11- (UF – GO) Na figura abaixo as retas r e s são paralelas. A medida do ângulo b é:
a) 140º b) 110º c) 120º d) 100º
12- (UF – MG) Na figura, o valor de 3y – x, em graus, é:
a) 16º b) 12º c) 8º d) 10º
13- Determine os ângulos x, y e z:
14- Observe a figura ao lado:
a) Quanto medem os ângulos externos?
b) Qual a soma dos ângulos externos?
9

15- Sabendo que r // s, calcule x e y.
16- Responda:
a) O que é um triângulo eqüilátero?
b) O que é um triângulo isósceles?
c) Como são os ângulos de um triângulo isósceles?
d) Num triângulo isósceles há um ângulo reto. Quanto medem os outros dois?
17- Os triângulos seguintes são isósceles. Qual o valor dos ângulos indicados com letras?
18- Na figura, a reta assinalada é um eixo de
simetria do triângulo. Obtenha os ângulos
indicados com letras.
19- Na figura, o triângulo ABC é eqüilátero e o
triângulo ACD é isósceles (AC = CD). Qual a
medida do ângulo x?
10

6- ÂNGULOS DE UM POLÍGONO
Sempre tomando como suporte os triângulos, podemos calcular a soma dos ângulos internos de qualquer
polígono, seja ele regular ou não. A seguir, veremos como isso acontece de forma muito simples.
1) Vamos desenhar um polígono qualquer.
2) Traçamos as diagonais que partem do mesmo lado para que possamos determinar vários triângulos.
Nesse caso, como podemos observar, conseguimos 4 triângulos.
Assim sendo, podemos aproveitar o que já sabemos, ou seja, que a
soma dos ângulos internos de qualquer triângulo e sempre 180º. Basta
verificar quantos triângulos o polígono dentro de si e multiplicar por 180º.
Então temos:
4 . 180º = 720º
3) Veja algumas situações interessantes:
Consideremos n, o número de lados de um polígono e t o número de triângulos que podem ser formados
pelas diagonais que partem somente de um vértice desse polígono.
n = 3  t = 1 n = 4  t = 2 n = 5  t = 3 n = 6  t = 4 n = 7  t = 5
Podemos verificar que se compararmos o número de lados com o número de triângulos internos nesses
polígonos, constataremos que sempre ocorre uma diferença constante igual a 2, ou seja, o número de
triângulos é sempre dois a menos que a quantidade de lados. Se o polígono possui 10 lados, teremos 8
triângulos; se possui 20 lados, 18 triângulos; se possui 23 lados, 21 triângulos, etc..
Partindo desse ponto de vista, podemos formar uma lei geral de formação para qualquer polígono.
Veja:
n  número de lados
t  número de triângulos
Sn soma dos ângulos internos do polígono
Sn = (n – 2) . 180º
11

1- Calcule a soma dos ângulos internos de:
a) um octógono;
b) um polígono de 11 lados;
c) um polígono de 15 lados;
e) um polígono de 20 lados.
2- A soma dos ângulos internos de um polígono é 900º. Qual é o polígono?
3- Determine todos os ângulos de cada polígono.
a) Triângulo, um ângulo de 50º e outro de 60º.
b) Quadrilátero, dois ângulos de 80º e outro de 70º.
c) Pentágono, dois ângulos de 105º e outros três congruentes.
d) Hexágono, seis ângulos congruentes.
Revisando
1- Sabendo que r // s, determine os ângulos indicados pelas letras.
2- Na figura, os três polígonos são regulares.
12

Calcule mentalmente o valor de a.
3- Desafios.
A) Na figura, o pentágono é um polígono regular. Determine os ângulos indicados na figura.
B) Se as retas r e s são paralelas, determine os ângulos x, y e z indicados.
r
r
s
s
C) (Uniube – MG) Considere a figura abaixo em que as retas p e q são paralelas e as retas r e s são
perpendiculares. Qual a medida, em graus, do ângulo x?
a) 144º b) 126º c) 136º d) 104º
D)(Fundação Carlos Chagas – SP) Na figura abaixo tem-se r // s; t e u são transversais. O valor de x + y é:
a) 100º b) 120º c) 130º d) 140º
E) (Cesgranrio – RJ) As retas r e s da figura são paralelas cortadas pela transversal t. Se o ângulo B é o
triplo de A, então B – A vale:
a) 75º b) 80º c) 85º d) 90º
7- CÍRCULO, CIRCUNFERÊNCIA E CILINDRO
13

 Circunferência é a linha formada por todos os pontos que distam de um ponto fixo, que é chamado
centro da circunferência.
 Círculo é a superfície ocupada por essa circunferência.
 Cilindro é um sólido geométrico formado por bases que são círculos paralelos e um corpo retangular.
As fórmulas que utilizaremos são:
Comprimento da circunferência  C = 2 . π . r
π é uma constante matemática que vale aproximadamente 3,14
r representa o tamanho do raio.
área do círculo  A = π . r²
 área total do cilindro  AT = 2 . (π . r²) + b . h
 volume do cilindro  Vc = Ab . h
1- A altura de uma árvore é 7 m. Será fixada uma escada a 1 m de sua base para que um homem possa
podar seus galhos. Qual o menor comprimento que esta escada deverá ter?
27d)25c)34b)32)a
2- Na figura, os vértices do quadrado ABCD estão sobre uma circunferência de centro O. Se o lado desse
quadrado mede 3 cm, o raio da circunferência, em centímetros, é dado por:
14

2
3
2
23
c)23b)33)a
3- Uma lata em forma de um cilindro tem 20 cm de altura e sua base é um círculo de raio igual a 6 cm. A
área do papel necessário para cobrir toda a superfície dessa lata, incluindo a tampa e o fundo, é de
aproximadamente:
(Dado: Área do círculo A = πr², com π = 3,14)
a) 751 cm² b) 867 cm² c) 936 cm² d) 980 cm²
4- Observe o paralelepípedo retângulo da figura, e assinale a afirmativa correta:
a) a aresta AD é paralela à aresta BG.
b) as faces ABCD e EFGH são perpendiculares entre si.
c) a aresta EF é perpendicular à aresta DE.
d) as faces ABGF e ABCD são paralelas entre si.
5- Calcule o lado de um quadrado inscrito em uma circunferência de raio 6 cm.
7- Calcule a apótema de um quadrado inscrito numa circunferência de raio 85 .
8- O lado de um quadrado inscrito em uma circunferência mede 210 . Calcule o raio da circunferência.
9- Qual é o perímetro de um hexágono regular inscrito em uma circunferência de 12 cm de diâmetro?
10- Qual a medida do lado de um quadrado inscrito em uma circunferência de 6 m de diâmetro?
ÁREA DE POLÍGONOS
15

1- Calcule a área da região sombreada, supondo as medidas em cm.
16

2- Na figura, calcule;
a) a área do quadrado menor.
b) a área do quadrado maior.
c) a área da região sombreada.
3- A área do trapézio da figura abaixo mede 42 cm² e sua altura 3 cm. Calcule o valor de x.
4- O perímetro do losango abaixo é de 40 cm. Calcule a área desse losango.
17

Alguns tópicos de geometria

Mais conteúdo relacionado

Mais procurados (20)

Destaque (20)

Semelhante a Alguns tópicos de geometria (20)

Mais de Colégio Olavo Hansen- Mauá - São Paulo (15)

Último (20)

Alguns tópicos de geometria