Estimación de caudales máximos

ESTIMACIÓN DE CAUDALES MÁXIMOS EN CUENCAS SIN INFORMACIÓN Manuel E. García-Naranjo B. Septiembre 2011

INTRODUCCION La estimación de caudales máximos asociados a determinados periodos de retorno de diseño es fundamental en muchas aplicaciones de la Ingeniería Hidráulica. En la determinación de valores extremos normalmente se estará en alguno de los siguientes escenarios: Caso de un río con registros de Qmax Caso de un río sin información de Qmax

INTRODUCCION El primero de los casos normalmente se aborda haciendo uso de las distribuciones probabilísticas más usuales: Normal Log Normal de 2 Parámetros Log Normal de 3 Parámetros Gamma de 3 Parámetros o Pearson tipo III Log Gamma de 3 Parámetros o Log Pearson tipo III Gumbel viendo de emplear la distribución de mejor ajuste de acuerdo a los resultados obtenidos a partir de pruebas como Chi-Cuadrado o Kolmogorov-Smirnov.

INTRODUCCION En el segundo caso, al no contarse con estaciones de aforo que proporcionen registros de descargas máximas, se tendrá que acudir a métodos alternativos, basados la mayoría de ellos en datos de precipitación máxima en 24 horas y en las características físicas de la cuenca, para así inferir los caudales máximos asociados a un cierto periodo de retorno que podrían presentarse en la zona de interés de un proyecto en estudio.

INTRODUCCION El presente artículo pretende efectuar un breve repaso de los métodos más usuales disponibles para la estimación de Qmax, tales como: Fórmula racional Método de la envolvente de descargas máximas de Creager Método del hidrograma unitario triangular Método “B” del Estudio de la Hidrología del Perú Método del Sistema DIPEO de Electrificación Rural

FÓRMULA RACIONAL El caudal se expresa como: donde: Q: caudal de diseño, correspondiente al periodo de retorno seleccionado, en m 3 /s C: coeficiente de escorrentía i: intensidad de la lluvia de diseño, en mm/h A: área de la cuenca, en Ha

FÓRMULA RACIONAL El Coeficiente de Escorrentía, C: El valor del coeficiente de escorrentía depende de diversos factores: Permeabilidad de la superficie Pendiente y características de encharcamiento de la superficie (almacenamiento de depresión) Características y condiciones del suelo (humedad antecedente, compactación, porosidad, posición del nivel freático) Vegetación

FÓRMULA RACIONAL Según Aparicio (1999)

FÓRMULA RACIONAL Según Benitez et al. (1980)

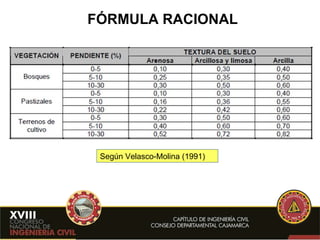
FÓRMULA RACIONAL Según Velasco-Molina (1991)

FÓRMULA RACIONAL Según Chow et al. (1988)

FÓRMULA RACIONAL La Intensidad de Lluvia, i: El valor de la intensidad de lluvia de diseño se obtiene de las curvas intensidad-duración-frecuencia para una duración igual al tiempo de concentración de la cuenca y para una frecuencia correspondiente al periodo de retorno seleccionado (*). La intensidad de lluvia también puede ser determinada a partir del método sugerido por el U.S. Soil Conservation Service, considerando alguno de los perfiles de lluvia estándar. (*) ver ponencia Curvas Intensidad-Duración-Frecuencia, Manuel García-Naranjo, XVII Congreso Nacional de Ingeniería Civil, Lambayeque, 2009

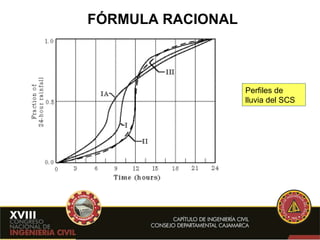
FÓRMULA RACIONAL Perfiles de lluvia del SCS

FÓRMULA RACIONAL Normalmente la fórmula racional tiene aplicación para cuencas pequeñas, de hasta 10 ó 20 km 2 según señalan algunos autores. Ello hace de este método un procedimiento ideal para la determinación del caudal Qmax en el diseño de sistemas de drenaje pluvial o en el proyecto de las obras de drenaje de carreteras. Cuando se aplica la fórmula racional a cuencas de mayor tamaño, usualmente se obtiene valores del caudal bastante elevados.

MÉTODO DE CREAGER Este método, originalmente desarrollado por Creager, fue adaptado para el territorio peruano por Wolfang Trau y Raúl Gutiérrez Yrigoyen. La aplicación de este método permite la estimación de los caudales máximos diarios en cuencas sin información, para diferentes periodos de retorno, tomando el área de la cuenca como el parámetro de mayor incidencia en la ocurrencia de caudales máximos.

MÉTODO DE CREAGER La fórmula empleada es la siguiente: donde: Qmax: caudal máximo para un periodo de retorno T seleccionado, en m 3 /s A: área de la cuenca aportante, en km 2 T: periodo de retorno, en años C 1 , C 2 : coeficientes adimensionales de escala, por regiones hidráulicas m, n: exponentes adimensionales, por regiones hidráulicas

MÉTODO DE CREAGER Según los autores, el territorio peruano queda subdividido en siete regiones hidráulicas diferenciables, tal como se muestra en el mapa:

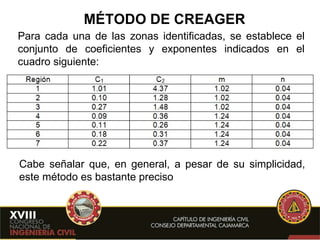
MÉTODO DE CREAGER Para cada una de las zonas identificadas, se establece el conjunto de coeficientes y exponentes indicados en el cuadro siguiente: Cabe señalar que, en general, a pesar de su simplicidad, este método es bastante preciso

MÉTODO DEL H.U. TRIANGULAR Este método fue originalmente desarrollado por Mockus y posteriormente adoptado por el Soil Conservation Service (S.C.S.). Proporciona los parámetros fundamentales del hidrograma, como son: caudal pico (Q p ); tiempo base (t b ) y tiempo en el que se produce el pico (t p ).

MÉTODO DEL H.U. TRIANGULAR Del análisis de varios hidrogramas, Mockus concluyó que el tiempo base y el tiempo pico se relacionan mediante la expresión: t b = 2.67 t p con lo cual, Q p se escribe como: donde: Q p - caudal máximo o pico, en m 3 /s A - área de la cuenca, en Km 2 Pe - altura de precipitación en exceso, en mm t p – tiempo pico, en hr t b - tiempo base, en hr

MÉTODO DEL H.U. TRIANGULAR El tiempo pico se expresa como: donde: t p - tiempo pico, en hr t r - tiempo de retraso, en hr d e - duración en exceso, en hr

MÉTODO DEL H.U. TRIANGULAR La duración en exceso, d e , se puede calcular aproximadamente con alguna de las siguientes relaciones: para cuencas grandes: para cuencas pequeñas: d e = t c Alternativamente, d e puede también determinarse con la expresión: donde: d e - duración en exceso, en hr t c - tiempo de concentración, en hr

MÉTODO DEL H.U. TRIANGULAR El tiempo de retraso, t r , se puede estimar mediante las siguientes expresiones: a) tr = 0.6 tc b) Según Chow: donde: t r - tiempo de retraso, en hr t c - tiempo de concentración, en hr L - longitud del cauce principal, en m S - pendiente del cauce, en %

MÉTODO DEL H.U. TRIANGULAR La precipitación en exceso se determina mediante el siguiente procedimiento: Calcular la Pmax en 24 hr para el periodo de retorno seleccionado Calcular la lámina de lluvia para la duración d e . Se puede hacer uso de la expresión de Dyck y Peschke (1978), la cual permite estimar la lámina (P) e intensidad de lluvia para cualquier duración D (en minutos) en función de la precipitación máxima en 24 hr.

MÉTODO DEL H.U. TRIANGULAR Determinar la precipitación efectiva o lluvia en exceso, P e , mediante el método del S.C.S.: donde: ; Ia = 0.20 S En las expresiones anteriores: Pe - precipitación efectiva, en pulgadas P - precipitación de diseño, en pulgadas S - abstracción inicial CN - número hidrológico o número de curva

MÉTODO DEL ESTUDIO DE LA HIDROLOGIA DEL PERÚ De acuerdo con este planteamiento, descrito en la Parte II – Escorrentía, del Volumen III del Estudio de la Hidrología del Perú, documento elaborado en la década del 80 por el IILA-Senamhi-UNI, se define: S – superficie de la cuenca Q – valor máximo anual de los caudales máximos de avenidas u – rendimiento máximo de la cuenca en avenidas. En particular, u(10) y u(20) representan el rendimiento de la cuenca para avenidas con periodos de retorno de 10 y 20 años respectivamente.

MÉTODO DEL ESTUDIO DE LA HIDROLOGIA DEL PERÚ El método efectúa un agrupamiento de cuencas hidrológicamente similares. Para las estaciones asociadas a cada grupo, los valores de u(10) y u(20) han sido determinados como parte del Estudio. Se establece entonces las siguientes regresiones: log(S) vs log(u(10)) log(S) vs log(u(20)) con lo que, para una cuenca cualquiera de área S, se puede determinar los correspondientes valores de u(10) y u(20).

MÉTODO DEL ESTUDIO DE LA HIDROLOGIA DEL PERÚ El conocimiento de u(10) y u(20) permite calcular los valores de Qmax(10) y Qmax(20). Al plotearse en papel probabilístico Gumbel o al aplicar las relaciones vinculadas a la distribución Gumbel, es posible determinar entonces el valor de Qmax correspondiente a la cuenca en estudio, para cualquier periodo de retorno.

MÉTODO DEL ESTUDIO DE LA HIDROLOGIA DEL PERÚ

MÉTODO DEL SISTEMA DIPEO El método al que se hace referencia es el desarrollado por el Instituto ORSTOM (Francia), el cual fue seleccionado por el Convenio GTZ-EletroPerú en la elaboración del Sistema DIPEO para la Electrificación Rural del Perú, 1990 (ver Libro P, Vol 3, Tomo I). De acuerdo con este método, el caudal de avenidas extraordinarias en cuencas hidrográficas de 1 km 2 a 200 km 2 puede determinarse mediante la siguiente ecuación:

MÉTODO DEL SISTEMA DIPEO Q = P(24h) * A * C R * C P/R * C F / T c donde: P(24h): precipitación máxima diaria, en mm, correspondiente a un periodo de retorno seleccionado A: área de la cuenca, en km 2 . C R : coeficiente de reducción, según el área de la cuenca Los valores de C R se obtienen del siguiente cuadro: Area de la Cuenca (Km 2 ) Coeficiente C R 0  A ≤ 25 1.0 25  A ≤ 50 0.95 50  A ≤ 100 0.90 100  A ≤ 150 0.85 150  A ≤ 200 0.80

MÉTODO DEL SISTEMA DIPEO C P/R – coeficiente de reducción según la permeabilidad y pendientes longitudinal y transversal de la cuenca El coeficiente C P/R se determina con el auxilio de gráficos que dependen de: Condiciones climatológicas: Tropicales y tropicales de transición ó Mediodesiertos y Sahara Permeabilidad de la cuenca: P1: terreno totalmente impermeable, rocoso y/o arcilloso P2: terreno casi impermeable, con muy reducidas zonas de permeabilidad P3: terreno todavía impermeable, con pequeñas zonas de permeablidad P4: terreno bastante permeable; por ejemplo, zonas con granito y arena P5: zonas totalmente permeables, con arena, rocas y profundas grietas. Pendiente de la cuenca: R2: pendiente menor o igual a 0.5% R3: pendiente entre 0.5% y 1.0% R4: pendiente entre 1.0% y 2.0% R5: pendiente mayor a 2%

MÉTODO DEL SISTEMA DIPEO C F – coeficiente que considera la forma de la curva del caudal . El coeficiente C F se obtiene del siguiente cuadro, en función de la precipitación prevaleciente y del área de la cuenca:

MÉTODO DEL SISTEMA DIPEO T c – tiempo de concentración de la cuenca, en segundos. El mismo puede ser determinado mediante los métodos usuales o con el auxilio de los gráficos suministrados por el presente método, en función del área y de la pendiente de la cuenca. La única limitación de este métodos es que los resultados tienen mayor confiabilidad para cuencas pequeñas o medianas, no mayores a 200 km 2 en extensión.

CONCLUSIONES Los métodos presentados son de total aplicabilidad en las cuencas peruanas; más aún, al menos dos de ellos han sido desarrollados tomando en consideración la realidad de nuestro territorio. En el estudio de proyectos reales, es recomendable hacer uso de varios de los métodos presentados y luego, analizar los resultados obtenidos; momento en el cual, la experiencia del especialista resulta esencial.

Estimación de caudales máximos

Más contenido relacionado

La actualidad más candente (20)

Similar a Estimación de caudales máximos (20)

Más de Manuel García Naranjo B. (16)

Último (20)

Estimación de caudales máximos