O CÍRCULO E O NÚMERO Pi
- 1. TAREFA DA SEMANA 2 Aluno: Marco Antônio do Nascimento Nunes – Polo D.Caxias
- 2. O CÍRCULO E O NÚMERO (Pi)
- 3. INTRODUÇÃO O círculo é uma figura geométrica muito comum em nosso cotidiano. É possível encontrarmos diversos objetos circulares a nossa volta tais como: moedas, discos, mesa de refeição, dentre outros. Quando falamos em círculo, ninguém tem dúvida quanto ao formato dessa figura geométrica. No entanto, em geometria, costuma-se fazer uma pequena distinção entre círculo e circunferência, sobre a qual você já deve ter ouvido falar. A superfície de uma moeda, de uma pizza ou de um disco é um círculo. Pensaremos agora, na possibilidade de unirmos todos os pontos do contorno destes objetos, partindo de um mesmo ponto (centro da circunferência), quando fazemos isso, estamos diante do que chamamos de circunferência. E o raio da circunferência seria a distância do centro da circunferência a um ponto do contorno do objeto.
- 4. OBJETIVOS Diferenciar círculo de circunferência. Reconhecer a relação existente entre, o comprimento e o diâmetro, de uma circunferência. Valorizar o pensamento matemático através da história da matemática .
- 5. METODOLOGIA E APRESENTAÇÃO DE MATERIAIS Vejamos algumas definições importantes:
- 6. CIRCUNFERÊNCIA É o lugar geométrico dos pontos de um plano, eqüidistantes de um ponto fixo chamado centro.
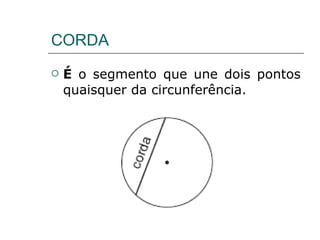
- 7. CORDA É o segmento que une dois pontos quaisquer da circunferência.
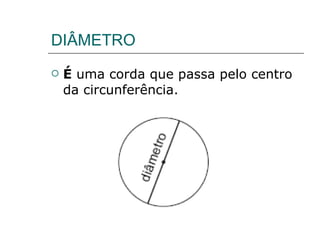
- 8. DIÂMETRO É uma corda que passa pelo centro da circunferência.
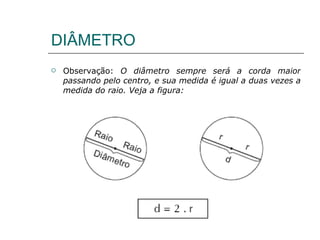
- 9. DIÂMETRO Observação: O diâmetro sempre será a corda maior passando pelo centro, e sua medida é igual a duas vezes a medida do raio. Veja a figura:
- 10. CÍRCULO É Superfície plana limitada por uma circunferência
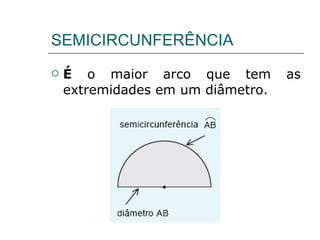
- 11. SEMICIRCUNFERÊNCIA É o maior arco que tem as extremidades em um diâmetro.
- 12. DESCOBRINDO UMA RELAÇÃO Se nos diferentes objetos com formas circulares encontrados em nosso dia-a-dia, medirmos os comprimentos das suas circunferências (das bordas) e de seus diâmetros. Será possível estabelecer uma relação entre essas medidas? Mostraremos a seguir uma atividade envolvendo recursos simples capazes de fornecer com boa aproximação desta relação:
- 13. ATIVIDADE EXPERIMENTAL Pegue uma tampa plástica de uma lata (NESCAU); Com o auxílio de uma régua, meça o seu diâmetro, e anote a medida obtida na tabela abaixo; Com o auxílio de uma tesoura, recorte a sua borda; Com o auxílio de uma régua, meça o comprimento da circunferência, e anote a medida obtida na tabela abaixo; DIÂMETRO (d)COMP. DA CIRCUNFERÊNCIA (C)VALOR OBTIDO (C/d) VALOR OBTIDO (C/d) COMP. DA CIRCUNFERÊNCIA (C) DIÂMETRO (d)
- 14. O COMPRIMENTO DA CIRCUNFERÊNCIA Quanto maior for o raio (ou o diâmetro) de uma circunferência, maior será o seu comprimento. É fácil perceber isso, se na atividade anterior ao invés de uma, usássemos três tampas circulares de tamanhos variados, verificaríamos que o valor obtido, aproxima-se de um mesmo valor (constante), mostrando assim, que o comprimento e o diâmetro da circunferência são grandezas diretamente proporcionais.
- 15. O COMPRIMENTO DA CIRCUNFERÊNCIA A atividade do slide anterior, permite verificar experimentalmente, que quando é aumentada a medida do comprimento da circunferência, também é aumentado o seu diâmetro na mesma proporção. Obs: Ao dividir a medida do comprimento da circunferência pela medida de seu diâmetro, encontraremos sempre um número um pouco maior do que 3. Na realidade, esse número é sempre o mesmo e vale aproximadamente 3,14. Da mesma forma que nossas medições são aproximadas, o resultado das divisões também é uma aproximação. Esse número tão útil e importante é chamado de pi e simbolizado pela letra grega π. Conclusão