Funcoes nas Ciências e no dia a dia
- 1. C531.A UTILIZAÇÃO DAS TIC NOS PROCESSOS DE ENSINO / APRENDIZAGEM 2014-2015 Formanda Maria José Borges Dias da Silva Formadores: Elvira Rodrigues Vítor Santos As Funções Origem, aplicações na Ciências e a ligação ao dia a dia
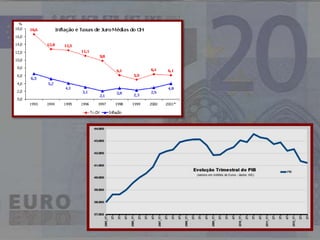
- 2. O Homem procura conhecer os fenómenos naturais, sociais, económicos e culturais que o rodeiam e interpretá-los, e estabelecer leis que os regem. Na generalidade das situações essas leis são descritas pelas funções. Introdução
- 3. Nas Ciências A sua origem No dia a dia FUNÇÕES
- 5. Física
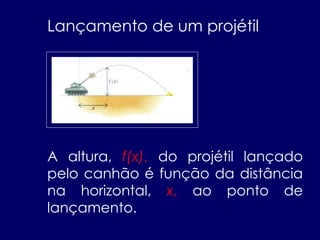
- 6. A altura, f(x), do projétil lançado pelo canhão é função da distância na horizontal, x, ao ponto de lançamento. Lançamento de um projétil
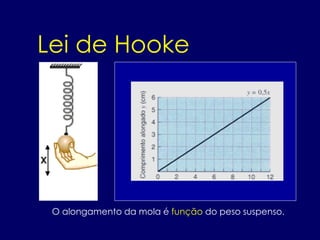
- 8. O alongamento da mola é função do peso suspenso. Lei de Hooke
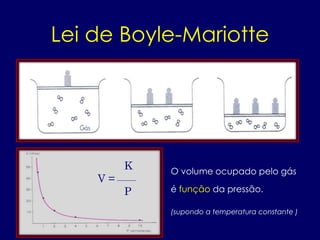
- 9. O volume ocupado pelo gás é função da pressão. (supondo a temperatura constante ) K V = P Lei de Boyle-Mariotte
- 10. Arquimedes
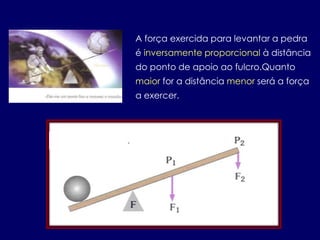
- 11. A força exercida para levantar a pedra é inversamente proporcional à distância do ponto de apoio ao fulcro.Quanto maior for a distância menor será a força a exercer.
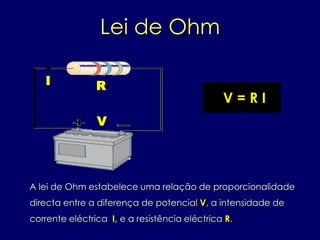
- 12. Lei de Ohm A lei de Ohm estabelece uma relação de proporcionalidade directa entre a diferença de potencial V, a intensidade de corrente eléctrica I, e a resistência eléctrica R. V = R I V I R
- 17. Arquitetura
- 18. Pelas suas propriedades físicas , estéticas e refletoras os arcos de parábolas e hipérboles surgem na Arquitetura em: Pontes Arcos Pórticos
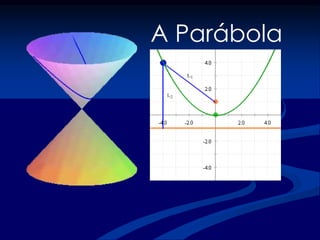
- 19. A Parábola
- 20. Golden Gate Bridge Arcos de água Colégio Teresiano
- 21. Propriedade Refletora da Parábola Farol de automóvel Todo o raio luminoso que incide num espelho parabólico passando pelo foco reflete-se paralelamente ao eixo. Antena Parabólica
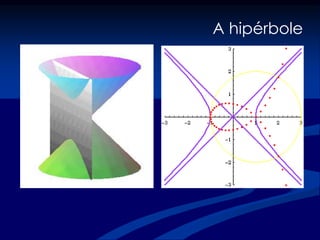
- 22. A hipérbole
- 24. As funções no dia a dia
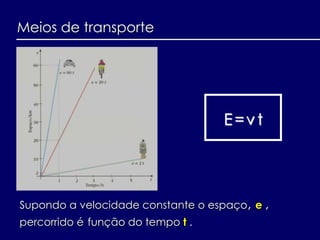
- 25. Meios de transporte Supondo a velocidade constante o espaço, e , percorrido é função do tempo t . E=v t
- 26. Preços O desconto ,y, obtido pelos clientes é diretamente proporcional ao custo inicial ,x, dos produtos. y =0.4 x
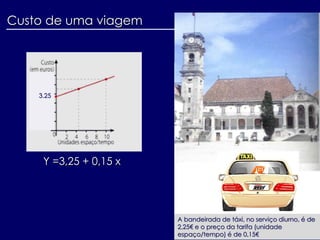
- 27. Custo de uma viagem Y =3,25 + 0,15 x 3.25 A bandeirada de táxi, no serviço diurno, é de 2,25€ e o preço da tarifa (unidade espaço/tempo) é de 0,15€
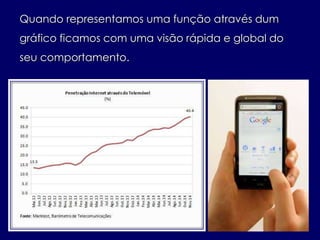
- 28. Quando representamos uma função através dum gráfico ficamos com uma visão rápida e global do seu comportamento.
- 29. Custo de uma chamada telefónica
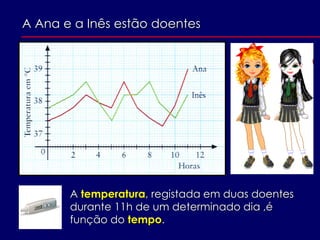
- 30. A Ana e a Inês estão doentes A temperatura, registada em duas doentes durante 11h de um determinado dia ,é função do tempo.
- 32. Uma Introdução Histórica O conceito de função é um dos mais importantes da Matemática. Este conceito sofreu uma grande evolução ao longo dos séculos, sendo que a introdução do método analítico na definição de função (sec., XVI, sec.XVII ) veio revolucionar a Matemática. Desde o tempo dos Gregos até à Idade Moderna a teoria dominante era a Geometria Euclidiana que tinha como elementos base o ponto, a recta e o plano.
- 33. Em fins do século XVI, princípios do século XVII, com os trabalhos de Kepler sobre os movimentos dos planetas e os de Galileu relativos à queda dos graves, a Matemática começa a ser aplicada com êxito ao estudo dos movimentos ( Cinemática e Dinâmica ). A análise matemática surge agora, baseada no conceito de de função. Os seres matemáticos dão-se-nos a conhecer pelas suas variações impressionando os nossos sentidos ; mas também não seria possível conhecê-los, se nessas variações não houvesse uma lei, isto é, uma propriedade ou uma relação sensivelmente constante.
- 34. René Descartes ( França 1596- 1650 ), revolucionou a Matemática e a Ciência ao associar um sistema de eixos, um ponto (P) e um par de números (x,y) que chamou abcissa (x) e ordenada (y) o que permitiu a representação das funções num gráfico. Ora, as leis dos fenómenos são expressas por funções. São pois os conceitos matemáticos de variável e de função que permitem à razão humana interpretar o movimento e, de um modo geral os fenómenos naturais. René Descartes
- 35. Foi Leibniz (1646-1716) ao analisar uma curva à procura de extremos que introduziu o termo função na Matemática. No entanto foi o matemático suiço Euler (17o7-1783) quem utilizou pela primeira vez y = f(x) . Leibniz Assim o conceito de função que hoje nos aparece simples é resultado de uma evolução histórica conduzindo sempre cada vez mais abstração, e que só no século XIX teve o seu final. Euler
- 36. C531.A UTILIZAÇÃO DAS TIC NOS PROCESSOS DE ENSINO / APRENDIZAGEM 2014-2015 Formanda Maria José Borges Dias da Silva Formadores: Elvira Rodrigues Vítor Santos As Funções Origem, aplicações na ciências e a ligação ao dia a dia Obrigada pela atenção!