Do Espaço Ao Plano Unidade 6111
2 gostaram•1,953 visualizações
Este documento fornece informações sobre um plano de aula de matemática do 7o ano. Contém sete temas: 1) Posições relativas de retas e planos, 2) Triângulos, 3) Critérios de igualdade de triângulos, 4) Ângulos, 5) Paralelogramos, 6) Paralelogramos particulares, 7) Áreas e volumes de sólidos. Fornece definições-chave, atividades e exercícios para cada tema.
Do Espaço Ao Plano Unidade 6111
- 1. ESCOLA BÁSICA INTEGRADA ELIAS GARCIA MATEMÁTICA – 7º ANO FICHA INFORMATIVA E DE ACTIVIDADES Unidade 6: Do Espaço ao Plano Nome do Aluno: __________________________________________________Número:_____ Turma:_______ TEMA 1 – POSIÇÕES RELATIVAS DE RECTAS E PLANOS 1
- 2. EXERCÍCIOS SOBRE POSIÇÕES RELATIVAS DE RECTAS E PLANOS 2
- 3. TEMA 2 – TRIÂNGULOS. DESIGUALDADE TRIANGULAR. 3
- 4. DESIGUALDADE TRIANGULAR (REVISÃO 6ºANO) 4
- 5. EXERCÍCIOS SOBRE DESIGUALDADE TRIANGULAR. 5
- 6. CONSTRUÇÃO DE TRIÂNGULOS (REVISÃO 6ºANO) 6
- 7. EXERCÍCIOS SOBRE CONSTRUÇÃO DE TRIÂNGULOS 7
- 8. TEMA 3 – CRITÉRIOS DE IGUALDADE DE TRIÂNGULOS. Dois triângulos são geometricamente iguais quando têm simultaneamente: Os ângulos correspondentes iguais; Os comprimentos dos lados correspondentes iguais. Não é no entanto necessário conhecer todos os elementos de um triângulo (o comprimento dos três lados e a amplitude dos três ângulos) para garantir a igualdade. Existem condições mínimas que garantem a igualdade de dois triângulos – os critérios de igualdade de triângulos. Vais construir alguns triângulos e concluir quais são essas condições mínimas. Abre a página http://matti.usu.edu/nlvm/nav/frames_asid_165_g_3_t_3.html ACTIVIDADE 1 1. Escolhe a opção SSS. 2. Com os três segmentos a vermelho tenta construir um triângulo, unindo as extremidades dos segmentos. - Move um segmento carregando e arrastando o seu ponto médio, utilizando o rato. - Roda um segmento carregando e arrastando uma das extremidades. 3. Quando conseguires formar um triângulo, o seu interior fica colorido. 4. Repete os passos 2 e 3 para os segmentos a azul. 5. Depois de construíres os dois triângulos, sobrepõe um triângulo sobre o outro. O que concluis? ………………………………………………………………… (LLL) CONCLUSÃO: Para que dois triângulos sejam iguais, basta que os três ……………… de um sejam ………………… aos três lados do outro. ACTIVIDADE 2 1. Escolhe a opção SAS. 2. Com os dois segmentos e o ângulo a vermelho tenta construir um triângulo, unindo a um dos segmentos o ângulo e por fim o outro segmento. 3. Quando conseguires formar um triângulo, o seu interior fica colorido. 4. Repete os passos 2 e 3 para os segmentos e o ângulo a azul. 5. Depois de construíres os dois triângulos, sobrepõe um triângulo sobre o outro. O que concluis? ………………………………………………………………… (LAL) CONCLUSÃO: Para que dois triângulos sejam iguais basta que dois ……………… sejam iguais e o ……………… compreendido entre eles também seja igual. 8
- 9. ACTIVIDADE 3 1. Escolhe a opção ASA. 2. Com os dois ângulos e o segmento a vermelho tenta construir um triângulo. 3. Quando conseguires formar um triângulo, o seu interior fica colorido. 4. Repete os passos 2 e 3 para os ângulos e o lado a azul. 5. Depois de construíres os dois triângulos, sobrepõe um triângulo sobre o outro. O que concluis? ………………………………………………………………… (ALA) CONCLUSÃO: Para que dois triângulos sejam iguais basta que tenham um ………… igual e os dois ………………… adjacentes a esse lado iguais. EXERCÍCIOS SOBRE CRITÉRIOS DE IGUALDADE DE TRIÂNGULOS 9
- 10. TEMA 4 – ÂNGULOS 10
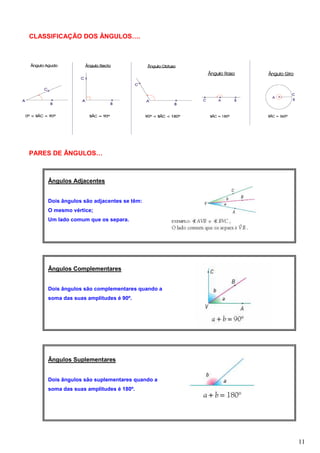
- 11. CLASSIFICAÇÃO DOS ÂNGULOS…. PARES DE ÂNGULOS… Ângulos Adjacentes Dois ângulos são adjacentes se têm: O mesmo vértice; Um lado comum que os separa. Ângulos Complementares Dois ângulos são complementares quando a soma das suas amplitudes é 90º. Ângulos Suplementares Dois ângulos são suplementares quando a soma das suas amplitudes é 180º. 11
- 12. Ângulos Verticalmente Opostos Vamos investigar as relações que existem entre ângulos formados por rectas. Construímos duas rectas, AB e AC, como mostra a figura (o ponto A está em ambas as rectas). As duas rectas concorrentes determinam dois pares de ângulos verticalmente opostos. Ângulos verticalmente opostos são aqueles que têm o mesmo _________________ e em que os ___________ de um estão no prolongamento dos _____________ do outro. D B A E C 1. Assinala com a mesma cor dois ângulos agudos e mede as suas amplitudes. O que verificas? 2. Assinala com outra cor dois ângulos obtusos e mede as suas amplitudes. O que verificas? 3. Os ângulos ∠ BAC e ∠ CAE (um ângulo agudo e um ângulo obtuso ) dizem-se ângulos suplementares. O nome advém do facto de existir uma relação entre eles. Qual é? 4. Conclusão: Ângulos Verticalmente Opostos são___________________________________ Nota: Consulta o endereço: http://moodle.ebiji-eliasgarcia.edu.pt/mod/resource/view.php?id=2122 e faz tu mesmo a experiência com os ângulos assinalados, movendo os seus lados… 12
- 13. Ângulos de Lados Paralelos 1. Construímos a recta AB e o ponto C que não pertence a AB. C A B 2. Depois, construímos a recta paralela a AB que passa por C e a recta AC. C A B 3. Marcamos os pontos D, E, F, G e H como mostra a figura. E D C F H A B G 4.a) Mede os oito ângulos da figura anterior e regista as suas amplitudes: ∠ ECF a sua amplitude é_______ ∠ CAB a sua amplitude é_______ ∠ FCA a sua amplitude é______ ∠ BAG a sua amplitude é_______ ∠ ECD a sua amplitude é________ ∠ CAH a sua amplitude é_______ ∠ DCA a sua amplitude é_______ ∠ HAG a sua amplitude é________. b) Os ângulos ∠ ECF e ∠ CAB dizem-se ângulos de lados paralelos. Escreve todos os pares de ângulos de ângulos de lados paralelos da figura anterior: Agudos:_____________________________________________________________________ O que concluis?_____________________________________________________________________ Obtusos:____________________________________________________________________ O que concluis?_____________________________________________________________________ Um Agudo e Outro Obtuso:_____________________________________________________ O que concluis?_____________________________________________________________________ 13
- 14. 5. Conclusão: Dois ângulos de lados paralelos Se forem da mesma espécie (ambos agudos ou ambos obtusos) são……………………..; Se um for agudo e o outro obtuso, são …………………………………………………………. Nota: Consulta o endereço: http://moodle.ebiji-eliasgarcia.edu.pt/mod/resource/view.php?id=2920 e faz tu mesmo a experiência com os ângulos assinalados, movendo os seus lados… EXERCÍCIOS SOBRE ÂNGULOS 14
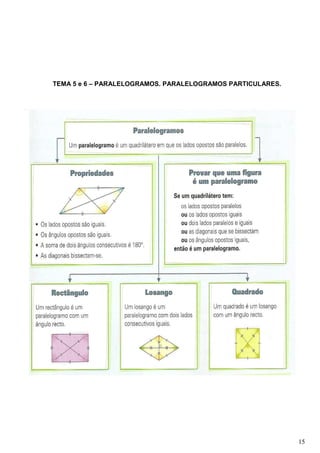
- 15. TEMA 5 e 6 – PARALELOGRAMOS. PARALELOGRAMOS PARTICULARES. 15
- 17. EXERCÍCIOS SOBRE PARALELOGRAMOS PARTICULARES 17
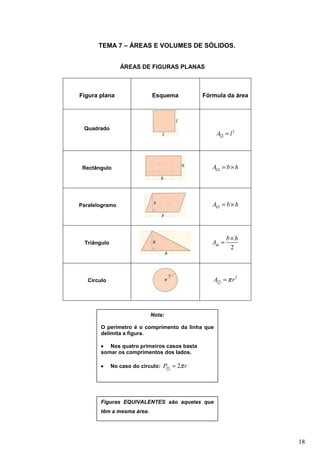
- 18. TEMA 7 – ÁREAS E VOLUMES DE SÓLIDOS. ÁREAS DE FIGURAS PLANAS Figura plana Esquema Fórmula da área Quadrado A□ = l 2 Rectângulo A▭ = b × h Paralelogramo A▱ = b × h b×h Triângulo A△ = 2 Círculo A⊙ = π r 2 Nota: O perímetro é o comprimento da linha que delimita a figura. • Nos quatro primeiros casos basta somar os comprimentos dos lados. • No caso do círculo: P⊙ = 2π r Figuras EQUIVALENTES são aquelas que têm a mesma área. 18
- 19. VOLUMES DE SÓLIDOS PRISMAS CILINDRO Cubo Paralelepípedo Outros prismas V = Ab × h V = Ab × h V = Ab × h ou ou ou V = a3 V = a×b×c V = Ab × h V = π × r2 × h Volume=Área da base × altura PIRÂMIDES CONE Ab × h 1 Ab × h 1 V = ou V = × Ab × h V = ou V = × π × r × h 2 3 3 3 3 1 Volume= × Área da base × altura 3 Sólidos EQUIVALENTES são aqueles que têm o mesmo volume. 19
- 20. EXERCÍCIOS SOBRE ÁREAS E VOLUMES 1 1.1 . 1.2 . 2 2.1 . 2.2 2 3 Bom Trabalho! Professora: Carla Varela 20