Contrução da tabela verdade
- 1. CONTRUÇÃO DA TABELA- VERDADE MATEMÁTICA COMPUTACIONAL ADS FACEMA 1º PERÍODO PROF. ARISTÓTELES MENESES LIMA
- 2. CONSTRUÇÃO DA TABELA-VERDADE Segundo o princípio do terceiro excluído, toda proposição simples é verdadeira (V) ou é falsa (F). Em se tratando de uma proposição composta, a determinação do seu valor lógico, depende unicamente dos valores lógicos das proposições simples componentes.
- 3. DETERMINAÇÃO DO VALOR LÓGICO DA PROPOSIÇÃO COMPOSTA Para determinar o valor lógico de uma proposição composta, recorre-se quase sempre a um dispositivo denominado TABELA-VERDADE. Exemplo: No caso de uma proposição composta cujas proposições simples componentes são p e q, as únicas possíveis atribuições de valores lógicos a p e a q são: p q 1 V V 2 V F 3 F V 4 F F
- 4. Exemplo: No caso de uma proposição composta cujas proposições simples componentes são p, q e r, as únicas possíveis atribuições de valores lógicos a p, a q e a r são: p q r 1 V V V 2 V V F 3 V F V 4 V F F 5 F V V 6 F V F 7 F F V 8 F F F
- 5. OPERAÇÕES LÓGICAS SOBRE PROPOSIÇÕES: Negação (~): Chama-se negação de uma proposição p, a proposição representada por “não p”, cujo valor lógico é a verdade (V) quando p é falsa e a falsidade (F) quando p é verdadeira. “~p” p ~p V F F V
- 6. Conjunção (^): Chama-se de conjunção de duas proposições p e q a proposição representada por “p e q”, cujo valor lógico é (V) quando as proposições p e q são ambas verdadeiras e (F) nos demais casos. (Conjunção = união) “p ^ q” = p e q p q p^q V V V V F F F V F F F F
- 7. Disjunção(V)(ou Disjunção inclusiva): Chama-se de disjunção de duas proposições p e q a proposição representada por “p ou q”, cujo valor lógico é (V), quando ao menos uma das proposições p e q é (V).E a falsidade(F) quando as proposições p e q são ambas falsas. (Disjunção = separação) “p V q” = p ou q p Q pVq V V V V F V F V V F F F
- 8. Disjunção exclusiva ( V ):Chama-se de disjunção exclusiva de duas proposições p e q, cujo valor lógico é a verdade (V) somente quando p é verdadeira ou q é verdadeira, mas não quando p e q são ambas verdadeiras, e a falsidade (F) quando p e q são ambas verdadeiras ou ambas falsas. p q pV q V V F V F V F V V F F F Na linguagem comum a palavra ou tem dois sentidos: o sentido inclusivo e o exclusivo.
- 9. EXEMPLOS P: Carlos é médico ou professor. (disjunção inclusiva - V) Q: Mário é alagoano ou gaúcho. (disjunção exclusiva- V )
- 10. CONDICIONAL ( → ): Chama-se de proposição condicional ou apenas condicional uma proposição representada por “se p então q”, cujo valor lógico é a falsidade (F) no caso em que p é verdadeira e q é falsa e a verdade(V) nos demais casos. “p → q” p Q p→ q V V V V F F F V V F F V
- 11. Uma condicional p → q não afirma que o consequente q se deduz ou é consequência do antecedente p. Sua tabela não é tão óbvia quanto as outras. A condicional significa que a verdade de p implica, ou leva, a verdade de q. Logo, se p é verdadeira e q é falsa, a condicional é falsa. E ainda, a primeira proposição é independente da segunda. p é condição suficiente para q.
- 12. EXEMPLOS “Se Roberto passar no teste de Cálculo, então ele vai ao cinema sexta-feira”. Se Roberto não passar no teste, então - independente de se ele vai ou não ao cinema- você não pode afirmar que a observação é falsa. O que uma condicional afirma é unicamente uma relação entre os valores lógicos das proposições. Não é uma relação de causa e efeito.
- 13. BICONDICIONAL ( ↔ ): Chama-se proposição bicondicional ou apenas bicondicional uma proposição representada por “p se e somente se q”, cujo valor lógico é a verdade(V) quando p e q são ambas verdadeiras ou ambas falsas, e a falsidade (F) nos demais casos. “p ↔ q” p q p↔q V V V V F F F V F F F V
- 14. DETERMINAÇÃO DO VALOR LÓGICO Se p é verdadeiro(V) e r é falso(F), determine o valor lógico de cada proposição: a) p ^ ~r = V ^ V= V b) p v ~r = V v V = V c) ~p ^ r = F ^ F = F d) ~p ^ ~r =F ^ V= F e) ~p v ~r =F v V= V f) p ^ (~p v r) = p ^ (F v F)= V ^ F = F
- 16. EXEMPLO 1 p Q ~q p ^ ~q ~(p ^ ~q) V V F F V V F V V F F V F F V F F V F V
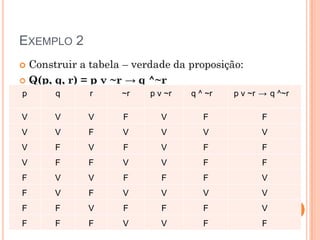
- 17. EXEMPLO 2 p q r ~r p v ~r q ^ ~r p v ~r → q ^~r V V V F V F F V V F V V V V V F V F V F F V F F V V F F F V V F F F V F V F V V V V F F V F F F V F F F V V F F
- 18. EXEMPLO 3: