Aritmetica Computacional
- 1. Aritmética Computacional The complexity is in eye of the observer... As much as the object allows.
- 2. Introdução Humanos: sistema decimal. Computadores: sistema binário. Como representar números negativos e números reais? Qual é o maior número representável numa palavra de computador? O que acontece quando o resultado é maior do que a capacidade do computador?
- 3. Conteúdo Números com sinal e números sem sinal Adição e subtração Operações lógicas Construção de uma unidade aritmética lógica Multiplicação Divisão Operações em ponto flutuante Lendas e falhas Considerações Finais
- 4. Números com sinal e números sem sinal 1
- 5. Números com Sinal e Números sem Sinal Base 10: 2543 (10) =2 10 3 +5 10 2 +4 10 1 +3 10 0 (10) Base 2: 1011 (2) =1 2 3 +0 2 2 +1 2 1 +1 2 0 =11 (10) Representação no Z80 (8 bits) 0 0 0 0 1 0 1 1 Bit Menos Significativo (LSB) Bit Mais Significativo (MSB)
- 6. Faixa de números sem sinal para 8 bits: 0 a 256-1 0000 0000 (2) = 0 (10) 0000 0001 (2) = 1 (10) 0000 0010 (2) = 2 (10) ... 1111 1100 (2) = 252 (10) 1111 1101 (2) = 253 (10) 1111 1110 (2) = 254 (10) 1111 1111 (2) = 255 (10)
- 7. Representação de números Números reais: infinitos. No computador: finitos. Maioria: grande quantidade de zeros à esquerda. Computador: pode lidar com números até um certo tamanho. Overflow : tratado pelo sistema operacional. No computador: é preciso representar números com sinal. Solução: usar 1 bit (sinal magnitude). Primeira tentativa: o bit mais significativos (MSB) é usado para sinal. Problema: duas representações para o zero Solução mais usada: complemento a 2
- 8. Complemento a 2 A regra baseia-se no fato de que a soma de um número com sua representação invertida deve ser -1:
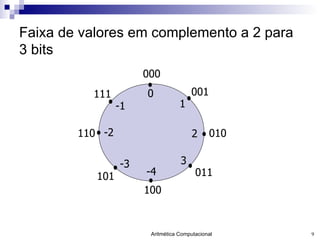
- 9. Faixa de valores em complemento a 2 para 3 bits 0 -4 2 -2 1 3 -3 -1 111 101 011 001 010 110 100 000
- 10. Complemento a 2: regra prática Considere X = 0000 1000, o complemento a 2 de X será: -X = 1111 1000 X = 1111 0111 1 +
- 11. Interface Hardware/Software Endereços: sempre positivos Os números vão de 0 a 27FF (Z80), e não são nunca negativos. Em C: “int” e “unsigned int”.
- 12. Exercícios Converta -15 (10) para binário com representação em sinal/magnitude (16 bits). Converta -15 (10) para binário com representação em complemento a 2 (16 bits). Qual é o número, em decimal, representado em complemento a 2 por 1010 0011 (2) ? Usando complemento a 2 qual é a faixa de números que podem ser representados com 8 bits?
- 13. Adição e Subtração 2
- 14. Adição e Subtração No computador: soma semelhante à soma no sistema decimal. Soma: soma cada bit, mais o vai-um.
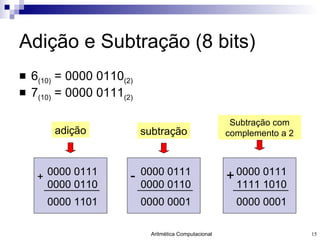
- 15. Adição e Subtração (8 bits) 6 (10) = 0000 0110 (2) 7 (10) = 0000 0111 (2) 0000 0111 0000 0110 + 0000 1101 adição 0000 0111 0000 0110 - 0000 0001 subtração 0000 0111 1111 1010 + 0000 0001 Subtração com complemento a 2
- 16. Overflow Ocorre sempre que o resultado de uma operação não pode ser representado no hardware disponível. Se um número for negativo, e o outro positivo, não ocorrerá overflow. <0 <0 >=0 A-B >=0 >=0 <0 A-B >=0 <0 <0 A+B <0 >=0 >= 0 A+B Resultado Operando B Operando A Operação
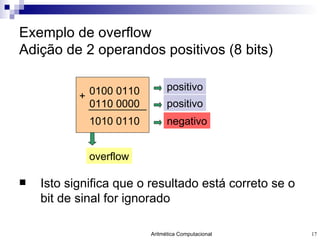
- 17. Exemplo de overflow Adição de 2 operandos positivos (8 bits) Isto significa que o resultado está correto se o bit de sinal for ignorado 0100 0110 0110 0000 + 1010 0110 overflow positivo positivo negativo
- 18. Exemplo de overflow Adição de 2 operandos negativos (8 bits) Isto significa que o resultado é negativo e está em complemento a 2 1000 0000 1010 0000 + 1 0010 0000 overflow negativo negativo positivo carry
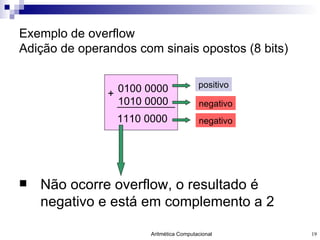
- 19. Exemplo de overflow Adição de operandos com sinais opostos (8 bits) Não ocorre overflow, o resultado é negativo e está em complemento a 2 0100 0000 1010 0000 + 1110 0000 positivo negativo negativo
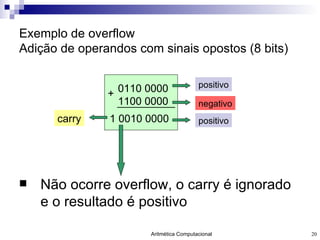
- 20. Exemplo de overflow Adição de operandos com sinais opostos (8 bits) Não ocorre overflow, o carry é ignorado e o resultado é positivo 0110 0000 1100 0000 + 1 0010 0000 positivo negativo positivo carry
- 21. Interface Hardware/Software Na ocorrência de overflow: a máquina precisa decidir como tratá-lo. Linguagem C: não toma conhecimento do overflows. A tarefa é do programador. FORTRAN: trata o overflow
- 22. Exercícios Faça as operações aritméticas abaixo utilizando números binários de 8 bits e complemento a 2: +9 + 4 +9 - 4 -9 + 4 -9 - 4
- 24. Operações Lógicas Em muitas aplicações é necessário processar bits isolados dentro de uma palavra operações lógicas Shifts: deslocamento à esquerda ou à direita instruções rlc, rrc, rl, rr Ver apostila de laboratório: Aula 06 – Instruções de Rotação e Funções
- 25. Operações AND e OR Operação AND: atua bit a bit, deixando 1 como resultado somente no caso de ambos os bits correspondentes dos operandos serem 1 (aplicação de máscara) Operação OR: também atua bit a bit colocando 1 no resultado se qualquer um dos bits correspondentes do operando for 1.
- 26. Construção de uma Unidade Aritmética Lógica 4
- 27. Introdução Representa os músculos do computador: realiza operações aritméticas como a adição e a subtração ou operações lógicas como AND e OR A partir de agora mostrar-se-á como construir uma UAL para realizar as quatro operações acima
- 28. Blocos Construtivos Básicos NOT (Inversora) AND OR Multiplexador Se d==0, c=a senão c=b a c a c b a c b a b 0 1 d c
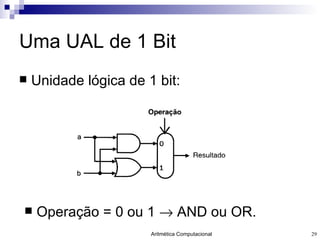
- 29. Uma UAL de 1 Bit Unidade lógica de 1 bit: Operação = 0 ou 1 AND ou OR.
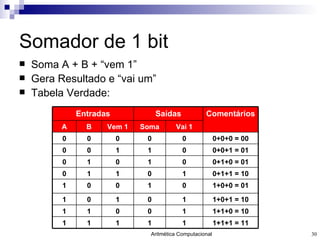
- 30. Somador de 1 bit Soma A + B + “vem 1” Gera Resultado e “vai um” Tabela Verdade: 1+1+1 = 11 1+1+0 = 10 1+0+1 = 10 1+0+0 = 01 0+1+1 = 10 0+1+0 = 01 0+0+1 = 01 0+0+0 = 00 Comentários 1 0 1 1 0 0 1 0 0 1 1 0 1 0 1 1 0 0 1 1 1 0 1 0 Vem 1 1 1 1 1 0 1 1 0 0 1 0 0 0 0 0 0 Vai 1 Soma B A Saídas Entradas
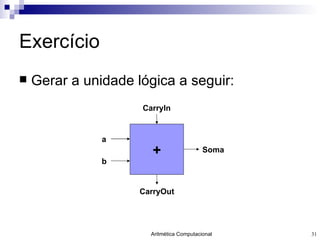
- 31. Exercício Gerar a unidade lógica a seguir: Soma CarryOut CarryIn a b +
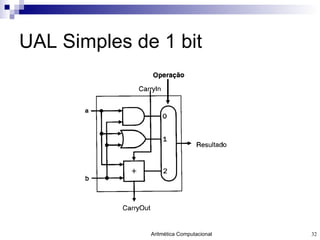
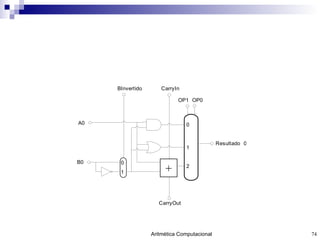
- 32. UAL Simples de 1 bit
- 33. Exercícios Alterar a UAL anterior para que ela gere o valor 0. Dica: a maneira mais fácil é expandir o multiplexador controlado pela linha Operação. Como projetar uma UAL de 32 bits utilizando uma UAL de 1 bit?
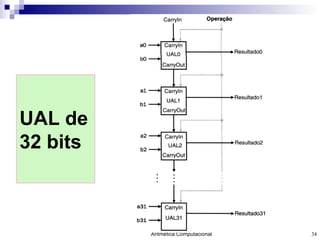
- 34. UAL de 32 bits
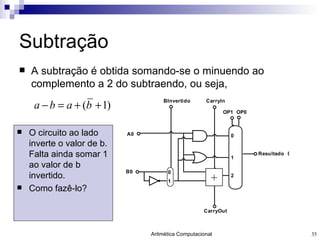
- 35. Subtração A subtração é obtida somando-se o minuendo ao complemento a 2 do subtraendo, ou seja, O circuito ao lado inverte o valor de b. Falta ainda somar 1 ao valor de b invertido. Como fazê-lo?
- 36. Subtração Na soma o primeiro CarryIn (vem 1) é 0. O que acontece de fizermos o primeiro CarryIn = 1?
- 37. Overflow Como fazer a detecção de overflow? Leia o tópico “Adaptação da UAL de 32 bits para o MIPS” e faça o exercício 4.23 do livro texto.
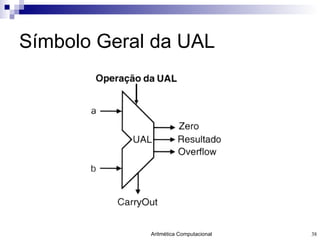
- 38. Símbolo Geral da UAL
- 39. Problema Qual é o problema de uma UAL projetada como a anterior?
- 40. Carry Lookahead Com que velocidade podemos somar dois operandos de 32 bits? Observe que as entradas a e b podem ser perfeitamente determinadas a qualquer tempo, mas a entrada CarryIn de um determinado somador de 1 bit depende do resultado da operação realizada no somador de 1 bit vizinho. Solução: CarryIn1=B0 CarryIn0+a0 CarryIn0+a0 b0 ou C1=b0 c0+a0.c0+a0 b0 C2=b1 c1+a1 c1+a0 b0
- 41. Carry Lookahead Problema deste método: circuito ainda complexo para cálculos de muitos bits e portanto caro. Qual a solução? Método de propagador e gerador. Veja livro texto.
- 42. Multiplicação 5
- 43. Exemplo: como na prática 1000 x 1001 1000 0000 0000 1000____ 1001000 multiplicando multiplicador produto Número de dígitos: multiplicando + multiplicador. 32 bits x 32 bits = 64 bits.
- 44. Algoritmo Como na prática Simplesmente coloque um cópia do multiplicando (1 x multiplicando) no lugar apropriado, se o digito do multiplicando for igual a 1, ou Coloque 0 (0 x multiplicando) no lugar apropriado, se o digito do multiplicando for igual a 0; Veremos a seguir 3 versões do algoritmo de multiplicação para 32 bits (32 x 32 bits)
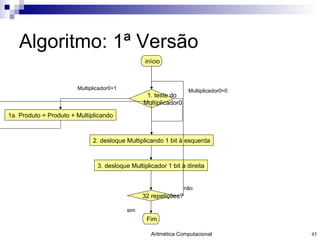
- 45. Algoritmo: 1 ª Versão início 1. teste do Multiplicador0 1a. Produto = Produto + Multiplicando 2. desloque Multiplicando 1 bit à esquerda 3. desloque Multiplicador 1 bit à direita 32 repetições? Fim Multiplicador0=0 Multiplicador0=1 não sim
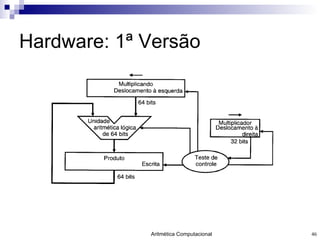
- 46. Hardware: 1 ª Versão
- 47. Exercício Usando números de 4 bits, com o intuito de economizar espaço, multiplique 2 10 por 3 10 ou 0010 2 por 0011 2 . Valores iniciais: Multiplicando = 0000 0010 Multiplicador = 0011 Produto = 0000 0000
- 48. Desvantagens UAL de 64 bits. 2 registradores de 64 bits Próxima versão: Metade dos bits do multiplicando da primeira versão são sempre zero, de modo que somente metade deles poderia conter informações úteis. A segunda versão utiliza-se desta informação para melhorar a performance da multiplicação.
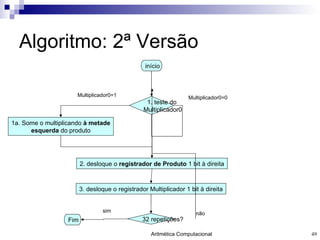
- 49. Algoritmo: 2 ª Versão início 1. teste do Multiplicador0 1a. Some o multiplicando à metade esquerda do produto 2. desloque o registrador de Produto 1 bit à direita 3. desloque o registrador Multiplicador 1 bit à direita 32 repetições? Fim Multiplicador0=0 Multiplicador0=1 não sim
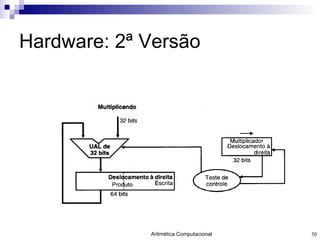
- 50. Hardware: 2 ª Versão
- 51. Exercício Multiplique 0010 2 por 0011 2 usando a segunda versão do algoritmo de multiplicação. Valores iniciais: Multiplicando = 0010 Multiplicador = 0011 Produto = 0000 0000
- 52. Versão Final do Algoritmo de Multiplicação O registrador reservado ao produto desperdiça tanto espaço quanto o do multiplicador: à medida que o desperdício de espaço do produto se reduzia, a mesma coisa acontecia com o multiplicador.
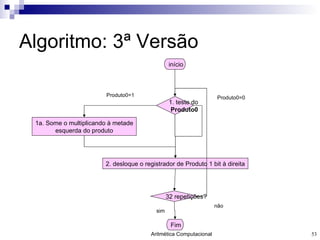
- 53. Algoritmo: 3 ª Versão início 1. teste do Produto0 1a. Some o multiplicando à metade esquerda do produto 2. desloque o registrador de Produto 1 bit à direita 32 repetições? Fim Produto0=0 Produto0=1 não sim
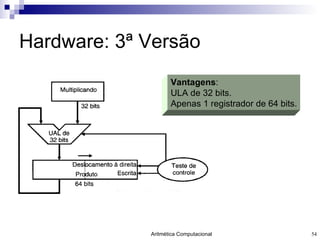
- 54. Hardware: 3 ª Versão Vantagens : ULA de 32 bits. Apenas 1 registrador de 64 bits.
- 55. Exercício Multiplique 0010 2 por 0011 2 usando a terceira versão do algoritmo de multiplicação. Valores iniciais: Multiplicando = 0010 Produto = 0000 0011
- 56. Divisão Divide et impera. Versão latina da velha máxima política “Divida e governe”, citada por Maquiavel em 1532 6
- 57. Divisão A operação recíproca da multiplicação é a divisão, operação que é ainda menos freqüente que a multiplicação e mais ardilosa. Além disso, ela oferece uma rara oportunidade de se efetuar uma operação matemática inválida: a divisão por zero. dividendo = quociente x divisor + resto
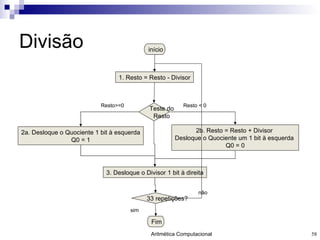
- 58. Divisão início Teste do Resto 2a. Desloque o Quociente 1 bit à esquerda Q0 = 1 3. Desloque o Divisor 1 bit à direita 33 repetições? Fim Resto < 0 Resto>=0 não sim 1. Resto = Resto - Divisor 2b. Resto = Resto + Divisor Desloque o Quociente um 1 bit à esquerda Q0 = 0
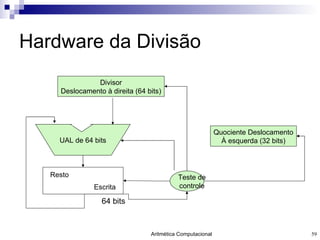
- 59. Hardware da Divisão Divisor Deslocamento à direita (64 bits) UAL de 64 bits Quociente Deslocamento À esquerda (32 bits) Teste de controle 64 bits Resto Escrita
- 60. Exercício Dividir 0000 0111 2 por 0010 2 . Valores iniciais: Quociente = 0000 Divisor = 0010 0000 Resto = 0000 0111
- 61. Operações em Ponto Flutuante 7
- 62. Operações em Ponto Flutuante Suporte a números inteiros com e sem sinal. Suporte a números fracionários: 3,1414, 0,00001 etc. Notação científica: 1,34 x 10 3 . Números normalizados: 1 dígito antes do ponto decimal. Números binários também podem ser normalizados. Ponto decimal / ponto binário. Aritmética com números normalizados: aritmética de ponto flutuante. Em C: “float”. Formato: 1,xxxxxxxx 2 2 yyyy .
- 63. Representação em Ponto Flutuante S – sinal do número F – mantissa, normalizada E – expoente Tamanho: -2,0 10 38 a 2,0 10 38 . s expoente mantissa 32 bits 1 8 23
- 64. Overflow em Ponto Flutuante Ocorre quando o expoente é muito grande pra ser representado pelos 8 bits. Underflow : O módulo do expoente negativo é muito grande. Necessário números maiores: precisão dupla. Na linguagem C: double. Representa números entre -2,0 10 -308 a 2,0 10 308 . s expoente mantissa 64 bits 1 11 52
- 65. Padrão IEEE 754 Torna implícito o “1” à esquerda do ponto binário. Quando o expoente for zero, o hardware não considera o primeiro bit “1” implícito, para permitir a representação do número “0” em ponto flutuante.
- 66. Padrão IEEE 754 Deve permitir comparações rápidas. Seria melhor: o menor coeficiente possível valer 00000000, e o maior 11111111. Modificação: Subtrair 127 (peso) do exponente. Representação de –1: -1+127=-1+01111111=01111110. +1=+1+127=10000000 2 . Formato: Peso para precisão dupla: 1.023.
- 67. Exemplo 1 Representar o número -0,75 10 em ponto flutuante e precisão simples. Representar o número -0,75 10 em ponto flutuante e dupla precisão.
- 68. Resposta da 1 1 a fase: converter para binário: 0,75 x 2 = 1,5 1 0,5 x 2 = 1,0 1 -0,75 10 = -0,11 2 = -0,11 x 2 0 = -1,1 x 2 -1 Em precisão simples: Resultado: Representação:
- 69. Exemplo Converter a palavra abaixo em ponto flutuante para número
- 70. Resposta
- 71. Lendas e Falhas 8
- 72. Lendas e Falhas Lenda: a adição em ponto flutuante é associativa; ou seja, x+(y+z)=(x+y)+z . Lenda: assim como uma instrução de deslocamento à esquerda pode substituir uma multiplicação inteira por uma divisão inteira por uma potência de 2. Lenda: só os matemáticos teóricos se preocupam com a precisão das operações em ponto flutuante.
- 73. Bibliografia Patterson, David A. e Hennessy, John L. Organização e Projeto de Computadores: A Interface Hardware/Software . Ed. LTC, 2. Ed., 2000, Rio de Janeiro.