Apostila matematica apoio.2013-05-29_16-23-39

Apostila de Matemática – oficina 22/05/2013
Trabalhando com material dourado
O Material Dourado Montessori destina-se a atividades que auxiliam o ensino e
a aprendizagem do sistema de numeração decimal-posicional e dos métodos para
efetuar as operações fundamentais (ou seja, os algoritmos).
No ensino tradicional, as crianças acabam "dominando" os algoritmos a partir de treinos
cansativos, mas sem conseguirem compreender o que fazem. Com o Material Dourado a
situação é outra: as relações numéricas abstratas passam a ter uma imagem concreta,
facilitando a compreensão. Obtém-se, então, além da compreensão dos algoritmos, um
notável desenvolvimento do raciocínio e um aprendizado bem mais agradável.
O Material Dourado faz parte de um conjunto de materiais idealizados pela
médica e educadora italiana Maria Montessori.
Maria Montessori dedicou-se à educação de crianças excepcionais, que, graças à
sua orientação, rivalizavam nos exames de fim de ano com as crianças normais das
escolas públicas de Roma. Esse fato levou Maria Montessori a analisar os métodos de
ensino da época e a propor mudanças compatíveis com sua filosofia de educação.
Segundo Maria Montessori, a criança tem necessidade de mover-se com
liberdade dentro de certos limites, desenvolvendo sua criatividade no enfrentamento
pessoal com experiências e materiais. Um desses materiais era o chamado material das
contas que, posteriormente, deu origem ao conhecido Material Dourado Montessori.
Embora especialmente elaborado para o trabalho com aritmética, a idealização deste
material seguiu os mesmos princípios montessorianos para a criação de qualquer um
dos seus materiais, a educação sensorial:
 desenvolver na criança a independência, confiança em si mesma, a
concentração, a coordenação e a ordem;
 gerar e desenvolver experiências concretas estruturadas para conduzir,
gradualmente, a abstrações cada vez maiores;
 fazer a criança, por ela mesma, perceber os possíveis erros que comete ao
realizar uma determinada ação com o material;
 trabalhar com os sentidos da criança.
Inicialmente, o Material Dourado era conhecido como "Material das Contas Douradas"
e sua forma era a seguinte:

Embora esse material permitisse que as próprias crianças compusessem as
dezenas e centenas, a imprecisão das medidas dos quadrados e cubos se constituía num
problema ao serem realizadas atividades com números decimais e raiz quadrada, entre
outras aplicações possíveis para o material de contas. Foi por isso que Lubienska de
Lenval, seguidor de Montessori, fez uma modificação no material inicial e o construiu
em madeira na forma que encontramos atualmente.
O nome "Material Dourado" vem do original "Material de Contas Douradas".
Em analogia às contas, o material apresenta sulcos em forma de quadrados. Pode-se
fazer uma adaptação do material dourado para o trabalho em sala de aula, com papel
quadriculado de 1 cm X 1 cm, onde as peças são feitas da seguinte forma:
unidade dezena centena
(1 X1) (1 X 10) (10 X 10)
SUGESTÃO DE ATIVIDADES - COM MATERIAL DOURADO
1. JOGOS LIVRES
Objetivo : tomar contato com o material, de maneira livre, sem regras.
Durante algum tempo, os alunos brincam com o material, fazendo construções livres. O
material dourado é construído de maneira a representar um sistema de agrupamento.
Sendo assim, muitas vezes as crianças descobrem sozinhas relações entre as peças. Por
exemplo, podemos encontrar alunos que concluem:
- Ah! A barra é formada por 10 cubinhos!
- E a placa é formada por 10 barras!
- Veja, o cubo é formado por 10 placas!
2. MONTAGEM
Objetivo: perceber as relações que há entre as peças.

O professor sugere as seguintes montagens:
- uma barra;
- uma placa feita de barras;
- uma placa feita de cubinhos;
- um bloco feito de barras;
- um bloco feito de placas;
O professor estimula os alunos a obterem conclusões com perguntas como estas:
- Quantos cubinhos vão formar uma barra?
- E quantos formarão uma placa?
- Quantas barras preciso para formar uma placa?
Nesta atividade também é possível explorar conceitos geométricos, propondo desafios
como estes:
- Vamos ver quem consegue montar um cubo com 8 cubinhos? É possível?
- E com 27? É possível?
3. DITADO
Objetivo: relacionar cada grupo de peças ao seu valor numérico.
O professor mostra, um de cada vez, cartões com números. As crianças devem mostrar
as peças correspondentes, utilizando a menor quantidade delas.
Variação:
O professor mostra peças, uma de cada vez, e os alunos escrevem a quantidade
correspondente.
4. FAZENDO TROCAS
Objetivo: compreender as características do sistema decimal.
- fazer agrupamentos de 10 em 10;
- fazer reagrupamentos;
- fazer trocas;
- estimular o cálculo mental.
Para esta atividade, cada grupo deve ter um dado marcado de 4 a 9.
Cada criança do grupo, na sua vez de jogar, lança o dado e retira para si a quantidade de
cubinhos correspondente ao número que sair no dado.
Veja bem: o número que sai no dado dá direito a retirar somente cubinhos.
Toda vez que uma criança juntar 10 cubinhos, ela deve trocar os 10 cubinhos por uma
barra. E aí ela tem direito de jogar novamente.
Da mesma maneira, quando tiver 10 barrinhas, pode trocar as 10 barrinhas por uma
placa e então jogar novamente.
O jogo termina, por exemplo, quando algum aluno consegue formar duas placas.
O professor então pergunta:
- Quem ganhou o jogo?
- Por quê?
Se houver dúvida, fazer as "destrocas".

O objetivo do jogo das trocas é a compreensão dos agrupamentos de dez em dez (dez
unidades formam uma dezena, dez dezenas formam uma centena, etc.), característicos
do sistema decimal.
A compreensão dos agrupamentos na base 10 é muito importante para o real
entendimento das técnicas operatórias das operações fundamentais.
O fato de a troca ser premiada com o direito de jogar novamente aumenta a
atenção da criança no jogo. Ao mesmo tempo, estimula seu cálculo mental. Ela começa
a calcular mentalmente quanto falta para juntar 10, ou seja, quanto falta para que ela
consiga fazer uma nova troca.
* cada placa será destrocada por 10 barras;
* cada barra será destrocada por 10 cubinhos.
Variações:
Pode-se jogar com dois dados e o aluno pega tantos cubinhos quanto for a soma dos
números que tirar dos dados. Pode-se utilizar também uma roleta indicando de 1 a 9.
5. PREENCHENDO TABELAS
Objetivo: os mesmos das atividades 3 e 4.
- preencher tabelas respeitando o valor posicional;
- fazer comparações de números;
- fazer ordenação de números.
As regras são as mesmas da atividade 4. Na apuração, cada criança escreve em uma
tabela a quantidade conseguida.
Olhando a tabela, devem responder perguntas como estas:
- Quem conseguiu a peça de maior valor?
- E de menor valor?
- Quantas barras Lucilia tem a mais que Gláucia?
Olhando a tabela à procura do vencedor, a criança compara os números e percebe o
valor posicional de cada algarismo.
Por exemplo: na posição das dezenas, o 2 vale 20; na posição das centenas vale 200.
Ao tentar determinar os demais colocados (segundo, terceiro e quarto lugares) a criança
começa a ordenar os números.
6. PARTINDO DE CUBINHOS

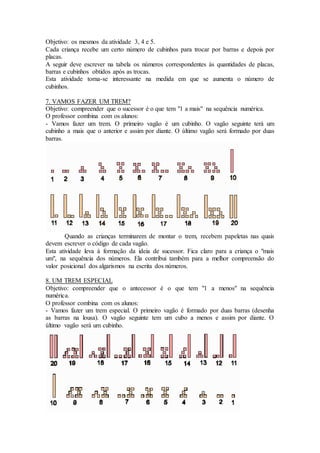
Objetivo: os mesmos da atividade 3, 4 e 5.
Cada criança recebe um certo número de cubinhos para trocar por barras e depois por
placas.
A seguir deve escrever na tabela os números correspondentes às quantidades de placas,
barras e cubinhos obtidos após as trocas.
Esta atividade torna-se interessante na medida em que se aumenta o número de
cubinhos.
7. VAMOS FAZER UM TREM?
Objetivo: compreender que o sucessor é o que tem "1 a mais" na sequência numérica.
O professor combina com os alunos:
- Vamos fazer um trem. O primeiro vagão é um cubinho. O vagão seguinte terá um
cubinho a mais que o anterior e assim por diante. O último vagão será formado por duas
barras.
Quando as crianças terminarem de montar o trem, recebem papeletas nas quais
devem escrever o código de cada vagão.
Esta atividade leva à formação da ideia de sucessor. Fica claro para a criança o "mais
um", na sequência dos números. Ela contribui também para a melhor compreensão do
valor posicional dos algarismos na escrita dos números.
8. UM TREM ESPECIAL
Objetivo: compreender que o antecessor é o que tem "1 a menos" na sequência
numérica.
O professor combina com os alunos:
- Vamos fazer um trem especial. O primeiro vagão é formado por duas barras (desenha
as barras na lousa). O vagão seguinte tem um cubo a menos e assim por diante. O
último vagão será um cubinho.

Quando as crianças terminam de montar o trem, recebem papeletas nas quais
devem escrever o código de cada vagão.
Esta atividade trabalha a ideia de antecessor. Fica claro para a criança o "menos um" na
sequência dos números. Ela contribui também para uma melhor compreensão do valor
posicional dos algarismos na escrita dos números.
9. JOGO DOS CARTÕES
Objetivos: compreender o mecanismo do "vai um" nas adições; estimular o cálculo
mental.
O professor coloca no centro do grupo alguns cartões virados para baixo. Nestes
cartões estão escritos números entre 50 e 70.
1º sorteio: Um aluno do grupo sorteia um cartão. Os demais devem pegar as peças
correspondentes ao número sorteado.
Em seguida, um representante do grupo vai à lousa e registra em uma tabela os números
correspondentes às quantidades de peças.
2º sorteio: Um outro aluno sorteia um segundo cartão. Os demais devem pegar as peças
correspondentes a esse segundo número sorteado.
Em seguida, o representante do grupo vai à tabela registrar a nova quantidade.
Nesse ponto, juntam-se as duas quantidades de peças, fazem-se as trocas e novamente
completa-se a tabela.
Ela pode ficar assim:
Isto encerra uma rodada e vence o grupo que tiver conseguido maior total. Depois são
feitas mais algumas rodadas e o vencedor do dia é o grupo que mais rodadas venceu.
Os números dos cartões podem ser outros. Por exemplo, números entre 10 e 30, na
primeira série; entre 145 e 165, na segunda série.
Depois que os alunos estiverem realizando as trocas e os registros com desenvoltura, o
professor pode apresentar a técnica do "vai um" a partir de uma adição como, por
exemplo, 15 + 16.
Observe que somar 15 com 16 corresponde a juntar estes conjuntos de peças.
Fazendo as trocas necessárias,

Compare, agora, a operação:
* com o material:
*com os números:
Ao aplicar o "vai um", o professor pode concretizar cada passagem do cálculo
usando o material ou desenhos do material, como os que mostramos.
O "vai um" também pode indicar a troca de 10 dezenas por uma centena, ou 10 centenas
por 1 milhar, etc.
Veja um exemplo:
No exemplo que acabamos de ver, o "vai um" indicou a troca de 10 dezenas por
uma centena.
É importante que a criança perceba a relação entre sua ação com o material e os
passos efetuados na operação.

10. O JOGO DE RETIRAR
Objetivos: compreender o mecanismo do "empresta um" nas subtrações com recurso;
estimular o cálculo mental.
Esta atividade pode ser realizada como um jogo de várias rodadas. Em cada rodada, os
grupos sorteiam um cartão e uma papeleta. No cartão há um número e eles devem pegar
as peças correspondentes a essa quantia. Na papeleta há uma ordem que indica quanto
devem tirar da quantidade que têm.
Por exemplo: cartão com número 41 e papeleta com a ordem: TIRE 28.
Vence a rodada o grupo que ficar com as peças que representam o menor número.
Vence o jogo o grupo que ganhar mais rodadas.
É importante que, primeiro, a criança faça várias atividades do tipo: "retire um tanto",
só com o material. Depois que ela dominar o processo de "destroca", pode-se propor
que registre o que acontece no jogo em uma tabela na lousa.
Isto irá proporcionar melhor entendimento do "empresta um" na subtração com recurso.
Quando o professor apresentar essa técnica, poderá concretizar os passos do cálculo
com auxílio do material ou desenhos do material.
O "empresta um" também pode indicar a "destroca" de uma centena por 10 dezenas ou
um milhar por 10 centenas, etc. Veja o jogo seguinte:
11. "DESTROCA"

Objetivos: os mesmos da atividade 10.
Cada grupo de alunos recebe um dado marcado de 4 a 9 e uma placa. Quando o jogador
começa, todos os participantes têm à sua frente uma placa. Cada criança, na sua vez de
jogar, lança o dado e faz as "destrocas" para retirar a quantidade de cubinhos
correspondente ao número que sair no dado. Veja bem: esse número dá direito a retirar
somente cubinhos.
Na quarta rodada, vence quem ficar com as peças que representam o menor número.
Exemplo: Suponha que um aluno tenha tirado 7 no dado. Primeiro ele troca uma placa
por 10 barras e uma barra por 10 cubinhos:
Depois, retira 7 cubinhos:
Salientamos novamente a importância de se proporem várias atividades como essa,
utilizando, de início, só o material. Quando o processo de "destroca" estiver dominado,
pode-se propor que as crianças façam as subtrações envolvidas também com números.
JOGO - BINGO DE BASE DEZ
Estudando o Sistema de Numeração Decimal com a Base Dez, utilizamos o Material
Dourado.
Facilita: A compreensão dos conceitos de unidade, dezena, centena e milhar.
Indicação: 3º, 4º e 5º ano.
Material: Papel quadriculado, lápis de cor, tampinha do jogo de xadrez.
Como jogar: Cada aluno recebe uma cartela contendo a representação decomposta dos
números (quadradinhos). Nestas cartelas eles observam as quantidades de quadrinhos
em cada conjunto, reproduzindo em papel quadriculado e colorindo segundo sua
criatividade.
Marcam utilizando as tampinhas do Jogo de Xadrez.
Com as cartelas e tampinhas organizadas, iniciam o Jogo de Bingo. O professor “canta”
os números e eles marcam nas suas cartelas.

NÚMEROS E SINAIS
Objetivo:Desenvolver e compreender a escrita matemáticas e o uso de sinais.
Organização: Duplas.
Material necessário: Um dado normal, um dado de sinais, um tabuleiro, 20 fichas de
duas cores, sendo 10 de cada cor.
Meta: Alinhar 3 fichas da mesma cor na horizontal, vertical ou diagonal.
Regras do jogo:
 Os jogadores decidem quem começa o jogo.
 Na sua vez, o jogador rola os dois dados e cobre no tabuleiro um número que
corresponde ao que mostra os dados. Exemplo se ele tirou:
1.
Menor
que

Ele cobre um número que seja menor que 3, com uma ficha da sua cor.
 Apenas um número pode ser coberto a cada vez.
 Se não houver casa para colocar a ficha o jogador terá mais uma chance.
 Se jogador cobrir o número errado, ele perde a vez.
 O primeiro jogador que alinhar três de suas fichas na horizontal, vertical ou
diagonal será o vencedor.

JOGO CARTA NA TESTA
Objetivo: Desenvolver a tabuada de multiplicação e compreender a divisão como
operação inversa da multiplicação.
Organização: agrupados em trios, de modo que dois alunos fiquem sentados frente a
frente e o terceiro - o juiz- fique sentado de modo que possa ver os dois.
Material: um baralho com as cartas de ás a 10 de dois naipes, para cada trio, ou 20
cartões numerados dessa forma. No caso de usar baralho, o ás valerá 1.
Desenvolvimento: Os alunos que estão sentados frente a frente recebem, cada um, um
conjunto de cartas de ás a 10, que devem deixar viradas para baixo, na sua frente.
Ambos viram a primeira carta de seu monte e, sem a olhar, colocam-na na testa,
deforma que, tanto seu oponente, quanto o juiz, possam vê-la. O juiz então diz o
resultado da multiplicação dos dois valores. Cada um dos competidores deve tentar
descobrir qual é a carta que tem na testa.Aquele que descobrir primeiro, ganha cinco
pontos. Propor cinco jogadas com essa mesma formação e depois outras tantas com a
mudança da função de cada um, no trio, até que todos tenham desempenhado a função
de juiz. Se o juiz errar a operação perde cinco pontos.
Se for percebida muita disparidade de condições entre os competidores de algum
trio, pode-se optar por alterar os grupos, procurando deixá-los mais ou menos
homogêneos. É interessante realizar novamente esse jogo, estimulando os alunos a
estudar a tabuada em casa, para apresentar melhor desempenho na próxima rodada.

Jogos de Dados - Tabuada
Materiais utilizados: Dois dados. Um contém apenas números ímpares e um curinga e
o outro apenas números pares e um curinga. Esses dados podem ser construídos pelos
próprios alunos e no momento dessa construção pode estar sendo trabalhada com as
crianças a questão das formas geométricas.
Números de jogadores: 2participantes
Regras do jogo:• O primeiro jogador, determinado por sorteio, deve lançar os dois
dados ao mesmo tempo e efetuar a multiplicação dos números indicados.
• Se um dado indicar o número quatro e o outro, o número 5, por exemplo, o jogador
deve multiplicar 4 x 5, se acertar, marca 1 ponto para si e joga uma vez; se errar, não
ganha nenhum ponto, cedendo a vez ao outro jogador.
• Se aparecer o curinga em um dos dados deve-se multiplicar o número do outro dado
por ele mesmo. Se aparecerem dois curingas, o jogador ganha 2 pontos.
OBSERVAÇÕES IMPORTANTES:
Deve-se determinar, com antecedência, o número de jogadores ou a quantidade de
pontos a ser alcançada, vencendo quem obtiver o maior número de pontos ou quem
alcançar primeiro o número de pontos estabelecido.
JOGO DAS FICHAS COLORIDAS
Organização da classe: Formar grupos de 3 a 5 participantes
Capacidades a serem trabalhadas: - Perceber que o número é formado de algarismos
ordenados
- Relacionar as cores das fichas às ordens numéricas

Material: - 10 fichas coloridas (vermelhas, azuis, verdes e brancas) numeradas de 0 a 9
- Cartaz básico (tamanho A4) com cores variadas
Desenvolvimento: Cada jogador pega uma ficha de cada cor e registra o número
formado no quadro somando os valores. Em seguida passa a vez ao colega. Depois da
última jogada ganha aquele que conseguir formar o maior numeral.
Este jogo é utilizado para trabalhar o conceito de ordens e classes, podendo ser
adaptado para o primeiro e segundo ciclo. O mais importante é a interação. Os
participantes podem ajudar um ao outro, mutuamente, sem interferir no desempenho do
vencedor. O professor deve acompanhar o registro do jogo e fazer as explorações
possíveis, graduando as intervenções a cada dia do jogo.
Registro – jogo das fichas coloridas
Aluno(a)
Cartas/Jogadas Vermelha azul Verde branca Número
formado
1ª
2ª
3ª
4ª
5ª

BARALHO DE MULTIPLICAÇÃO
Objetivo:Permitir que o educando exercite e desenvolva o conhecimento relativo a
tabela de multiplicação de forma dinâmica.
Regras:Jogadores: grupos de 2 a 6 pessoas; responsável pelo início do jogo é a pessoa
com mais idade. Antes do início da atividade as cartas devem ser embaralhadas e postas
na mesa. O responsável pelo jogo deve entregar 3 cartas para cada participante;
O primeiro a direita da pessoa que é responsável por iniciar o jogo lança a
primeira carta, após o segundo, terceiro, até o último jogador.
Pega todas as cartas o jogador que tiver jogado a operação cujo resultado da
multiplicação for mais alto. Exemplo de jogo com 3 participantes: Jogador 1 joga 3 x 5=
5- Jogador 2 joga 6 x 7 =42 e jogador 3 lança 2 x 2 = 4, ganha a rodada o jogador 2 e
leva todas as cartas devendo deixá-las de lado para contagem no final da partida.

Após a rodada faz-se nova compra de cartas (3 por participante, sendo
compradas individualmente ou distribuídas pelo responsável pelo jogo, podendo ser
distribuídas cartas de uma em uma ou as três de um só vez, a consenso do grupo), sendo
que as rodadas continuam até o limite das cartas.
Acaba o jogo quando as cartas acabarem, sendo que na última rodada deve-se
observar a quantidade igual de cartas para cada participante, podendo haver sobra de
cartas na mesa, que devem ser descartadas (exemplo de jogo com 3 participantes: na
última rodada sobram 5 cartas sobre a mesa, cada participante deverá pegar 1 carta, as 2
restantes são descartadas do jogo)
Ganha o jogo quem tiver mais cartas ao acabarem as cartas da mesa.
O ganhador é o responsável pelo próximo jogo (embaralhar e distribuir as
cartas).
Cada jogador deve evitar que os adversários percebam quais as cartas que ele
possui na mão.
Material: O baralho pode ser desenvolvido em cartolina com fundo opaco (para evitar a
visualização do conteúdo da carta) e plastificado para maior duração.
Quantidade de cartas do baralho: 90 (9x10) com tabelas do 2 ao 9 que envolvem
atividades de multiplicação da tabela de 1 a 10.
Variações de jogo e/ou baralho: O baralho pode ser desenvolvido com as demais
operações matemáticas (adição, subtração, divisão, etc.);
Ser efetuadas mais cartas para adição ao baralho como: tabela do 0, 1, 10, 11,
etc.).
Para a adição e subtração podem ser confeccionados baralhos com uso de
números, imagens ou ambos. Baralho sem o resultado da operação. Realização do jogo
em duplas (dupla contra dupla).
Sugestão de regras para o Baralho sem resultado da operação: Pode ser realizado
um baralho onde fica disponível somente a operação matemática, sem o resultado da
operação. Para esse baralho devem-se alterar algumas regras do jogo como:

Na hora de jogar, ao ser colocada a carta na mesa: o educando deve dizer o resultado
da operação e caso venha dizer errado a carta automaticamente passa a ser do adversário
que perceber o erro (e estiver na sua vez de jogar), independente de possuir carta maior,
devendo também descartar uma carta da mão e disponibilizar no monte (para a
igualdade de cartas para cada jogador/jogada). Exemplo: jogador 1 joga carta e erra o
resultado, jogador 2 joga e não percebe o erro, jogador 3 percebe o erro do jogador 1,
pega as cartas para si e guarda no seu monte uma das cartas que possuir na mão (carta
essa a sua escolha), seguindo a jogada, caso o jogador que perceber o erro do adversário
seja o penúltimo, ficará também com a carta do último jogador.
Sugestão de regras para o Jogo em duplas: Para o jogo em duplas, os jogadores
devem ficar intercalados, de forma que ao jogar joga um de cada dupla.
Ganha a rodada a dupla que lançar o maior resultado da operação, independente
da jogada do companheiro. Exemplo: Dupla 1: jogador 1 joga 2x2=4; Dupla 2: jogador
1 joga 3x3=9, Dupla 1: Jogador 2 joga 8x9=72, Dupla 2: jogador 2 joga 6x6=36. Ganha
a rodada a dupla um, pois o jogador 2 lançou o maior resultado da operação.
O restante das regras permanecem as mesmas.
MODELO

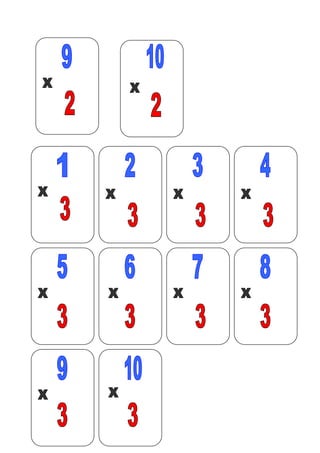
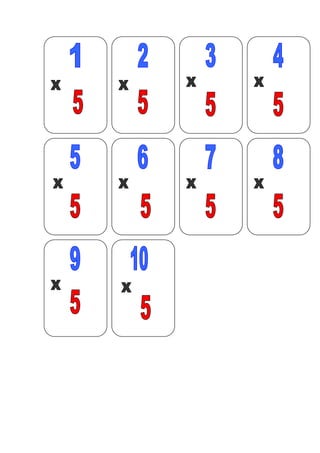
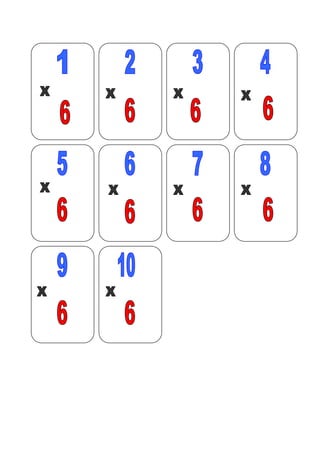
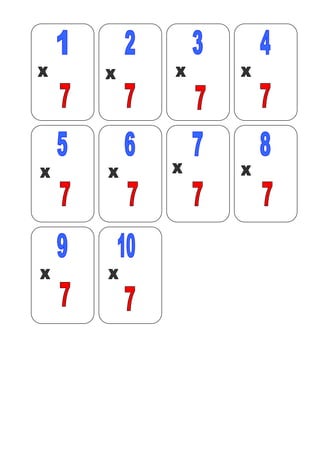
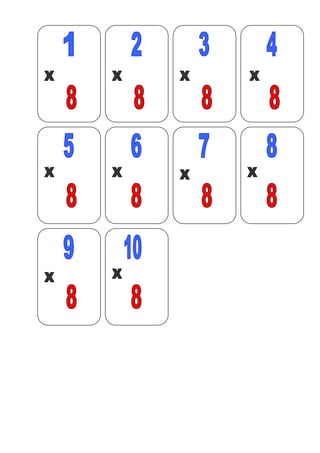
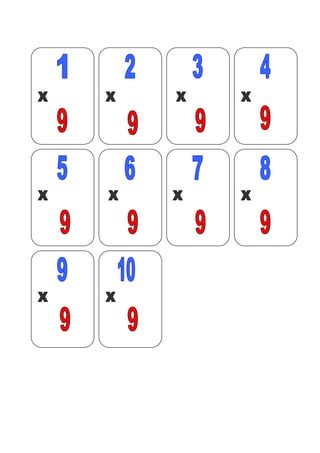
Apostila matematica apoio.2013-05-29_16-23-39

JOGO - Baralho da Tabuada
Objetivos: memorização da tabuada, socialização.
Material: 16 cartas conforme o modelo abaixo.
Número de participantes: 2 a4 pessoas.
Regras: distribua as cartas igualmente, o grupo escolhe a ordem para iniciar o jogo, o
primeiro jogador coloca uma carta na mesa, o próximo deve colocar a carta que tem a
resposta nos cantos, do contrário passa a vez. Vencerá quem primeiro descartar todas as
cartas.

JOGO CONTANDO OS PONTOS
Objetivo: Este jogo auxilia o aluno a desenvolver o cálculo mental, a estimativa e a
compreensão da noção de intervalos na sequência numérica.
Organização da turma: em duplas ou trios.
Material necessário: um quadro de números, uma caixa de pontos para cada grupo e,
fichas para cobrir os números escolhidos.
Meta: conseguir o maior número de pontos ao final de cinco jogadas.
Regras: Após decidir quem começa, os jogadores alternam-se nas jogadas.
1- Proponha aos alunos que observem o quadro com os números que podem ser
usados.
2- Cada jogador, na sua vez, escolhe dois números diferentes do quadro (que
não poderão mais ser escolhidos por outro jogador) e faz a opção por somá-
los ou subtraí-los. Informa seu oponente que operação deseja fazer e diz qual
o resultado da operação, que deve ser feita mentalmente.
3- Se ele estiver correto, verifica em que caixa de pontos está o resultado da
operação feita e marca os pontos obtidos.
4- A cada jogada, os números escolhidos pelos jogadores devem ser
escondidos por fichas ou outro tipo de marcador.

5- Se o jogador efetuar a operação de forma errada, ele perde a vez de jogar.
6- Depois de cinco jogadas para cada jogador, ganha o que tiver o maior total
de pontos.
Quadro de números para o jogo contando pontos
15 80 120 560 700
345 75 140 125 780
40 130 10 70 550
400 65 90 300 450 85 70
5 780 900 25 55 105 60
35 85 870 505 960
Caixa de pontos para o resultado R
1 ponto 5 pontos 10 pontos 5 pontos 1 ponto
R menor que R entre R entre R entre R maior
100 101 e 200 201 e 300 301 e 400 que 401
JOGO DE CÁLCULO MENTAL
Objetivo: Desenvolver o raciocínio, através de cálculo mental, estratégia e fixação das
operações básicas.
Indicação: 4º e 5º Anos.
Material: Tabuleiro (figura 2), 25 fichas de uma cor, 25 fichas de outra cor e 3 dados.

0 1 2 3 4 5 6 7
27 28 29 30 31 32 33 8
26 54 55 60 64 66 34 9
25 50 120 125 144 72 35 10
24 48 108 180 150 75 36 11
23 45 100 96 90 80 37 12
22 44 42 41 40 39 38 13
21 20 19 18 17 16 15 14
Como jogar: Os adversários jogam alternadamente. Cada jogador joga os três dados ao
mesmo tempo e constrói uma sentença numérica usando os números indicados e uma ou
duas operações diferentes. Por exemplo, com os números 2, 3 e 4, o jogador poderá
construir (2+3) x 4 =20. O jogador, neste caso, cobriria o espaço marcado 20 com uma
ficha de sua cor. Só é permitido utilizar as quatro operações básicas.
A contagem de pontos: Um ponto é obtido por colocar uma ficha num espaço
desocupado que seja adjacente a um espaço com uma ficha já colocada
(horizontalmente, verticalmente ou diagonalmente). Colocando-se uma ficha num
espaço adjacente a mais de 1 espaço ocupado, mais pontos poderão ser obtidos. Por
exemplo, se os espaços 0, 1 e 27 estiverem ocupados (ver o tabuleiro), o jogador
ganharia 3 pontos colocando uma ficha no espaço 28. A cor das fichas nos espaços
ocupados não faz diferença. Os pontos obtidos numa jogada são somados para o
jogador.
Se um jogador passar sua jogada, por achar que não é possível fazer uma
sentença com aqueles valores dos dados para ocupar um espaço no tabuleiro vazio, o
adversário terá uma opção a tomar: se ele achar que seria possível fazer uma sentença
com os dados jogados pelo colega, ele poderá fazê-la, antes de iniciar sua própria
jogada. Ele ganhará, nesse caso, o dobro do número de pontos, e em seguida poderá
fazer sua própria jogada.
O jogo termina quando o jogador conseguir atingir o número de pontos definidos
no início do jogo (30, 40 ou 60) ou ao colocar 5 fichas de mesma cor em linha reta sem
nenhuma ficha do adversário intervindo. Essa linha poderá ser horizontal, vertical ou
diagonal.

CORRIDA AO DEZ
Facilita: Memorização de operações algébricas e raciocínio.
Material: Papel, régua e lápis
Como jogar: Dois jogadores deverão pegar uma folha qualquer e desenhar uma
pequena tabela com duas colunas, e no início de cada coluna deverão colocar os seus
respectivos nomes.
Feito isso, deverão decidir quem será o primeiro a iniciar, pode ser por par-ou-ímpar ou
por outra forma.
O primeiro jogador escreve o número 1 ou 2 do seu lado da tabela. O segundo deve
pegar o número anterior, somar mentalmente 1 ou 2 a ele e escrever o resultado na sua
parte da tabela, e assim segue, sempre somando 1 ou 2 ao anterior e escrevendo em sua
coluna até a soma chegar ao dez.
Ganha aquele que conseguir escrever o número dez primeiro.
Exemplo:
Veja: o primeiro a jogar escreve em sua coluna o número 1 ou o 2. O outro jogador
soma, mentalmente, 1 ou 2 ao número escrito e escreve em sua coluna, na próxima
linha, a soma obtida. Como na figura abaixo:
Pedro Luiz
2 3
5 7
8 10

REFERÊNCIAS
http://espacoeducar-liza.blogspot.com.br/2009/03/domino-fracionario.html
http://www.uesb.br/mat/semat/seemat_arquivos/docs/o5.pdf
http://rachacuca.com.br/enigmas/raciocionio-logico/
http://profcrika.blogspot.com.br/2010/08/serpentes-e-escadas-organizacao-da.html
http://rachacuca.com.br/logica/problemas/presentes-de-natal/
DANTE,Luiz Roberto. Didática da resolução de problemas. 12º.ed.SãoPaulo:Ática, 2007.
IMENES ,L.M. eLELLIS M..Matemática paratodos .3º.ed.SãoPaulo, 2007.
SMOLE, K.C.S. e DINIZ, M.I.Cadernos do mathema. 1º.ed.:SãoPaulo: Artmed, 2007.
SADOVSKY, Patrícia. O ensino da matemática hoje. 1º.ed:SãoPaulo: Ática, 2007.
GIOVANNI, J.J.R.e CASTRUCCI, B. Aconquista da matemática. 1º.ed:SãoPaulo: FTD, 2009.
ProfessoraAdriana Fernandes Bambinetti
E-mail: adrika.fernandes@gmail.com

Apostila matematica apoio.2013-05-29_16-23-39

Mais conteúdo relacionado

Mais procurados (17)

Destaque (20)

Semelhante a Apostila matematica apoio.2013-05-29_16-23-39 (20)

Último (20)

Apostila matematica apoio.2013-05-29_16-23-39