ESFUERZOS EN RECIPIENTES DE PAREDES DELGADAS (TUBULARES)
- 1. ESCUELA PROFESIONAL DE INGENIERÍA CIVIL CURSO : MECÁNICA DE SOLIDOS DOCENTE : ING. LUIS SILVA TEMAS : - ESFUERZOS EN RECIPIENTES DE PAREDES DELGADAS (TUBULARES) - DEFORMACIÓN EN VIGAS (CURVA ELÁSTICA) - FLEXIÓN ALUMNO : RAFAEL LIVAQUE, Néstor CICLO : IV CHOTA – PERÚ 2015
- 2. ESCUELA PROFESIONAL DE INGENIERÍA CIVIL Mecánica de Solidos 1 INTRODUCCIÓN Se deducen las ecuaciones para calcular los esfuerzos en las paredes de los cilindros de pared delgada, tales como: los domos de las calderas, las tuberías, los separadores de fluidos en la industria petrolera, los tanques llamados "salchichas" y los tanque esféricos llamados "esferas" en la industria petrolera. Se detalla las deformaciones de vigas donde se estudiará en especial la curva elástica. También se hablará de flexión en vigas. La utilidad de estos conocimientos está en el diseño de los dispositivos mecánicos señalados, y en la impartición de las materias de la carrera Ingeniero Civil.
- 3. ESCUELA PROFESIONAL DE INGENIERÍA CIVIL Mecánica de Solidos 2 I. MARCO TEÓRICO 1.1. RECIPIENTES DE PAREDES DELGADAS (TUBULARES) Los recipientes de pared delgada constituyen una aplicación importante del análisis de esfuerzo plano. Como sus paredes oponen poca resistencia a la flexión, puede suponerse que las fuerzas internas ejercidas sobre una parte de la pared son tangentes a la superficie del recipiente. Considerando recipiente cilíndrico de radio interior r y espesor de pared t, que contiene un fluido a presión Se van a determinar los esfuerzos ejercidos sobre un pequeño elemento de pared con lados respectivamente paralelos y perpendiculares al eje del cilindro. Debido a la simetría axial del recipiente y de su contenido, no se ejercen esfuerzos cortantes sobre el elemento. A. DIFERENCIA ENTRE CILINDROS DE PARED GRUESA Y CILINDROS DE PARED DELGADA Un cilindro es de pared delgada cuando hay una gran diferencia entre el espesor de la pared y el diámetro del mismo, en un cilindro de pared gruesa no sucede lo mismo. r t
- 4. ESCUELA PROFESIONAL DE INGENIERÍA CIVIL Mecánica de Solidos 3 Por otro lado, la distribución de esfuerzo en el espesor de las paredes del cilindro de pared delgada es uniforme, mientras que en el cilindro de pared gruesa no sucede así. Los cilindros de pared gruesa son los que constituyen los barriles o cañones de las armas de fuego. En nuestro caso, veremos el diseño de un cilindro de pared delgada. B. ESFUER ZO EN RECIPIENTES DE PARED FINA. El supuesto de pared delgada para ser válido en un recipiente esta debe tener un espesor de pared de no más de aproximadamente una décima parte (a menudo citada como un veinteavo) de su radio. Esto permite que para el tratamiento de la pared como una superficie, y posteriormente usando la ecuación de Laplace-Young estimar de la tensión circunferencial creado por una presión interna en un recipiente a presión cilíndrico de pared delgada: (Para un cilindro) (Para una esfera) Donde: P = es la presión interna
- 5. ESCUELA PROFESIONAL DE INGENIERÍA CIVIL Mecánica de Solidos 4 e = es el espesor de la pared r = es el radio interior del cilindro. = es la tensión circunferencial. Cuando el recipiente se ha cerrado termina actúa la presión interna sobre ellos para desarrollar una fuerza a lo largo del eje del cilindro. Esto se conoce como la tensión axial y es usualmente menor que la tensión circunferencial. Aunque esto puede ser aproximado a Que resulta ser aproximadamente la mitad de la tangencial. 1.2. DEFORMACIÓN EN VIGAS La viga suele dividirse en vigas isostáticas e hiperestáticas. Recordemos que esta división corresponde a las condiciones de apoyo que presente el elemento a analizar Si la viga tiene un número igual o inferior a tres incógnitas en sus reacciones, bastará con aplicar las condiciones de equilibrio estático para resolverla. ΣFx = 0, ΣFy = 0, ΣM = 0 Si en cambio, la viga presenta un mayor número de incógnitas, no bastará con las ecuaciones antes indicadas, sino que será necesario incorporar nuevas
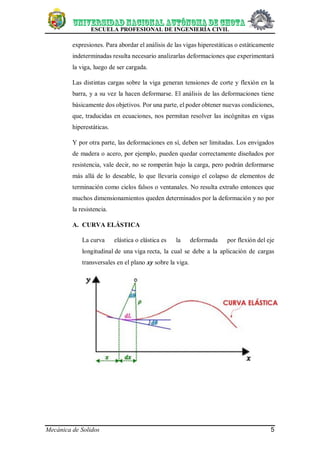
- 6. ESCUELA PROFESIONAL DE INGENIERÍA CIVIL Mecánica de Solidos 5 expresiones. Para abordar el análisis de las vigas hiperestáticas o estáticamente indeterminadas resulta necesario analizarlas deformaciones que experimentará la viga, luego de ser cargada. Las distintas cargas sobre la viga generan tensiones de corte y flexión en la barra, y a su vez la hacen deformarse. El análisis de las deformaciones tiene básicamente dos objetivos. Por una parte, el poder obtener nuevas condiciones, que, traducidas en ecuaciones, nos permitan resolver las incógnitas en vigas hiperestáticas. Y por otra parte, las deformaciones en sí, deben ser limitadas. Los envigados de madera o acero, por ejemplo, pueden quedar correctamente diseñados por resistencia, vale decir, no se romperán bajo la carga, pero podrán deformarse más allá de lo deseable, lo que llevaría consigo el colapso de elementos de terminación como cielos falsos o ventanales. No resulta extraño entonces que muchos dimensionamientos queden determinados por la deformación y no por la resistencia. A. CURVA ELÁSTICA La curva elástica o elástica es la deformada por flexión del eje longitudinal de una viga recta, la cual se debe a la aplicación de cargas transversales en el plano xy sobre la viga.
- 7. ESCUELA PROFESIONAL DE INGENIERÍA CIVIL Mecánica de Solidos 6
- 8. ESCUELA PROFESIONAL DE INGENIERÍA CIVIL Mecánica de Solidos 7 3.1. FLEXIÓN. En ingeniería se denomina flexión al tipo de deformación que presenta un elemento estructural alargado en una dirección perpendicular a su eje longitudinal. El término "alargado" se aplica cuando una dimensión es dominante frente a las otras. Un caso típico son las vigas, las que están diseñadas para trabajar, principalmente, por flexión. Igualmente, el concepto de flexión se extiende a elementos estructurales superficiales como placas o láminas. El rasgo más destacado es que un objeto sometido a flexión presenta una superficie de puntos llamada fibra neutra tal que la distancia a lo largo de cualquier curva contenida en ella no varía con respecto al valor antes de la deformación. El esfuerzo que provoca la flexión se denomina momento flector.
- 9. ESCUELA PROFESIONAL DE INGENIERÍA CIVIL Mecánica de Solidos 8 A. FLEXIÓN EN VIGAS Y ARCOS Las vigas o arcos son elementos estructurales pensados para trabajar predominantemente en flexión. Geométricamente son prismas mecánicos cuya rigidez depende, entre otras cosas, del momento de inercia de la sección transversal de las vigas. Existen dos hipótesis cinemáticas comunes para representar la flexión de vigas y arcos: La hipótesis de Navier-Euler-Bernouilli. En ella las secciones transversales al eje baricéntrico se consideran en primera aproximación indeformables y se mantienen perpendiculares al mismo (que se curva) tras la deformación. La hipótesis de Timoshenko. En esta hipótesis se admite que las secciones transversales perpendiculares al eje baricéntrico pasen a formar un ángulo con ese eje baricéntrico por efecto del esfuerzo cortante. B. TEORÍA DE EULER-BERNOULLI La teoría de Euler-Bernoulli para el cálculo de vigas es la que se deriva de la hipótesis cinemática de Euler-Bernouilli, y puede emplearse para calcular tensiones y desplazamientos sobre una viga o arco de longitud de eje grande comparada con el canto máximo o altura de la sección transversal. Para escribir las fórmulas de la teoría de Euler-Bernouilli conviene tomar un sistema de coordenadas adecuado para describir la geometría, una viga es de hecho un prisma mecánico sobre el que se pueden considerar las coordenadas (s, y, z) con s la distancia a lo largo del eje de la viga e (y, z) las coordenadas sobre la sección transversal. Para el caso de arcos este sistema de coordenas es curvilíneo, aunque para vigas de eje recto puede tomarse como cartesiano (y en ese caso s se nombra como x). Para una viga de sección recta la tensión el caso de flexión compuesta esviada la tensión viene dada por la fórmula de Navier:
- 10. ESCUELA PROFESIONAL DE INGENIERÍA CIVIL Mecánica de Solidos 9 Donde: son los segundos momentos de área (momentos de inercia) según los ejes Y y Z. es el momento de área mixto o producto de inercia según los ejes Z e Y. son los momentos flectores según las direcciones Y y Z, que en general varíarán según la coordenada x. es el esfuerzo axial a lo largo del eje. Si la dirección de los ejes de coordenadas (y, z) se toman coincidentes con las direcciones principales de inercia entonces los productos de inercia se anulan y la ecuación anterior se simplifica notablemente. Además si se considera el caso de flexión simple no-desviada las tensiones según el eje son simplemente: Por otro lado, en este mismo caso de flexión simple no esviada, el campo de desplazamientos, en la hipótesis de Bernoulli, viene dada por la ecuación de la curva elástica: Donde: representa la flecha, o desplazamiento vertical, respecto de la posición inicial sin cargas. representa el momento flector a lo largo de la ordenada x. el segundo momento de inercia de la sección transversal. el módulo de elasticidad del material. representa las cargas a lo largo del eje de la viga.
- 11. ESCUELA PROFESIONAL DE INGENIERÍA CIVIL Mecánica de Solidos 10 C. TEORÍA DE TIMOSHENKO Esquema de deformación de una viga que ilustra la diferencia entre la teoría de Timoshenko y la teoría de Euler- Bernouilli: en la primera θi y dw/dxi no tienen necesariamente que coincidir, mientras que en la segunda son iguales. La diferencia fundamental entre la teoría de Euler-Bernouilli y la teoría de Timoshenko es que en la primera el giro relativo de la sección se aproxima mediante la derivada del desplazamiento vertical, esto constituye una aproximación válida sólo para piezas largas en relación a las dimensiones de la sección transversal, y entonces sucede que las deformaciones debidas al esfuerzo cortante son despreciables frente a las deformaciones ocasionadas por el momento flector. En la teoría de Timoshenko, donde no se desprecian las deformaciones debidas al cortante y por tanto es válida también para vigas cortas, la ecuación de la curva elástica viene dada por el sistema de ecuaciones más complejo: Derivando la primera de las dos ecuaciones anteriores y substituyendo en ella la segunda llegamos a la ecuación de la curva elástica incluyendo el efecto del esfuerzo cortante:
- 12. ESCUELA PROFESIONAL DE INGENIERÍA CIVIL Mecánica de Solidos 11 BIBLIOGRAFÍA Fitzgerald, Robert W. Resistencia de materiales. Fondo Educativo Interamericano, S. A. y Representaciones y Servicios de Ingeniería, México, 1970 Sloane, Alvin. Mechanics of materials, The MacMillanCo.EEUU,1960 Balanzá, Julio C. Resistencia de materiales teoría y práctica. Universidad Veracruzana, Xalapa Ver., México, 1993. Timoshenko, Stephen; Godier J.N. (1951). McGraw-Hill, ed. Theory of elasticity. Ortiz Berrocal, Luis (1991). McGraw-Hill, ed. Resistencia de Materiales. Aravaca (Madrid). ISBN 84-7651-512-3. Monleón Cremades, S., Análisis de vigas, arcos, placas y láminas, Ed. UPV, 1999, ISBN 84-7721-769-6.
- 13. ESCUELA PROFESIONAL DE INGENIERÍA CIVIL Mecánica de Solidos 12 ANEXOS EJEMPLOS DE RECIPIENTES DE PAREDES DELGADAS (TUBULARES) EJEMPLO 1 El cilindro mostrado en la figura, esta sujeto a una presión interna de 400psi ( pounds per square inch) (lb /pulg2). El diámetro del cilindro es de 30 pulgadas y el espesor de la pared es media pulgada. ¿Cuál es el esfuerzo de tensión más grande en el espesor de las paredes? RESPUESTA El esfuerzo de tensión más grande será el ST1 de acuerdo a lo que acabamos de ver Datos: P = 400psi r = 15 pulg. t = 0.5 pulg. Incógnita ST1= ¿ Ecuación: ST1= t pr Sustituyendo valores tenemos: ST1= 5.0 )15(400 ST1= 12 000 psi
- 14. ESCUELA PROFESIONAL DE INGENIERÍA CIVIL Mecánica de Solidos 13 EJEMPLOS DE DEFORMACIÓN EN VIGAS – CURVA ELÁSTICA Ejemplo 01
- 15. ESCUELA PROFESIONAL DE INGENIERÍA CIVIL Mecánica de Solidos 14
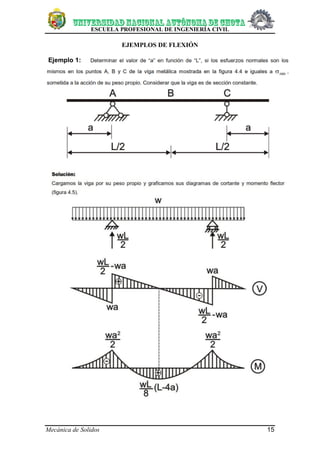
- 16. ESCUELA PROFESIONAL DE INGENIERÍA CIVIL Mecánica de Solidos 15 EJEMPLOS DE FLEXIÓN Ejemplo 1:
- 17. ESCUELA PROFESIONAL DE INGENIERÍA CIVIL Mecánica de Solidos 16