Cap iii equilibrio de un sistema de fuerzas
- 2. Un Sistema de fuerzas en un plano (coplanares) se encuentra en equilibrio cuando su Resultante es nula, es decir cuando su resultante no es un par ni una fuerza.
- 3. Por esta razón se acostumbra decir que un Sistema de fuerzas en equilibrio es aquel en el que NO tiene resultante.
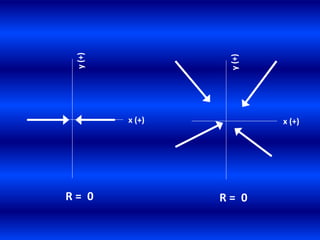
- 4. y(+) R = 0 x (+) y(+) R = 0 x (+)
- 5. Son aquellas ecuaciones que da la Estática y que deben ser verificadas por todo sistema de fuerzas en equilibrio y se expresan como:
- 6. + n i = 1 Σ Fix = 0 + n i = 1 Σ Fiy = 0 + n i = 1 Σ Mi = 0
- 7. En seguida veremos diferentes tipos de apoyos en los cuales se sustentan las estructuras, los objetos, etc.
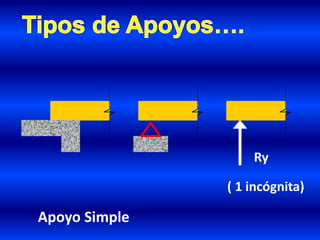
- 8. a).- Apoyo Simple: Únicamente impide el movimiento vertical, pero no el deslizamiento horizontal, se representa como:
- 9. ( 1 incógnita) Ry Apoyo Simple
- 10. Ruinas de Stonehenge Inglaterra Ejemplo de Apoyo Simple
- 11. Ejemplo de Apoyo Simple
- 12. Ejemplo de Apoyo Simple
- 13. b).- Apoyo Desplazable: La reacción es normal a la superficie. ( 1 incógnita) Ry
- 14. Ejemplo de Apoyo Desplazable
- 15. Ejemplo de Apoyo Desplazable
- 16. Ejemplo de Apoyo Desplazable
- 17. Ejemplo de Apoyo Desplazable
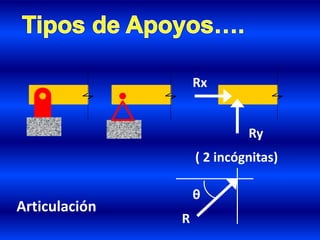
- 18. c).- Articulación: No se permite la traslación en ninguna dirección (o sea impide el movimiento en el eje “x” ó en el eje “y”) pero no puede impedir la rotación. La Resultante tiene dirección desconocida.
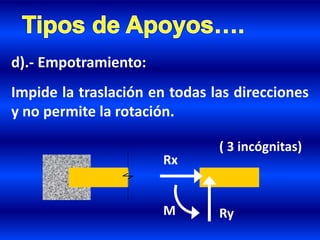
- 23. d).- Empotramiento: Impide la traslación en todas las direcciones y no permite la rotación. ( 3 incógnitas) Ry Rx M
- 25. ( 1 incógnita) Rx e).- Apoyo Guiado La reacción es normal a la superficie de rodamiento.
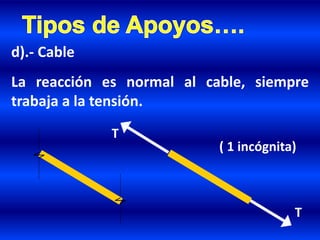
- 26. ( 1 incógnita) T d).- Cable La reacción es normal al cable, siempre trabaja a la tensión. T
- 27. ( 1 valor) Wpp e).- Peso propio Siempre señala a la superficie de la tierra en forma vertical por efectos de la gravedad c.g. Tierra Por último: Aunque no es Apoyo es un valor muy común en los problemas de equilibrio estático.
- 28. Según el número de incógnitas que presenten los problemas de equilibrio, éstos pueden clasificarse en: a).- Isostáticos b).- Hiperestáticos c).- Hipostáticos
- 29. Problemas Isostáticos: También llamados estáticamente determi- nados, son aquellos en que el número de incógnitas que presenta NO es mayor que el número de ecuaciones de equilibrio con que se cuenta para resolverlos
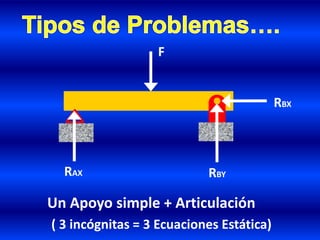
- 30. Un Apoyo simple + Articulación ( 3 incógnitas = 3 Ecuaciones Estática) RBX RBYRAX F
- 31. Problemas Hiperestáticos: También llamados estáticamente indeter- minados, son aquellos en que el número de incógnitas que presenta ES mayor que el número de ecuaciones de equilibrio con que se cuenta para resolverlos
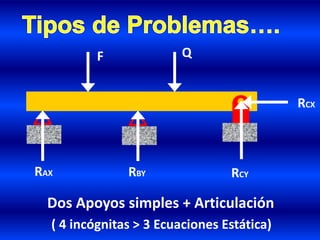
- 32. Dos Apoyos simples + Articulación ( 4 incógnitas > 3 Ecuaciones Estática) RCX RBYRAX F Q RCY
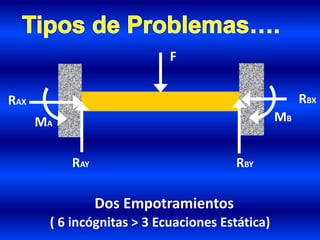
- 33. Dos Empotramientos ( 6 incógnitas > 3 Ecuaciones Estática) RBX RAY RAX F RBY MA MB
- 34. Según sea el número de incógnitas mayor que el de las ecuaciones de equilibrio estático, se dice que es el grado de Hiperestaticidad del problema. Para el ejemplo anterior: 6 incógnitas – 3 ecuaciones de equilibrio Igual a 3er grado de hiperestaticidad
- 35. Problemas Hipostáticos: También llamados inestables, en este caso el número de incógnitas que presenta ES superado por el número de ecuaciones de equilibrio con que se cuenta para resolverlos
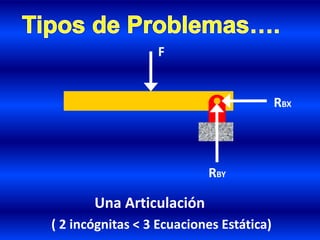
- 36. Una Articulación ( 2 incógnitas < 3 Ecuaciones Estática) RBX RBY F
- 37. n i = 1 Un sistema de “n” Fuerzas Colineales estará en equilibrio cuando tiene una Resultante igual a cero. Alguna incógnita se obtiene por una simple suma algebraica, igual a cero. Σ Fi = 0
- 38. Por ejemplo F1= 100 Kg Determinar la Fuerza que debe ejercer el ultimo hombre de la derecha, para que el banderín central no se mueva, si cada hombre sujeta la cuerda con las siguientes fuerzas: F3= 100 KgF2= 75 KgF1= 80 Kg F4= 90 Kg F5= 95 Kg F6= ?
- 39. + n i = 1 Σ Fi = 0 0 = - 80 – 75 – 100 + 90 + 95 + F6 F6 = 70 Kg F3= 100 KgF2= 75 KgF1= 80 Kg F4= 90 Kg F5= 95 Kg F6= ? 0 = F1 + F2 + F3 + F4 + F5 + F6 Resp
- 41. En este tipo de problemas, solo se pueden tener como máximo dos incógnitas ya que solo habrá dos ecuaciones de equilibrio estático disponibles: + n i = 1 Σ Fix = 0 + n i = 1 Σ Fiy = 0
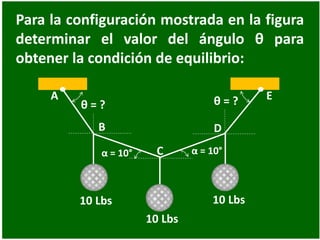
- 42. 10 Lbs Para la configuración mostrada en la figura determinar el valor del ángulo θ para obtener la condición de equilibrio: α = 10° θ = ? 10 Lbs 10 Lbs α = 10° θ = ?A B C D E
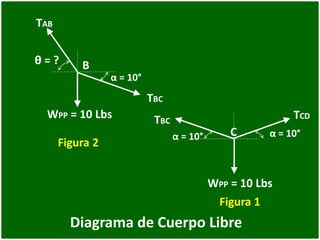
- 43. WPP = 10 Lbs Diagrama de Cuerpo Libre α = 10° θ = ? α = 10° TAB B C TBC TBC α = 10° TCD WPP = 10 Lbs Figura 2 Figura 1
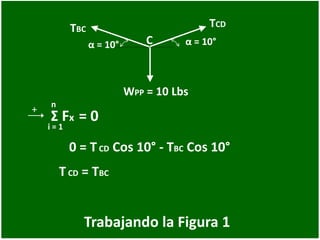
- 44. Trabajando la Figura 1 α = 10°C TBC α = 10° TCD WPP = 10 Lbs 0 = TCD Cos 10° - TBC Cos 10° + n i = 1 Σ Fx = 0 TCD = TBC
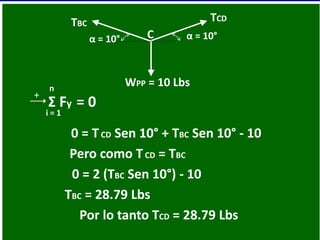
- 45. α = 10°C TBC α = 10° TCD WPP = 10 Lbs 0 = TCD Sen 10° + TBC Sen 10° - 10 + n i = 1 Σ Fy = 0 Pero como TCD = TBC 0 = 2 (TBC Sen 10°) - 10 TBC = 28.79 Lbs Por lo tanto TCD = 28.79 Lbs
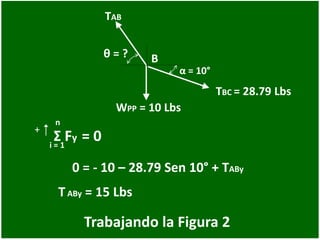
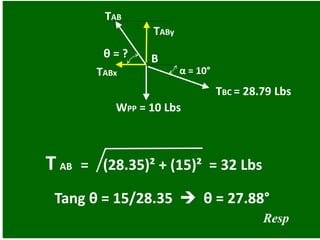
- 46. Trabajando la Figura 2 0 = - 10 – 28.79 Sen 10° + TABy + n i = 1 Σ Fy = 0 TABy = 15 Lbs WPP = 10 Lbs α = 10° θ = ? TAB B TBC = 28.79 Lbs
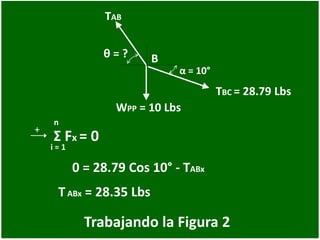
- 47. Trabajando la Figura 2 0 = 28.79 Cos 10° - TABx + n i = 1 Σ Fx = 0 TABx = 28.35 Lbs WPP = 10 Lbs α = 10° θ = ? TAB B TBC = 28.79 Lbs
- 48. WPP = 10 Lbs α = 10° θ = ? TAB B TBC = 28.79 Lbs TABy T AB = (28.35)² + (15)² = 32 Lbs Tang θ = 15/28.35 θ = 27.88° TABx Resp
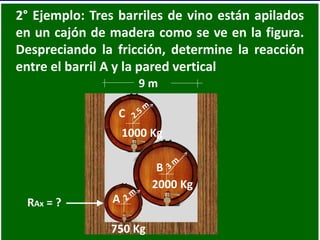
- 49. 2° Ejemplo: Tres barriles de vino están apilados en un cajón de madera como se ve en la figura. Despreciando la fricción, determine la reacción entre el barril A y la pared vertical 9 m 10 Lbs A B C 1000 Kg 2000 Kg 750 Kg RAx = ?
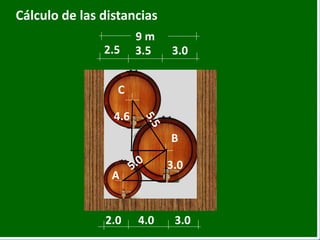
- 50. Cálculo de las distancias 9 m 10 Lbs A B C 2.5 3.03.5 2.0 3.04.0 3.0 4.6
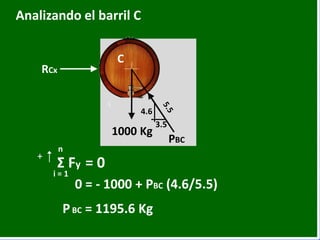
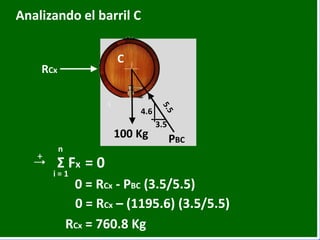
- 51. Kg Analizando el barril C RCx PBC C 3.5 1000 Kg 4.6 0 = - 1000 + PBC (4.6/5.5) + n i = 1 Σ Fy = 0 PBC = 1195.6 Kg
- 52. Kg Analizando el barril C RCx PBC C 3.5 100 Kg 4.6 0 = RCx - PBC (3.5/5.5) + n i = 1 Σ Fx = 0 RCx = 760.8 Kg 0 = RCx – (1195.6) (3.5/5.5)
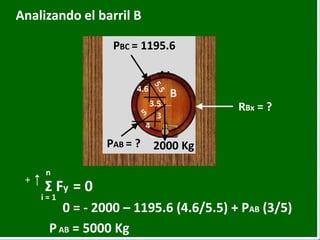
- 53. Analizando el barril B 10 Lbs B 3.5 4 3 4.6 PBC = 1195.6 2000 KgPAB = ? RBx = ? 0 = - 2000 – 1195.6 (4.6/5.5) + PAB (3/5) + n i = 1 Σ Fy = 0 PAB = 5000 Kg
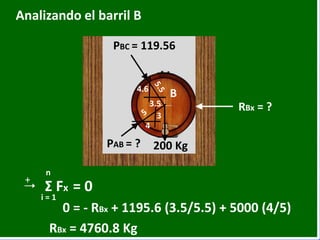
- 54. Analizando el barril B 10 Lbs B 3.5 4 3 4.6 PBC = 119.56 200 KgPAB = ? RBx = ? 0 = - RBx + 1195.6 (3.5/5.5) + 5000 (4/5) + n i = 1 Σ Fx = 0 RBx = 4760.8 Kg
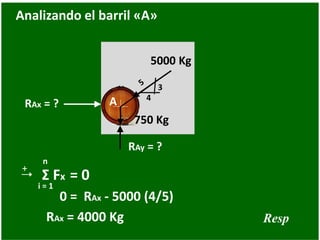
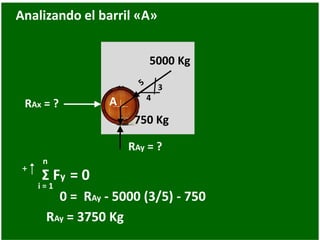
- 55. i Analizando el barril «A» A 4 3 RAx = ? 750 Kg 5000 Kg 0 = RAx - 5000 (4/5) + n i = 1 Σ Fx = 0 RAx = 4000 Kg RAy = ? Resp
- 56. i Analizando el barril «A» A 4 3 RAx = ? 750 Kg 5000 Kg 0 = RAy - 5000 (3/5) - 750 + n i = 1 Σ Fy = 0 RAy = 3750 Kg RAy = ?
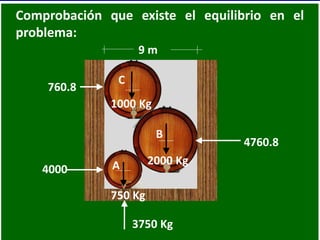
- 57. Comprobación que existe el equilibrio en el problema: 9 m 10 Lbs A B C 1000 Kg 2000 Kg 750 Kg 4000 3750 Kg 760.8 4760.8
- 59. En este tipo de problemas, solo se pueden tener como máximo dos incógnitas ya que solo habrá dos ecuaciones de equilibrio estático disponibles: + n i = 1 Σ Fix = 0 + n i = 1 Σ Fiy = 0 Fuerzas en sentido x Fuerzas en sentido y Σ M = Σ Fix diy = 0+ i = 1 n Σ M = Σ Fiy dix = 0+ i = 1 n
- 60. La grúa esquematizada en la figura pesa 25 Ton y su centro de gravedad G esta a 2 m, del eje delantero, dada las dimensiones, encontrar el valor de la carga máxima W que puede levantar, asumiendo que la carga permisible en el eje B es de 30 Ton. 6 m 2 m
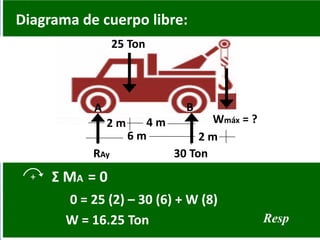
- 61. Diagrama de cuerpo libre: 6 m 2 m 2 m 4 m 25 Ton 30 TonRAy Wmáx = ? A B 0 = 25 (2) – 30 (6) + W (8) + Σ MA = 0 W = 16.25 Ton Resp
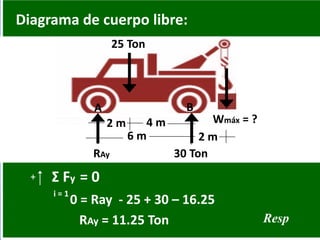
- 62. Diagrama de cuerpo libre: 6 m 2 m 2 m 4 m 25 Ton 30 TonRAy Wmáx = ? A B 0 = Ray - 25 + 30 – 16.25 + Σ Fy = 0 RAy = 11.25 Ton Resp i = 1
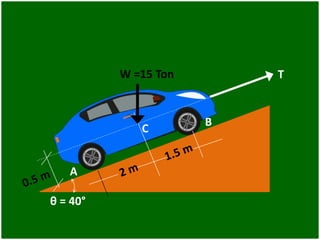
- 63. 2° Problema: Un carro está estacionado sobre el plano inclinado mostrado en la figura. El peso del carro está representado por la fuerza de 15 Ton que pasa por el punto C.- Determinar: a) La Tensión en el cable, necesaria para sostener el carro b) ¿Cuál será la reacción en las ruedas?
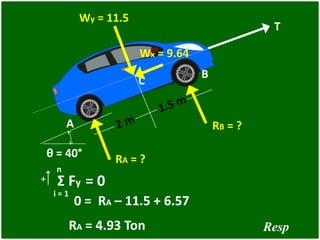
- 64. θ = 40° A B W =15 Ton C T
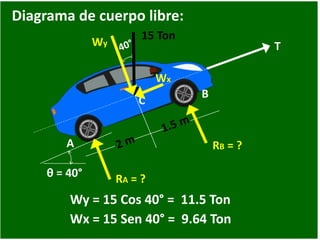
- 65. θ = 40° A B 15 Ton C T Wy = 15 Cos 40° = 11.5 Ton RA = ? RB = ? Wx = 15 Sen 40° = 9.64 Ton Wy Wx Diagrama de cuerpo libre:
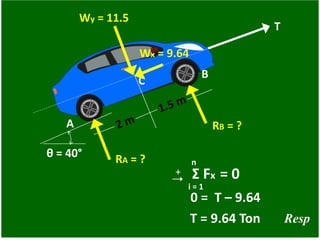
- 66. θ = 40° A B C T RA = ? RB = ? Wy = 11.5 Wx = 9.64 + n i = 1 Σ Fx = 0 T = 9.64 Ton 0 = T – 9.64 Resp
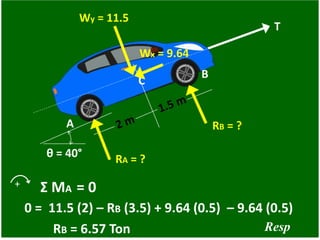
- 67. θ = 40° A B C T RA = ? RB = ? Wy = 11.5 Wx = 9.64 + Σ MA = 0 RB = 6.57 Ton 0 = 11.5 (2) – RB (3.5) + 9.64 (0.5) – 9.64 (0.5) Resp
- 68. θ = 40° A B C T RA = ? RB = ? Wy = 11.5 Wx = 9.64 + n i = 1 Σ Fy = 0 RA = 4.93 Ton 0 = RA – 11.5 + 6.57 Resp
- 70. En este tipo de problemas, solo se pueden tener como máximo tres incógnitas ya que solo habrá tres ecuaciones de equilibrio estático disponibles: + n i = 1 Σ Fix = 0 + n i = 1 Σ Fiy = 0 + n i = 1 Σ Mi = 0
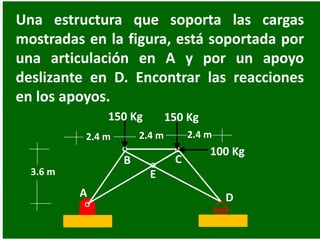
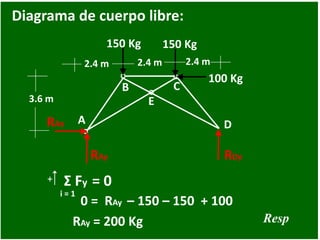
- 71. Una estructura que soporta las cargas mostradas en la figura, está soportada por una articulación en A y por un apoyo deslizante en D. Encontrar las reacciones en los apoyos. 2.4 m 150 Kg A B C D E 2.4 m 3.6 m 2.4 m 150 Kg 100 Kg
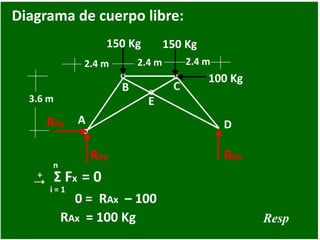
- 72. 2.4 m 150 Kg A B C D E 2.4 m 3.6 m 2.4 m 150 Kg 100 Kg Diagrama de cuerpo libre: RAy RDy RAx + n i = 1 Σ Fx = 0 0 = RAx – 100 RAx = 100 Kg Resp
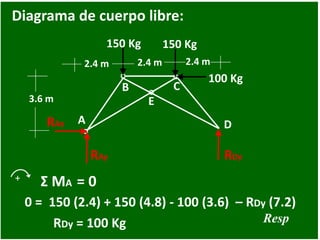
- 73. 2.4 m 150 Kg A B C D E 2.4 m 3.6 m 2.4 m 150 Kg 100 Kg Diagrama de cuerpo libre: RAy RDy RAx + Σ MA = 0 RDy = 100 Kg 0 = 150 (2.4) + 150 (4.8) - 100 (3.6) – RDy (7.2) Resp
- 74. 2.4 m 150 Kg A B C D E 2.4 m 3.6 m 2.4 m 150 Kg 100 Kg Diagrama de cuerpo libre: RAy RDy RAx + i = 1 Σ Fy = 0 RAy = 200 Kg 0 = RAy – 150 – 150 + 100 Resp
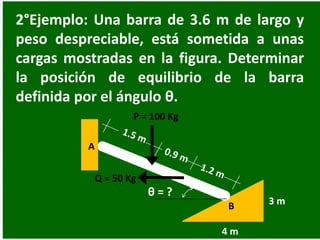
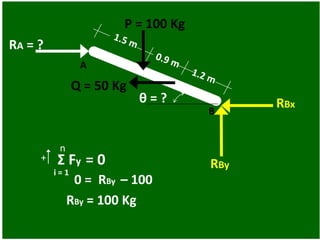
- 75. 2°Ejemplo: Una barra de 3.6 m de largo y peso despreciable, está sometida a unas cargas mostradas en la figura. Determinar la posición de equilibrio de la barra definida por el ángulo θ. 4 m 3 m θ = ? P = 100 Kg Q = 50 Kg A B
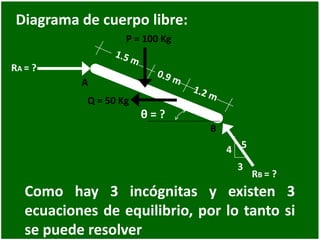
- 76. Diagrama de cuerpo libre: 4 3 θ = ? P = 100 Kg Q = 50 Kg A B RA = ? 5 RB = ? Como hay 3 incógnitas y existen 3 ecuaciones de equilibrio, por lo tanto si se puede resolver
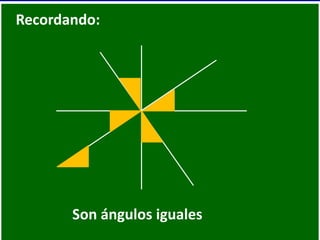
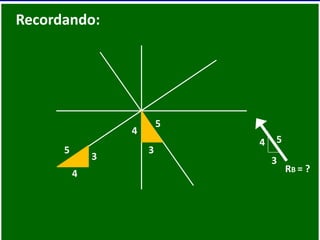
- 78. Recordando: RB = ?4 3 5 3 4 5 3 4 5
- 79. θ = ? P = 100 Kg Q = 50 Kg A B RA = ? RBy RBx n i = 1 RBy = 100 Kg 0 = RBy – 100 + i = 1 Σ Fy = 0
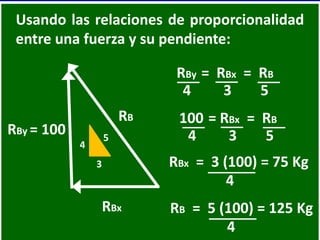
- 80. Usando las relaciones de proporcionalidad entre una fuerza y su pendiente: RB 3 4 5 RBy = 100 RBx RBy = RBx = RB 4 3 5 100 = RBx = RB 4 3 5 RBx = 3 (100) = 75 Kg 4 RB = 5 (100) = 125 Kg 4
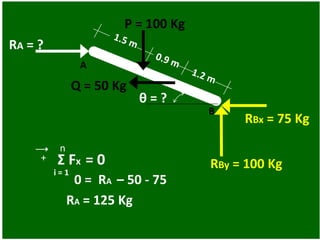
- 81. θ = ? P = 100 Kg Q = 50 Kg A B RA = ? RBy = 100 Kg RBx = 75 Kg n i = 1 RA = 125 Kg 0 = RA – 50 - 75 + i = 1 Σ Fx = 0
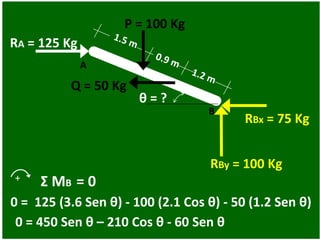
- 82. θ = ? P = 100 Kg Q = 50 Kg A B RA = 125 Kg RBy = 100 Kg RBx = 75 Kg + Σ MB = 0 0 = 450 Sen θ – 210 Cos θ - 60 Sen θ 0 = 125 (3.6 Sen θ) - 100 (2.1 Cos θ) - 50 (1.2 Sen θ)
- 83. 0 = 450 Sen θ – 210 Cos θ - 60 Sen θ 0 = 390 (Sen θ) - 210 (Cos θ) 390 (Sen θ) = 210 (Cos θ) Sen θ = 210 Cos θ 390 Tan θ = 0.5385 θ = Tan¯¹ (0.5385) θ = 28.3° Resp
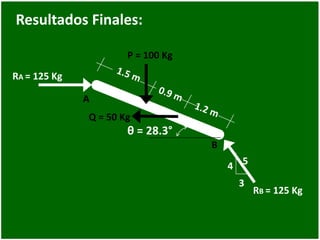
- 84. Resultados Finales: 4 3 θ = 28.3° P = 100 Kg Q = 50 Kg A B RA = 125 Kg 5 RB = 125 Kg
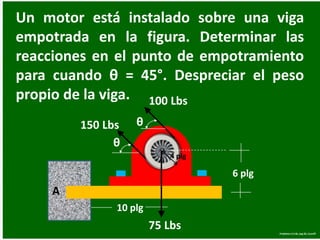
- 85. Un motor está instalado sobre una viga empotrada en la figura. Determinar las reacciones en el punto de empotramiento para cuando θ = 45°. Despreciar el peso propio de la viga. 75 Lbs θ 10 plg 6 plg 100 Lbs A 150 Lbs θ 4 plg Problema 3.3.46, pag 93, Cunniff
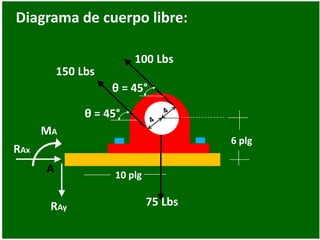
- 86. Diagrama de cuerpo libre: 75 Lbs 10 plg 6 plg 100 Lbs A 150 Lbs θ = 45° RAx RAy MA θ = 45°
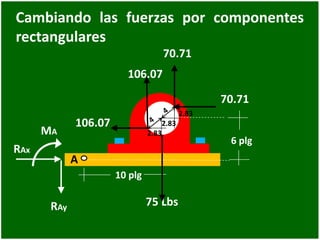
- 87. Cambiando las fuerzas por componentes rectangulares 75 Lbs 10 plg 6 plg 70.71 A 106.07 RAx RAy MA 106.07 70.71 2.83 2.83 2.83
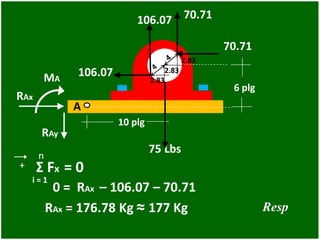
- 88. 75 Lbs 10 plg 6 plg 70.71 A 106.07 RAx RAy MA 106.07 70.71 2.83 2.83 2.83 n i = 1 RAx = 176.78 Kg ≈ 177 Kg 0 = RAx – 106.07 – 70.71 + i = 1 Σ Fx = 0 Resp
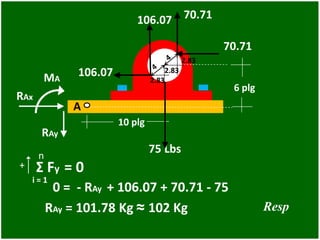
- 89. 75 Lbs 10 plg 6 plg 70.71 A 106.07 RAx RAy MA 106.07 70.71 2.83 2.83 2.83 n i = 1 RAy = 101.78 Kg ≈ 102 Kg 0 = - RAy + 106.07 + 70.71 - 75 + i = 1 Σ Fy = 0 Resp
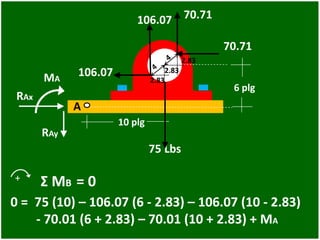
- 90. 75 Lbs 10 plg 6 plg 70.71 A 106.07 RAx RAy MA 106.07 70.71 2.83 2.83 2.83 + Σ MB = 0 0 = 75 (10) – 106.07 (6 - 2.83) – 106.07 (10 - 2.83) - 70.01 (6 + 2.83) – 70.01 (10 + 2.83) + MA
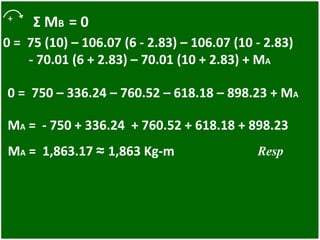
- 91. + Σ MB = 0 0 = 75 (10) – 106.07 (6 - 2.83) – 106.07 (10 - 2.83) - 70.01 (6 + 2.83) – 70.01 (10 + 2.83) + MA 0 = 750 – 336.24 – 760.52 – 618.18 – 898.23 + MA MA = - 750 + 336.24 + 760.52 + 618.18 + 898.23 MA = 1,863.17 ≈ 1,863 Kg-m Resp