Space time
Download as KEY, PDF•0 likes•439 views
This paper proposes an algorithm to optimize the trade-off between space and time for a class of electronic structure calculations involving tensor contractions. The algorithm starts with an operation-based representation and applies transformations to minimize the total memory requirement by reducing the size of intermediate arrays through loop fusion techniques. This approach addresses the challenge of large temporary memory requirements for coupled cluster and other electronic structure models.
![n the class ofrequired. Consider the following expression: be
operations computations considered, the final result to ing to the fused loop to be eliminate
puted can be expressed in terms of tensor contractions, essen- quirement for the computation is to view
a smaller intermediate array and thu
y a collection of multi-dimensional summations of the product loop fusions. Loop fusion merges loop ne
ments. For the example considered
everal input arrays. Due to commutativity, associativity, and loops illustrated in Fig. 1(c). By use loop
into larger imperfectly nested of lo
ributivity, expressionmany different ways to compute the finalnested produces an intermediate array actually be
If this there are is directly translated to code (with ten can be seen that can which is co
in the number arithmetic operations nest, fusing the two loop nests allows the
lt,loops, for could differ widely total number ofof floating point
and they indices ), the
a 2-dimensional array, without chan
rations required. be Consider theif the range of each index
following expression: ing to operations.
the fused loop to be eliminated in t
required will is . a smallerFor a computation comprising of a
intermediate array and thus reduc
Instead, the same expression can be rewritten by use of associative ments.will generally be a number of fusio
For the example considered, the
and distributive laws as the following: illustrated incompatible.By useis because
tually Fig. 1(c). This of loop fus
can berequire different loops to bebe reduc
seen that can actually made th
his expression is directly translated to code (with ten nested a 2-dimensional the problem ofchanging t
ps, for indices ), the total number of arithmetic operations addressed array, without finding the
operations.
operator tree that minimized the tota
uired will be if the range of each index is . For after fusion [14, 16, 15]. of a numb
a computation comprising
ead, the same expression can be rewritten by use of associative will generally be a for manyof fusion choi
However, number of the compu
distributive laws as the the formula sequence shown in Fig. 1(a) and tually compatible. This is because differe
This corresponds to following:
can be directly translated into code as shown in Fig. 1(b). This require different loopscomponent of the NW
coupled cluster
form only requires instances where to be made the outer
operations. However, additional space addressed the problem thefinding the choic minimal memo
and . S=0 fusion is still tooof
S = 0
is required to store temporary arrays T1=0; T2=0;Often, the space operator tree that minimized theIn such sit large.
for b, c
for b, c, d, e, f, l executable implementation, it isspac
requirements for the temporary arrays poses a serious problem. For after fusion [14,0; T2f = 0 T1f =
total ess
T1bcdf += Bbefl Dcdel by for d, 16, 15].
f
only storing lower dimensional s
this example, abstracted from a quantum chemistry model, the ar- However, for e, l of the computation
for b, c, d, f, j, k for many
s corresponds to the indices sequence the largest, while the dfjk
ray extents along formula shown in += T1bcdf and
T2bcjk Fig. 1(a) C extents
are for a, b, c, i, j, k recomputing the befl Dcdel
T1f += B slices as needed. Th
into code as shown in Fig. 1(b). of tempo- coupled clusterwe address in this paper. We
be directly translatedare the smallest. Therefore, the sizeThis
along indices problem component of the NWChem
for j, k
Sabij += T2bcjk Aacik instances whereconceptT1f aCfusion graph
T2f the minimal dfjk
m only requires would dominate theHowever, additional space
rary array operations. total memory requirement. proposed jk += k of memory req
quired to store temporary arrays and (b) Direct implementation
. Often, the space fusion isfor a, i, j, In such situation
still too large.
Sabij += T2fjk A
(a) Formula sequence (unfused code)
uirements for the temporary arrays poses a serious problem. For executable implementation, acik essential
it is
(c) Memory-reduced implementation (fused)
example, abstracted from a quantum chemistry model, thefusion for memory reduction. lower dimensional slices o
Figure 1: Example illustrating use of loop ar- by only storing
extents along indices are the largest, while the extents recomputing the slices as needed. This is th
178
g indices are the smallest. Therefore, the size of tempo- problem we address in this paper. We exten
ussian, NWChem, PSI, and MOLPRO. In particular, they com- The operationproposed concept of a fusion here is a and de
minimization problem encountered graph gen-
array
se the bulk of the computation with thetotal memoryapproach
would dominate the coupled cluster requirement. eralization of the well known matrix-chain multiplication problem,](https://image.slidesharecdn.com/space-time-100609181934-phpapp02/85/Space-time-3-320.jpg)
![so be made fu-
lem discussed in the previous sub-section, requiring that selective
ng fusion edges
Space-Time Tradeoff Exploration
search strategies be developed.
ully fused with
In this paper, we develop a two-step search strategy for explo-
oducer loop for
ration of the space-time trade-off:
n edge (say for
hains for and Search among all possible ways of introducing redundant
loop indices in the fusion graph to reduce memory require-
sented graphi- ments, and determine the optimal set of lower dimensional
ve been added intermediate arrays for various total memory limits. In this
es correspond- step, the use of tiling for partial reduction of array extents is
omplete fusion not considered. However, among all possible combinations
n the scopes of of lower dimensional arrays for intermediates, the combina-
that in fact the tion that minimizes recomputation cost is determined, for a
of or to specified memory limit. The range from zero to the actual
the additional memory limit is split into subranges within which the op-
partial-overlap timal combination of lower dimensional arrays remains the
same.
hm [16, 14] to
s the total stor- Because the first step only considers complete fusion of loops,
s. A bottom-up each array dimension is either fully eliminated or left intact,
intains a set of i.e. partial reduction of array extents is not performed. The
merging solu- objective of the second step is to allow for such arrays. Start-
onfigurations at ing from each of the optimal combinations of lower dimen-
y required un- sional intermediate arrays derived in the first step, possible
s imposed by a ways of using tiling to partially expand arrays along previ-
uration is infe- ously compressed dimensions are explored. The goal is to
g” with respect further reduce recomputation cost by partially expanding ar-
memory. At the rays to fully utilize the available memory
ry requirement](https://image.slidesharecdn.com/space-time-100609181934-phpapp02/85/Space-time-8-320.jpg)
Space time
- 1. CITED BY 9 Space-Time Trade-Off Optimization for a Class of Electronic Structure Calculations Daniel Cociorva Gerald Baumgartner Chi-Chung Lam P. Sadayappan J. Ramanujam Marcel Nooijen David E. Bernholdt Robert Harrison Dept. of Computer and Information Science Department of Chemistry The Ohio State University Princeton University cociorva,gb,clam,saday Nooijen@Princeton.edu @cis.ohio-state.edu Oak Ridge National Laboratory bernholdtde@ornl.gov Dept. of Electrical and Computer Engineering Louisiana State University Pacific Northwest National Laboratory jxr@ece.lsu.edu Robert.Harrison@pnl.gov ABSTRACT : 1. INTRODUCTION The development of high-performance parallel programs for sci- The accurate modeling of the electronic structure of atoms and molecules is very computationally intensive. Many models of elec- entific applications is usually very time consuming. The time to de- tronic structure, such as the Coupled Cluster approach, involve col- velop an efficient parallel program for a computational model can lections of tensor contractions. There are usually a large number be a primary limiting factor in the rate of progress of the science. of alternative ways of implementing the tensor contractions, rep- Our long term goal is to develop a program synthesis system to fa- resenting different trade-offs between the space required for tem- cilitate the development of high-performance parallel programs for porary intermediates and the total number of arithmetic operations. a class of scientific computations encountered in quantum chem- In this paper, we present an algorithm that starts with an operation- istry. The domain of our focus is electronic structure calculations,
- 3. n the class ofrequired. Consider the following expression: be operations computations considered, the final result to ing to the fused loop to be eliminate puted can be expressed in terms of tensor contractions, essen- quirement for the computation is to view a smaller intermediate array and thu y a collection of multi-dimensional summations of the product loop fusions. Loop fusion merges loop ne ments. For the example considered everal input arrays. Due to commutativity, associativity, and loops illustrated in Fig. 1(c). By use loop into larger imperfectly nested of lo ributivity, expressionmany different ways to compute the finalnested produces an intermediate array actually be If this there are is directly translated to code (with ten can be seen that can which is co in the number arithmetic operations nest, fusing the two loop nests allows the lt,loops, for could differ widely total number ofof floating point and they indices ), the a 2-dimensional array, without chan rations required. be Consider theif the range of each index following expression: ing to operations. the fused loop to be eliminated in t required will is . a smallerFor a computation comprising of a intermediate array and thus reduc Instead, the same expression can be rewritten by use of associative ments.will generally be a number of fusio For the example considered, the and distributive laws as the following: illustrated incompatible.By useis because tually Fig. 1(c). This of loop fus can berequire different loops to bebe reduc seen that can actually made th his expression is directly translated to code (with ten nested a 2-dimensional the problem ofchanging t ps, for indices ), the total number of arithmetic operations addressed array, without finding the operations. operator tree that minimized the tota uired will be if the range of each index is . For after fusion [14, 16, 15]. of a numb a computation comprising ead, the same expression can be rewritten by use of associative will generally be a for manyof fusion choi However, number of the compu distributive laws as the the formula sequence shown in Fig. 1(a) and tually compatible. This is because differe This corresponds to following: can be directly translated into code as shown in Fig. 1(b). This require different loopscomponent of the NW coupled cluster form only requires instances where to be made the outer operations. However, additional space addressed the problem thefinding the choic minimal memo and . S=0 fusion is still tooof S = 0 is required to store temporary arrays T1=0; T2=0;Often, the space operator tree that minimized theIn such sit large. for b, c for b, c, d, e, f, l executable implementation, it isspac requirements for the temporary arrays poses a serious problem. For after fusion [14,0; T2f = 0 T1f = total ess T1bcdf += Bbefl Dcdel by for d, 16, 15]. f only storing lower dimensional s this example, abstracted from a quantum chemistry model, the ar- However, for e, l of the computation for b, c, d, f, j, k for many s corresponds to the indices sequence the largest, while the dfjk ray extents along formula shown in += T1bcdf and T2bcjk Fig. 1(a) C extents are for a, b, c, i, j, k recomputing the befl Dcdel T1f += B slices as needed. Th into code as shown in Fig. 1(b). of tempo- coupled clusterwe address in this paper. We be directly translatedare the smallest. Therefore, the sizeThis along indices problem component of the NWChem for j, k Sabij += T2bcjk Aacik instances whereconceptT1f aCfusion graph T2f the minimal dfjk m only requires would dominate theHowever, additional space rary array operations. total memory requirement. proposed jk += k of memory req quired to store temporary arrays and (b) Direct implementation . Often, the space fusion isfor a, i, j, In such situation still too large. Sabij += T2fjk A (a) Formula sequence (unfused code) uirements for the temporary arrays poses a serious problem. For executable implementation, acik essential it is (c) Memory-reduced implementation (fused) example, abstracted from a quantum chemistry model, thefusion for memory reduction. lower dimensional slices o Figure 1: Example illustrating use of loop ar- by only storing extents along indices are the largest, while the extents recomputing the slices as needed. This is th 178 g indices are the smallest. Therefore, the size of tempo- problem we address in this paper. We exten ussian, NWChem, PSI, and MOLPRO. In particular, they com- The operationproposed concept of a fusion here is a and de minimization problem encountered graph gen- array se the bulk of the computation with thetotal memoryapproach would dominate the coupled cluster requirement. eralization of the well known matrix-chain multiplication problem,
- 4. Optimization System Algebraic Transformations Memory Minimization Space-Time Transformation Data Locality Optimization Data Distribution and Partitioning
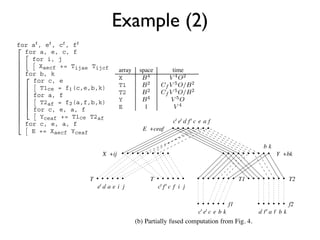
- 5. Fusion Graph can be used to facilitate enumeration of all possible compatible fusion configurations for a given computation tree. The potential for fusion of a common loop among a producer-consumer pair of loop nests is indicated in the fusion graph through a dashed edge connecting the corresponding vertices. ceaf Althoug E +ceaf number of theory gro bk number of X +ij Y +bk and there size of the The fus T T T1 T2 problem, w aei j cf i j the fusion gorithm w f1 f2 and find th cebk af bk and and the size of Figure 5: Fusion graph for unfused operation-minimal form of unable to r loop in Figure 2. arrays wo
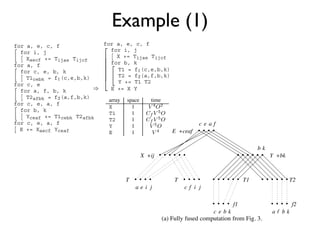
- 6. Example (1) for a, e, c, f for a, e, c, f A desirable solution would be somewhere in bet for i, j for i, j X += Tijae Tijcf fused structure of Fig. 2 (with maximal memory req Xaecf += Tijae Tijcf maximal reuse) and the fully fused structure of Fig. for a, f for b, k T1 = f (c,e,b,k) imal memory requirement and minimal reuse). Thi for c, e, b, k T1cebk = f (c,e,b,k) T2 = f (a,f,b,k) Fig. 4, where tiling and partial fusion of the loops Y += T1 T2 The loops with indices are tiled by splitting for c, e for a, f, b, k E += X Y indices into a pair of indices. The indices with a super T2afbk = f (a,f,b,k) sent the tiling loops and the unsuperscripted indices array space time for c, e, a, f X 1 intra-tile loops with a range of , the block size used for b, k each tile , blocks of and of size T1 1 Yceaf += T1cebk T2afbk puted and used to form product contributions to th T2 1 for c, e, a, f ceaf components of , which are stored in an array of siz Y 1 E += Xaecf Yceaf E +ceaf As the tile size is increased, the cost of function E 1 for decreases by factor , due to the reuse e Figure 3: Use of redundant computation to allow full fusion. ever, the size of the neededb ktemporary array for in X +ij (the space needed for can actually be reduced back Y +bk for a , e , c , f fusing its producer loop with the loop producing E, for a, e, c, f requirement cannot be decreased). When becom for i, j the size of physical memory, expensive paging in an Xaecf += Tijae Tijcf T T T array space time will be required for T1 Further, there are diminishi . T2 for b, k aei j c freuse of i j e for c, e X and after becomes comparable T1ce = f (c,e,b,k) T1 the loop producing now becomes the dominant on for a, f T2 expect that as f1 increased, performance will imp is f2 T2af = f (a,f,b,k) Y level off and then deteriorate. The optimum value of cebk af bk for c, e, a, f E 1 (a) Fully fused computation from Fig. 3. at the various levels o depend on the cost of access Yceaf += T1ce T2af hierarchy. for c, e, a, f The computation consideredgraphs just one com E += Xaecf Yceaf Figure 6: Fusion here is showing re
- 7. T2 1 for c, e, a, f components of , which are stored in Y 1 E += Xaecf Yceaf Example (2) E 1 As the tile size is increased, the for decreases by factor , du Figure 3: Use of redundant computation to allow full fusion. ever, the size of the needed temporar (the space needed for can actually for a , e , c , f fusing its producer loop with the loo for a, e, c, f requirement cannot be decreased). W for i, j the size of physical memory, expens Xaecf += Tijae Tijcf array space time will be required for . Further, the for b, k for c, e X reuse of and after becom T1ce = f (c,e,b,k) T1 the loop producing now becomes for a, f T2 expect that as is increased, perfor T2af = f (a,f,b,k) Y level off and then deteriorate. The op for c, e, a, f E 1 depend on the cost of access at the Yceaf += T1ce T2af hierarchy. for c, e, a, f ct et at f t c e a f E +ceaf The computation considered here E += Xaecf Yceaf term, which in turn is only one bk be computed. Although developers Figure 4: Use of tiling and partial fusion to reduce recomputa- bk naturally recognize and+bk Y perform some tion cost. Y +bk X +ij lective analysis of all these computati implementation is beyond the scope o developments in optimizing compiler reuse of the stored T2 T1 integrals T in and (each element of T and T1 T2 et at a e i j ct f t f i j nificant strides in data locality optimi is used times). However, it is impractical cdue to the existing work that addresses the kind huge memory requirement. With and , the size mization required in the context we c f1 of , is f2 bytes and the size of , is bytes. f1 f2 k By fusing together pairs of producer-consumer loops in the compu- t et c e b k af bk c at f t a f b k tation, reductions in the needed array sizes may Partially fused computation from Fig. 4. n from Fig. 3. (b) be sought, since the fusion of a loop with common index in the pair of loops allows the 4. SOLUTION APPROA elimination of that dimension of the intermediate array. It can be ure 6: Fusion graphs showing redundant compution and tiling. GRAPH
- 8. so be made fu- lem discussed in the previous sub-section, requiring that selective ng fusion edges Space-Time Tradeoff Exploration search strategies be developed. ully fused with In this paper, we develop a two-step search strategy for explo- oducer loop for ration of the space-time trade-off: n edge (say for hains for and Search among all possible ways of introducing redundant loop indices in the fusion graph to reduce memory require- sented graphi- ments, and determine the optimal set of lower dimensional ve been added intermediate arrays for various total memory limits. In this es correspond- step, the use of tiling for partial reduction of array extents is omplete fusion not considered. However, among all possible combinations n the scopes of of lower dimensional arrays for intermediates, the combina- that in fact the tion that minimizes recomputation cost is determined, for a of or to specified memory limit. The range from zero to the actual the additional memory limit is split into subranges within which the op- partial-overlap timal combination of lower dimensional arrays remains the same. hm [16, 14] to s the total stor- Because the first step only considers complete fusion of loops, s. A bottom-up each array dimension is either fully eliminated or left intact, intains a set of i.e. partial reduction of array extents is not performed. The merging solu- objective of the second step is to allow for such arrays. Start- onfigurations at ing from each of the optimal combinations of lower dimen- y required un- sional intermediate arrays derived in the first step, possible s imposed by a ways of using tiling to partially expand arrays along previ- uration is infe- ously compressed dimensions are explored. The goal is to g” with respect further reduce recomputation cost by partially expanding ar- memory. At the rays to fully utilize the available memory ry requirement
- 9. Space-Time optimization Dimension Reduction for Intermediate Arrays search among all possible combination memory and recomputation costs Partial Expansion of Reduced Intermediates resort to array expansion for determining the best choice for array expansion costs
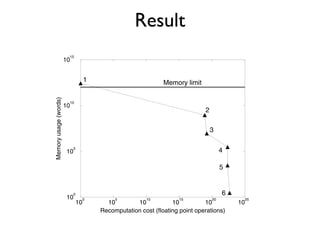
- 10. Result 15 over 10 clus 1 the d Memory limit L sion Memory usage (words) 10 10 2 and anis 3 repe fusi 10 5 4 at m 5 tion and refe 0 6 10 0 5 10 15 20 25 T 10 10 10 10 10 10 Recomputation cost (floating point operations) ory alig by f