Radiciaçâo
Transferir como PPT, PDF•35 gostaram•28,171 visualizações
O documento discute os conceitos fundamentais de radiciação, incluindo: 1) A radiciação é a operação inversa da potenciação e envolve a extração da raiz de um número. 2) Um radical é composto pelo radicando, índice e raiz. 3) As propriedades da radiciação incluem operações com radicais como adição, subtração, multiplicação e divisão.
Radiciaçâo
- 2. Na raiz , temos: = b A radiciação é a operação inversa da potenciação. Ex. 42pois24 2 == n a RADICAL O número n é chamado índice; O número a é chamado radicando; O número b é chamado raiz.
- 3. 3 RadiciaçãoRadiciação Raiz quadrada de um número positivo “a” é o número positivo que elevado ao quadrado dê “a”. Exemplos:Exemplos: 9 3= 49 7= 81 9= 1 1= 0 0= 1,21 1,1= 6,25 2,5= 1 1 4 2 = 0,04 0,2= 636 = 5 3 25 9 =
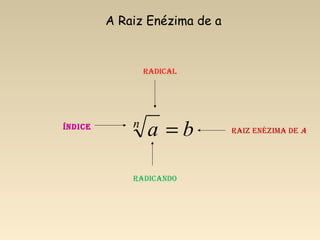
- 4. ban = Radical Radicando Índice Raiz enézima de a A Raiz Enézima de a
- 5. Propriedades daPropriedades da RadiciaçãoRadiciação ( ) aae) aad) aac) 0)(b b a b a b) abbaa) pn pmn m nmn m n mm n n n n nnn = = = ≠= =⋅
- 6. Propriedades dos radicais: nnn babaa ⋅=⋅) Se :,,,,, temosNpNnZmRbRa ++ ++ ∈∈∈∈∈ pn pmn m aab ⋅ ⋅ =) )0() ≠= b b a b a c n n n ( ) n mm n aad =) npp n aae ⋅ =) 3333 102525 =⋅=⋅ 6 423 2.23 2 555 == ⋅ 4 4 4 3 5 3 5 = ( ) ( ) 322288 5 5 3 35 33 5 ==== 6233 777 == ⋅
- 7. Radicais SemelhantesRadicais Semelhantes Dois ou mais radicais são semelhantes,Dois ou mais radicais são semelhantes, quando possuem o mesmo índice e mesmoquando possuem o mesmo índice e mesmo radicandoradicando 32 37 3 54− 3 56− e e
- 8. RADICIAÇÃO Potência com expoente racional Observe as seguintes igualdades: ou Igualmente podemos transformar uma potência com expoente fracionário em um radical. De modo geral, definimos: , com a IR,m,n, IN, a >0, n>0, m>0 Podemos também transformar um radical com expoente fracionário, isto é,vale também a volta. Veja mais um exemplo: 60 13260 13360 133 5 4 4 3 3 2 5 4 4 3 3 2 5 44 33 2 ..... aaaaaaaaaaa ===== ++
- 9. RADICIAÇÃO Potência com expoente racional Propriedade das potências com expoentes racionais As propriedades das potências com expoentes racionais são as mesmas para os expoentes inteiros. Sendo a e b números reais e positivos e os expoentes números racionais, temos que: ( ) n m n m n m n m n m n m q p n m q p n m q p n m q p n m b a b a baba a a a aaa = = = = − + .. .
- 10. SimplificandoSimplificando RadicaisRadicais 23632233223 32233232883b) 22228a) 224 2425 236 336 36 =⋅⋅⋅=⋅⋅⋅ =⋅⋅=⋅= ==== ÷ ÷ Simplificar um radical é reduzir o radicando à sua expressão mais simples. Exemplos:
- 11. RADICIAÇÃO “Introdução” de um fator no radical 33 333 33 567.27.27.2 === Processo prático: 33 33 567.272 == 44 44 300003.10310 == 1805.656 2 == 5005.10510 2 ==
- 12. RADICIAÇÃO Operações com Radicais: Adição e Subtração Exemplo 1: Efetue: Resolução: Os três radicais são semelhantes, pois possuem o mesmo índice 2 e o mesmo radicando 3. Adicionando algebricamente os coeficientes, podemos escrever: 37333 −+ ( ) 32731337333 −=−+=−+ Exemplo 2: Efetue: Resolução: Os três radicais aparentemente não são semelhantes, mas se os simplificarmos, perceberemos que eles são verdadeiramente semelhantes. Simplificando cada um dos radicais, teremos: 1843283 +− 214212242623.42222.33.242223 2253 =+−=+−+−
- 13. RADICIAÇÃO Operações com Radicais: Adição e Subtração Exemplo 3: Efetue: Resolução: Os três radicais aparentemente não são semelhantes, mas se os simplificarmos, perceberemos que eles são semelhantes dois a dois. Simplificando cada um dos radicais, teremos: 864 8112540075 +−+ 536355.235355.25.3 28 46 34 242 +=+−+=+−+
- 14. RADICIAÇÃO Operações com Radicais: Multiplicação Exemplo 1: 5.2 Resolução: Os dois são homogêneos, pois possuem o mesmo índice 2. Multiplicando os radicandos e conservando o índice, podemos escrever: 105.25.2 == Exemplo 2: Efetue: 5 44 33 2 .. aaa Resolução: Os três radicais são heterogêneos, pois possuem índices diferentes. Reduzindo-os ao mesmo índice, teremos: 60 13360 48454060 4860 4560 405 44 33 2 ...... aaaaaaaaaa === E simplificando o radical teremos:60 133 a 60 13260 13120 .. aaaa =
- 17. RADICIAÇÃO Operações com Radicais: Potenciação ( ) 55 35555 3 5 822.2.22.2.22 ==== Logo, ( ) 1.35 3 3 5 1 .22 ← = ( ) 7 67 337 37 3 2 7 3 55.55.55 === Logo, ( ) 3.27 6 2 7 3 .55 ← = ( ) n mr m n r aa = De modo geral, para se elevar um radical a um dado expoente, basta elevar o radicando àquele expoente.
- 18. Radiciação RADICIAÇÃO 2642864 633 === e Logo, 63 2 6464 = 2.3 3813981 4 === e Logo, 42 2 8181 = 2.2 28644096 333 === 2240964096 12 12123 === ou De modo geral, satisfeitas as condições de existência dos radicais envolvidos, podemos indicar a radiciação de um radical assim: nmn m aa . = Operações com Radicais:
- 19. Expressões RADICIAÇÃO =−+=+−+=+−+ 333 984185484182548418 327918811838418 3333 ==+=+=−+= =+= − +=−+ 333 25 4 125 14 25 1115 125 14 25 11 5 3 125 14 5 4 125 64 125 5014 5 2 125 14 333 == + =+= 246416.416.13:5216.13:52 333333 ===== 2 1 3.7.2 3.7 3.7.2 3.23.5 7.3.2 3.25.3 588 1275 22 22 == + = + = +
- 20. RADICIAÇÃO Desenvolvendo Produtos Notáveis ( ) ( )( ) ( ) 246224422222422.2222 22 +=++=++=++=+ ( )( ) ( ) ( ) 36366.36.3363.63 22 −=−=+−+=+− ( ) ( )( ) ( ) ( ) ( ) ( ) 30.213330.21033.103.1010310.310310 222 −=+−=+−−=−−=−
- 21. RADICIAÇÃO Racionalização de Denominadores Em alguns cálculos, você pode se deparar com raízes no denominador da fração, o que a torna irracional. Para que você possa prosseguir com os cálculos, é conveniente que você elimine essas raízes do denominador, esse processo chamado de racionalização de denominadores. Isto é, transforma-se um denominador irracional em racional, para que assim possamos trabalhar com tranquilidade com a fração que agora teremos o denominador é um número irracional e deve ser eliminado. Atenção: o importante é eliminar a raiz (que pode ser quadrada, cúbica, etc), mantendo uma fração "equivalente", ou seja, que representa o mesmo valor. Uma dica é multiplicar tanto o numerador (parte de cima), quanto o denominador pelo mesmo número, o que não interfere na igualdade. Se a fração anterior for multiplicada em cima e em baixo por ficará: Note que é igual a 1, logo a multiplicação de um número por 1 não o altera.
- 22. RADICIAÇÃO Racionalização de Denominadores Prosseguindo: Como se pode notar o denominador agora é um número racional (3).
- 23. RADICIAÇÃO Racionalização de Denominadores Raízes não-quadradas Para eliminar raízes cúbicas, ou de outros índices diferentes de 2 (lembre-se: raiz quadrada é, na verdade, uma raiz de índice 2), é necessário utilizar um artifício. Multiplique, no numerador e no denominador, por uma raiz de mesmo radicando (o número dentro da raiz) e cujo índice seja equivalente ao índice da raiz original, e o expoente do radicando seja o valor do índice menos um. Por exemplo: é o fator racionalizante de ou
- 24. RADICIAÇÃO Racionalização de Denominadores Soma de raízes no denominador Veja: Deve-se multiplicar por Isso porque a multiplicação de por é, na verdade, a multiplicação de (a + b). (a - b), um produto notável, cujo resultado é (a2 - b2 ), isto é, os radicais somem! é o fator racionalizante de é o fator racionalizante de é o fator racionalizante de