nocoes-de-geometria plana ampliada volume 1
- 1. Noções de Geometria Professora: Gianni Leal 6º B.
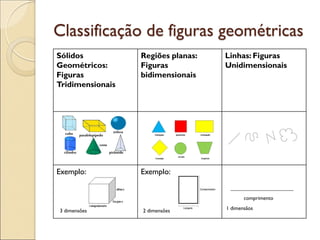
- 2. Figuras geométricas no espaço: mundo concreto e mundo abstrato Mundo concreto: é mundo no qual vivemos e realizamos nossas atividades. Mundo abstrato: é o mundo onde ocorrem pensamentos,reflexões, ideias e também representação mental que fazemos das coisas do mundo concreto. A Geometria é um conhecimento matemático que se desenvolve no mundo abstrato,com base no mundo concreto, real. Coisas do mundo concreto Figuras geométricas Cubos de gelo cubo leque Setor circular mola espiral
- 3. Classificação de figuras geométricas Sólidos Geométricos: Figuras Tridimensionais Regiões planas: Figuras bidimensionais Linhas: Figuras Unidimensionais Exemplo: Exemplo: 3 dimensões 2 dimensões 1 dimensãos comprimento
- 4. Desenhos em 2D e 3D 2D significa bidimensional, um desenho 2D possui imagens planas sem profundidade. Já os desenhos feitos em 3D, que significa tridimensional, possuem profundidade.
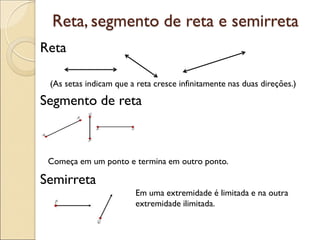
- 5. Reta (As setas indicam que a reta cresce infinitamente nas duas direções.) Segmento de reta Começa em um ponto e termina em outro ponto. Semirreta Reta, segmento de reta e semirreta Em uma extremidade é limitada e na outra extremidade ilimitada.
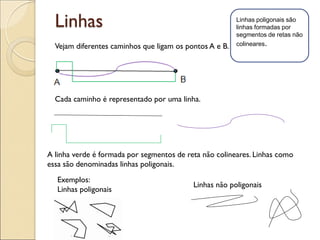
- 6. Linhas Vejam diferentes caminhos que ligam os pontos A e B. Cada caminho é representado por uma linha. A linha verde é formada por segmentos de reta não colineares. Linhas como essa são denominadas linhas poligonais. Exemplos: Linhas poligonais Linhas não poligonais Linhas poligonais são linhas formadas por segmentos de retas não colineares.
- 7. Linhas As linhas podem ser abertas ou fechadas. Linhas abertas: Linhas fechadas: Linhas simples: Linhas não simples:
- 8. Exemplos Classifique as linhas abaixo em: poligonais ou não poligonais, abertas ou fechadas, simples ou não simples. Não poligonal Aberta Não simples Poligonal Fechada Não simples Não poligonal Fechada Simples Poligonal Fechada Não simples Poligonal Fechada Simples Poligonal Aberta Simples Não poligonal Aberta Não simples
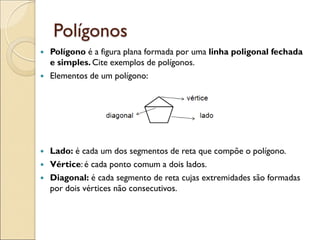
- 9. Polígonos Polígono é a figura plana formada por uma linha poligonal fechada e simples. Cite exemplos de polígonos. Elementos de um polígono: Lado: é cada um dos segmentos de reta que compõe o polígono. Vértice: é cada ponto comum a dois lados. Diagonal: é cada segmento de reta cujas extremidades são formadas por dois vértices não consecutivos.
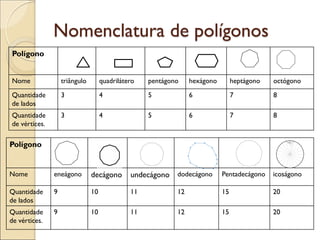
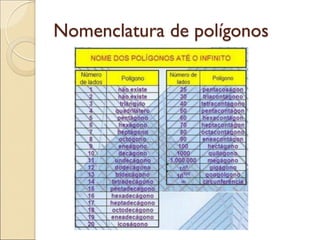
- 10. Nomenclatura de polígonos Polígono Nome triângulo quadrilátero pentágono hexágono heptágono octógono Quantidade de lados 3 4 5 6 7 8 Quantidade de vértices. 3 4 5 6 7 8 Polígono Nome eneágono decágono undecágono dodecágono Pentadecágono icoságono Quantidade de lados 9 10 11 12 15 20 Quantidade de vértices. 9 10 11 12 15 20
- 12. Exercício: Desenhe um: a) Heptágono b) Undecágono c) Quadrilátero d) dodecágono
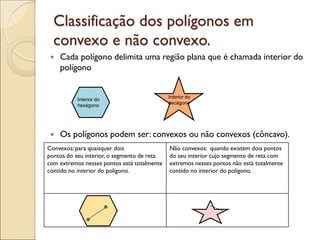
- 13. Classificação dos polígonos em convexo e não convexo. Cada polígono delimita uma região plana que é chamada interior do polígono Os polígonos podem ser: convexos ou não convexos (côncavo). Interior do hexágono Interior do decágono Convexos:para quaisquer dois pontos do seu interior, o segmento de reta com extremos nesses pontos está totalmente contido no interior do polígono. Não convexos: quando existem dois pontos do seu interior cujo segmento de reta com extremos nesses pontos não está totalmente contido no interior do polígono.
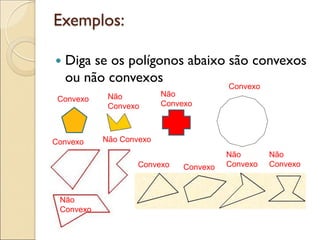
- 14. Exemplos: Diga se os polígonos abaixo são convexos ou não convexos Convexo Convexo Convexo Convexo Convexo Não Convexo Não Convexo Não Convexo Não Convexo Não Convexo Não Convexo
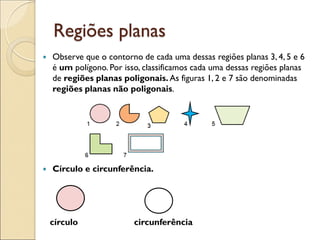
- 15. Regiões planas Observe que o contorno de cada uma dessas regiões planas 3, 4, 5 e 6 é um polígono. Por isso, classificamos cada uma dessas regiões planas de regiões planas poligonais. As figuras 1, 2 e 7 são denominadas regiões planas não poligonais. Círculo e circunferência. círculo circunferência
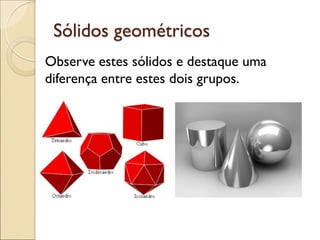
- 16. Sólidos geométricos Observe estes sólidos e destaque uma diferença entre estes dois grupos.
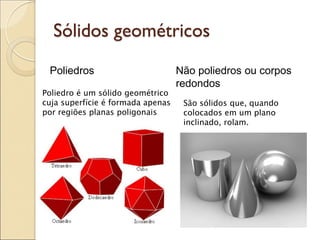
- 17. Sólidos geométricos Poliedros Não poliedros ou corpos redondos Poliedro é um sólido geométrico cuja superfície é formada apenas por regiões planas poligonais São sólidos que, quando colocados em um plano inclinado, rolam.
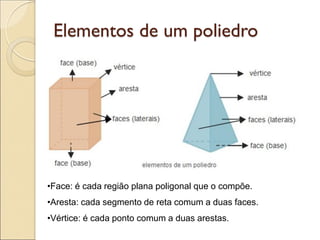
- 18. Elementos de um poliedro •Face: é cada região plana poligonal que o compõe. •Aresta: cada segmento de reta comum a duas faces. •Vértice: é cada ponto comum a duas arestas.
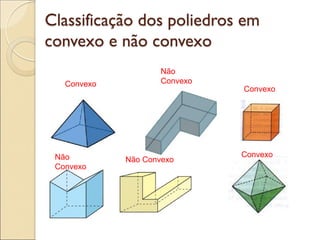
- 19. Classificação dos poliedros em convexo e não convexo Não Convexo Não Convexo Não Convexo Convexo Convexo Convexo
- 20. Cada poliedro delimita uma região do espaço que é denominada região interna. Classificação dos poliedros em convexo e não convexo Poliedros convexos Um poliedro é convexo quando, para quaisquer dois pontos de seu interior, o segmento de reta com extremos nesses pontos está totalmente contido no interior do poliedro. Poliedros não convexos Um poliedro é não convexo quando existem dois pontos do seu interior cujo segmento de reta com extremos nesses pontos não está totalmente contido no interior do poliedro.
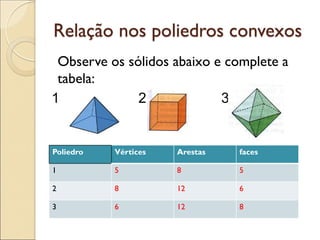
- 21. Relação nos poliedros convexos Observe os sólidos abaixo e complete a tabela: 1 2 3 Poliedro Vértices Arestas faces 1 5 8 5 2 8 12 6 3 6 12 8
- 22. Relação nos poliedros convexos Poliedro Vértices + Faces Arestas + 2 1 5 + 5 8 + 2 2 8 + 6 12 + 2 3 6 + 8 12 + 2 Relação de Euler: Em todos os poliedros convexos, a soma da quantidade de vértices e da quantidade de faces é igual à quantidade de arestas mais duas unidades. Assim, vamos ter: V + F = A + 2, onde V = vértice, F = face e A = aresta.
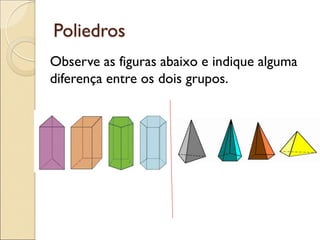
- 23. Poliedros Observe as figuras abaixo e indique alguma diferença entre os dois grupos.
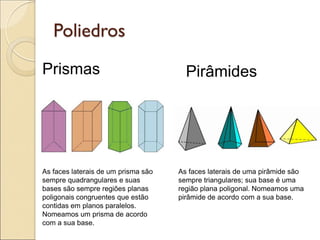
- 24. Poliedros Prismas Pirâmides As faces laterais de um prisma são sempre quadrangulares e suas bases são sempre regiões planas poligonais congruentes que estão contidas em planos paralelos. Nomeamos um prisma de acordo com a sua base. As faces laterais de uma pirâmide são sempre triangulares; sua base é uma região plana poligonal. Nomeamos uma pirâmide de acordo com a sua base.
- 25. Figuras que possuem formato de um prisma
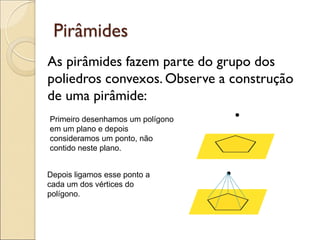
- 26. Pirâmides As pirâmides fazem parte do grupo dos poliedros convexos. Observe a construção de uma pirâmide: • Primeiro desenhamos um polígono em um plano e depois consideramos um ponto, não contido neste plano. Depois ligamos esse ponto a cada um dos vértices do polígono. •
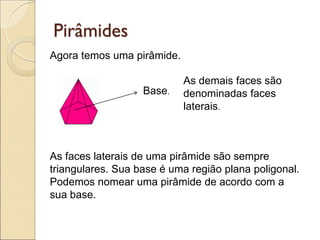
- 27. Agora temos uma pirâmide. Pirâmides Base. As demais faces são denominadas faces laterais. As faces laterais de uma pirâmide são sempre triangulares. Sua base é uma região plana poligonal. Podemos nomear uma pirâmide de acordo com a sua base.
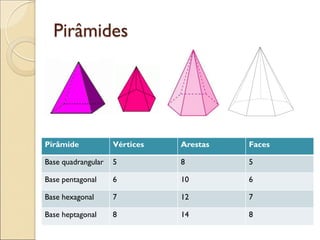
- 28. Pirâmide Vértices Arestas Faces Base quadrangular 5 8 5 Base pentagonal 6 10 6 Base hexagonal 7 12 7 Base heptagonal 8 14 8 Pirâmides
- 29. Figuras que possuem o formato de pirâmide
- 30. Prismas Os prismas também fazem parte do grupo dos poliedros convexos. Observe os prismas apresentados a seguir: faces laterais base Prisma de base triangular Prisma de base pentagonal Prisma de base hexagonal Prisma de base octogonal As faces laterais de um prisma são sempre quadrangulares e suas bases são regiões planas poligonais congruentes que estão contidas em planos paralelos. Nomeamos um prisma de acordo com a sua base.
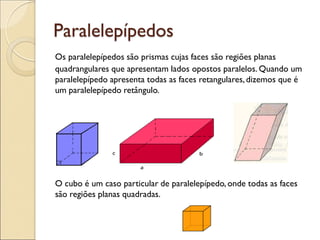
- 31. Paralelepípedos Os paralelepípedos são prismas cujas faces são regiões planas quadrangulares que apresentam lados opostos paralelos. Quando um paralelepípedo apresenta todas as faces retangulares,dizemos que é um paralelepípedo retângulo. O cubo é um caso particular de paralelepípedo, onde todas as faces são regiões planas quadradas.
- 32. Não poliedros ou corpos redondos Os não poliedros mais conhecidos são o cone, o cilindro e a esfera.
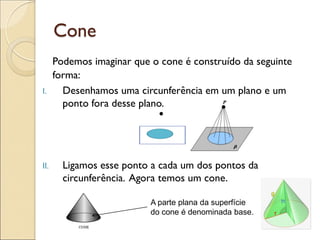
- 33. Cone Podemos imaginar que o cone é construído da seguinte forma: I. Desenhamos uma circunferência em um plano e um ponto fora desse plano. II. Ligamos esse ponto a cada um dos pontos da circunferência. Agora temos um cone. A parte plana da superfície do cone é denominada base.
- 34. Figuras que possuem o formato de um cone Catedral de Maringá Durante o eclipse lunar a terra projeta um cone de sombra no espaço.
- 35. Cilindro Podemos imaginar que um cilindro é construído da seguinte forma: I. Desenhamos uma circunferência em um plano e consideramos um segmento de reta em que um dos extremos é um ponto da circunferência e o outro é um ponto qualquer. II. Traçamos outros segmentos de reta, paralelos e de mesmo comprimento do considerado inicialmente, com um dos extremos em cada um dos outros pontos da circunferência.
- 36. Figuras que possuem o formato cilíndrico
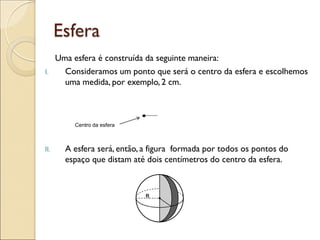
- 37. Esfera Uma esfera é construída da seguinte maneira: I. Consideramos um ponto que será o centro da esfera e escolhemos uma medida, por exemplo, 2 cm. II. A esfera será, então, a figura formada por todos os pontos do espaço que distam até dois centímetros do centro da esfera. Centro da esfera
- 38. Figuras que possuem o formato esférico
- 39. Trabalho para entregar na quarta, dia 11/05. Pesquisar monumentos históricos que tenham formatos geométricos conhecidos, de sólidos. Contornar todos os formatos geométricos conhecidos e nomeá-los. Colocar também o nome do monumento e sua localização. Exemplo: Nome do monumento: Big Bem Localizado em Londres. Nome do sólido: Prisma de base quadrangular Fazer em folha de papel A4 e colocar borda com durex colorido ou pintar a borda.
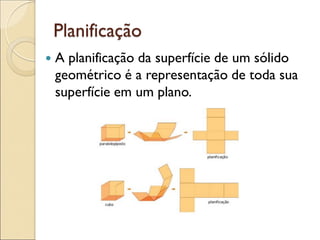
- 40. Planificação A planificação da superfície de um sólido geométrico é a representação de toda sua superfície em um plano.
- 41. Exemplo da planificação do cubo e do tetraedro
- 42. Planificações do cubo A superfície de um mesmo sólido geométrico pode ter várias planificações. Observe as planificações de um mesmo cubo.
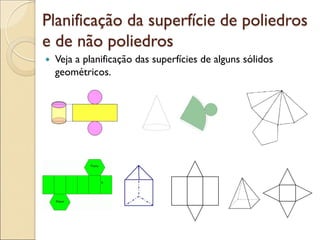
- 43. Planificação da superfície de poliedros e de não poliedros Veja a planificação das superfícies de alguns sólidos geométricos.
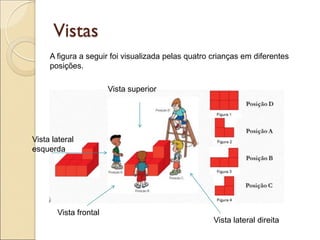
- 44. Vistas A figura a seguir foi visualizada pelas quatro crianças em diferentes posições. Vista frontal Vista superior Vista lateral direita Vista lateral esquerda
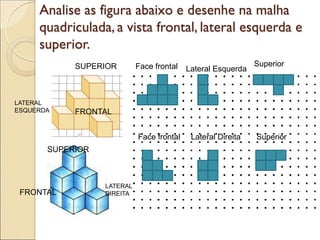
- 45. Analise as figura abaixo e desenhe na malha quadriculada, a vista frontal, lateral esquerda e superior. FRONTAL LATERAL ESQUERDA SUPERIOR FRONTAL LATERAL DIREITA SUPERIOR Face frontal Lateral Esquerda Superior Face frontal Lateral Direita Superior
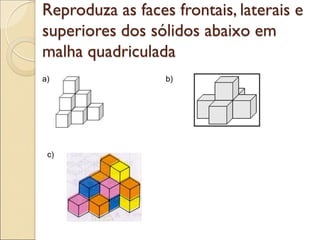
- 46. Reproduza as faces frontais, laterais e superiores dos sólidos abaixo em malha quadriculada a) b) c)
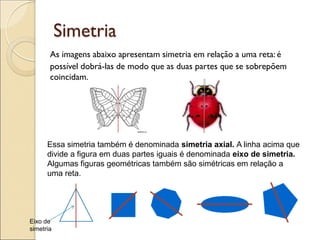
- 47. Simetria As imagens abaixo apresentam simetria em relação a uma reta: é possível dobrá-las de modo que as duas partes que se sobrepõem coincidam. Essa simetria também é denominada simetria axial. A linha acima que divide a figura em duas partes iguais é denominada eixo de simetria. Algumas figuras geométricas também são simétricas em relação a uma reta. Eixo de simetria
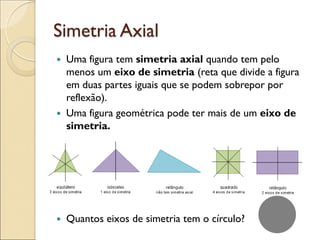
- 48. Simetria Axial Uma figura tem simetria axial quando tem pelo menos um eixo de simetria (reta que divide a figura em duas partes iguais que se podem sobrepor por reflexão). Uma figura geométrica pode ter mais de um eixo de simetria. Quantos eixos de simetria tem o círculo?
- 49. Simetria Axial Solução: O círculo tem infinitos eixos de simetria.
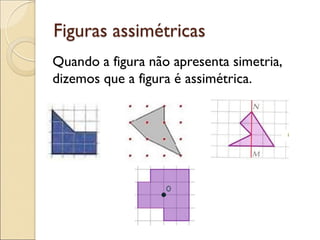
- 50. Figuras assimétricas Quando a figura não apresenta simetria, dizemos que a figura é assimétrica.
- 51. “A natureza está escrita em linguagem matemática.” Formato da Espiral na Via Láctea Formato do Hexágono Formato do Pentágono Formato de Linhas Formato esférico Simetria