Intersecções (GD)
- 2. Intersecção de duas rectas É condição necessária e suficiente para que duas rectas sejam concorrentes que as suas projecções homónimas se intersectem sobre a mesma ordenada
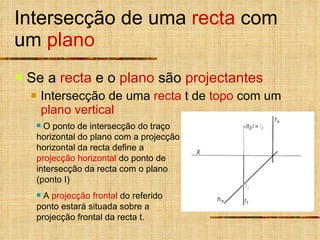
- 3. Intersecção de uma recta com um plano Se a recta e o plano são projectantes Intersecção de uma recta t de topo com um plano vertical O ponto de intersecção do traço horizontal do plano com a projecção horizontal da recta define a projecção horizontal do ponto de intersecção da recta com o plano (ponto I) A projecção frontal do referido ponto estará situada sobre a projecção frontal da recta t.
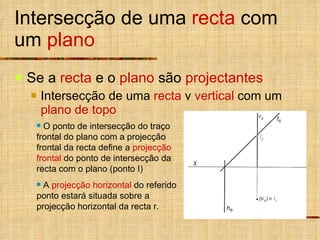
- 4. Intersecção de uma recta com um plano Se a recta e o plano são projectantes Intersecção de uma recta v vertical com um plano de topo O ponto de intersecção do traço frontal do plano com a projecção frontal da recta define a projecção frontal do ponto de intersecção da recta com o plano (ponto I) A projecção horizontal do referido ponto estará situada sobre a projecção horizontal da recta r.
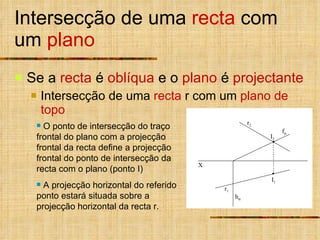
- 5. Intersecção de uma recta com um plano Se a recta é oblíqua e o plano é projectante Intersecção de uma recta r com um plano de topo O ponto de intersecção do traço frontal do plano com a projecção frontal da recta define a projecção frontal do ponto de intersecção da recta com o plano (ponto I) A projecção horizontal do referido ponto estará situada sobre a projecção horizontal da recta r. X r 1 r 2 f h I 1 I 2
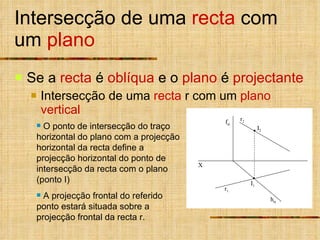
- 6. Intersecção de uma recta com um plano Se a recta é oblíqua e o plano é projectante Intersecção de uma recta r com um plano vertical O ponto de intersecção do traço horizontal do plano com a projecção horizontal da recta define a projecção horizontal do ponto de intersecção da recta com o plano (ponto I) A projecção frontal do referido ponto estará situada sobre a projecção frontal da recta r. X r 1 r 2 f h I 1 I 2
- 7. Intersecção de uma recta com um plano Se o plano não é projectante É necessário considerar um plano auxiliar que contém a recta e determinar a sua intersecção com o plano dado A estudar depois de estudar a intersecção de dois planos
- 8. Intersecção de dois planos A intersecção de dois planos é: Uma recta Um plano (se os planos forem coincidentes) Um conjunto vazio (se os planos forem paralelos)
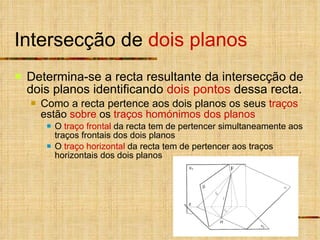
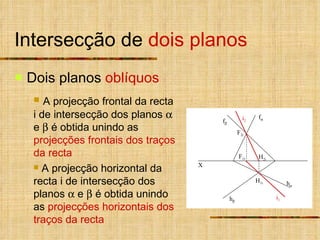
- 9. Intersecção de dois planos Determina-se a recta resultante da intersecção de dois planos identificando dois pontos dessa recta. Como a recta pertence aos dois planos os seus traços estão sobre os traços homónimos dos planos O traço frontal da recta tem de pertencer simultaneamente aos traços frontais dos dois planos O traço horizontal da recta tem de pertencer aos traços horizontais dos dois planos F
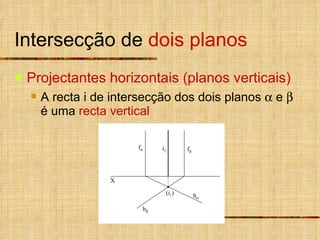
- 10. Intersecção de dois planos Projectantes horizontais (planos verticais) A recta i de intersecção dos dois planos e é uma recta vertical X i 2 (i 1 ) f h f h
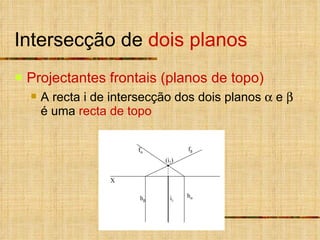
- 11. Intersecção de dois planos Projectantes frontais (planos de topo) A recta i de intersecção dos dois planos e é uma recta de topo X (i 2 ) i 1 f h f h
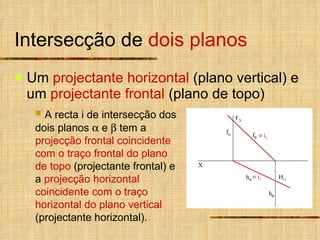
- 12. Intersecção de dois planos Um projectante horizontal (plano vertical) e um projectante frontal (plano de topo) X f h f h A recta i de intersecção dos dois planos e tem a projecção frontal coincidente com o traço frontal do plano de topo (projectante frontal) e a projecção horizontal coincidente com o traço horizontal do plano vertical (projectante horizontal). F 2i H 1i i 2 i 1
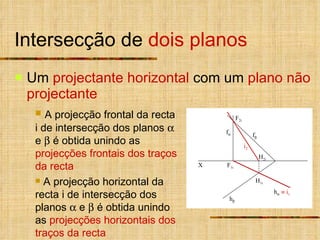
- 13. Intersecção de dois planos Um projectante horizontal com um plano não projectante X f h f h A projecção frontal da recta i de intersecção dos planos e é obtida unindo as projecções frontais dos traços da recta A projecção horizontal da recta i de intersecção dos planos e é obtida unindo as projecções horizontais dos traços da recta F 2i H 1i H 2i F 1i i 2 i 1
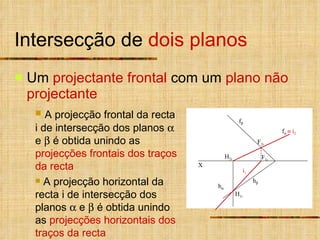
- 14. Intersecção de dois planos Um projectante frontal com um plano não projectante X f h f h A projecção frontal da recta i de intersecção dos planos e é obtida unindo as projecções frontais dos traços da recta A projecção horizontal da recta i de intersecção dos planos e é obtida unindo as projecções horizontais dos traços da recta F 2i H 1i H 2i F 1i i 1 i 2
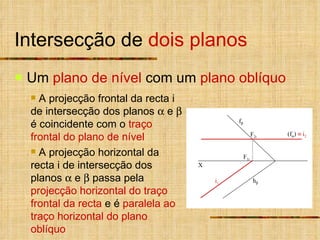
- 15. Intersecção de dois planos Um plano de nível com um plano oblíquo X (f ) f h A projecção frontal da recta i de intersecção dos planos e é coincidente com o traço frontal do plano de nível A projecção horizontal da recta i de intersecção dos planos e passa pela projecção horizontal do traço frontal da recta e é paralela ao traço horizontal do plano oblíquo F 2i F 1i i 1 i 2
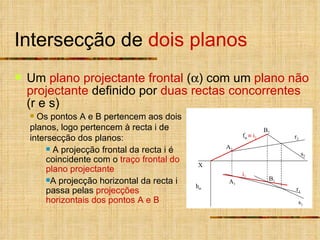
- 16. Intersecção de dois planos Um plano projectante frontal ( ) com um plano não projectante definido por duas rectas concorrentes (r e s) Os pontos A e B pertencem aos dois planos, logo pertencem à recta i de intersecção dos planos: A projecção frontal da recta i é coincidente com o traço frontal do plano projectante A projecção horizontal da recta i passa pelas projecções horizontais dos pontos A e B X f h s 1 r 2 s 2 r 1 i 1 i 2 A 2 A 1 B 2 B 1
- 17. Intersecção de dois planos Dois planos oblíquos A projecção frontal da recta i de intersecção dos planos e é obtida unindo as projecções frontais dos traços da recta A projecção horizontal da recta i de intersecção dos planos e é obtida unindo as projecções horizontais dos traços da recta X f h f h F 2i H 1i H 2i F 1i i 2 i 1
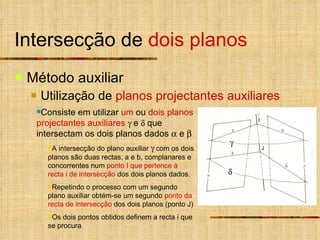
- 18. Intersecção de dois planos Método auxiliar Utilização de planos projectantes auxiliares Consiste em utilizar um ou dois planos projectantes auxiliares e que intersectam os dois planos dados e A intersecção do plano auxiliar com os dois planos são duas rectas, a e b, complanares e concorrentes num ponto I que pertence à recta i de intersecção dos dois planos dados. Repetindo o processo com um segundo plano auxiliar obtém-se um segundo ponto da recta de intersecção dos dois planos (ponto J) Os dois pontos obtidos definem a recta i que se procura J I
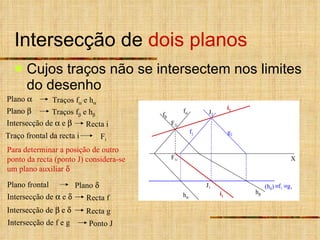
- 19. Intersecção de dois planos Método auxiliar Utilização de planos projectantes auxiliares Este método pode ser utilizado para : determinar a intersecção de dois planos oblíquos cujos traços não se intersectem nos limites do desenho determinar a intersecção de planos definidos por duas rectas concorrentes determinar a intersecção de planos de rampa
- 20. Intersecção de dois planos Cujos traços não se intersectem nos limites do desenho X J 2 J 1 f Para determinar a posição de outro ponto da recta (ponto J) considera-se um plano auxiliar (h ) i 2 i 1 f 1 g 1 f 2 g 2 h f h F 2i F 1i Plano Traços f e h Traço frontal da recta i F i Plano frontal Plano Plano Traços f e h Intersecção de e Recta i Intersecção de e Recta f Intersecção de e Recta g Intersecção de f e g Ponto J
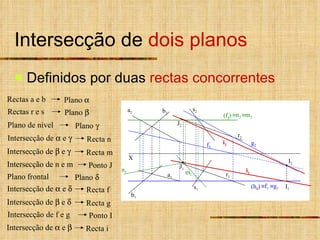
- 21. Intersecção de dois planos Definidos por duas rectas concorrentes X s 1 r 2 s 2 J 2 r 1 J 1 b 1 a 1 b 2 a 2 (f ) I 1 I 2 (h ) n 1 n 2 m 2 m 1 i 2 i 1 f 1 g 1 f 2 g 2 Rectas r e s Plano Plano de nível Plano Plano frontal Plano Rectas a e b Plano Intersecção de e Recta i Intersecção de e Recta n Intersecção de e Recta m Intersecção de e Recta f Intersecção de e Recta g Intersecção de n e m Ponto J Intersecção de f e g Ponto I
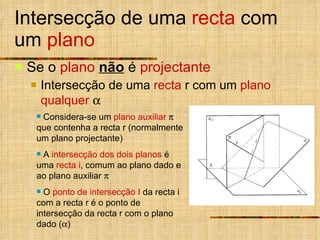
- 22. Intersecção de uma recta com um plano Se o plano não é projectante Intersecção de uma recta r com um plano qualquer Considera-se um plano auxiliar que contenha a recta r (normalmente um plano projectante) A intersecção dos dois planos é uma recta i , comum ao plano dado e ao plano auxiliar O ponto de intersecção I da recta i com a recta r é o ponto de intersecção da recta r com o plano dado ( )
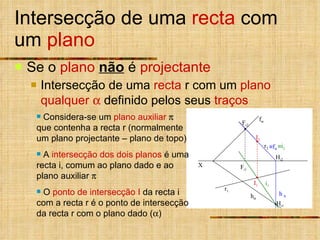
- 23. Intersecção de uma recta com um plano Se o plano não é projectante Intersecção de uma recta r com um plano qualquer definido pelos seus traços X f h r 1 r 2 I 1 I 2 Considera-se um plano auxiliar que contenha a recta r (normalmente um plano projectante – plano de topo) A intersecção dos dois planos é uma recta i, comum ao plano dado e ao plano auxiliar O ponto de intersecção I da recta i com a recta r é o ponto de intersecção da recta r com o plano dado ( ) f h F i2 F i1 H i1 H i2 i 1 i 2
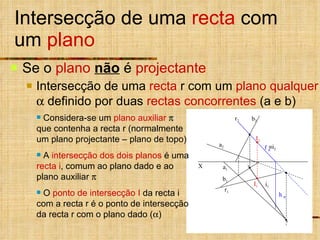
- 24. Intersecção de uma recta com um plano Se o plano não é projectante Intersecção de uma recta r com um plano qualquer definido por duas rectas concorrentes (a e b) Considera-se um plano auxiliar que contenha a recta r (normalmente um plano projectante – plano de topo) A intersecção dos dois planos é uma recta i , comum ao plano dado e ao plano auxiliar O ponto de intersecção I da recta i com a recta r é o ponto de intersecção da recta r com o plano dado ( ) I 1 I 2 f h i 1 i 2 X r 1 r 2 b 1 a 1 a 2 b 2