geometria.pdf
- 2. O QUE É? Geometria é uma área da matemática que se dedica ao estudo das propriedades e relações dos pontos, linhas, ângulos, superfícies e sólidos. Ela tem uma longa história que remonta aos tempos antigos, onde civilizações como os egípcios e os gregos antigos desenvolveram princípios geométricos fundamentais. A geometria tem aplicações em várias áreas, incluindo arquitetura, engenharia, design, física, biologia, ciência da computação e muito mais. Ela desempenha um papel fundamental na compreensão do mundo ao nosso redor e na resolução de uma ampla gama de problemas práticos e teóricos.
- 3. TIPOS DE GEOMETRIA Geometria Euclidiana; Geometria Analítica; Geometria Diferencial; Geometria Não Euclidiana; Geometria Algébrica; Geometria Computacional; A geometria se concentra na descrição e análise das formas, tamanhos e posições dos objetos no espaço. Ela pode ser dividida em várias subáreas, incluindo:
- 4. É a geometria clássica, baseada nas postulados de Euclides, um matemático grego antigo. Ela estuda as propriedades dos objetos no espaço plano e tridimensional, envolvendo conceitos como pontos, linhas, planos, ângulos e figuras como triângulos, quadrados, retângulos e círculos. GEOMETRIA EUCLIDIANA
- 5. Essa abordagem combina a geometria com a álgebra. Ela permite descrever pontos e figuras geométricas através de coordenadas numéricas. Isso permite a análise matemática de objetos geométricos e a resolução de problemas que envolvem equações lineares e sistemas. GEOMETRIA ANALÍTICA
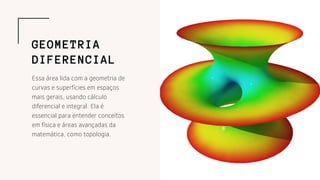
- 6. Essa área lida com a geometria de curvas e superfícies em espaços mais gerais, usando cálculo diferencial e integral. Ela é essencial para entender conceitos em física e áreas avançadas da matemática, como topologia. GEOMETRIA DIFERENCIAL
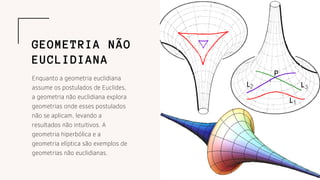
- 7. Enquanto a geometria euclidiana assume os postulados de Euclides, a geometria não euclidiana explora geometrias onde esses postulados não se aplicam, levando a resultados não intuitivos. A geometria hiperbólica e a geometria elíptica são exemplos de geometrias não euclidianas. GEOMETRIA NÃO EUCLIDIANA
- 8. Essa área conecta a geometria com a álgebra, estudando conjuntos de soluções para sistemas de equações polinomiais. Ela é amplamente usada em teoria dos números, criptografia e outras disciplinas. GEOMETRIA ALGÉBRICA
- 9. Utiliza técnicas computacionais para resolver problemas geométricos, como a determinação de interseções entre linhas ou a construção de diagramas de Voronoi. GEOMETRIA COMPUTACIONAL
- 10. GEOMETRIA NA ANTIGUIDADE A geometria desempenhou um papel fundamental na antiguidade e era altamente valorizada por várias civilizações. Aqui estão alguns exemplos de como a geometria foi desenvolvida e aplicada em diferentes culturas antigas Essas civilizações antigas contribuíram para o desenvolvimento da geometria de maneiras distintas, muitas vezes impulsionadas por necessidades práticas, como a construção e a agrimensura. Suas descobertas estabeleceram as bases para o estudo posterior da geometria e influenciaram o desenvolvimento da matemática em todo o mundo.
- 11. Egito Antigo: Os egípcios foram alguns dos primeiros a aplicar princípios geométricos na construção de monumentos e edifícios. Eles usavam medidas precisas para construir pirâmides e templos, utilizando conhecimentos geométricos para calcular áreas, volumes e ângulos. Mesopotâmia: Os matemáticos mesopotâmicos também possuíam conhecimentos geométricos. Eles desenvolveram técnicas para medir áreas de terras agrícolas e para realizar cálculos relacionados à construção e arquitetura. Grécia Antiga: A Grécia antiga é muitas vezes considerada um marco importante na história da geometria. O matemático grego Euclides é famoso por seu trabalho "Os Elementos", um tratado abrangente que apresentava os princípios fundamentais da geometria euclidiana. Ele estabeleceu uma série de axiomas e postulados a partir dos quais derivou muitas proposições geométricas. Além de Euclides, matemáticos gregos como Pitágoras e Arquimedes também contribuíram significativamente para a geometria.
- 12. Geometria na Índia Antiga: A geometria também foi estudada na Índia antiga. Matemáticos indianos desenvolveram técnicas para calcular áreas, volumes e outras propriedades geométricas. Eles também exploraram a geometria com aplicações práticas, como construção de templos e edifícios. Geometria na China Antiga: Os chineses antigos também possuíam conhecimentos geométricos. Eles desenvolveram métodos para medir terras, calcular áreas e resolver problemas práticos usando princípios geométricos.
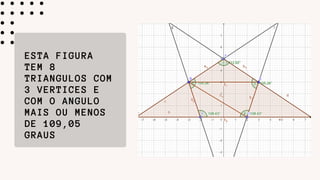
- 13. ESTA FIGURA TEM 8 TRIANGULOS COM 3 VERTICES E COM O ANGULO MAIS OU MENOS DE 109,05 GRAUS