Teorema De PitáGoras
- 1. Informática Educativa II Tutor: Carlos França Grupo: Matematicando na web
- 2. Por: Talita M. Cazagrande
- 3. Na Grécia, por volta do século VI a.C., Pitágoras (580-500 a.C.) fundou uma escola mística secreta chamada Escola Pitagórica. Os membros desta sociedade, os pitagóricos, tinham uma filosofia de vida em que os números apresentavam importância fundamental: a harmonia do universo, o movimento dos planetas, a vida animal e vegetal, o som, a luz, tudo isso só podia ser explicado através dos números. Deve-se a eles a descoberta do famoso Teorema de Pitágoras.
- 4. O Teorema de Pitágoras talvez seja o mais importante teorema de toda a Matemática. Com ele pode-se descobrir a medida de um lado de um triângulo retângulo, a partir da medida de seus outros dois lados.
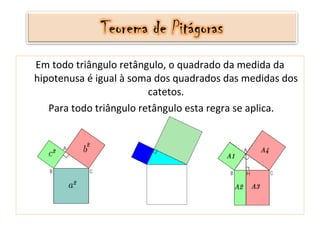
- 5. Triângulo Retângulo É o triângulo que possui um ângulo reto, ou seja, de 90°. Hipotenusa - a Cateto - c Cateto - b
- 6. Em todo triângulo retângulo, o quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos. Para todo triângulo retângulo esta regra se aplica.
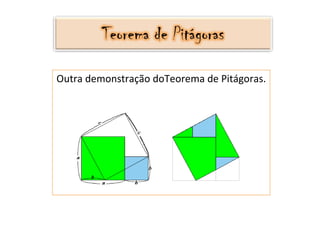
- 7. Outra demonstração doTeorema de Pitágoras.
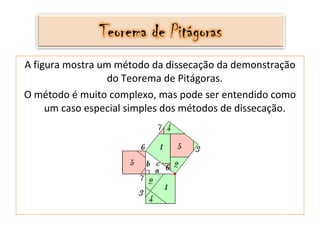
- 8. A figura mostra um método da dissecação da demonstração do Teorema de Pitágoras. O método é muito complexo, mas pode ser entendido como um caso especial simples dos métodos de dissecação.
- 9. O Teorema de Pitágoras e sua relação com circunferências Lunúlas de Hipócrates A figura a seguir mostra um triângulo retângulo e três semi-circunferências tendo os lados como diâmetros. A soma das áreas das duas "lúnulas" é igual à área do triângulo. Sejam: T a área do triângulo, P e Q as áreas das lúnulas e U e V as áreas das outras duas regiões. Como a área do semicírculo sobre a hipotenusa é igual a soma das áreas dos semicírculos construídos sobre os catetos, temos: T + U + V = P + U + Q + V, ou seja, T = P + Q. T P Q U V
- 10. É possível utilizar a regra do Teorema de Pitágoras em praticamente todas as figuras geométricas planas, pois, de alguma forma elas podem ser divididos em triângulos. Por exemplo um quadrado. Podemos determinar a medida da bissetriz de um ângulo interno usando a mesma fórmula, basta perceber que a bissetriz seria a hipotenusa de um triângulo inscrito no quadrado.
- 11. Aplicações Uma escada com 6 metros de comprimento, está encostada a um muro com 4,47 metros de altura, de modo que uma das extremidades da escada encostada à parte de cima do muro. Qual a distância da escada ao muro, medida sobre o chão? Resolução Aplicando o Teorema de Pitágoras : 6 2 = (4,47) 2 + x 2 . Logo , x 2 = 16.0191. Aplicando a raiz quadrada a x , vem : x = 4.0024 m.
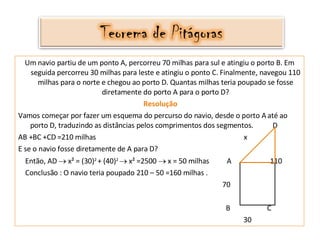
- 12. Um navio partiu de um ponto A, percorreu 70 milhas para sul e atingiu o porto B. Em seguida percorreu 30 milhas para leste e atingiu o ponto C. Finalmente, navegou 110 milhas para o norte e chegou ao porto D. Quantas milhas teria poupado se fosse diretamente do porto A para o porto D? Resolução Vamos começar por fazer um esquema do percurso do navio, desde o porto A até ao porto D, traduzindo as distâncias pelos comprimentos dos segmentos. D AB +BC +CD =210 milhas x E se o navio fosse diretamente de A para D? Então, AD x² = (30) 2 + (40) 2 x² =2500 x = 50 milhas A 110 Conclusão : O navio teria poupado 210 – 50 =160 milhas . 70 B C 30
- 13. Em um recente vendaval, um poste de luz de 9m de altura quebrou-se em ponto a uma distância x do solo. A parte do poste acima da fratura inclinou-se e sua extremidade superior encostou no solo a uma distância de 3m da base do mesmo. A que altura x do solo o poste quebrou? Resolução (9-x)² = x² + 3² 81 – 18x + x² = x² + 9 -18x = 9 – 81 -18x = -72 . (-1) x = 72/18 x = 4m
- 14. INFOESCOLA. TEOREMA DE PITÁGORAS. DISPONÍVEL EM: HTTP://WWW.INFOESCOLA.COM/MATEMATICA/TEOREMA-DE-PITAGORAS. ACESSADO EM 08 JUL. 2008. TEOREMA DE PITÁGORAS. DISPONÍVEL EM: HTTP://WWW.COLEGIOCATANDUVAS.COM.BR/DESGEO/TEOPITAGO/INDEX.HTM ACESSADO EM 08 JUL. 2008 . APLICAÇÕES DO TEOREMA DE PITÁGORAS. DISPONÍVEL EM: HTTP://PACASCARNAXIDE.TRIPOD.COM/EXERCICIOS.HTM ACESSADO EM 08 JUL. 2008. IES. INTERNATIONAL EDUCATION SOFTWARE. PYTHAGREAN THEOREM. DISPONÍVEL EM: HTTP: WWW.MAT.UFG.BR/DOCENTES/JHCRUZ/ENSINO/PITAGORAS.HTM ACESSADO EM 09 JUL. 2008.