TEMA 4b.Energía_y_trabajo.Energía_Y_trabajo.pdf

Tema 4: Trabajo y Energía
©Luis Arrufat Horcajuelo 2019

Tema 4: Trabajo y Energía
GLOSARIO
4.1 CONCEPTO DE ENERGÍA. TIPOS DE ENERGÍA. ENERGÍA MÉCANICA,
CINÉTICA Y POTENCIAL.
4.2 CONCEPTO DE TRABAJO MECÁNICO.
4.3 TEOREMA DE LAS FUERZAS VIVAS. FUERZAS CONSERVATIVAS.
RELACIÓN TRABAJO DE UNA FUERZA-ENERGÍA MECÁNICA.
4.4 PRINCIPIO DE CONSERVACIÓN DE LA ENERGÍA MECÁNICA.

4.1 CONCEPTO DE ENERGÍA. ENERGÍA MECÁNICA, CINÉTICA Y POTENCIAL. .
▪ Partiendo de la base de que la energía se transfiere:
▪ El agua embalsamada tiene energía, produciendo el movimiento de las turbinas y generando
electricidad. → La energía mecánica se transfiere generando energía eléctrica.
▪ Una pila eléctrica tiene energía. Cuando se cierra un circuito eléctrico con una pila y una
lámpara de incandescencia, la energía eléctrica de la pila pasa a la bombilla produciendo luz y
calor. → La energía química se transfiere generando energía lumínica y calorífica.
▪ El muelle comprimido de un bolígrafo tiene energía. Al accionar el pulsador, se libera el muelle
y su energía pasa al pulsador –recupera su posición inicial- y a la punta del bolígrafo que se
oculta. → La energía cinética se transfiere generando energía potencial y viceversa.
▪ El butano tiene energía, por ello cuando se prende el fuego y se coloca una cacerola con agua,
la energía de la llama produce el calentamiento de la cacerola, que a su vez hace que el agua
aumente su temperatura. → La energía química se transfiere generando energía calorífica.

TRABAJO
Así mismo definimos el trabajo como el método o procedimiento para transferir
energía de un sistema a otro, ejerciendo una fuerza sobre éste último a lo largo de
un recorrido. No se trata de energía, sino de un método de transferencia.
CALOR
Un sistema puede transferir a otro energía, por el mero hecho de tener
temperaturas diferentes. A este método de transferencia se le denomina calor.

ENERGÍA MECÁNICA
La energía mecánica es la energía que poseen los cuerpos debido a su posición o su velocidad.
ENERGÍA CINÉTICA
La energía cinética es la energía mecánica que
poseen los cuerpos debido su velocidad.
ENERGÍA POTENCIAL
La energía potencial es la energía mecánica
que poseen los cuerpos debido su posición.
GRAVITATORIA ELÁSTICA
∆EM = ∆Ep + ∆Ec

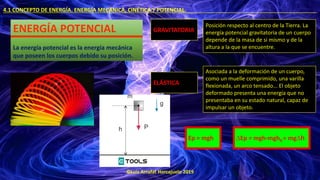
ENERGÍA POTENCIAL
La energía potencial es la energía mecánica
que poseen los cuerpos debido su posición.
GRAVITATORIA
ELÁSTICA
Posición respecto al centro de la Tierra. La
energía potencial gravitatoria de un cuerpo
depende de la masa de si mismo y de la
altura a la que se encuentre.
Asociada a la deformación de un cuerpo,
como un muelle comprimido, una varilla
flexionada, un arco tensado... El objeto
deformado presenta una energía que no
presentaba en su estado natural, capaz de
impulsar un objeto.
Ep = mgh ∆Ep = mgh-mgh0 = mg∆h

Tanto la Energía como el
Trabajo en el SI se mide en
Julios (J), en honor al físico
James Prescott Joule.
Además…
1 caloría = 4,18 Julios
1 kilocaloría = 103 calorías
1 tonelada equivalente de petróleo (tep) = 41,84·109
Julios
1 tonelada equivalente de carbón (tec) = 29,3·109
Julios

EJEMPLO 1.
Dado una bola de 2 kg que deja caer en una pendiente inclinada 45º, cuya altura es de 5 m, y con un
coeficiente de rozamiento dinámico de 0,4 determinar:
a) Fuerza de rozamiento de la bola.
b) Velocidad al final de la cuesta.
c) Variación en la energía potencial.
𝑝
𝑝𝑦
𝑝𝑥
𝐹𝑅
𝑁
45º
1º) Fr=μN=μ·𝑝𝑦= μ mg cos45= 0,4·2·9,8·sqrt(2)/2=5,543 N
2º) 𝑝𝑥-Fr = m· ax → mgsen45-Fr= m·ax
2·9,8·sqrt(2)/2-5,54=2·ax → ax = 4,15 m/s2
v2=v0
2+2as → v=sqrt(02+2·4,15·5/sen(45))=7,66 m/s
3º) ∆Ep=Epf-Ep0=mgh-mgh0={h=0 m; h0=5
m}=2·9,8·0-2·9,8·5=-98 J

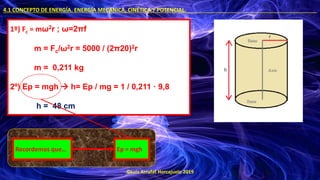
EJEMPLO 2.
Subimos en un ascensor una carga de 2 Toneladas hasta el 6º piso de un edificio. La altura de cada piso es de 2,5
metros. ¿Cuál será la energía potencial al llegar al sexto piso del ascensor?
Ep = mgh {h=2,5·6=15 m} = 2000 · 9,8 · 15 = 294000 J
EJEMPLO 3.
Un cilindro de revolución gira a 20 Hz de frecuencia, teniendo un radio de 1,5 m. Suponiendo que un cuerpo
insertado en el límite exterior de la base superior presenta una fuerza centrípeta de 5000 N con respecto a su
centro, una energía potencial de 1 J, hallar la altura del cilindro.

1º) Fc = mω2r ; ω=2πf
m = Fc/ω2r = 5000 / (2π20)2r
m = 0,211 kg
2º) Ep = mgh → h= Ep / mg = 1 / 0,211 · 9,8
h = 48 cm
Ep = mgh
Recordemos que…

ENERGÍA CINÉTICA
La energía cinética es la energía mecánica que
poseen los cuerpos debido su movimiento.
Con α=1/2 Ec = ½mv2
Precedentes → Teoría de la “vis viva”, Leibniz:
E α mv2
Experimento bloques de arcilla
Invariante física
Se degrada
∆Ec = ½m∆v2 = ½m (v2-v0
2)

EJEMPLO 4.
Calcule cuánto disminuye la energía cinética de un automóvil de 900 kg cuando pasa de 90 a 54 km/h.
= ½900(542-902)/3,62 = -180.000 J
∆Ec = ½m∆v2 = ½m (v2-v0
2)
EJEMPLO 5.
Calcule la energía mecánica que tiene un buitre leonado de 8 kg cuando se encuentra a 150 m de altura, volando
a una velocidad de 60 km/h.

EJEMPLO 5.
Calcule la energía mecánica que tiene un buitre leonado de 8 kg cuando se encuentra a 150 m de altura, volando
a una velocidad de 60 km/h.
Ec = ½mv2 = ½8·602/3,6 = 4000 J
Ep= mgh = 8 · 9,8 · 150 = 11.760 J
EM= Ec + Ep =15.760 J

EJEMPLO BICICLETA. EFECTOS ENERGÍA POTENCIAL Y ENERGÍA CINÉTICA.
Un ciclista de 70 kg se dispone a subir una cuesta de 20 m en 45º con su bicicleta de 10 kg. El
coeficiente de rozamiento de la grava es de 0,4. Determine los siguientes parámetros sabiendo que el
ciclista tarda 30s en alcanzar la máxima altura:
a) Aceleración del sistema en la cuesta.
b) Velocidad al final de la cuesta si parte con una velocidad inicial de 20 km/h
c) Fuerza que ejerce el ciclista.
d) Variación en la energía cinética.
e) Variación en la energía potencial.
f) Variación en la energía mecánica.
g) Energía cinética en el punto más y menos alto.
h) Energía potencial en el punto más y menos alto.
i) Energía mecánica en el punto más y menos alto.

a) Podemos abordar el cálculo de la aceleración mediante un simple cálculo cinemático:
s = v0t + ½at2 =
20
3,6
⋅ 30 +
1
2
𝑎 ⋅ 302 = 20 ➔ a = -0.32 m/s2
b) La velocidad al final de la cuesta será:
v2= v0
2 + 2as = (
20
3,6
)2 + 2·(-0,32)·20 = 4.25 m/s = 15,3 km/h
c) Fuerza que ejerce el ciclista:
Según la dinámica de sistemas→ F-FR-px= ma → {FR = μN = μpy } F – μpy –px = ma
F – μ(M+m)gcosα –(M+m)gsenα = (M+m)a
F – 0,4(70+10)9,8cos45 –(70+10)9,8sen45 = (70+10)(-0.32) → F=806.25 N
d) Variación en la Energía cinética.
∆Ec= ½m∆v2 = ½m (v2-v0
2)=1/2·(70+10)·(4.252-5.552) = -509,6 J → ¡¡Ec SE DEGRADA!!

e) Variación en la Energía potencial:
∆Ep=Ep-Ep0=mgh-mgh0 {tomando h0=0m} = 80·9,8·(20sen45) – 80·9,8·0 = 13342 J
f) Variación en la Energía mecánica
∆EM = ∆Ep + ∆Ec = 12832.5672 J
g) Energía cinética en el punto máximo y mínimo:
Ec (h=0) = ½ 80 · 5.552= 1232.1 J
Ec (h=hmax) = ½ 80 · 4.252= 722.5 J
h) Energía potencial en el punto máximo y mínimo:
Ep (h=0) = 80 · 9,8 · 0 = 0 J
Ep (h=hmax) = 80 · 9,8 · 20sen(45) = 13342 J

i) Energía mecánica en los puntos máximo y mínimo.
EM (h=0) = Ep (h=0) + Ec (h=0) = 1231,1 J
EM (h=hmax) Ep (h=hmax) + Ec (h=hmax) = 14.064, 5 J
OBSERVACIÓN:
Obsérvese que si cogiésemos un objeto y lo dejáramos moverse libremente en una pista en forma de parábola, el
objeto llegaría a un punto en el que se pararía, cuya energía cinética en ese punto sería 0, pero con una energía
potencial de valor mgh caería de nuevo para cobrar velocidad. Al llegar al punto de mínima altura, la energía potencial
sería nula, pero la energía cinética cobraría un valor máximo antes de decelerar debido a la nueva subida. De esta
forma, el cuerpo volvería a alcanzar el máximo valor de energía potencial al llegar al segundo máximo de la parábola
con una energía cinética nula debido a su parón, para así una y otra vez repetir el mismo movimiento.
Si el suelo fuera liso, este movimiento sería perfecto, sin pérdidas caloríficas derivadas de la fricción, haciéndose este
movimiento infinito, pero en la realidad, este movimiento se va amortiguando, hasta que el objeto finalmente se para
en el punto de altura mínima.
Esto nos demuestra dos principios básicos de la energía: su conservación y su degradación.

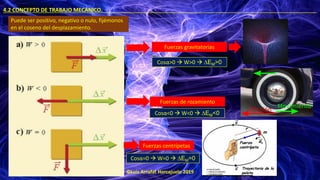
4.2 CONCEPTO DE TRABAJO MECÁNICO. .
Recordemos que el trabajo es un método de transferencia de energía, que consiste en el
desplazamiento del punto de aplicación de una fuerza. Se trata, al igual que la energía, de
una magnitud escalar, con valores negativos, positivos o nulos. Este trabajo se refleja en la
energía mecánica del cuerpo.
Dicho de manera matemática, el trabajo (W) es el producto de una fuerza F por el
desplazamiento de su punto de aplicación, y por el coseno entre esta última y la fuerza; o
visto de otro modo, es el producto de una fuerza F por su proyección sobre su
desplazamiento.
W = Ԧ
𝐹 ⋅ ∆𝑟 · cosα
[W]=[E] en
S.I. → J
1 J = 1 Nm
Trabajo es energía
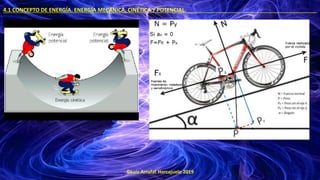
en tránsito

Puede ser positivo, negativo o nulo, fijémonos
en el coseno del desplazamiento.
Fuerzas gravitatorias
Fuerzas de rozamiento
Fuerzas centrípetas
Cosα>0 → W>0 → ∆EM>0
Cosα<0 → W<0 → ∆EM<0
Cosα=0 → W=0 → ∆EM=0

W = F · ∆x ·cosα = 40 · 15 · cos20 = 563,8 J

a) W = F · ∆x ·cosα = 30 · 5 · cos0 = 150 J ; F // ∆x y de igual sentido.
b) W = F · ∆x ·cosα = μ mg · ∆x ·cosα = 0,2 · 10 · 9,8 · 5 cos180 = -98 J;
F // ∆x y de sentido opuesto.
c) RF = F – Fr = 30 – 0,2 · 10 · 9,8 = 10,4 N
d) WT = RF · ∆x · cos α = 10,4 · 5 · cos0 = 52 J
e) Trabajo se invierte en aumentar la energía cinética que parte del reposo → WT=Ec
WT = 1/2mv2 → v = ( 2WT / m)1/2 = ( 2 · 52 / 10)1/2 = 3,224 J

a) W = F · ∆x ·cosα = 8 · 20 · cos60 = 80 J
b) W = F · ∆x ·cosα = 8 · 20 · cos30 = 138,6 J;
c) W = F · ∆x ·cosα = 5 · 20 · cos0 = 100 J;

Si una persona saca de una cubeta de 20 kg y realiza un trabajo de 6 kJ, ¿Cuál es la profundidad del
pozo? Suponga que cuando se levanta la cubeta la velocidad permanece constante.
Pensemos que el trabajo es un método de transferencia de energía, y que la velocidad (y por ende
la energía cinética) permanece constante, con lo que el trabajo queda invertido en la energía
potencial:
W = ∆Ep = mgh – mgh0 = {h0=0} = mgh ➔ h = W / (mg) = 6000 / (20 · 9,8) = 30,622 m

8. Un ascensor tiene 750 kg de masa. ¿Qué trabajo realiza el motor para elevarlo desde el piso
segundo al octavo si la altura de cada piso es de 2,90 m?
T
v
p
Para elevarlo, T>p → p = mg = 750 · 9,8 = 7350 N, luego T>7350 N
El trabajo asociado a T → W = T ∆x cosα = 7350 · (2,90 · 6) ·
cos0º = 127890 J
Es decir, el motor debe ejercer un trabajo mayor a 127890 J
para elevarlo hasta el 8º piso.

PERSONA QUE SUBE, BAJA EN UN ASCENSOR, Y ASCENSOR QUE ROMPE. Suponga una persona de
80 kg de peso sobre una balanza, en un ascensor que sube o baja dependiendo de la situación.
Supongamos que el ascensor subiese en un primer apartado, y que el ascensor pesara 750 kg como
en el anterior ejercicio. Calcular el trabajo desarrollada por la tensión para elevarlo 20 m a 1 m/s2.
T
v
p
a) Lo primero, aclarar, que la persona que está sobre la balanza presenta un equilibrio interno de
fuerzas, es decir, sobre la balanza aplica su peso, y según la tercera ley de Newton, recibe una
fuerza Normal que será la que le de una sensación de peso:
(1) N – p’ = pa = ma ; esto visto desde un enfoque interno, donde pa es el peso
aparente, el que le aparece a la persona en la báscula.
Desde un enfoque externo, la FT, que es la responsable de elevar el ascensor, se mirará
como:
(2) T – p = FT = Ma
Este sistema de ecuaciones nos da como resultado : N = 864 N ; T =8100 N; FT =750 N; pa= 80 N
Luego el trabajo realizado por la tensión será:
W = T · ∆x · cos α = 8100 · 20 · cos0º=16200 J
p’
N

en el anterior ejercicio. Calcular el trabajo desarrollado por la tensión para elevarlo 20 m a 1 m/s2.
Calcular el trabajo desarrollado por la tensión para bajar el ascensor otros 20 metros a 1 m/s2 .
T
v
p
b) En caso de descenso
(1) p’ – N = pa = ma ; esto visto desde un enfoque interno, donde pa es el peso
aparente, el que le aparece a la persona en la báscula.
Desde un enfoque externo, la FT, que es la responsable de descender el ascensor, se
mirará como:
(2) p – T = FT = Ma
Este sistema de ecuaciones nos da como resultado : N = 704 N ; T =6600 N; FT =750 N; pa= 80 N
W = T · ∆x · cos α = 6600 · 20 · cos180º=-132000 J
Observación: Nótese que en el apartado a) elevación → |N|>|p’| ; mientras que en el apartado b)
descenso → |N|<|p’|, además en ambos apartados FT = cte
p’
N

en el anterior ejercicio. Calcular el trabajo desarrollado por el motor para elevarlo 20 m a 1 m/s2.
Calcular el trabajo desarrollado por la tensión para bajar el ascensor otros 20 metros a 1 m/s2 .
T
v
p
c) En caso de rotura de cable → caída libre (20 metros)
(1) p’ – N = pa = ma = mg ; esto visto desde un enfoque interno, donde pa es el
peso aparente, el que le aparece a la persona en la báscula.
Desde un enfoque externo, la FT, que es la responsable de descender el
ascensor, se mirará como:
(2) p – T = FT = Ma = Mg
Este sistema de ecuaciones nos da como resultado : N = 0 N ; T =0 N; FT = p = 7350 N; pa=
784 N
W = T · ∆x · cos α = 0 · 20 · cos180º= 0 J ; el cable se ha roto.
p’
N

4.3 TEOREMA DE LAS FUERZAS VIVAS. FUERZAS CONSERVATIVAS. RELACIÓN TRABAJO DE UNA FUERZA-ENERGÍA MECÁNICA.
1- TEOREMA DE LAS FUERZAS VIVAS.
Este teorema nos demuestra que el trabajo
aplicado por una resultante de fuerzas, RF,
sobre un cuerpo se emplea en variar su
energía cinética.
DEMOSTRACIÓN:
1º) Según las ecuaciones de la cinemática:
v2 – v0
2 = 2a∆s
2º) Multiplicando la expresión por m/2:
ma∆s = ½ m (v2 – v0
2) ; {siendo ma = RF} RF·∆s = ½ m (v2 – v0
2) ; { siendo RF·∆s = W }
W = ∆Ec

EJEMPLO 6
Un automóvil de 1500 kg circula por una carretera rectilínea a 72 km/h. En
un momento dado, acelera y el motor aplica una fuerza resultante de
3000 N durante 100 m. Determine su velocidad final.
____________________________________________________________
SOL
Aplicando el teorema de las fuerzas vivas → W = ∆Ec
F · ∆s = ∆Ec ➔ 3000 · 100 = ½ 1500 (v2 – (72/3,6)2)
v = 101,82 km/h

EJEMPLO 7
Un tenista al sacar ejerce una fuerza de 50 N a lo largo de 45 cm sobre una pelota de 52 g. Calcule: a) El
trabajo aplicado sobre la pelota durante el saque, b) la energía cinética adquirida por la pelota, c) su
velocidad de salida, expresada en km/h.
____________________________________________________________________________________
SOL
Aplicando el teorema de las fuerzas vivas → W = ∆Ec
F · ∆s = ∆Ec ➔ 50 · 0,45 = ½ 0,052 (v2 – 02) ; v0=0, la pelota parte del reposo
al ser golpeada.
v = 105,9 km/h
W = F · ∆s = 22.5 J = Ec – Ec0 = Ec – 0 = Ec

2-TRABAJO Y CAMPOS DE FUERZAS CONSERVATIVOS.
Fuerza conservativa: fuerzas que dependen únicamente de la posición de la
partícula. El trabajo neto es nulo.
Fuerza no conservativa : fuerza que depende de otros parámetros (velocidad,
tiempo, densidad…)
La gravedad que ejerce un cuerpo, depende de su masa y de su radio al cuadrado (posición).
Suponiendo que el cuerpo presenta una masa constante (independiente de otros parámetros), la
gravedad de dicho cuerpo tan solo varía en función de la posición. No es lo mismo, la gravedad en la
superficie de la Tierra, que en la estratosfera, que en esta última queda más atenuada.
Mientras que la fuerza de rozamiento, depende de un parámetro más, que es el coeficiente de
rozamiento, el cual varía generalmente con el tiempo en el movimiento del cuerpo, y el
comportamiento de la fuerza no se conserva.

2-TRABAJO Y CAMPOS DE FUERZAS CONSERVATIVOS.
Ԧ
𝑝 = Ԧ
𝑓 Ԧ
𝑟
𝑊 = Ԧ
𝐹 · ∆𝑟 = | Ԧ
𝐹| · ∆𝑟 cos α ; {∆r = h – h0 ; h>h0}
𝑾𝒑 = | Ԧ
𝐹| · ∆𝑟 cos α = F (h-h0) cos180 = mg (h-h0) cos180
= -∆Ep
Trabajo empleado por la fuerza peso en elevar un cuerpo
Análogamente, trabajo empleado por la fuerza peso al dejar caer un cuerpo:
𝑾𝒑 = | Ԧ
𝐹| · ∆𝑟 cos α = m g (h-h0) cos0 = ∆Ep ; ∆r = h – h0 ; h<h0
La peculiaridad que tienen las fuerzas conservativas, como el peso, es que su trabajo no depende de la trayectoria
realizada, sino de los puntos inicial y final del movimiento.

EJEMPLO 8
Una persona de 72 kg que carga con un carro de la compra con 12 kg de productos, sube
tres pisos de 3 m de altura cada uno. Calcule el trabajo que ha realizado y cuánto ha
incrementado su energía potencial gravitatoria.
𝑾𝑭 = | Ԧ
𝐹| · ∆𝑟 cos α = F (h-h0) cos0 = (M+m) g (h – h0) cos 0 = (72 + 12) · 9,8 · (3·3 – 0)
cos 0 = 7.4 · 103 J = ∆Ep
WF = -Wp

EJEMPLO 9
El motor de un ascensor incrementa la energía potencial de este en un valor de 50.000 J.
Si la masa del ascensor junto con la de los pasajeros es de 1200 kg, determine la altura
que sube.
𝑊𝐹 = | Ԧ
𝐹| · ∆𝑟 cos 𝛼 = F (h-h0) cos0 = M g (h – h0) cos 0 = 1200 · 9,8 · ∆h · cos 0 =
50.000 J = ∆Ep → ∆h = 4,25 m
Imaginemos que después el cable rompe, y el ascensor cae en picado, el trabajo neto de la fuerza peso será el de
subida y el de bajada:
Wp en bajada = mg ∆h cos 0 = 1200 · 9,8 · 4,25 · cos0 = 50.000 J; Wp en subida = - WF = -50.000 J
Wp NETO = Wpsubida + Wpbajada = -50.000 + 50.000 = 0 J → Conservativa

3-EL CASO MÁS GENERAL
En el primer caso, no había efectos en la energía potencial, definiéndose el trabajo de las fuerzas
vivas. En el segundo caso pasaba al revés, la fuerza implicada alteraba exclusivamente la energía
potencial, pero ¿y si se alteran las 2? Por ejemplo en un plano inclinado. Nos encontramos en el
caso general: Entonces, el trabajo invertido en el movimiento se transfiere a ambas energías.
𝑾𝑭 = | Ԧ
𝐹| · ∆𝑟 cos 𝛼 = ∆Ep + ∆Ec
La fuerza implicada no solo altera la energía cinética
del movimiento, sino también su altura.

Este problema está resulto según la definición
de trabajo, pero sabiendo lo anterior, sabemos
que el trabajo queda invertido en una variación
en la energía cinética y en la energía potencial,
por tanto:
∆Ec = ½ m (v2 – v0
2)
∆Ep = mg (h-h0) = 25 · 9,8 · (3,6·sen27-0)
∆Ep =400,42 N
Según la dinámica:
F – mgsen27 = ma
120 – 25·9,8·sen27 = 25 a → a =0,35 m/s2
v2 = v0
2 + 2as ; suponiendo que parte del reposo,
v0 = 0
v = (2as)1/2 = (2·0,35·3,6)1/2 =1,587 m/s
∆Ec = ½ m (v2 – v0
2) = ½ 25 (1,5872 – 02) = 31,48 J
WF = ∆Ec + ∆Ep = 31,48 + 400,42 ≈ 432 J; que como se
comprueba es el trabajo realizado por la fuerza del obrero.

EJEMPLO 10
Se aplica una fuerza sobre un objeto de 10 kg de masa en reposo. La fuerza realiza un
trabajo de 3000 J y, al final, el objeto asciende 20 m por encima del punto de partida.
Determina su velocidad.
SOL 10
∆Ep = mg(h-h0) = 10 · 9,8 · (20 – 0) = 1960 J ; WF = 3000 J
WF = ∆Ep + ∆Ec ➔ 3000 = 1960 + ½ 10 (v2 – 02) → [ 2·(3000 – 1960) / 10 ]1/2 = v = 14,42 m/s

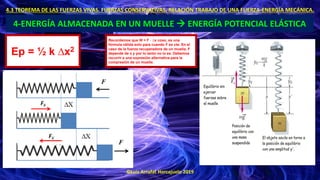
4-ENERGÍA ALMACENADA EN UN MUELLE → ENERGÍA POTENCIAL ELÁSTICA
Ep = ½ k ∆x2
Recordemos que W = F · ∆x cosα, es una
fórmula válida solo para cuando F es cte. En el
caso de la fuerza recuperadora de un muelle, F
depende de x y por lo tanto no lo es. Debemos
recurrir a una expresión alternativa para la
compresión de un muelle.

4-ENERGÍA ALMACENADA EN UN MUELLE → ENERGÍA POTENCIAL ELÁSTICA
Ep = ½ k ∆x2
Recordemos que W = F · ∆x cosα, es una
fórmula válida solo para cuando F es cte. En el
caso de la fuerza recuperadora de un muelle, F
depende de x y por lo tanto no lo es. Debemos
recurrir a una expresión alternativa para la
compresión de un muelle.
EJEMPLO 11
Compresión de 5 cm
Constante de rigidez de 8 N/m
Ep = ½ k ∆x2 = ½ 8 · 0,052 = 0,01 J

4.4 PRINCIPIO DE CONSERVACIÓN DE LA ENERGÍA MECÁNICA .
Partiendo de uno de los principios de la energía: “la energía se conserva”, podemos establecer que cuando hablamos
de energía mecánica, y las disipaciones caloríficas de la energía son nulas, como las debidas a los rozamientos, se
cumple que: ∆EM = 0 → EM – EM0 = 0 → EM = EM0 → ½ mv2 + mgh = ½ mv0
2 + mgh0
EM = cte

Partiendo de uno de los principios de la energía: “la energía se conserva”, podemos establecer que cuando hablamos
de energía mecánica, y las disipaciones caloríficas de la energía son nulas, como las debidas a los rozamientos, se
cumple que: ∆EM = 0 → EM – EM0 = 0 → EM = EM0 → ½ mv2 + mgh = ½ mv0
2 + mgh0
EM = cte
1 El ejemplo más típico es el de la montaña rusa sin disipaciones caloríficas: Una vagoneta de una montaña
rusa, con una masa total de 200 kg, inicia con velocidad nula la bajada en el punto más alto (A) a 18 m de
altura. Cuando alcanza el punto más bajo de la pendiente (B), se encuentra a 3 m de altura e inicia un giro
completo circular de 6 m de diámetro. Calcule: a) Las energías cinética, potencial y mecánica en el punto A.
b) Las energías cinética, potencial y mecánica en el punto B. c) Su velocidad en el punto B expresada en
km/h. d) La energía cinética de la vagoneta en el punto más alto C del tramo circular. e) La velocidad de la
vagoneta en este punto.

a) Ec (A) = ½ m v2 = ½ 200 · 02 = 0 J ; Ep (A) = mgh = 200 · 9,8 · 18 = 35280 J ; EM = Ec + Ep = 35280 J
b) EM (B) = EM (A) = 35280 J = Ec (B) + Ep (B) ; Ep (B) = mgh =200 · 9,8 · 3 = 5880 J ; Ec (B) = EM(B) – Ep(B) = 29400 J
c) Ec (B) = ½ m v2 ➔ v(B) = (2Ec(B)/m)1/2 = 17,14 m/s = 61,72 km/h
d) EM (B) = EM (C) = 35280 J = Ec (C) + Ep (C) = Ec (C) + mgh = Ec(C) + 200 ·9,8· 9 = Ec (C) + 17600 → Ec(C) =17680 J
e) v(C) = (2Ec(B)/m)1/2 = 13 m/s = 58 km/h
1 El ejemplo más típico es el de la montaña rusa sin disipaciones caloríficas: Una vagoneta de una montaña
rusa, con una masa total de 200 kg, inicia con velocidad nula la bajada en el punto más alto (A) a 18 m de
altura. Cuando alcanza el punto más bajo de la pendiente (B), se encuentra a 3 m de altura e inicia un giro
completo circular de 6 m de diámetro. Calcule: a) Las energías cinética, potencial y mecánica en el punto A.
b) Las energías cinética, potencial y mecánica en el punto B. c) Su velocidad en el punto B expresada en
km/h. d) La energía cinética de la vagoneta en el punto más alto C del tramo circular. e) La velocidad de la
vagoneta en este punto.

2 El ejemplo del muelle: Una esfera parte del reposo y cae por efecto de la gravedad desde lo alto de una
superficie cóncava, a 10 m de altura. La esfera pesa 8 kg, y al final de la rampa, se encuentra un resorte de
constante de rigidez de 400 N/m. Calcule la deformación del resorte.

Partiendo del principio de conservación de la energía:
EM = cte → Ec (A) + Ep (A) = Ec (B) + Ep (B);
Como parte del reposo: Ec (A) = 0 J
Energía potencial gravitatoria en el punto más bajo (B) :
h=0 m → Epg (B) = 0 m
Pero observemos que existe en B una energía potencial
elástica → Ep (B) = ½ k x2; siendo x la compresión del
muelle.

Ep (A) = Ec (B) + Ep (B)
mgh(A) = ½ mvB
2 + ½ k x2
Al llegar al resorte, la bola es detenida, siendo v(B) = 0
m/s → Ec(B) = 0 J.
mgh(A) = ½ k x2
8 · 9,8 · 10 = ½ 400 · x2
x = 2 m

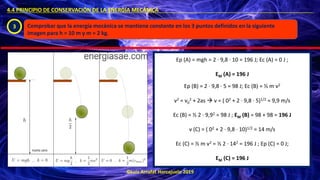
3 Comprobar que la energía mecánica se mantiene constante en los 3 puntos definidos en la siguiente
imagen para h = 10 m y m = 2 kg.
Ep (A) = mgh = 2 · 9,8 · 10 = 196 J; Ec (A) = 0 J ;
EM (A) = 196 J
Ep (B) = 2 · 9,8 · 5 = 98 J; Ec (B) = ½ m v2
v2 = v0
2 + 2as → v = ( 02 + 2 · 9,8 · 5)1/2 = 9,9 m/s
Ec (B) = ½ 2 · 9,92 = 98 J ; EM (B) = 98 + 98 = 196 J
v (C) = ( 02 + 2 · 9,8 · 10)1/2 = 14 m/s
Ec (C) = ½ m v2 = ½ 2 · 142 = 196 J ; Ep (C) = 0 J;
EM (C) = 196 J

TEMA 4b.Energía_y_trabajo.Energía_Y_trabajo.pdf

Más contenido relacionado

Similar a TEMA 4b.Energía_y_trabajo.Energía_Y_trabajo.pdf (20)

Más de luisarrufat97 (20)

Último (20)

TEMA 4b.Energía_y_trabajo.Energía_Y_trabajo.pdf