Elementos a flexo compresion
- 1. DISEÑO DE ACERO Y MADERA CURSO: DISEÑO DE ACERO Y MADERA TEMA: Elementos en flexo compresión ALUMNO NORBIL AGUILAR ÁGUILA PROFESOR ING: CLAUDIO LOPEZ GUTIERREZ
- 2. ELEMENTOS EN FLEXO - COMPRESION INTRODUCTION: En las estructuras reales, la mayor parte de las columnas, en adición a la carga axial, deben soportar cargas laterales y transmitir momentos entre sus extremos y quedan entonces sometidas a esfuerzos combinados debidos a carga axial y a momento. Tales miembros se llaman vigas - columnas. Los momentos en los extremos pueden ser causados por una acción continua de marco o por la excentricidad de las cargas longitudinales OBJETIVOS: Determinar los elementos sometidos a los diferentes tipos de en flexo - compresion ÍNDICE: a. Elementos en flexo compresión.Fórmulas racionales y fórmulas empíricas.Fórmulasde interacción del AISC. b. Efectos de momento secundario por deformación delelemento. c. Ejemplo de una columna de un edificio. d. Ejemplo de una columna de un pórtico de gran luz,donde prima la flexión.
- 3. INTRODUCTION: ELEMENTOS EN FLEXO - COMPRESION En las estructuras reales, la mayor parte de las columnas, en adición a la carga axial, deben soportar cargas laterales y transmitir momentos entre sus extremos y quedan entonces sometidas a esfuerzos combinados debidos a carga axial y a momento. Tales miembros se llaman vigas-columnas. Los momentos en los extremos pueden ser causados por una acción continua de marco o por la excentricidad de las cargas longitudinales o por la excentricidad de las cargas longitudinales Elemento que trabaja como viga-columna Las columnas en los marcos de un edificio,en adición a las cargas vivas y muertas de la estructura arriba de cualquier nivel,a menudo deben transmitir momentos flexionantes que resultan por carga de viento o fuerzas laterales de inercia debidas a sismos. Deben resistir también los momentos de extremo introducidos a través de la acción continua de marco de las vigas cargadas adyacentes que se conectan a ellas. En marcos de edificios, los momentos inducidos por la deflexiónlateral de la estructura deben incluirse también. Un miembro cargado excéntricamente del tipo mostrado en la figura 4.2.a se deflexionara típicamente como se ilustra en la curva carga-deflexión mostrada en la figura 4.2.b. Si la viga-columna fuese a responder elásticamente, y si el momento adicional debido a la fuerza P multiplicada por la deflexiónΔse ignorase, la respuesta sería lineal,como se indica con la línea recta delgada. Sin embargo, el momento adicional PΔ causa una mayor deflexióny esta su vez causa un mayor momento, de manera que la curva de cargadeflexión se vuelve no lineal(paracada incremento de P resulta una Δ mayor).
- 4. Figura 4.2.a Viga columna Figura 4.2.b Curva carga-deflexión Eventualmente, las fibras exteriores del miembro empiezan a fluir,agregando otra componente al comportamiento no lineal.Finalmente,la resistencia interna no puede mantener el paso con la fuerza P aplicada externamente y la curva de carga-deflexión alcanza un pico. Esta es la fuerza máxima que puede ser encontrada mediante la ecuación de interacción del LRFD. Esta ecuación se presenta a continuación : Esta ecuación nos permite saber si nuestra viga-columna es satisfactoria, esto sucederá si se cumple la ecuación H1-1a del LRFD, o bien la ecuación H1-1b del LRFD según sea el caso. Donde: Pu: fuerza requerida determinada por análisis estructural para las cargas factorizadas. Øc:0.85 es el factor de resistencia para columnas si la fuerza axial es de compresión. Pn: capacidad nominal axial, incluida la influenciade la relación de esbeltezy del pandeo local. Esta es la carga que el miembro puede soportar si sólo la carga axial fuese a actuar. Øb= 0.9,es el factor de resistencia por flexión.
- 5. Mnx , Mny :capacidad nominal por flexión,que incluye los efectos de pandeo local y del pandeo lateral torsional, si es que hay. Estos son los momentos que el miembro puede soportar si sólo están presentes momentos flexionantes. Mux, Muy: momentos requeridos respecto a los ejesx, Y y, tal como son determinados por el análisisestructural, incluyendo los efectos de segundo orden debido a los momentos adicionales causados por la fuerza axial multiplicada por la deflexión(Mux o Muy= B1Mnt+ B2Mtl). Momento de no traslación(Mnt), el cual ocurre cuando el marco esta arriostrado por lo que no hay desplazamiento lateral. Esto se ilustra en la figura 4.3. Momento de traslación lateral( Mtl),es causado por cargas laterales o por las cargas de gravedad no balanceadas. Debido a que las juntas se trasladan gracias a que no esta impedido el alabeo en la parte de arriba de la viga- columna(ver figura 4.4). Las cargas de gravedad pueden producir un desplazamiento lateral si el marco es asimétrico o si las cargas de gravedad están asimétricamente colocadas. Mtl será cero si el marco esta arriostrado
- 6. Por otro lado, la presencia de carga axial en una viga-columna produce momentos secundarios o de segundo orden, que consisten en momentos que aparecen después de que se ha desplazado la viga-columna. Estos efectos se pueden ver en la figura 4.5 MOMENTOS SECUNDARIOS O DE SEGUNDO ORDEN Como un análisis de segundo orden es un poco difícil, ya que consiste en ir iterando el incremento de momento cada vez que aparece una nueva deflexión, se utilizará un análisis elástico de primer orden amplificando los momentos obtenidos con los factores de amplificación llamados B1 y B2. De manera que el momento final en un miembro particular será: Mu= B1Mnt+ B2Mtl
- 7. Donde: B1:factor de amplificación para tomar en cuenta el efecto Pδ B2: factor de amplificación para tomar en cuenta el efecto PΔ OBTENCIÓN DE B1. B1=1 cuando la deflexión mayor se encuentra en el centro ,pero, debido a que la curvatura simple tiene deflexiones mayores que un miembro en curvatura doble a elementos que presenten esta última seránecesario reducir B1 yaque si no lo hacemos ,estaremos sobreamplificando el momento, y caeríamos en el error de tratar a un elemento con curvatura doble como si estuviera en curvatura simple. Esto se explicara mediante la figura 4.6 distribución de momentos en una viga columna Por lo anterior el momento máximo en una viga dependerá de la distribución del momento flexionante a lo largo del miembro. La distribución del momento flexionante a lo largo del miembro se tomará en cuenta por medio de un factor Cm. El factor Cm se aplica a la condición arriostrada. Hay dos categorías de miembros; aquellos que poseen cargas transversales aplicadas entre los extremos y aquellos sin cargas transversales.
- 8. 1. Cm cuando no hay cargas transversales actuando en el miembro(ver figura ) M1/M2 es la razón de los momentos flexionantes en los extremos del miembro. M1 es el momento de extremo menor en el valor absoluto, M2 es el mayor y la razón es positiva para los miembros flexionados en curvatura doble y negativa para flexión de curvatura simple, tal y como se presenta en la figura 4.8.La curvatura doble ocurre cuando M1 y M2 son ambos horarios o ambos antihorarios.
- 9. Convención de signos para la relación M1/M2 2 Cm cuando hay cargas transversales actuando en el miembro a) Para miembros con extremos restringidos Cm=0.85 b) Para miembros con extremos no restringidos Cm=1.0 OBTENCIÓN DE B2. En una viga columna cuyos extremos tienen libertad de trasladarse, el momento primario resultante del desplazamiento lateral está casi siempre en el extremo. Como consecuencia de esta condición, los momentos máximos son aditivos y no se requiere el factor Cm(es igual a 1).Aquí, los momentos iguales de extremo son causados por el desplazamiento lateral(por la carga horizontal).La carga axial, que resulta parcialmente de cargas que no causan desplazamiento lateral, es transmitida y amplifica el momento de extremo. Esto se observa en la figura
- 10. El factor de amplificación B2 para los momentos por desplazamiento lateral, esta dado por cualquiera de las 2 ecuaciones que se presentan abajo: Donde: ∑Pu= suma de las cargas factorizadas sobre todas las columnas en el piso bajo consideración. ∆OH= ladeo(desplazamiento lateral)del piso bajo consideración. ∑H= suma de todas las fuerzas horizontales que causan ∆OH. L= altura del piso ∑Pe2= suma de las cargas de Euler para todas las columnas en el piso (al calcular Pe2 use KL/r para el eje de flexión y un valor de K correspondiente a la condición no arriostrada).
- 11. FÓRMULAS DE INTERACCIÓN DEL AISC. La FLEXO - COMPRESION. Corresponde entonces a continuación considerar el caso de columnas con excentricidad, seaestacausada por imperfecciones de la propia columnas o por momentos aplicados. Generalmente en estos casos el pandeo ocurre de inmediato, al aplicar el momento P*e siendo “P” la carga y “e” la excentricidad. Columna con Excentricidad FORMULAS Matemáticamente se resuelve este caso con la llamada Formula de la Secante donde: ymax = e*(sec (mL/2) -1) donde m = √(P/E*I), o sea que ymax = e*(sec (√(P/E*I)*(L/2) -1)) llegando finalmente, al aplicar Euler, a: ymax = e*(sec (√(P/Pcr)*(π/2) -1)) y como el momento máximo ocurre en el centro de “L” : M= P*(e + ymax) Por lo que solo nos resta sustituir ymax en la ecuación y donde el procedimientode diseño consistía en asumir un Fy y tomar un valor por Norma.
- 12. Para el calculo de columnas a FLEXO - COMPRESION se emplean hoy día las Formulas de Interacción que toman en cuenta la acción simultanea de la carga axial y del momento flector tanto en el rango elástico como en el rango plástico a saber: P/P0 + M/M0 ≤ 1 donde P y M= Carga Axial y Momentos actuantes P0 y M0 = Resistencia a compresión simple y flexión simple. Usando factores adecuados se pueden escribir las siguientes formulas. P/A*F.S. = fa = esfuerzo de trabajo bajo carga axial de diseño P0/A*F.S.=Fa = esfuerzopermisibleporcompresiónsimple(comosi soloexistiesecargaaxial) M/S*F.S. = fb = esfuerzo de trabajo por flexión bajo la carga de diseño M0/S*F.S. = Fb = esfuerzo permisible para flexión pura (como si solo hubiesen momentos flectores) Luego la formula de Interacción seria: fa / Fa + fb / Fb ≤ 1 Caso de la Viga – Columna Ha sido demostrado en las vigas – columna que y = y0(1/[1-(P/Pcr)]) donde
- 13. y0 = Flecha de la viga sin carga axial (por imperfección, excentricidad, flecha inicial, etc.) P = Carga axial actuante Pcr = Carga critica de Euler 1/[1-(P/Pcr)] = Factor de Amplificación Por consiguientesi enlavigaactúaun momentoinicialMbdebidoacarga otroefectoimplica que: M = Mb* Factor de Amplificación Entonces nos queda la formula de Interacción de la siguiente manera: P/P0 + Mb /M0*Factor de Amplificación ≤ 1 El American Institute for Steel Construction (A.I.S.C.) considera tres (03) casos: Caso I : Cuando la carga axial es pequeña y se permite no tomar en cuenta el factor de amplificación y cuando la carga axial es apreciable. Es decir: fa / Fa + fb / Fb ≤ 1 cuando fa / Fa ≤ 0,15 Caso II: Cuando fa / Fa ≥ 0,15 quedaría de la siguiente manera: fa / Fa + Cm*fb /(1-fa/Fe’)*Fb ≤ 1 donde: Cm = αm (Norma) = Factor de equivalencia que toma en cuenta las diferentes condicionesde apoyo y tipos de carga. Para el caso que nos ocupa Flexo – Compresión: Caso II: Para casos con desplazamiento lateral (pórticos no arriostrados lateralmente): Cm = αm (Norma) = 0,85 (fijo)
- 14. Fe’ = Esfuerzo critico (Rango Elástico, Euler) Fe’ = fcr/F.S. Para casos sin desplazamiento lateral (pórticos arriostrados lateralmente): Cm = αm (Norma) = 0,6 –(0,40)(M1/M2) ≥ 0,40 (No menor que 0,4) Caso III : Cuando fa / Fa > 0,15 en puntos arriostrados en el plano de flexión. Es decir: fa /0,6Fy + fb / Fb ≤ 1 Este caso esta previsto para vigas-columna donde la máxima combinación de esfuerzos por carga axial y flexión pueden mantenerse en un extremo arriostrado y no en los puntos intermediosdel miembrodonde se magnificanlosmomentos.EnlaNormaCOVENIN,pagina35 se hallan estas mismas formulas expresadas en los casos en los que hay flexión en ambos sentidos ortogonales. Según la Norma COVENIN Fe’ = 10.8x106 /(K*Lb/rb)2 y donde Lb = es la longitud no arriostrada en el plano de la flexión y rb es el correspondiente radio de giro.
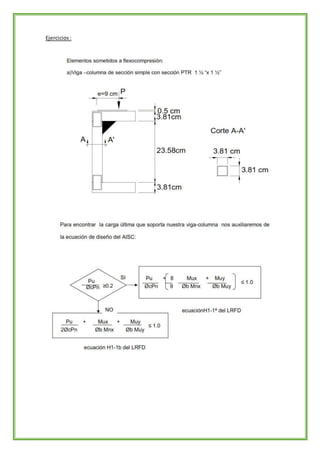
- 15. Ejercicios :
- 16. A continuación se proponen valores de carga incrementando paulatinamente el valor de la carga Pu ;así como también el momento Mu, a partir de considerar una excentricidad de 9 cm para el ensaye Tabla 6.3Resistencia de una viga-columna de sección simple
- 17. A continuación se muestran la instrumentación del ensaye a flexocompresión del elemento con sección simple. Viga-columnade secciónsimplesometida a flexocompresión montada en el gato hidráulico . Momento en el que la viga-columna con sección simple sometida a flexocompresión falla debido a una carga Pu de 2090 kg. b) Viga –columna de sección compuesta con sección PTR 1 ½ “x 1 ½”
- 18. A continuación se muestran la instrumentación del ensaye a flexocompresión del elemento de sección compuesta.
- 19. Viga-columna de sección compuesta sometida a flexocompresión montada en la máquina universal de compresión con capacidad de 50 toneladas. Estado final de la viga-columna de sección compuesta . La falla del elemento ocurrió con una Pu de 4200 kg 2) ejercicios











![Para el calculo de columnas a FLEXO - COMPRESION se emplean hoy día las Formulas de
Interacción que toman en cuenta la acción simultanea de la carga axial y del momento flector
tanto en el rango elástico como en el rango plástico a saber:
P/P0 + M/M0 ≤ 1
donde P y M= Carga Axial y Momentos actuantes
P0 y M0 = Resistencia a compresión simple y flexión simple.
Usando factores adecuados se pueden escribir las siguientes formulas.
P/A*F.S. = fa = esfuerzo de trabajo bajo carga axial de diseño
P0/A*F.S.=Fa = esfuerzopermisibleporcompresiónsimple(comosi soloexistiesecargaaxial)
M/S*F.S. = fb = esfuerzo de trabajo por flexión bajo la carga de diseño
M0/S*F.S. = Fb = esfuerzo permisible para flexión pura (como si solo hubiesen momentos
flectores)
Luego la formula de Interacción seria:
fa / Fa + fb / Fb ≤ 1
Caso de la Viga – Columna
Ha sido demostrado en las vigas – columna que
y = y0(1/[1-(P/Pcr)]) donde](https://image.slidesharecdn.com/elementosaflexocompresion-160516212716/85/Elementos-a-flexo-compresion-12-320.jpg)
![y0 = Flecha de la viga sin carga axial (por imperfección, excentricidad, flecha inicial, etc.)
P = Carga axial actuante
Pcr = Carga critica de Euler
1/[1-(P/Pcr)] = Factor de Amplificación
Por consiguientesi enlavigaactúaun momentoinicialMbdebidoacarga otroefectoimplica
que:
M = Mb* Factor de Amplificación
Entonces nos queda la formula de Interacción de la siguiente manera:
P/P0 + Mb /M0*Factor de Amplificación ≤ 1
El American Institute for Steel Construction (A.I.S.C.) considera tres (03) casos:
Caso I : Cuando la carga axial es pequeña y se permite no tomar en cuenta el factor de
amplificación y cuando la carga axial es apreciable. Es decir:
fa / Fa + fb / Fb ≤ 1 cuando fa / Fa ≤ 0,15
Caso II: Cuando fa / Fa ≥ 0,15 quedaría de la siguiente manera:
fa / Fa + Cm*fb /(1-fa/Fe’)*Fb ≤ 1
donde:
Cm = αm (Norma) = Factor de equivalencia que toma en cuenta las diferentes condicionesde
apoyo y tipos de carga. Para el caso que nos ocupa Flexo – Compresión:
Caso II: Para casos con desplazamiento lateral (pórticos no arriostrados lateralmente):
Cm = αm (Norma) = 0,85 (fijo)](https://image.slidesharecdn.com/elementosaflexocompresion-160516212716/85/Elementos-a-flexo-compresion-13-320.jpg)