3_Deflexión_de_Vigas_Método_Teorema_Área-Momento.pptx

Deflexiones en Vigas
Diseño Dinámico M2003B
F E B R E R O - J U N I O 2 0 2 2
Estudiar diversos métodos para determinar la
deflexión de una viga debido a una carga

» Los teoremas del momento de área utilizan ciertas propiedades
geométricas de la curva elástica para determinar la deflexión y
pendiente de una viga en un punto dado.
» Considere una viga AB sometida a alguna carga arbitraria. Primero, se
dibuja el diagrama que representa la variación de la cantidad M/EI a lo
largo de la viga, que se obtuvo dividiendo el momento flector M entre
la rigidez de flexión EI.
» Excepto por una diferencia en la escala del eje y, este diagrama es el
mismo que el del momento flector si la rigidez a la flexión de la viga es
constante.
2
Teoremasdelmomentodeárea
Teorema del primer momento de área

» Utilizando la ecuación (1) [que se dedujo anteriormente] y recordando
que para rotaciones pequeñas se satisface la ecuación (2),
𝑑2𝑦
𝑑𝑥2 =
𝑀
𝐸𝐼
… (1) ;
𝑑𝑦
𝑑𝑥
= tan𝜃 ≃ 𝜃 … (2)
» podemos plantear la ecuación (3), y esta última despejarla en la
ecuación (4).
𝑑𝜃
𝑑𝑥
=
𝑑2𝑦
𝑑𝑥2 =
𝑀
𝐸𝐼
… (3) ; 𝑑𝜃 =
𝑀
𝐸𝐼
𝑑𝑥 … (4)
» Si consideramos dos puntos arbitrarios C y D en la viga AB y se
integran ambos miembros de la ecuación (4) de C a D, se obtiene la
expresión (5). Donde θC y θD denotan la pendiente en los puntos C y
D.
3
Teorema del primer momento de área
𝜃𝐷 𝐶 = 𝜃𝐷 − 𝜃𝐶 = 𝑥𝐶
𝑥𝐷 𝑀
𝐸𝐼
𝑑𝑥 … (5)

» El miembro del lado derecho de la ecuación (5) representa el área
bajo el diagrama M/EI entre C y D, y el miembro del lado izquierdo
es el ángulo entre las tangentes a la curva elástica en C y D. Este
ángulo esta dado como
𝜃𝐷 𝐶 = área bajo el diagrama
𝑀
𝐸𝐼
entre 𝐶 y 𝐷
» Esta expresión es el teorema del primer momento de área que
permite calcular el ángulo entre las tangentes de la viga en dos
puntos diferentes.
Nota: El área M/EI entre los puntos C y D, localizada por encima del eje x, corresponde a una rotación en
contra de las manecillas del reloj conforme se pasa de C a D. Esto indica que el ángulo θD/C es positivo.
Entonces, un área negativa corresponde a una rotación en sentido horario y, por tanto, el ángulo
correspondiente será negativo.
4
Teorema del primer momento de área 𝜃𝐷 𝐶 = 𝜃𝐷 − 𝜃𝐶 = 𝑥𝐶
𝑥𝐷 𝑀
𝐸𝐼
𝑑𝑥 … (5)

» Considere dos puntos P y P’ localizados entre C y D y a una distancia
dx uno del otro. Las tangentes a la curva elástica dibujadas en P y P'
intersecan un segmento de longitud dt sobre la vertical a través del
punto C. Dado que la pendiente θ en P y el ángulo dθ formado por las
tangentes en P y P' son cantidades pequeñas, se puede suponer que
dt nos arroja la relación (6)
» Al sustituir la ecuación 𝑑𝜃 =
𝑀
𝐸𝐼
𝑑𝑥 … (4) en la relación (6), se obtiene la
expresión (7). Aun considerando los dos puntos arbitrarios C y D en la
viga AB e integrando ambos miembros de la ecuación (7) de C a D, se
obtiene la expresión (8). El miembro del lado izquierdo de la
expresión es igual a la distancia vertical de C a la tangente en D.
Esta distancia se denota por tC/D y se llama desviación tangencial de
C con respecto a D.
5
Teorema del segundo momento de área
𝑑𝑡 = 𝑥1𝑑𝜃 … (6)
𝑑𝑡 = 𝑥1
𝑀
𝐸𝐼
𝑑𝑥 … (7)
𝑡𝐶 𝐷 = 𝑥𝐶
𝑥𝐷
𝑥1
𝑀
𝐸𝐼
𝑑𝑥 … (8)

» Se observa que (M/EI)dx representa un elemento de área bajo el
diagrama (M/EI), y x1(M/EI)dx es el primer momento de ese elemento
con respecto al eje vertical que pasa por C. En este sentido, el
miembro del lado derecho de la ecuación (8) representa el primer
momento del área localizada bajo el diagrama M/EI entre C y D,
con respecto a dicho eje.
𝑡𝐶 𝐷 = área bajo el diagrama
𝑀
𝐸𝐼
entre 𝐶 y 𝐷 ∙ 𝑥1
» Esta expresión es el teorema del segundo momento de área que
permite calcular la distancia vertical desde un punto sobre la viga
hasta la tangente en un segundo punto.
6
Teorema del segundo momento de área 𝑡𝐶 𝐷 = 𝑥𝐶
𝑥𝐷
𝑥1
𝑀
𝐸𝐼
𝑑𝑥 … (8)

Nota: Un punto con una desviación tangencial positiva se localiza por encima de
la tangente correspondiente, mientras que un punto con una desviación
tangencial negativa se localiza debajo de esa tangente.
7
Teorema del segundo momento de área
» Es necesario distinguir entre la desviación
tangencial de C con respecto a D (tC/D) y la
desviación tangencial de D con respecto a C
(tD/C).
• La desviación tangencial tC/D representa la distancia
vertical de C a la tangente a la curva elástica en D, y
se obtiene multiplicando el área bajo el diagrama (M/EI)
por la distancia x1 desde su centroide hasta el eje
vertical que pasa por C.
• La desviación tangencial tD/C representa la distancia
vertical de D a la tangente a la curva elástica en C, y
se obtiene multiplicando el área bajo el diagrama (M/EI)
por la distancia x2 desde su centroide hasta el eje
vertical que pasa por D.
𝑡𝐶 𝐷 = área entre 𝐶 y 𝐷 ∙ 𝑥1 𝑡𝐷 𝐶 = área entre 𝐶 y 𝐷 ∙ 𝑥2

» Los dos teoremas de momento de área se pueden aplicar
eficazmente a la determinación de pendientes y deflexiones solo
si se ha determinado una cierta tangente de referencia a la curva
elástica.
» En el caso de las vigas en voladizo, se conoce la tangente a la
curva elástica en el extremo fijo A y puede usarse como la
tangente de referencia. Es decir, θA = 0, la pendiente de la viga en
cualquier punto D es θD = θD/A y puede obtenerse por medio del
teorema del primer momento de área.
» Por otro lado, la deflexión yD del punto D es igual a la desviación
tangencial tD/A medida desde la tangente de referencia horizontal en A
y puede obtenerse por medio del teorema del segundo momento de
área.
8
Vigasenvoladizoyvigasconcargassimétricas

Vigasenvoladizoyvigasconcargassimétricas
» En el caso de una viga AB simplemente apoyada con una carga simétrica, la tangente en el centro C
de la viga debe ser horizontal (en razón de la simetría) y puede usarse como la tangente de referencia.
» Como θC = 0, la pendiente en el apoyo B es θB = θB/C y puede obtenerse por medio del teorema del primer
momento de área. También se observa que ∣y∣max es igual a la desviación tangencial tB/C y puede obtenerse
por medio del teorema del segundo momento de área. La pendiente en cualquier otro punto de la viga se
encuentra de manera similar. Por ejemplo, en el punto D la deflexión es yD = tD/C – tB/C.
9

» Determine la pendiente y la deflexión en el extremo B de la viga
prismática en voladizo AB cuando está cargada como se indica. Se
sabe que la rigidez a la flexión de la viga es EI = 10 MN-m2.
10
Ejemplo(1)

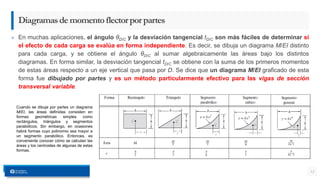
» En muchas aplicaciones, el ángulo θD/C y la desviación tangencial tD/C son más fáciles de determinar si
el efecto de cada carga se evalúa en forma independiente. Es decir, se dibuja un diagrama M/EI distinto
para cada carga, y se obtiene el ángulo θD/C al sumar algebraicamente las áreas bajo los distintos
diagramas. En forma similar, la desviación tangencial tD/C se obtiene con la suma de los primeros momentos
de estas áreas respecto a un eje vertical que pasa por D. Se dice que un diagrama M/EI graficado de esta
forma fue dibujado por partes y es un método particularmente efectivo para las vigas de sección
transversal variable.
12
Diagramasdemomentoflectorporpartes
Cuando se dibuja por partes un diagrama
M/EI, las áreas definidas consisten en
formas geométricas simples como
rectángulos, triángulos y segmentos
parabólicos. Sin embargo, en ocasiones
habrá formas cuyo polinomio sea mayor a
un segmento parabólico. Entonces, es
conveniente conocer cómo se calculan las
áreas y los centroides de algunas de estas
formas.

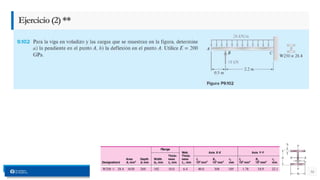
» Determine la pendiente y la deflexión en el extremo B de la viga
prismática. En esta ocasión se sugiere dibujar el diagrama de
momento flector por partos. Por ello, se debe remplazar la carga dada
por dos cargas equivalentes.
13
Ejemplo(2)

» Para la viga prismática AB y la carga que se muestra, determine la
pendiente en el apoyo y la deflexión máxima.
17
Ejemplo(3)

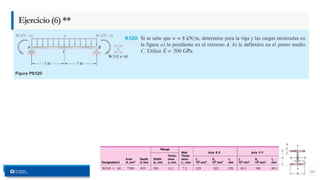
» Las barras prismáticas AD y DB están soldadas entre sí para formar la
viga en voladizo ADB. Si se sabe que la rigidez a la flexión es EI en la
porción AD de la viga, y 2EI en el tramo DB, determine la pendiente y
la deflexión en el extremo A para la carga que se muestra en la figura.
19
Ejemplo(4)

» Cuando una viga saliente o simplemente apoyada soporta una
carga asimétrica, en general no es posible determinar por
inspección el punto de la viga donde la tangente es horizontal. Se
deben emplear otros medios para localizar una tangente de referencia
(es decir, una tangente de pendiente conocida para aplicar cualquiera
de los dos teoremas del momento de área).
» Por lo general resulta conveniente seleccionar la tangente de
referencia en uno de los apoyos de la viga. Por ejemplo, si se
considera la tangente en el apoyo A de la viga simplemente apoyada
AB, su pendiente puede determinarse mediante la expresión (9).
25
Vigasconcargasasimétricas
𝜃𝐴 = −
𝑡𝐵 𝐴
𝐿
… (9)

» Una vez que se ha encontrado la pendiente de la tangente de
referencia, es posible determinar la pendiente θD de la viga en
cualquier punto D mediante el uso del teorema del primer momento de
área para obtener θD/A mediante la ecuación (10).
26
𝜃𝐷 = 𝜃𝐴 + 𝜃𝐷 𝐴 … (10)

» La desviación tangencial tD/A de D con respecto al apoyo A se puede
obtener a partir del teorema del segundo momento de área. Se
observa que tD/A es igual al segmento ED y representa la distancia
vertical desde D hasta la tangente de referencia. Por otro lado, la
deflexión yD del punto D representa la distancia vertical desde D hasta
la línea horizontal AB. Como yD es igual en magnitud al segmento FD,
puede expresarse como la diferencia entre EF y ED. Con esta
información y utilizando los triángulos semejantes AFE y ABH, se
puede obtener la expresión (11) y al recordar las convenciones de
signos usados para las deflexiones y las desviaciones tangenciales, se
obtiene la relación (12)
𝐸𝐹
𝑋
=
𝐻𝐵
𝐿
ó 𝐸𝐹 =
𝑥
𝐿
𝑡𝐵 𝐴 … (11)
𝑦𝐷 = 𝐸𝐷 − 𝐸𝐹 = 𝑡𝐷 𝐴 −
𝑥
𝐿
𝑡𝐵 𝐴 … (12)
27

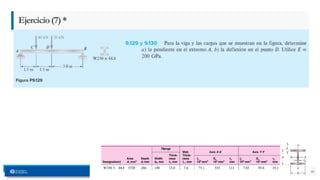
» Para la viga prismática y la carga que se muestran, determine la
pendiente y la deflexión en el punto D.
28
Ejemplo(5)

» Cuando una viga simplemente apoyada o una viga saliente
soporta una carga asimétrica, la deflexión máxima no suele
ocurrir en el centro de la viga.
» Para determinar la deflexión máxima de una viga como la descrita,
primero es necesario localizar el punto K de la viga donde la
tangente es horizontal. La deflexión en ese punto es la deflexión
máxima.
» El análisis debe comenzar con la determinación de una tangente
de referencia en uno de los apoyos. Si se selecciona el apoyo A, la
pendiente θA de la tangente en A se obtiene con el cálculo de la
desviación tangencial tB/A del apoyo B con respecto a A y dividiendo
dicha cantidad entre la distancia L entre los dos apoyos.
32
Vigasconcargasasimétricas(Deflexiónmáxima)

» Como la pendiente θK en el punto K es cero,
θK/A = θK – θA = 0 – θA = –θA
» Si se recuerda el teorema del primer momento de área, el punto K
puede determinarse a partir del diagrama M/EI, al saber que θK/A = –θA
» Al observar que la deflexión máxima |y|max es igual a la desviación
tangencial tA/K del apoyo A con respecto a K, se obtiene |y|max mediante
el cálculo del primer momento del área A entre A y K con respecto al
eje vertical que pasa por A.
33
Vigasconcargasasimétricas(Deflexiónmáxima)

» Determine la deflexión máxima de la viga (continuación del ejemplo 5).
34
Ejemplo(6)

3_Deflexión_de_Vigas_Método_Teorema_Área-Momento.pptx

Más contenido relacionado

Similar a 3_Deflexión_de_Vigas_Método_Teorema_Área-Momento.pptx (20)

Último (20)

3_Deflexión_de_Vigas_Método_Teorema_Área-Momento.pptx